基于改进量子粒子群的切削工艺参数优化

贾伟，赵雪芬

（宁夏大学新华学院，银川 750021）

0 引言

数控技术是利用计算机对机械运动及加工过程进行控制的一种技术。随着数控技术的发展，其在机械加工中发挥着越来越重要的作用。数控加工是一种在数控机床上加工零件的工艺方法，能够实现零件的高效化和自动化加工。在数控加工过程中，选择合理的切削工艺参数不但能够提高加工效率和质量，而且可以降低生产成本。因此，切削工艺参数的选择问题成为数控加工中的重点研究问题。

近年来，随着智能优化算法技术的快速发展，智能优化算法被应用到智能化选择切削工艺参数的研究中，并在切削工艺参数的选择中发挥着重要作用。与其他智能优化算法相比，量子粒子群优化（Quantumbehaved Particle Swarm Optimization，QPSO）算法具有收敛速度快和参数设置较少的优点，使得QPSO算法[1]在切削工艺参数的优化中取得了较好的优化效果[2]。QP⁃SO算法是根据量子力学理论提出的一种具有量子行为的粒子群优化算法。虽然QPSO算法改进了粒子群算法的全局寻优能力，但是它存在易早熟收敛和局部寻优能力较差的问题，为解决该问题，一些学者提出了改进的QPSO算法，例如，Jamalipour等人[3]提出了基于差分进化的QPS算法ODMQPSO，该算法通过差分进化的方式扩大搜索范围。Sun等[4]提出基于高斯分布的QPSO算法GQPSO，该算法通过高斯分布决定局部吸引子的值，以此增强寻优能力。但是这些基于单种群的QPSO算法在种群过大或过小时，会出现计算量大或多样性降低的问题。为解决现有QPSO算法存在的问题和得到更好的切削工艺参数，本文提出一种改进的QPSO算法IQPSO，该算法采用双层多种群寻优策略提高整个种群的全局寻优能力，并将差分进化算法[5]和混沌反向学习[6]应用于顶层和底层各种群的寻优中，从而提高各种群的寻优能力。

1 切削工艺参数数学模型

本文以在数控加工过程中的最大生产率和最低生产成本作为优化目标，在以最大生产率和最低生产成本的切削工艺参数数学模型中[7-10]，完成一道工序的铣销加工的总工时为：

其中，Tw是铣销加工的总工时，Tm是工序的切削时间，Th是由于刀具磨损导致的平均一道工序的换刀时间，Tc是工序之间的换刀时间，Tot是除换刀时间以外的其他辅助时间。

其中，D是刀具直径，L是切削长度，a是切削速度，fz是铣刀每齿进给量，Z是铣刀齿数。

其中，ge是铣削宽度，gp是铣削深度，Cb、m、r、n、d、k、l是铣刀的刀具耐用度系数。

由式（2）和（3）得到的目标函数为：

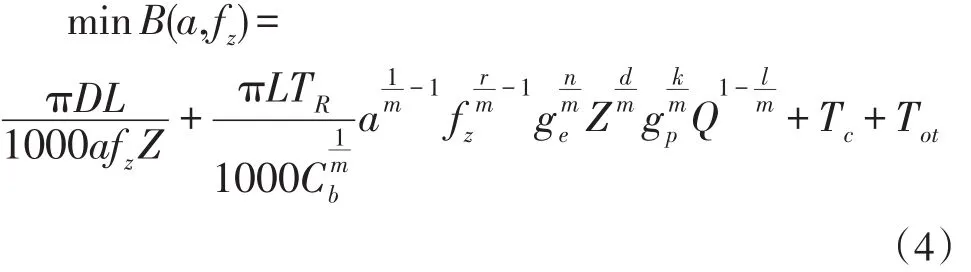
数控机床在加工过程中受到多个方面的约束，切削速度的约束是：

其中，φmin和φmax分别是数控机床主轴的最低和最高转速。

每齿进给量约束是：

切削进给力小于数控机床主轴进给力，则切削力的约束是：

其中，Bfmax是数控机床的最大进给力，φ是主轴转速，xB、yB、dB、lB、wB、KBc是切削力系数。

切削扭矩不能超过主轴最大扭矩，则切削扭矩的约束是：

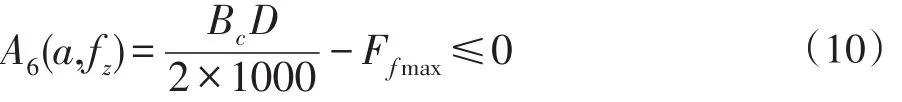
其中，Ffmax是数控机床主轴的最大扭矩。

机械功率小于数控机床的最大有效切削功率，功率约束是：

其中，η是数控机床功率有效系数，Hfmax是数控机床最大有效切削率。

零件加工的表面粗糙度约束是：

其中，σε是刀具的刀尖圆弧半径，Rmax是表面粗糙度的最大值。

2 改进的QPSO算法

假设在一个D维空间中，有一个由M个粒子组成的种群，粒子的位置是Xi(t)=(Xi，1，Xi，2，∙∙∙，Xi，j，∙∙∙，Xi，D)，在QPSO算法中，粒子的运动状态用波函数ψ(x ，t) 描述，通过求解薛定谔方程得到粒子在空间某点出现的概率密度函数，利用蒙特卡洛方法可以得到更新粒子位置的公式：

其中，qi，j(t)是局部吸引子，β是收缩-扩张系数，Cj(t)是所有粒子的个体最优位置的平均最优位置，u是在区间[0 ，1]内均匀分布的随机数。

qi，j(t)由下式计算得到：

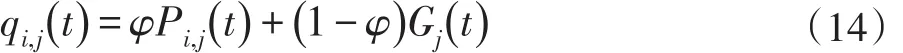
其中，φ是在区间[0 ，1]内均匀分布的随机数，Pi，j(t)是粒子的当前最优位置，Gj(t)是种群的全局最优位置。

Cj(t)由下式计算得到：

其中，M是种群大小。

本文采用的双层多种群策略如图1所示，在底层中，将种群分为F个种群大小为W的子群，每个子群都独立寻找本子群的最优解，然后选取每个子群的最优解Gl1(t)、Gl2(t)、…、GlF(t)进入顶层，形成一个种群jjj大小为F的新种群，在顶层寻找该种群的最优解Gj(t)，在寻找过程中会更新所有顶层粒子的位置，找到顶层种群的最优解Gj(t)后，将顶层每个粒子更新后的位置信息Gjl1(t)、Gjl2(t)、…、GjlF(t)返回到对应的底层子群中，继续引导底层各子群寻找最优解，通过这种策略，可以引导底层的每个子群向全局最优解移动。

图1 双层QPSO算法结构

为了加强单个种群的寻优能力，本文利用差分进化算法和Levy飞行对单个种群进行变异，帮助全局最优解跳出局部最优，增强种群的多样性。差分进化算法是一种智能优化算法，在第t+1次迭代中，对于每一个个体 yi(t)={yi1(t)，yi2(t)，∙∙∙yij(t)}(i∈{1，2，∙∙∙，NP})，变异个体由下式得到：

其中，α1、α2和 α3，是随机正整数，Fˉ是缩放因子。

交叉操作产生的新个体y′i，j(t +1)表示为：

其中，randj是[0 ，1]之间均匀分布的随机数，CR是变异概率，jrand是随机选择指数。

对于混沌反向学习，在文献[6]中使用的Sinusoidal映射的混沌范围具有局限性和均匀分布特性较差的问题[11]，本文采用改进的一维混沌映射Ten-Sine系统[12]：

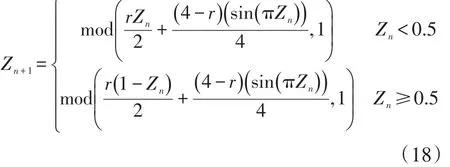
其中，r∈(0 ，4 ]。

在第t次迭代中，对粒子i的反向搜索可由下式计算：

混沌反向学习算法描述如下：

算法1混沌反向学习算法

输入：D是空间维度，最大迭代次数Tmax和种群大小W

输出：初始种群

begin

fori=1toWdo

forj=1toDdo

随机初始化混沌变量Z0j∈(0 ，1) ；

fork=1toTmaxdo

Zk，j=Zk-1，j；//利用式（18）计算混沌映射

end for

xi，j(t)=xmin，j(t)+Zk，j

(xmax，j(t)-xmin，j(t))；

end for

end for

fori=1toWdo

forj=1toDdo

利用式（19）计算第 j维第i个粒子的反向值；

end for

end for

从生成的种群和反向种群中选择最优的W个粒子作为初始种群

end

在QPSO算法中引入差分进化和混沌反向学习后，QPSO算法对于单个种群寻找最优解的描述如下：

算法2对单种群搜索的改进QPSO算法

输入：D是空间维度，最大迭代次数Rmax，种群大小W

输出：全局最优粒子

begin

随机生成种群的初始种群；

fort=1toRmaxdo

利用式（15）计算所有粒子的平均最优位置；

fori=1toWdo

iff(Xi(t))

Pi(t)=Xi(t)；

end if

Gj(t)=min(f (Pi(t) ))；

forj=1toDdo

φ=rand(0，1)；

u=rand(0，1)；

利用式（14）计算 qi，j(t)；

利用式（16）和式（17）对当前种群进行变异，得到新的种群PDE；

利用算法1得到当前种群的方向种群POP；

从当前种群、PDE和POP中选择最优的S个粒子组成新的种群；

end for

end

DQPSO算法在底层和顶层中对多个种群进行寻优，具体的描述如下：

算法3 DQPSO算法

输入：D是空间维度，最大迭代次数Emax，子群数F，子群大小W

输出：全局最优粒子

begin

将当前种群分成F个大小为W的子群；

fore=1toEmaxdo

forf=1toFdo//对于每个子群

调用算法2寻找子群的最优解；

end for

选择所有子群的最优解Gjl1(t)、Gjl2

(t)、…、GjlF(t)作为顶层的粒子，形成新的种群；

调用算法2寻找顶层种群的最优解Gj(t)；

将顶层更新后的粒子Gjl1(t)、Gjl2

(t)、…、GjlF(t)返回到底层；

end for

end

3 实验与分析

在实验中，为了验证改进的QPSO算法在寻优能力和收敛性方面的表现，本文利用改进的QPSO算法IQPSO、QPSO、ODMQPSO和GQPSO分别对切削工艺参数进行优化。实验使用的数控机床是DMG HSC 75Linear，实验中的参数 H=40kW ，φ=4000r/min，afmax=14000mm/min，σε=3.5mm，IQPSO算法的参数为Emax=500，Rmax=300，W=30，Tmax=200。

所有的算法独立运行20次，得到各算法对目标函数优化结果的平均值和标准方差，对各算法的优化结果比较如表1所示，通过表1可以看出，与其他量子粒子群优化算法相比，本文提出的IQPSO算法在搜索全局最优值时能够得到更好的寻优结果。此外，通过标准方差的比较可以看出在所有算法中，IQPSO算法的平均方差最小，这说明IQPSO算法具有最好的稳定性。

表1 各算法的优化平均值和标准方差比较

各算法的收敛性比较如图2所示，从图2的比较结果可以看出，IQPSO算法在迭代次数达到100次左右时已经找到全局最优值，而其他算法需要更多的迭代次数才能找到全局最优值，这说明IQPSO算法的收敛速度较快。从全局最优值来看，只有IQPSO算法在收敛时找到的全局最优值最低，这说明IQPSO算法找到的全局最优值更接近真实的最优值。

图2 各算法的收敛性比较

表1和图2的各算法比较结果说明本文提出的IQPSO具有较好的全局搜索能力和收敛性，这是因为本文采用了双层多种群的寻优策略，利用顶层的最优值引导底层各子群寻优，提高了整个种群的全局寻优能力。此外，本文将差分进化算法和Levy飞行用于顶层和底层各种群的寻优中，加强了各种群的寻优能力，从而提高了局部寻优能力。

4 结语

QPSO算法在优化切削工艺参数中有着重要的应用，针对现有QPSO算法中存在易早熟收敛和局部寻优能力较差的问题，本文提出一种改进的QPSO算法IQPSO，并利用IQPSO对数控机床的切削工艺参数进行优化。在IQPSO算法中使用双层多种群策略，通过差分进化算法和Levy飞行进一步提高顶层和底层中单个种群的寻优能力。实验结果验证了采用本文提出的QPSO具有较好的全局寻优能力和收敛性，能够得到较优的切削工艺参数。