基坑变形组合预测分析及安全性评价
2019-03-11王飞
王 飞
(陕西铁路工程职业技术学院, 陕西 渭南 714099)
0 引言
随着我国城市化建设的快速发展,地下空间的合理利用越来越被重视,基坑工程愈发多见。目前,为充分利用地下空间,基坑工程多以深基坑为主,但限于城市建筑、基础设施等的快速发展,基坑工程施工条件越发困难。在深基坑施工过程中,地质环境的复杂性愈发明显,且深基坑的变形规律难以进行经验借鉴及理论分析,施工过程中的现场监测显得格外重要。为保证基坑工程的顺利施工,需严格控制基坑变形,并加强基坑的变形监测研究,进而预测和分析基坑的安全性[1-3]。
结合工程实际,基坑变形监测数据是基坑安全性的直观表现,对其研究十分必要。国内许多学者也进行了相应研究,如陆培毅等[4]详细分析了基坑不同施工阶段的变形规律,揭示了基坑开挖过程的实际工作状态,为类似工程施工提供了参考依据;黄珏皓等[5]通过对基坑施工过程的详细分析,验证了开挖过程中的时间效应,描述了支护结构的受力特征,对基坑施工提供了理论指导;王兴科等[6]利用支持向量机和神经网络构建基坑变形预测模型,能有效评价基坑变形的稳定性,预测精度能满足工程需要;曹净等[7]利用优化支持向量机构建基坑变形的滚动预测模型,为基坑的动态设计及信息化施工提供了依据。上述研究虽取得了相应的成果,但上述研究方法相对较为单一,也缺少基坑安全性评价研究。本文利用多种预测方法构建基坑变形的组合预测模型,并利用基坑变形控制值构建基坑安全性评价指标,以判断不同阶段基坑变形的安全等级,再利用重标极差法分析基坑安全性的发展趋势,为基坑安全性评价提供一种新的思路。
1 基本原理
1.1 组合预测
组合预测是基于多种单项预测模型,并赋予各单项预测模型相应权值,并根据相应权值对不同单项预测模型进行组合的预测方法。组合预测结果较传统单一预测不一定具有更好的预测精度,但一定具有相对更优的稳定性,能有效减小预测风险。同时,根据组合预测的基本思路,可将其特点归纳如下。
1.1.1 组合预测具有非劣性
各单项预测结果的预测精度具有差异[8],即某单项预测模型的精度会优于另一单项预测模型的精度,但通过组合预测,能有效实现各单项预测模型之间的互补。因此,组合预测精度会优于某一或多个单项预测模型,组合结果具有非劣性。
1.1.2 组合预测存在冗余性
一般情况下,增加单项预测模型的个数,可能一定程度上会改变组合预测模型的关联度,但不一定会增加最大关联度,即可能存在某一单项预测模型的组合权值为0的情况。且当出现该情况时,该单项预测模型被称为冗余方法。
通过上述分析,组合预测结果的精度与单项预测模型息息相关,且单项预测模型间的互补性越强,组合效果越佳。基于文献[9-10]的研究成果,支持向量机SVM(support vector machine)、极限学习机ELM(extreme learning machine)和GM(1,1)模型在基坑变形预测中具有较好的适用性,各单项预测模型的优缺点如表1所示。可以看出,3种预测模型具有较好的互补性。加之三者在基坑变形预测中的适用性和有效性,故将上述3种模型作为组合预测的单项预测模型。
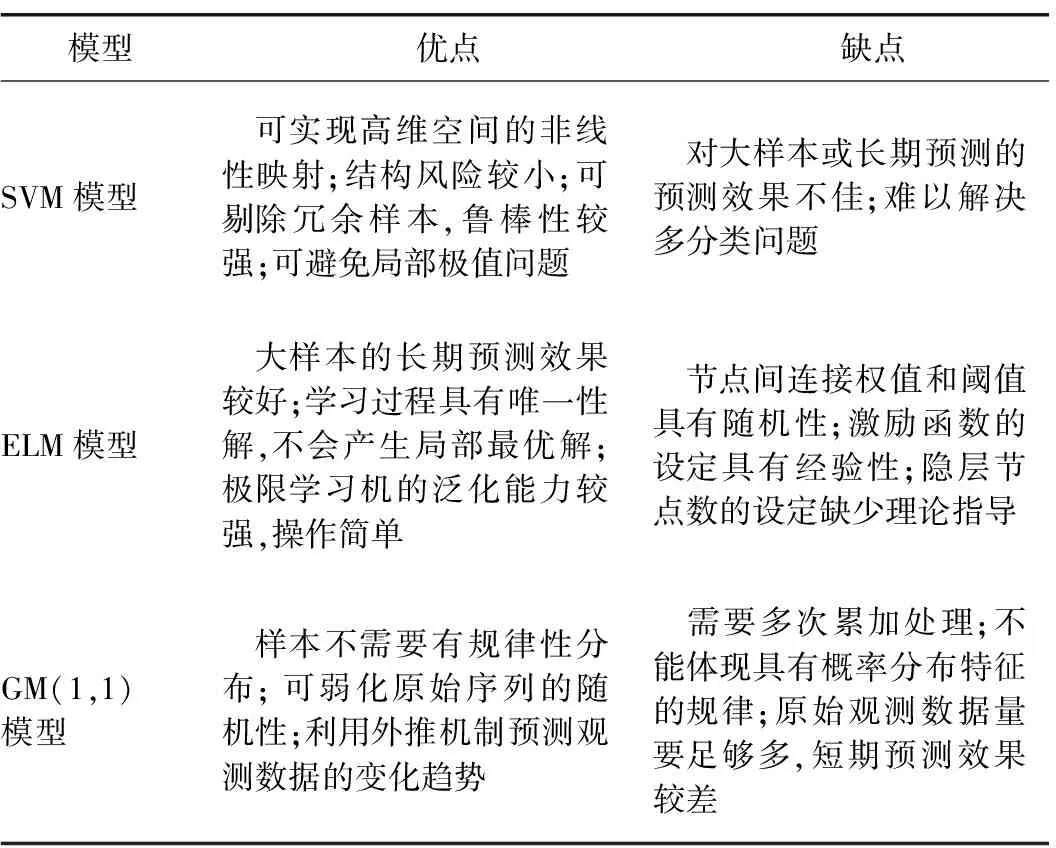
表1 各单项预测模型的优缺点对比表
1.1.3 组合预测基本原理
组合预测权值的确定途径具有多种,大致可分为定权法和非定权法。定权法是指各单项预测模型的组合权值始终为同一非负定值,且权值和为1;非定权法是指各单项预测模型在不同时间节点处的组合权值各不相同,具非线性特征。2种组合方法的基本原理分述如下。
1.1.3.1 定权法
定权法属多目标的规划问题,重点是确定评价指标。结合相关研究成果[11],确定定权法的评价指标为误差和方差,即误差权值法和方差权值法。若将基坑原始变形序列表示为Y={y1,y2,…,yn},根据单项预测,得到第i种预测方法的预测结果Yi={y1i,y2i,…,yni}(n为验证样本长度),且各单项预测模型的组合权值向量P={p1,p2,…,pm},则组合预测结果可表示为:
(1)
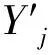
根据上述,再重点对2种定权法的权值求解过程进行详述。误差指的是预测残差的绝对值,方差指的是残差序列的方差值,且两者的值越小,说明单项预测结果越优。
首先,对各单项预测模型的评价指标进行倒数处理,即:
li=1/εi。
(2)
式中:li为第i种单项预测模型的评价指标倒数;εi为第i种单项预测模型的评价指标(误差值或方差值)。
通过对式(2)结果的归一化处理即可得到各单项预测模型的组合权值,如式(3)所示。
(3)
式中pi为第i种预测模型的组合权值。
1.1.3.2 非定权法
非定权法在不同时间节点处的组合权值各有差异,若通过单一计算确定组合权值具有工作量大、操作困难等缺点,故利用BP神经网络和RBF神经网络构建非线性组合预测模型,2种组合方法的实现过程如下: 以各单项预测模型的预测结果作为输入层,并将相应时间节点处的实测值作为输出期望,进而构建出2种神经网络的网络结构。
1.2 安全性评价
通过上述组合预测,虽能很好地判断基坑变形趋势,但却忽视了基坑的安全性,即未对基坑可能发生的危险变形进行研究。同时,基坑施工安全性可通过累计变形量与变形控制值间的相对程度来确定[12]。结合累计变形量及控制变形量,确定了基坑变形的安全性评价指标
(4)
式中:xk为基坑变形控制量(实例控制量为35 mm);xs为评价区间范围内最大变形量;xx为评价区间范围内最小变形量。
根据λ值的计算,可判断基坑变形所处的安全性,即其值越大说明安全性越好,反之安全性越低,并便于对基坑的安全等级进行区分,以便采取相应的安全措施。基坑安全等级区分如表2所示。
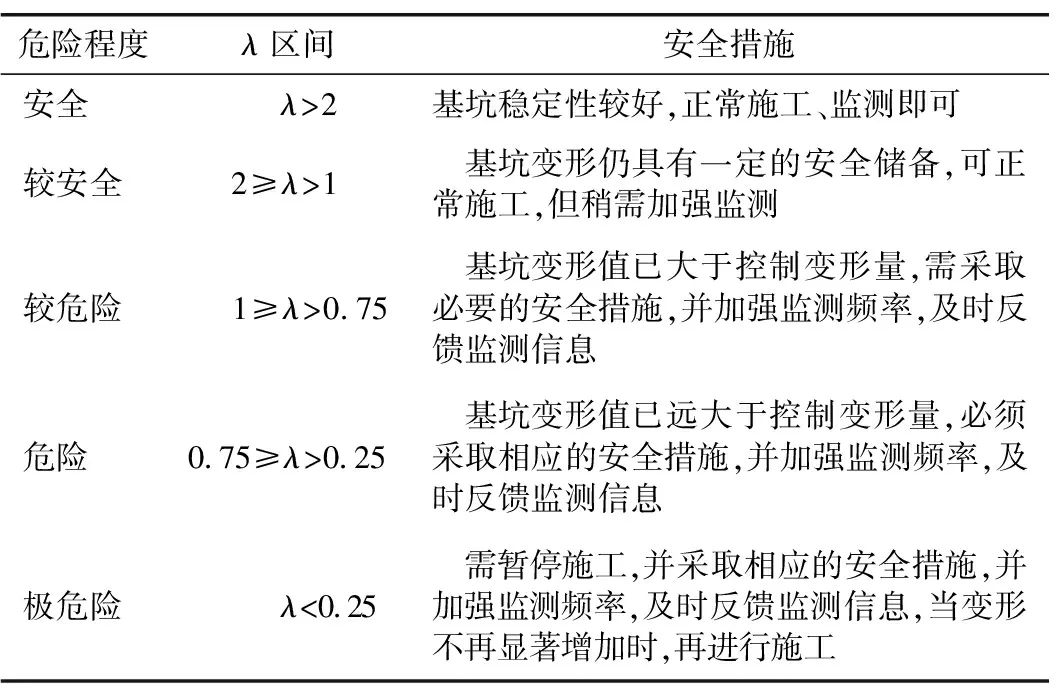
表2 基坑安全等级区分表
上述评价过程仅对某一监测时段的安全性进行评价,并不能对基坑的安全趋势进行评价。为实现基坑安全性的发展趋势判断,且鉴于不同时刻处对应相应的λ值,即可通过计算得到λ值的时间序列,提出利用重标极差法(R/S分析)对λ值序列进行趋势分析,以判断基坑安全性的发展趋势。该方法具有较好的趋势判断能力,其判断依据是根据Hurst指数进行判断,鉴于其基本理论已在文献[13-14]中详述,此处不再赘述,但将安全性趋势判断的依据分述如下。
当Hurst指数在[0,1]之外时,说明重标极差法分析无效;当0 为评价分析序列的相关性,进一步引入CM参数进行评价,其计算公式如式(5)所示。 CM=2(2H-1)-1。 (5) 在评价过程中,CM绝对值越大,说明相关性越强,反之相关性越弱,且CM为正值时,属正相关,反之为负相关。 某基坑长度约为530 m,宽度约为265 m,最大开挖深度约为14.5 m,属深基坑。采用水泥搅拌桩作为止水帷幕,并结合钻孔排桩及预应力锚索作为支护结构。该基坑周边环境复杂,南侧近接住宅楼,最小净距不足50 m,西侧近接变电站,内有办公建筑,属框架结构[15]。鉴于基坑开挖过程具有较大的风险,为避免安全事故的产生,并满足信息化施工的规定,需对基坑进行实时监测,共布设29个沉降监测点,监测点位于基坑周边。其中J20的变形量最大,且连续性较好,将其作为实例验证的数据来源,共计有140个监测周期,监测频率为1次/d,其沉降变形曲线如图1所示。根据施工工况记录,35 d时,完成第1层开挖,施作第1层锚索,当锚索施工完成后,开始第2次土层开挖;105 d时,第2层土层开挖完成,并开始施作第2层锚索;105—140 d时,主要进行第3层土层开挖,且开挖至基坑设计深度14.5 m处。 图1 J20沉降变形曲线 为验证预测模型的有效性,对监测时间进行阶段性划分,共分为3期: 第1期为1—45周期,其中40—45周期为验证样本; 第2期为1—90周期,其中85—90周期为验证样本; 第3期为1—140周期,其中135—140周期为验证样本。同时,为验证组合预测模型的优越性,以第1期为例,详述组合过程对预测精度的影响,得到第1期样本单项预测结果,如表3所示。 表3 第1期单项预测结果统计 由表3可以看出: 1)3种单项预测模型的预测效果具有一定差异,验证了3种单项预测模型的互补性,且SVM模型的最大相对误差为3.89%,最小相对误差为-3.90%,平均相对误差为3.39%; 2)ELM模型的最大相对误差为3.43%,最小相对误差为-2.10%,平均相对误差为2.79%; 3)GM(1,1)模型的最大相对误差为3.76%,最小相对误差为-3.77%,平均相对误差为3.40%; 4)ELM模型的预测精度相对最优,SVM模型与GM(1,1)模型的预测效果相当。 在组合预测中,首先利用误差权值法和方差权值法进行定权组合预测,统计计算得到2种定权法的组合权值为: 根据上述权值,对定权组合预测结果进行计算,结果如表4所示。 表4 第1期定权组合预测结果 由表4可以看出: 1)误差权值法绝对相对误差最大值为3.91%,最小值为1.35%,绝对平均相对误差值为2.14%;方差权值法绝对相对误差最大值为2.15%,最小值为1.25%,绝对平均相对误差值为1.64%。以后者方法预测效果相对更优,具有更好的预测精度及稳定性,得出在定权组合预测中,单项预测模型的稳定性控制能更好地提高预测精度。2)2种定权法的组合预测精度均优于3种单项预测模型,说明定权组合预测能有效提高预测精度,验证了组合预测的有效性。 其次,再利用BP神经网络和RBF神经网络进行非定权组合预测,结果如表5所示。 表5 第1期非定权组合预测结果 由表5可以看出: 1)2种非定权组合预测模型的预测效果较好,均明显优于单项预测模型,再次验证了组合预测模型的优越性。2)RBF神经网络权值法的绝对相对误差均小于2%,平均绝对相对误差为1.06%;BP神经网络权值法的绝对相对误差均小于2%,平均绝对相对误差为0.93%,表明以BP神经网络权值法的组合效果更优。 对比定权组合与非定权组合的预测效果可知,非定权组合预测具有相对更优的组合效果,且以BP神经网络权值法的组合效果最优,故确定组合预测方法为BP神经网络权值法。为进一步验证组合预测模型的普遍适用性,再利用第2、3期数据进行验证,且对141—145周期进行外推预测,以判断基坑变形的发展趋势,结果如表6所示。 表6 第2、3期变形预测结果统计 由表6可以看出: 1)第2期预测结果的绝对相对误差最大为1.73%,绝对平均相对误差为1.17%;第3期预测结果的绝对相对误差最大为1.43%,绝对平均相对误差为1.15%。上述成果表明本文预测模型均具有较好的预测精度,也验证了组合预测思路的普遍适用性。 2)第141—145周期的基坑变形预测值均具有持续增加的特点,说明基坑稳定性及安全性将会进一步减弱,需采取必要措施,以控制基坑变形。 在基坑变形监测过程中,受基坑所处地质条件及施工工艺的影响,基坑变形控制量具有差异,本文实例在结合实际情况及相关规范前提下,确定基坑变形控制量为35 mm。为验证基坑安全性的阶段性特征,根据安全度评价原理,对3个监测阶段的安全性进行评价,结果如表7所示。 表7 基坑安全性阶段性特征统计 由表7可以看出: 随监测时间的持续,基坑的安全性逐渐降低,且第2、3期均处于危险阶段。鉴于该阶段基坑变形值已远大于控制变形量,必须采取相应的安全措施,并加强监测频率,及时反馈监测信息。 基于基坑安全性的λ值时间序列,采用重标极差法分析基坑安全性的发展趋势,且为验证该方法的适用性,也对第1、2期的发展趋势进行分析,并与实测数据进行对比验证。为实现基坑安全性的全面分析,对λ值时间序列的累计序列和速率序列均进行分析,结果如表8所示。 表8 基坑安全性发展趋势分析 由表8可以看出: 1)不同阶段的拟合度均较趋近于1,说明R/S分析过程较好,结果的可信度较高,且累计序列的Hurst指数均大于速率序列,说明累计序列较速率序列的趋势性更强; 2)第1、2期的Hurst指数均大于0.5,说明基坑的安全性将变差,这与后期的变形趋势相符,体现R/S分析在基坑安全性趋势判断中具有适用性; 3)第3期的Hurst指数同样大于0.5,说明基坑的安全性将会进一步减弱,与外推预测结果相符,进一步证明采取安全措施的必要性,并加强监测频率,及时反馈监测信息。 综上所述,变形预测结果与安全性发展趋势分析结果相符,相互佐证了各自分析结果的准确性。 1)单项预测模型难以全面反映基坑的变形规律,而组合预测能有效提高预测精度,并降低预测风险。但在组合预测过程中,鉴于不同单项预测模型具有不同的优点和缺点,需对单项预测模型进行筛选,即单项预测模型间应具有互补性。 2)在组合权值的确定过程中,定权法具有操作简单、使用方便等优点,但其预测精度不及非定权法,且以BP神经网络权值法的组合效果最优。 3)基于基坑变形的安全等级划分,为更为合理判断基坑安全性提供一定的参考。 4)实例分析虽验证了组合预测思路及安全性分析思路的有效性,但对单项预测模型的探讨有限,其他不同单项模型的组合效果仍需进一步研究。且基坑安全性还涉及变形速率等因素,也需进一步探讨基坑安全性的组合判断。2 实例分析
2.1 工程概况

2.2 预测分析
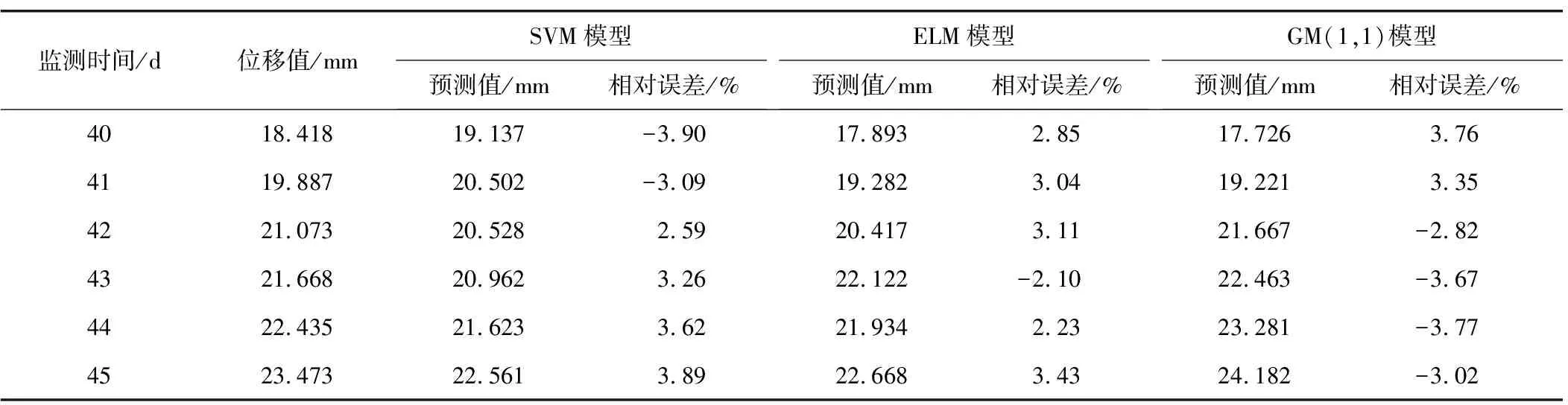


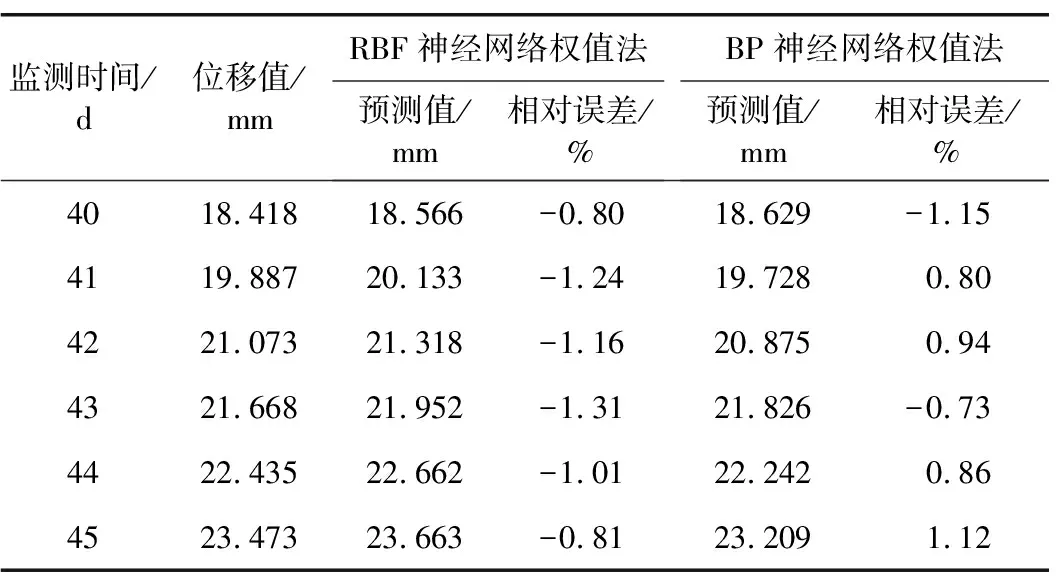
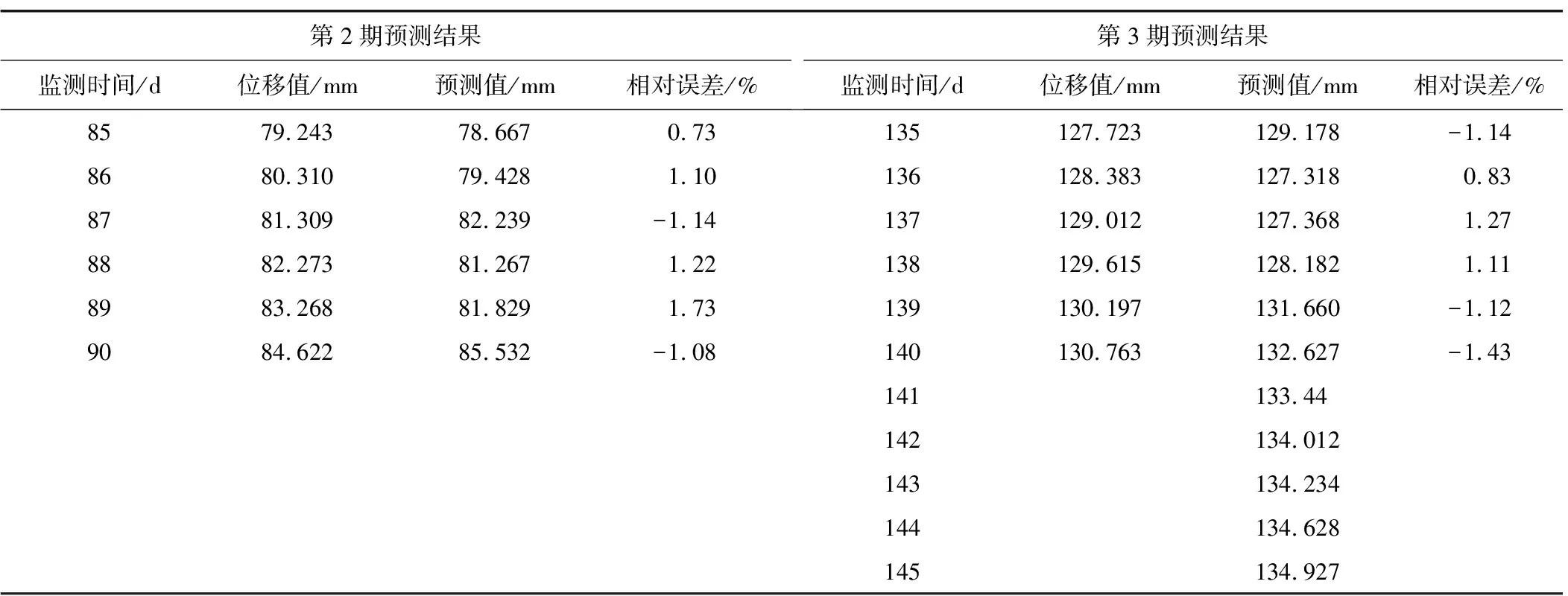
2.3 安全性分析
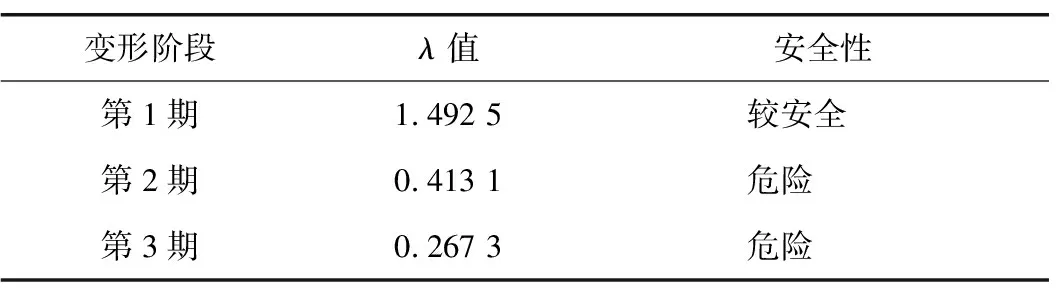
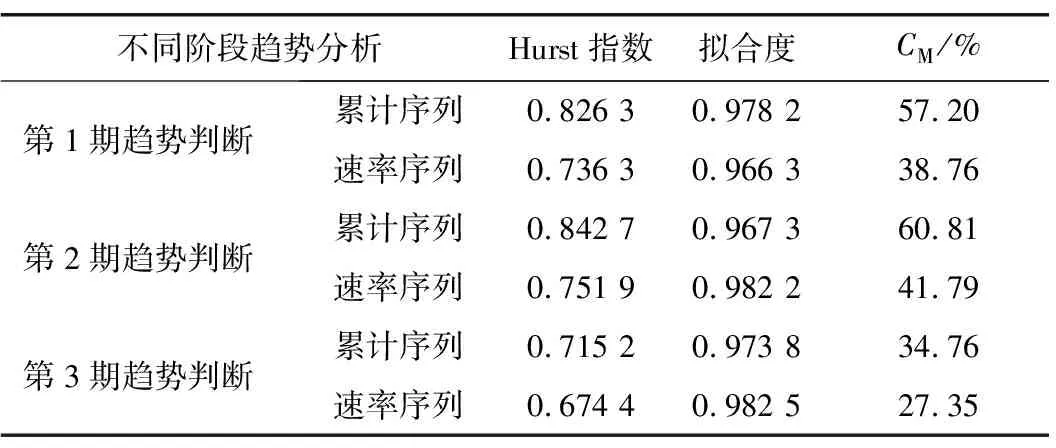
3 结论与讨论
