深水铺管海域涌浪谱峰周期测试技术研究
2019-03-10陈荣旗雷震名孙国民王志勇
陈荣旗,雷震名*,孙国民,王志勇,刘 鹏
(1.海洋石油工程股份有限公司,天津 300451;2.天津大学,天津 300072)
受恶劣海况、复杂地质等环境因素影响,深水海底管道铺设面临施工作业效率低、安全风险高等难题。深水海底管道铺设过程中,由于管道悬链线长度大、铺管船上焊接操作要求高,对铺管船在海洋波流联合作用下的运动响应提出了极高的要求。深水海底管道铺设中长周期涌浪频率低且与深水铺管工程船振动频率接近,易引发结构物与海上涌浪的耦合共振,带来严重的工程风险,甚至引起海上工程事故[1]。
当前的海洋环境预报中,对于风浪、海流的数据较为准确,但对于传播距离长、低频分量占主导、衰减慢的长周期涌浪预报较少,缺乏现场实测数据[2-3]。在我国某海域的深水海洋油气开发中,海底管道铺设长期受到海上涌浪的影响,铺管船长时间在海上待机,铺管作业效率低[4]。研究并克服涌浪对深水铺管作业的影响成为一项亟待攻克的重大难题。
国内外工程界通常采用接触式测波仪进行现场波浪测试。根据原理的不同,接触式测波仪可分为光学、声学、电测学、力学四类;而根据测波仪安装位置,又可分为水面测波仪、水下测波仪两类[5]。近年来,采用非接触式方法[6-7]进行涌浪现场测试,已成为国内外学界及业界研究热点[8-10]。
本文提出了一种基于双目立体视觉原理的海上长周期涌浪谱峰周期现场测试方法,通过进行我国某深水海域铺管现场海上涌浪谱峰周期测试研究,为涌浪谱峰周期监测提供了一种新的方法与借鉴。
1 基于双目立体视觉原理的非接触式测量方法
1.1 双目立体视觉原理
双目立体视觉是基于视差原理,采用摄像机等成像设备,从不同位置获得两幅成像图片,通过仿生学原理、光学三角原理,计算图像对应的位置,从而获取三维信息的方法。基于双目立体视觉原理的测量方法在计算机视觉、工程测算、工业检测、医学成像等领域应用广泛,具有结构简单、效率高、成本低等诸多优点。双目立体视觉主要分为平行式双目立体视觉、交汇式双目立体视觉两类。

图1 平行式双目立体视觉成像原理示意图Fig.1 Principle diagram of parallel binocular stereo vision
平行式双目立体视觉成像原理如图1所示,根据几何关系、以及左右相机图像特征点匹配情况,计算出视差,即可得出该点在三维空间中的坐标。这种方法模型简单,计算方便。
交汇式双目立体视觉成像原理如图2所示,两台摄像机与目标点的连线成一定的角度。根据摄像机的投影映射关系、投影线角度以及几何关系,可确定出目标点的准确位置。投影映射关系、投影线的角度分别由摄像机的内部参数和外部参数来确定。

图2 交汇式双目立体视觉成像原理示意图Fig.2 Principle diagram of convergent binocular stereo vision
1.2 数字图像相关方法
数字图像相关方法是基于视觉技术分析的一种图像测量方法,又称为数字散斑相关法。通过图像处理、识别技术,进行结构物的形状、变形和运动测量。通过采用数字图像相关方法,对同一时刻形成的参照图像和匹配图像进行分析,在参照图像和匹配图像中划定的子区范围内,搜索灰度值相似程度最高的子区,实现特征点匹配,计算出特征点位移和变形量。两块子区的相似程度用相关函数C(P)来定义。相关函数的表达式为
式中:f(x,y)为参照图像灰度分布,g(x,y)为匹配图像灰度分布。如图3所示,(x0,y0)为参照图像中特征点子区的中心坐标,右侧图像为匹配图像子区,方程中‖·‖代表二阶范数运算。上式中x(P) 、y(P)可用位移形函数表示,常用的位移形函数分为零阶、一阶、二阶三种。对函数C(P)取极值,通过计算,可得出x(P),y(P),即来自不同相机的两幅图中相似度最高的子区,可认为是同一点出现在两台相机视野中,在完成相机标定的基础上,可根据求得的位移型函数x(P),y(P),计算出该点的三维坐标。

图3 变形前后参照图像与匹配图像的子区对比Fig.3 Contrast between the reference image sub-area and the matching image subarea after the deformation
1.3 标定方法
利用双目立体视觉原理进行物体的空间位置、形貌测量时,需用到相机内外参数。相机内外参数通过相机标定算法得到。目前,通常使用棋盘格图像进行相机参数标定,标志物的大小尺寸与被测物体的大小比例应保持在一定尺度范围内。采用与被测物尺度相差太大的标志物进行相机标定,标定参数误差较大,易导致实际测量误差大。由于本次测量对象的尺寸较大,不适合利用标定棋盘作为标志物,本文采用监测框架结构做标志物的相机标定方法。
相机标定结果包括内参数和外参数,内参数指的是相机以及镜头的相关参数,而外参数则指的是两个相机之间的相对位置关系。在本文中,相机标定分两步进行,第一步是在实验室内进行内参数标定;第二步是在海上现场根据框架结构实际尺寸进行外参数标定。
1.4 基于傅里叶变换的数字图像处理
在现场涌浪测试过程中,以监测框架结构为标志物,漂浮在水面上的PVC框架结构及相关附属结构随波浪传播而上下起伏,从而为测试提供标尺参照。

图4 棋盘内参数标定结果及监测框架结构现场外参数标定Fig.4 Internal and external parameter calibration
对于采集的图像,不同波面对光的反射及散射情况不同,将所测图像中海域涌浪波面质点的灰度作为变量,该变量随着时间及涌浪传播呈现周期性变化,对现场采集的波浪数据进行滤波除噪,并通过窗函数处理,得到图像的灰度分布。经傅里叶变换处理后,得到瞬时频谱数据,通过时间累计,可得出沿时间进程的频率分布关系。而对图像的频率分布关系进行傅里叶逆变换,则得出图像中的灰度分布关系。
傅里叶频谱图中某一点与邻域点灰度差异的强弱,代表该处梯度的大小,暨频率的大小。其中,低频部分指低梯度的点,高频部分为高梯度点。通过观察傅里叶变换后的频谱图,可以得出图像的能量分布。如果频谱图中暗点数更多,则实际图像较柔和,梯度相对较小;反之,如果频谱图中亮点数多,则实际图像更尖锐,边界分明且灰度差异大。图像经过二维傅里叶变换后,若变换矩阵原点设在中心,其频谱能量集中分布在变换系数矩阵中心附近。若所用的二维傅里叶变换矩阵原点设在左上角,则图像信号能量将集中在系数矩阵的4个角。
2 海上涌浪谱峰周期测试装置及现场测试
2.1 主要测试装置及仪器设备
主要测试装备有高速摄像机、镜头、路由器、高性能计算机等。摄像机是本次测试最重要的仪器设备,其型号为Basler acA2040-25gm GigE,配有 CMOSIS CMV4000 CMOS 感光芯片,400万像素分辨率,主要参数如表1所示。

表1 摄像机的主要参数Tab.1 Main parameters of the camera
本文测试基于双目立体视觉原理,需要两台相机同时工作,采用路由器将两路相机信号合并为一路传入计算机中,采样频率为20 fps以上,对路由器的传输速率要求较高。
同时,为了验证本文基于双目立体视觉原理的非接触式涌浪谱峰周期测试方法及精度,本次测试同步采用浮标同步观测的方法进行数据实测验证。所用的浮标为波浪骑士浮标,有效波高分辨率达0.01 m,波向分辨率1.4°,实测范围0°~360°。
2.2 现场测试
基于以上测试方法,在我国某海域进行长周期涌浪谱峰周期海上现场测试验证。
(1)标志物。
采用的标志物为监测框架结构,长、宽各2 m,采用管直径10 cm的PVC管铰接而成。监测框架结构尾部设置一长5 m的绑扎带,绑扎带上每间隔1 m设置一个橘色浮球。PVC框架结构(包括尾部绑扎带及浮球)作为现场监测的标志物使用。
(2)相机外参数标定。
每一台相机需确定的外参数共有6个,这6个参数具体包括相机光心在大地坐标系中的坐标(记为cx,cy,cz),以及相机的3个坐标轴相对于大地坐标系的三个坐标轴旋转的角度(记为ψ,θ,φ)。本实验中有左右两个相机,共有12个外参数需要确定。
将左、右两台摄像机设置于该海域铺管现场附近某海上固定式钢结构平台生活楼甲板处,通过相机支撑架进行固定。鉴于该固定式钢结构平台的结构形式、尺度及刚度,以及海洋环境条件,平台的细微变形及位移可忽略不计,暨左、右两台摄像机与大地坐标系处于相对静止状态。以平台为参照,通过测量,将左相机坐标系作为大地坐标系,右相机相对于左相机的位置测量结果见表2。

表2 标定参数Tab.2 Calibration parameters
(3)数据采集。
由两架CCD摄像机、传输系统、高性能计算机组成海上涌浪谱峰周期测试系统,在我国某海域进行现场测试,采集频率为0.2 Hz,单次连续测试采集时长100 s。考虑到涌浪方向及海上结构物的绕流影响,全天测试分布在1、2、3、4四个方位进行。各测试点位的位置关系如下,其中左相机坐标系为真实的大地坐标系,平移量为右相机坐标原点相对于左相机坐标原点分别沿x-y-z轴移动的距离,旋转向量为分别绕x-y-z轴旋转的角度。

图5 我国某海域涌浪谱峰周期海上测试Fig.5 Spectrum peak period test of swells in one sea area of China
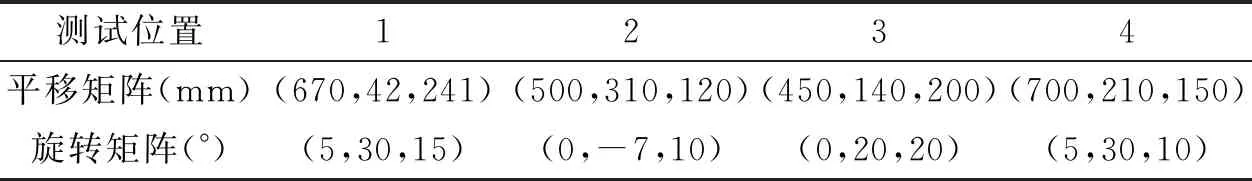
表3 相机外参数样表Tab.3 External parameters sample of camera
通过实时采集数据,并同步采用自编程序进行基于傅里叶变换的数据后处理,实现了测试数据结果的准实时输出,结果输出相较于数据采集延时不超过10 min。
(4)数据处理。
在采集的数据图像中取n个子区(图5),通过采用1.4节的分析方法对子区的平均灰度值随时间、涌浪传播的变化规律进行分析。图6为某子区内部灰度平均值与时间的对应关系,涌浪波面间亮度差异明显,灰度-时间曲线可反映出涌浪的周期性规律,但由于风、风浪及其他因素影响,难以通过灰度-时间曲线直接计算出涌浪周期。通过对“灰度-时间”曲线傅里叶变换可得到“能量-频率”曲线,“能量-频率”曲线中的能量最大值即为涌浪能量,该最大点值对应的频率就是涌浪特征频率,特征频率取倒数即可得到涌浪谱峰周期。

图6 灰度(无量纲)-时间、能量(无量纲)-频率关系Fig.6 Grayscale-Time & Energy-Frequency graph
以上方法可测试出局部区域的涌浪谱峰周期特征值,为了使测试结果更贴近海域实际特征,采用多区域同步检测与多时段检测的措施,经数据处理后,得出精确的海域涌浪谱峰周期测试结果。
3 测试结果
经过在我国某海域的铺管现场海上涌浪谱峰周期的测试,并根据双目立体视觉原理、基于傅里叶变换的数字图像处理技术,分析得到了实测涌浪平均谱峰周期,结果如图7、图8及表4所示。


图7 我国某海域8月18日16:00时涌浪周期实测灰度(无量纲)-时间曲线Fig.7 Test result of Grayscale-Time for swells in the sea-area at 16:00 on August 18th图8 我国某海域8月18日16:00时涌浪周期实测能量(无量纲)-频率曲线Fig.8 Test result of Energy-Frequency for swells in the sea-area at 16:00 on August 18th
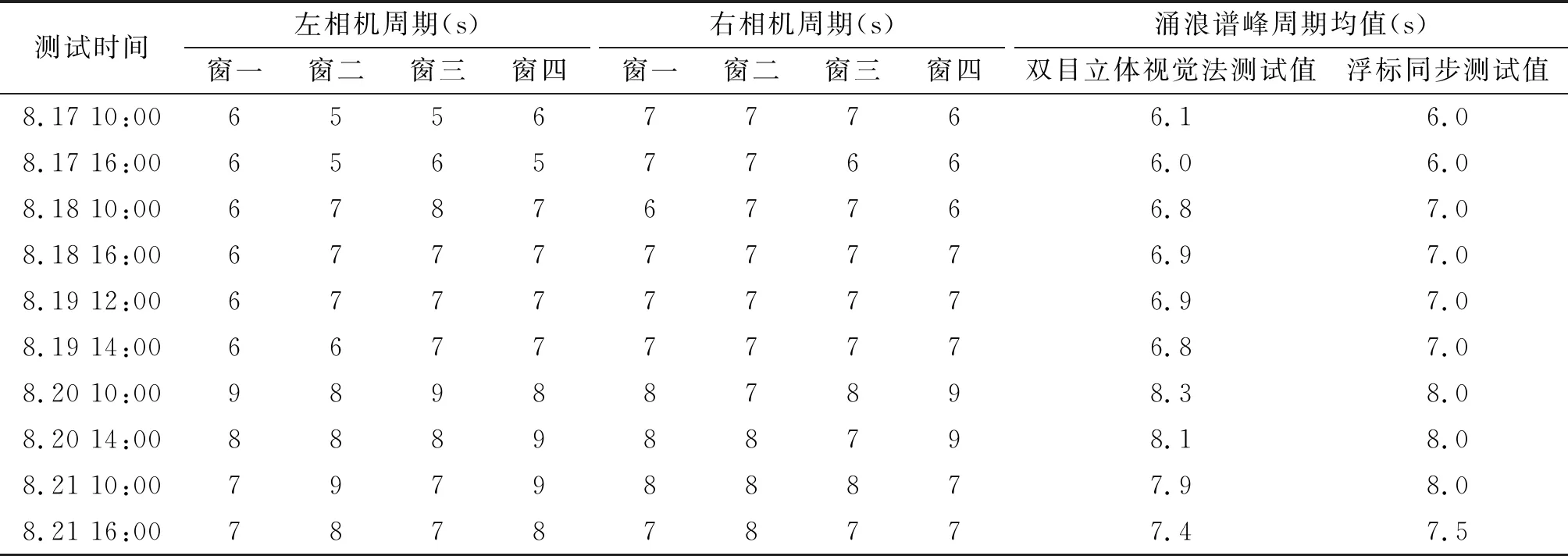
表4 测试结果样表Tab.4 Test results sample
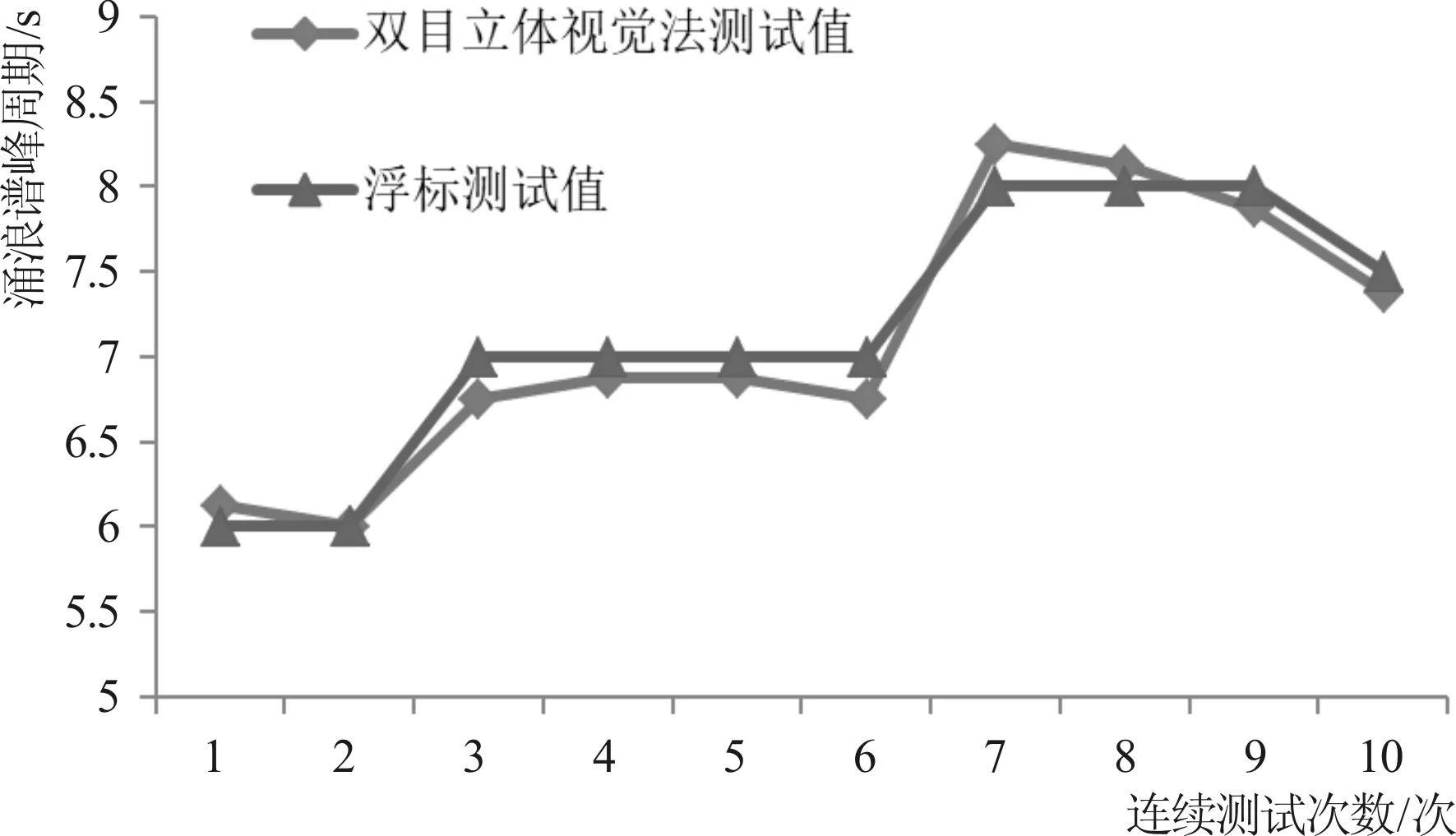
图9 双目立体视觉法测试值与浮标测试值的对比曲线Fig.9 Comparison curve of swells test results between convergent binocular stereo vision method and buoy test method
通过将基于双目立体视觉原理的海上涌浪谱峰周期测试结果与浮标同步测试结果进行对比验证(图9),整体误差率2.07%,两种测试结果一致,得到了相互验证,证明了本文基于双目立体视觉原理的海上涌浪谱峰周期测试方法的正确可行。
4 结论
本文提出了一种基于双目立体视觉原理的海上长周期涌浪谱峰周期现场测试方法,并在我国某深水海域铺管现场,实现了海上涌浪谱峰周期现场测试及验证,为今后深水海底管道海上涌浪监测提供了新的方法与借鉴。
