动水压力作用下堤防边坡流固耦合渗流特性研究

吴 勇，黄江华，左思贤

(1. 浙江华东工程安全技术有限公司，杭州 310014;2. 郑州大学 水利与环境学院，郑州 450001)

堤防边坡的地基土体多为第四纪松散沉积物，堤身填筑土的组成及密实程度都具有非均质性。水流或波浪冲刷作用下堤岸渗流、变形、稳定性研究对堤防的安全运行和管理具有十分重要的意义。

国内外众多学者对波浪冲刷作用进行了大量的研究，主要集中于理论分析和数值计算。在理论分析方面，Sollitt 和Cross[1]利用特征函数法求解得到波浪反射系数和透射系数的解析解；Madsen[2]在假定水头损失与速度为线性的前提下，给出了波浪在堤防土体内的衰减公式；夏艳军[3]等利用方向谱区分不同方向波浪的特点，提出了一种现场实测防波堤波浪透射系数的方法。在数值计算方面，温鸿杰[4]基于改进的SPH方法，模拟研究了规则波在出水堤上的破碎和越浪过程；关大玮[5]基于CFD 软件Flow-3D建立三维数值波浪水槽，模拟研究了规则波和不规则波作用下不可渗光滑斜坡堤的越浪过程；李东洋等[6]基于Open FOAM建立三维数值波浪水槽生成不规则波，研究了正向入射不规则波与扭王块体护面斜坡堤的相互作用；张胡等[7]以线性波浪绕射理论为基础，依据边界元法，建立计算大尺度结构所受波浪力的三维数学模型。

在一定的渗透压力作用下，水流或波浪会使堤防土体的土体颗粒产生动态变形，进而影响体积应变，当前关于水流在堤防饱和土体中的流固耦合渗流特性的研究报道较少。将堤防边坡土体简化为由固体土骨架、水组成的饱和介质，运用土动力理论，构建了动水压力作用下堤防边坡流固耦合渗流动力方程，分析了堤防边坡中的应力、渗流等特性，对于堤防的防治具有一定的指导意义。

1 动水压力作用下的流固耦合动态本构模型

堤防土体的流固耦合渗流规律是一个复杂的动力问题，涉及土力学、流体力学、动力学等诸学科，需要综合考虑堤防土体的运动变形方程、考虑土骨架体积变形的河水渗流方程[8-9]。

1.1 堤防土体的运动变形方程

(1)有效应力原理。

堤防土体属于多孔饱和介质，由土骨架及颗粒间孔隙共同组成。将堤防土体视为弹性介质，固体骨架的有效应力遵循修正的Terzaghi有效应力原理，即

(1)

(2)物理方程。

根据弹性多孔介质的相关理论可知，堤防土体变形的本构方程(即物理方程)

σij=2Gεij+λεvδij

(2)

(3)几何方程。

与常规弹性材料相同，堤防土体固体骨架的几何方程为

(3)

式中：u为堤防土体固体骨架的位移，m。

(4)动力平衡微分方程。

堤防土体固体骨架的位移是空间和时间的参数，即u=u(x,y,z,t)，参照饱和土体的平衡微分方程，给出含堤防土体的平衡微分方程

(4)

式中：w为河水相对于堤防土体固体骨架的位移，m；Fi为应力，Pa；ρ为堤防土体的总密度，kg/m3；ρ=φρs+(1-φ)ρw；ρs为固体土骨架的密度，kg/m3；φ为孔隙率；ρw为流水的密度，kg/m3。

将式(1)和(2)代入式(4)得

(λ+G)uj,ji+Gui,jj+Fi=αpi+ρü+ρw

(5)

根据uj,j=·u、uj,jj=2ui，式(5)可写成矢量的形式

(λ+G)(·u)+G2u+F=αp+ρü+ρw

(6)

1.2 考虑土骨架体积变形的河水渗流方程

(1)孔隙率动态模型。

因此孔隙率是研究河水运移的重要物理参数之一。孔隙率φ随着堤防土体的运动变形而变化，即φ与其所处的应力状态有关，对于等温过程，其计算式如下

(7)

式中：φ0为某一基准温度下且无荷载作用时堤防土体的初始孔隙率；εv为土骨架的体积应变；△p为河水压力变化，Pa，△p=p-p0，p0为河水的初始渗透压力。

(2)渗透率动态模型。

渗透率是反映河水渗流的重要参数指标，常规的河水渗流模型通常将渗透率视为常数，进而忽视了堤防土体骨架变形、孔隙河水压力变化及孔隙体积变化等对渗透率的影响，忽略整个过程中的热效应，根据渗流力学的Krozeny-Carman方程，渗透率k的计算式可简化如下

(8)

式中：k0为某一基准温度下且无荷载作用时堤防土体的初始渗透率，m2。

(3)河水含量计算模型。

将堤坝土体中的河水全部假定为自由水，即

Q=ρwφ

(9)

(4)Darcy渗流定律。

在压力梯度△p作用下，河水在孔隙中作线性渗流运动，该过程遵从Darcy渗流定律，关系式为

(10)

式中：v为河水渗流速度矢量，m/s；η为河水的动力黏度，Pa·s。

(5)河水渗流模型。

煤层河水渗流遵从质量守恒定律，对于单位体积的土体，其渗流方程为

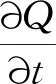
(11)

式中：Q为单位体积堤防土体中的河水含量，kg/m3。

(6)堤防土体总的体积应变。

考虑水压力作用，堤防土体的体积应变εv由两部分组成

(12)

① 固体骨架的变形引起的体积应变，对于二维平面应变问题，由式(3)可得

(13)

② 河水渗流压力增量△p引起的堤防土体的体积应变

(14)

将式(3)和(7)～(10)代入式(11)，经过整理，可得孔隙水渗流方程

(15)

其中，S和Qm的表达式如下

(16)

(17)

(18)

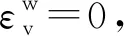
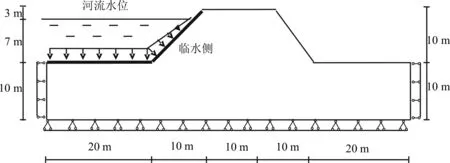
图1 二维计算模型Fig.1 2D computing model

2 数值解答

以某堤防为工程实例，建立二维计算模型，如图1所示，堤防高10 m，河床厚10 m，河水深7 m，两侧边坡1:1放坡，两侧各延伸20 m。

初始和边界条件如下：模型的左右两侧边界施加水平向约束，底边界施加固支约束，其他侧为自由边界；孔隙水压力p0=γwh(h为河水的压力水头)。

表1 物理力学参数Tab.1 Physical mechanics parameters

图2 二维网格划分模型Fig.2 Two-dimensional meshing model

假定堤防土体为均质的各向同性介质，堤防土体和河水的物理力学参数见表1。

运用COMSOL软件，对流固耦合动力方程进行数据求解，二维网格划分如图2所示。

首先采用模型I，通过数值计算，得到了孔隙水压力云图、水平渗流速度云图、竖向渗流速度云图，如图3所示。

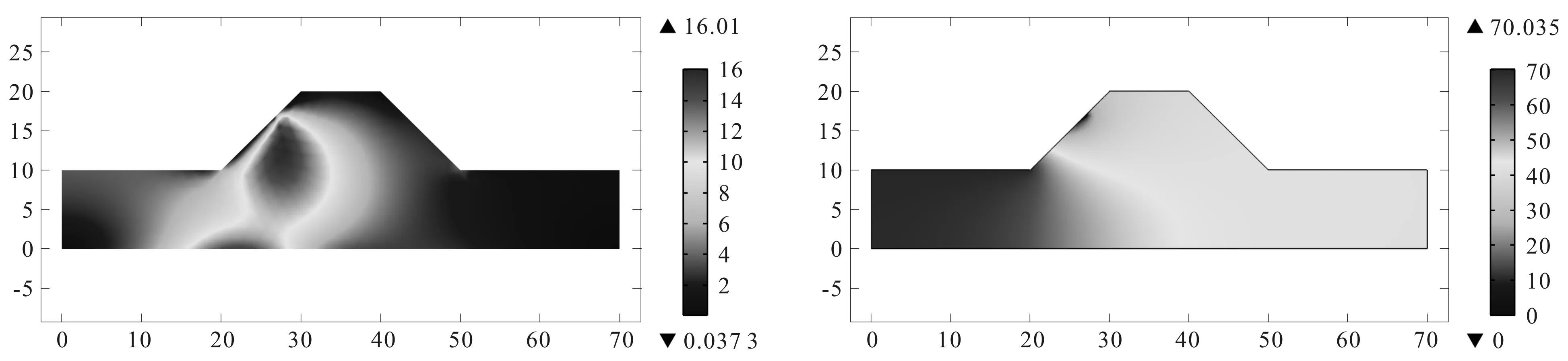
3-a Mises应力云图(MPa)3-b 孔隙水压力云图(Pa)

3-c 水平渗流速度云图(mm/s)3-d 竖向渗流速度云图(mm/s)图3 模型I的计算结果图Fig.3 Simulated results of model I

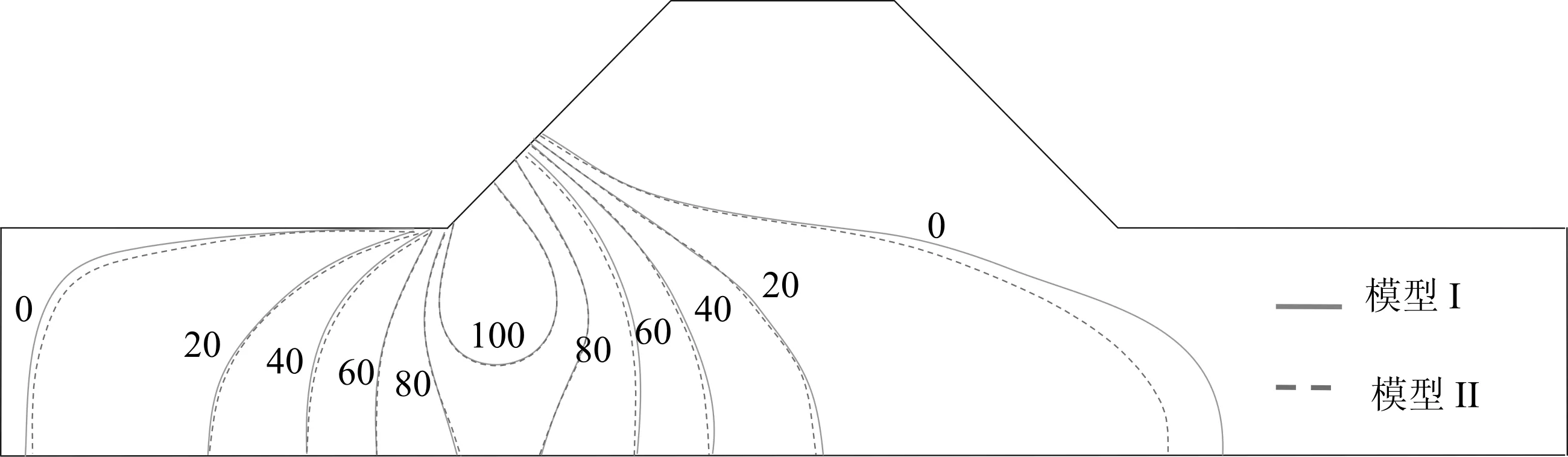
图4 水平渗流速度等值线的对比图(单位：mm/s)Fig.4 Comparison of horizontal seepage velocity contours

从图3-a可以看出，河水的渗流能够引起堤防边坡土体较明显的应力变化，河水表面与堤防土体的交界面处出现较大的应力集中，因此堤防边坡在水土界面处添加防冲刷层是非常必要的保护措施；从图3-b可以看出，河床土体的孔隙水压力高于堤防边坡，这与实际情况相符；从图3-c和3-d可以看出，水平渗流和竖向渗流主要发生在堤防边坡水土界面处的一定区域内，由于水头压力较小，在堤防边坡远处的区域内，渗流速度变缓并最终趋于零。

采用模型II，不考虑河水渗流压力引起土颗粒位移而造成土骨架的体积变形，以水平渗流速度为例，对比了模型I的模型II的计算结果差异，如图4所示。

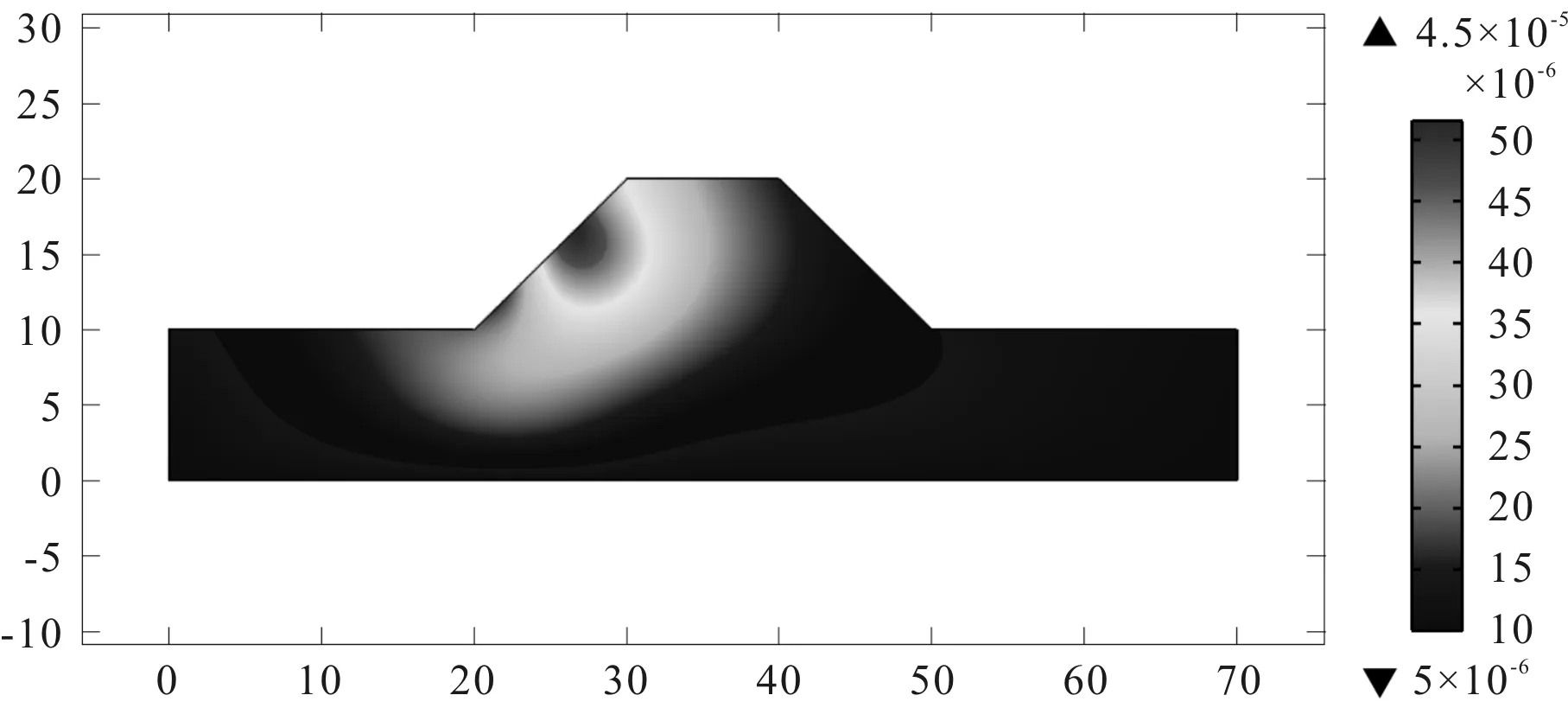
图5 渗流作用下的堤防沉降(单位：m)Fig.5 Embankment settlement under seepage

从图4可以看出，相较于模型II，模型I(考虑流体压力引起土骨架压缩而引起的总体积应变的增大)的渗流影响区域较远，在河水渗流动压力的作用下，固体土骨架的压缩变形增大，土的孔隙率提高，流水的渗流路径较远，因此在堤防边坡防护设计时，应充分考虑水头、水流速度等引起土体的动位移。

采用模型I，进一步得到了动水压力作用下堤防边坡的沉降云图，如图5所示。

由图5所示，堤防边坡的沉降主要发生在临水边坡一侧，而渗流作用下的边坡沉降较小，最大值仅为0.045 mm，可以忽略不计，结合文献[1-7]的相关研究结果，水流动水压力引起的冲刷变形是造成边坡失稳的最主要外因。

3 结论

在外部压力作用下，土骨架整体会发生压缩变形，孔隙率降低；孔隙水渗流过程引起的拖曳力(即动水压力)属于土体内力，动水压力差会造成土颗粒自身的压缩，进而引起整体土骨架孔隙率的增大。考虑动水压力引起的土骨架总体积应变、堤防边坡土体的孔隙率和渗透率受渗流影响的变量，运用饱和土力学和流体力学理论构建了饱和土体的运动方程和Darcy渗流方程，运用COMSOL软件分析了动水压力作用下堤防边坡的流固耦合特性，研究结果表明：(1)模型Ⅰ(充分考虑孔隙水渗流压力引起的体积变形)比模型Ⅱ(不考虑孔隙水渗流压力引起的体积变形)更符合实际情况，动水压力会引起固体土骨架的压缩变形，土的孔隙率提高，流水的渗流路径较远，而这种趋势随着高动能水流冲刷力增大而提高；(2)堤防边坡的沉降主要发生在临水边坡一侧，渗流作用引起的边坡沉降较小，最大值仅为0.045 mm，可以忽略不计。