基于求解双侧对流条件Stefan问题的高炉炉缸凝壳生成过程数学模型

2019-03-08，，

材料与冶金学报 2019年1期

，，

(1 宝山钢铁股份有限公司，上海201901，2 东北大学冶金学院，沈阳110819)

现阶段常用于砌筑高炉炉缸的石墨质和陶瓷质耐火材料均无法长期抵御炙热渣铁的侵损[1-4].事实上，在保温性好、抗化学侵蚀和机械破坏等性能优异的超级耐火材料问世前，高炉炉缸内衬在生产过程中的耗损不可避免.目前来看，采用较高导热能力的衬材，配备高效冷却器，以炉缸内熔融产物为原料，在衬材热面形成“自保护”的凝壳(文献中常使用诸如凝铁层、渣铁锅、沉积层等相近术语)，是将内衬与高温渣铁隔绝，从而保障炉缸长期安全的根本途径.

从传热角度来说，高炉炉缸凝壳的生成是衬材热面铁水熔池的对流供热、铁水显热以及潜热被其冷面冷却器中流动介质不断带出的动态过程.冷却制度一定时，随着凝壳增厚，整个传热体系的热阻逐渐增大，使得凝壳最终稳定在一平衡厚度.鉴于冷却器的工作原理同为对流换热，高炉炉缸凝壳的生成可视为计算域两端均为对流条件的凝固传热问题.这类双侧对流条件的移动边界问题亦属Stefan问题的范畴，其理论解算一般很复杂，至今仍是应用数学领域的研究热点之一.钢铁冶金领域的模铸和连铸过程涉及类似问题，一些学者从理论上推导了不同传热控制环节下的解析解，从而可以绘制熔体凝固层厚度随时间的变化曲线[5-6].必须指出的是，与炉缸凝壳生成过程不同，模铸和连铸的Stefan问题通常不考虑边界上的对流换热.更重要的是，模铸和连铸的衬材与高炉炉缸相比，无论是在影响热量传输的壁面厚度还是其热物性参数方面，均存在显著差别.由此可以推断，模铸或连铸的Stefan问题解析解不适用于描述高炉炉缸凝壳的生成过程.到目前为止，国内外关于凝壳生成动态过程的系统研究还未见报导.绝大多数学者趋于借助多层平壁的一维稳态传热模型，分析多样化因素对凝壳平衡厚度的影响[7-9].然而，若想更进一步探究凝壳生成的动态，即非稳态过程，仍需设法求解上述双侧对流条件的Stefan问题.这些便是本文研究的背景和主要目的.

基于求解上述双侧对流条件的Stefan问题，本文结合理论分析和数值计算方法，建立能够准确描述高炉炉缸内衬热面凝壳生成过程的数值传热模型.在重点阐述此模型构建思路的同时，本文还进行相应准稳态模型的推导.最后，借助相应条件下的实验测量值校验这两种模型计算结果的精确度，并开展模型适用性的相关讨论.

1 模型构建

1.1 主要假设与简化

鉴于高炉炉缸内传输现象的复杂性及其影响因素的多样和多变，为建立凝壳生成过程的数学模型，进行以下假设与简化.

(1)暂不考虑高炉炉缸的实际几何形状.鉴于高炉(圆筒形)炉缸的曲率半径极大，将凝壳的生成简化为通过多层平壁的一维非稳态传热过程，其中各层材料的密度、热容以及导热系数为常数.

(2)暂不考虑凝壳生成所涉及的传质现象，并假定铁水的固相线为1 423 K.将铁水流动、液相线下糊状区、热辐射、焦炭以及铁水显热等因素的影响归结为一熔池综合对流换热系数.

(3)将炉缸侧壁内的冷却壁或炉底水冷盘管做一维等效处理，并视其为对流边界.将水温、水、垢层以及冷却器壁面条件等因素的影响归结速为一冷却水综合对流换热系数.

1.2 控制方程

为提高模型的通用性，模型构建时考虑的多层平壁由n层耐材砖衬和1层凝壳构成，如图1所示.与传统的多层平壁一维非稳态传热体系不同，图1所示体系第n+1层，即凝壳层的厚度随时间变化，导致计算区域不定.

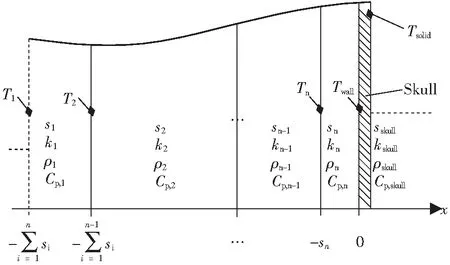
图1 多层平壁一维非稳态传热体系示意图Fig.1 A sketch of one-dimensional heat transfer through a composite plane wall

结合图1，可在各层材料的厚度范围内写出如下传热控制方程.

(1)

式中，T为温度(K)，t为时间(s).ρ、Cp以及k为各层材料的密度(kg/m3)、比热容J/(kg·K)以及导热系数W/(m·K).

qcold=hcold(T1-Tcold)

(2)

式中，q为热通量(W/m2)，h为综合对流换热系数W/(m2·K)，下标cold和1分别代表冷却水和第1层平壁(即与冷却壁紧邻的耐材)的冷面，也就是整个传热体系的冷面位置.

图1所示传热体系热面，即x=sskull处的热量平衡为

(3)

式中，L为凝固潜热J/(kg·K)，下标skull、hot和solid分别代表凝壳、熔池以及熔体固相线.

记凝壳与耐材砖衬界面，即x=0处的温度为Twall，则相应位置两侧的热通量遵循

(4)

1.3 算法设计与计算流程

针对厚度变化的凝壳层，可应用变量置换法推导其一维非稳态传热方程的解[10]，即

(5)

式中，a为凝壳的热扩散系数(m2/s)，U为一未知温度，在以下算法设计中可以消去.

由式(5)可得x=sskull处的温度表达式，为

(6)

由式(5)亦可得凝壳层两端的温度梯度分别为：

(7)

(8)

由式(7)和式(8)可得

(9)

至此，联立式(3)、式(4)和式(9)可得

(10)

而联立式(4)、式(6)和式(7)可得

(11)

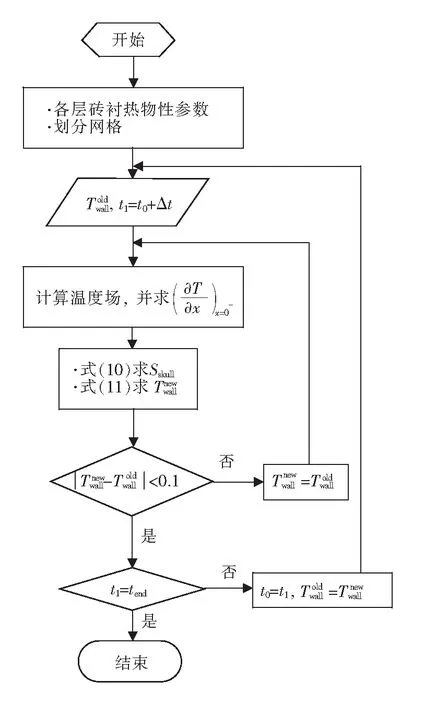
图2 高炉炉缸凝壳生成过程数值传热模型计算流程图Fig.2 The flow chart of the numerical heat transfer model of skull buildup process for a blast furnace hearth

1.4 准稳态模型

针对图1所示的传热体系，亦可在准稳态假设的前提下写出如下热量平衡方程

(12)

将式(12)分离变量可得

(13)

积分式(13)可得

(14)

式(14)中y的取值需满足

(15)

2 结果分析及讨论

本文通过NASA技术报告[11]中的实验测量值对以上两种数学模型的精确度进行校验.若暂不考虑高炉炉缸凝壳生成过程中的传质行为，该技术报告所述实验现象与炉缸凝壳的生成同为双侧对流条件的Stefan问题，具体涉及一定厚度铬镍铁合金(inconel)双侧对流条件下水的凝固过程.

图3为上述两种模型计算结果与相应实验测量值的比较，其中各算例的主要计算参数见图中实验条件.相关初始条件和材料的热物性参数详见文献[11].另外，数值传热模型中采用有限元法编制程序进行inconel平壁内非稳态传热的计算，并根据前期的参数敏感度分析，设定时间步长Δt为1 s.

图3 数值传热模型和准稳态模型计算结果与相应实验测量值的比较Fig.3 Results from the numerical heat transfer model and quasi-steady state model with the corresponding experimental data

由图3可知，从实验测量凝壳厚度随时间的变化上看，数值传热模型预测结果的精确度高于准稳态模型.具体来说，较数值传热模型，准稳态模型计算的凝壳增长速率更大.也就是说，在同一时刻，准稳态模型对应传热体系的热阻更大，带来的结果是其预测的界面温度更低，传热体系达到平衡所需的时间更短，正如图3中的虚线和实线末端对应时刻所示.

图3的对比结果表明，应用准稳态模型解析inconel平壁双侧对流条件Stefan问题存在一定误差.这实际上决定于准稳态假设自身，其可简述为凝壳的增长速率远小于凝壳变化导致的温度扰动于各层平壁中的传播速率.也就是说，单位厚度凝壳生成的时间段内，各层平壁中的温度分布已达稳定状态.对于一维平壁而言，若导热系数为常数，稳态传热条件下的温度分布是斜率为热阻的直线.图4为不同时刻数值传热模型所得inconel平壁内温度分布与稳态传热对应结果的比较.由图可知，即使对于热扩散系数较大(3.98×10-6m2/s)且厚度(温度扰动传播距离)仅为4.67 mm的inconel平壁而言，其温度分布在凝壳生成初期也未达到稳定状态.相应时刻数值传热模型所得凝壳层内温度分布与稳态传热对应结果的比较与图4所示趋势类似，在此不再赘述.据此可以推断，若考虑热扩散系数更小但厚度远大于4.67 mm的高炉炉缸衬材，准稳态模型的计算误差将成倍增大.

图4 数值传热模型计算inconel平壁内温度分布与稳态传热对应结果的比较Fig.4 Temperature distributions in inconel plane calculated by the numerical heat transfer model and by the steady-state model

为进一步展示本文数值传热模型的可用性，以典型陶瓷杯结构炉缸为例，研究陶瓷杯壁厚度对炉缸热面凝壳生成过程的影响.模型考虑两层总厚为0.5 m的耐材砖衬，其中第1层为微孔炭砖，第2层为陶瓷杯壁.参考相关文献[1, 3, 4, 7-9]，本文模型的计算参数设定为：微孔炭砖密度、热容和导热系数分别为1 600 kg/m3、2 000 J/(kg·K)和20 W/(m·K)；陶瓷杯壁密度、热容和导热系数分别为2 500 kg/m3、1 100 J/(kg·K)和2.5 W/(m·K)；铁水凝壳的密度、热容、导热系数和凝固潜热分别为3 000 kg/m3、950 J/(kg·K)、2 W/(m·K)和2.3×105J/(kg·K)；熔池温度和其综合对流换热系数为1 773 K和50 W/(m2·K)；冷却水温度及其综合对流换热系数分别为298 K和1 000 W/(m2·K).此外，为提高各算例结果的可比性，计算的终止条件为凝壳厚度达到相应平衡厚度的95%，且微孔炭砖和陶瓷杯壁内的初始温度均设定为铁水固相线.可以预测，在计算开始后的一段时间内，陶瓷杯壁热面的传热条件无法维持凝壳生成所需的热通量，也就没有凝壳生成.因此，下文各图中的零时刻与计算的起始时刻不相对应，而是指陶瓷杯壁热面刚刚出现凝壳之际.

图5为陶瓷杯壁厚度对高炉炉缸凝壳生成过程的影响.总的来说，炉墙总厚不变时，陶瓷杯壁越薄(即图中sn越小)，炉墙热面的凝壳越厚.与之相应的是，达到传热平衡所需的时间越长.陶瓷杯壁在炉墙中所占比例由16%降低到4%时，炉墙热面凝壳厚度增加2倍以上.这表明，炉役初期陶瓷杯壁基本完整时，高炉炉缸热面不易形成凝壳.但随着“他保护”陶瓷杯壁的不断侵损减薄，炉墙传热体系热阻降低，炉缸会逐渐转入利用当地铁水生产凝壳的低成本“自保护”模式.据此可以推断，在保障冷却强度和稳定出铁操作的前提下，陶瓷杯壁越薄，炉缸越早转入“自保护”模式.

图5 陶瓷杯壁厚度对高炉炉缸凝壳生成过程的影响Fig.5 Influence of the ceramic cup sidewall thickness on the skull buildup process of a blast furnace hearth

图6为陶瓷杯壁厚度对炭砖热面温度的影响.由图可知，一个凝壳生成周期内，炭砖的热面温度逐渐降低，并最终趋于稳定.炉墙总厚不变时，陶瓷杯壁越薄，炭砖热面温度越高，且变化幅度越大.陶瓷杯壁在炉墙中所占比例由16%降低到4%时，凝壳生成前期炭砖热面的温降速率急剧提高，会加剧炭砖的热震.因此，炉役中后期陶瓷杯损耗殆尽后，在实际生产中须重视炉缸区域的监测，一旦出现凝壳消熔的迹象，应及时调整，保证新的凝壳生成周期开始时炭砖热面仍附着有一定比例的凝壳(“自生”陶瓷杯)，借以降低热震导致的炭砖耗损.式(3)中hhot为炉缸铁水综合对流换热系数，目前还未出现相关的系统研究和实验测定.根据定义，此对流换热系数与炉缸铁水的排放和死料柱行为密切相关.因此，实际生产中若出现凝壳消熔、炉缸壁面温度走高的迹象，通过减小上述对流换热系数，保证凝壳厚度的技术措施包括：①退产量，降低炉缸铁水流速；②延长铁口，迫使铁水向炉芯流动，降低壁面流速；③改善炉缸死料柱透液性，控制环流，降低壁面流速.