采用改进神经网络PID控制的移动机器人轨迹追踪控制研究

李 蕾，刘建鹏



采用改进神经网络PID控制的移动机器人轨迹追踪控制研究

*李 蕾1，刘建鹏2

（1.安徽三联学院机械工程学院，安徽，合肥 230601；2.安徽四创电子股份有限公司气象探测系统事业部，安徽，合肥 230000）

为了提高双轮移动机器人运动轨迹追踪精度，采用改进粒子群算法优化BP神经网络PID控制器，并对控制效果进行仿真验证。创建双轮移动机器人模型简图，给出运动轨迹误差方程式。在传统PID控制基础上增加BP神经网络结构，引用粒子群算法并对其进行改进，采用改进粒子群算法优化BP神经网络PID控制调整参数，给出双轮移动机器人PID控制参数优化流程。采用数学软件MATLAB对双轮移动机器人轨迹追踪误差进行仿真验证，并与传统PID控制追踪误差进行对比。仿真曲线显示：在理想环境中，双轮移动机器人采用两种控制方法都能较好地实现轨迹追踪，追踪误差较小；在干扰波形环境中，传统PID控制双轮移动机器人追踪误差较大，而改进PID控制双轮移动机器人追踪误差较小。采用改进粒子群算法优化BP神经网络PID控制器，可以提高移动机器人运动轨迹追踪精度。

PID控制；BP神经网络结构；改进粒子群算法；追踪误差

0 引言

机器人的诞生带动了自动化产业，促进了工业的快速发展，是现代最伟大的科技成果之一。机器人可以代替人类手工劳动，提高生产效率。由于固定机器人还不能满足社会发展的需要，从而诞生了移动机器人。移动机器人运动相对灵活，在焊接、建筑、采矿、排险及航空领域得到了广泛的应用[1]。移动机器人具有多种不确定因素，对移动机器人综合性能要求更高。为了能够实现更短路径、更精确的目标追踪[2]，移动机器人必须具有优良的导航系统，更稳定的控制系统，研究抗干扰移动机器人，对于促进机器人发展具有重要的意义。

移动机器人运动的稳定性受到许多学者的关注，为了提高移动机器人的稳定性，学者对其进行了研究。例如：文献[3]研究移动机器人模糊控制方法，建立了移动机器人动力学模型，引入模糊理论，设计了移动机器人轨迹模糊辨识控制算法，通过MATLAB软件对移动机器人跟踪轨迹进行仿真，提高了移动机器人轨迹跟踪精度；文献[4]研究了移动机器人位置式PID控制方法，创建两轮移动机器人运动模型，通过坐标系推导出轨迹运动姿态方程式，对传统PID控制进行改进，设计出位置式PID控制算法，采用MATLAB软件对机器人轨迹跟踪误差进行仿真，提高了移动机器人轨迹跟踪的稳定性；文献[5]研究了移动机器人滑模控制方法，建立移动机器人与路径运动方程式，设计了滑模控制器，采用李雅普诺夫函数对运动的稳定性进行证明，通过MATLAB软件对移动机器人运动轨迹跟踪进行仿真，从而减弱了输出系统的抖动现象。

移动机器人在干扰环境中执行任务时，运动轨迹追踪误差较大，不能执行机器人高精度的定位。对此，本文以双轮移动机器人为例，建立其模型简图，给出机器人动力学方程式。采用修正粒子群算法优化BP神经网络PID控制器。在干扰波形环境中对优化后的PID控制器进行检验，并与传统PID控制误差进行比较和分析，为深入研究双轮移动机器人轨迹追踪控制方法提供理论依据。

1 双轮移动机器人

双轮移动机器人如图1所示，点为目标位置运动圆心，点为机器人当前位置，为机器人运动速度，为机器人角速度，为当前位置与目标位置之间的距离，为角偏差。

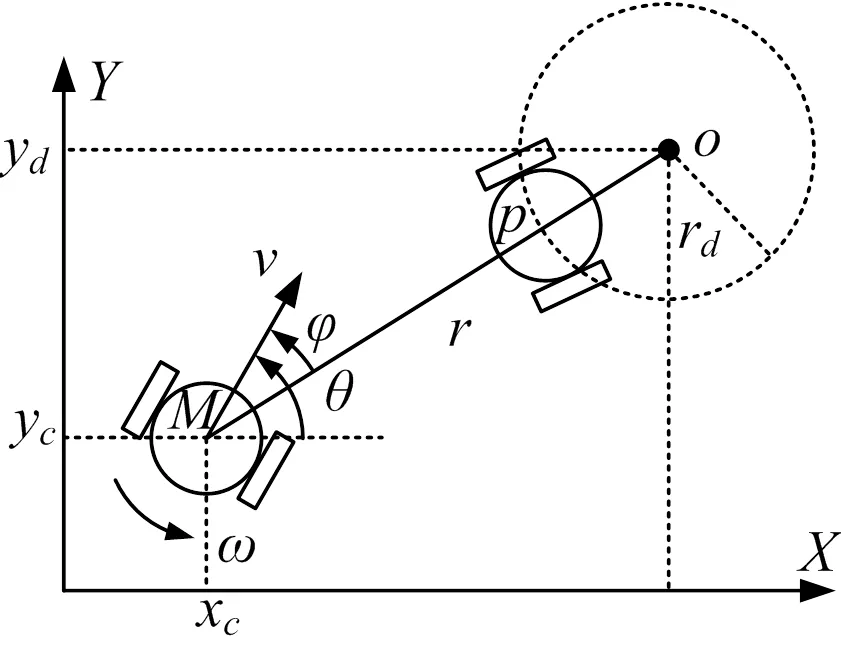
图1 双轮移动机器人

双轮移动机器人运动方程式[6]为：

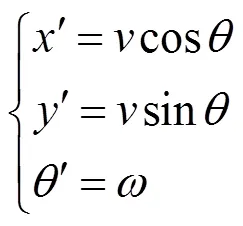
式中：(,y,)为机器人位姿。

运动误差方程式为：

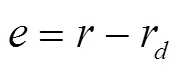
2 改进神经网络PID控制

2.1 增量式PID控制

增量式PID控制是通过控制当前时刻量和上一时刻量的差值而实现在线控制的一种算法。假设-1时刻，其控制量[7-8]为：

式中：k为比例系数；T为积分时间常数；T为微分时间常数；为采样周期。

由上式可得增量式PID控制方程式[7-8]为：

令k=kT/T，k=kT/，则PID增量方程式可以转换为：

式中： k为积分系数；k为微分系数。

2.2 BP神经网络结构

BP神经网络通过反复在线学习调整输入层与隐含层权值、隐含层与输出层权值，从而输出最小误差，其输出结构如图2所示。

图2 BP神经网络输出结构

神经网络隐含层的输出方程式[9-10]为：

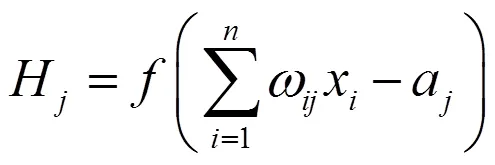
式中：为隐含层激励函数；ω为输入层和隐含层之间的权值；a为隐含层节点。

隐含层激励函数[9-10]为：

BP神经网络输出层方程式为：

式中：ω为神经网络隐含层与输出层之间的权值；b为输出层的节点。

2.3 改进BP神经网络PID控制

粒子群算法（Particle swarm optimization ）缩写为PSO，通过初始化一群随机粒子，采用迭代搜索最优值。在迭代过程中，粒子通过比较2个极值来判断是否更新粒子位置和速度，一是粒子当前最优解，称之为个体最优解；二是种群当前最优解，称之为全局最优解。粒子对比个体最优解和全局最优解来更新自身位置和速度，从而生成下一代群体。粒子速度和位置迭代方程式[11-12]为

式中：v(+1)为第个粒子迭代(+1)次的速度；v()为第个粒子迭代次的速度；x(+1)为第个粒子迭代(+1)次的位置；x()为第个粒子迭代次的位置；为惯性权重系数；1和2为学习因子，取值范围为[0,2]；1和2为随机数，取值范围为[0,1]； P为粒子的个体最优位置；为粒子种群的最优位置。

惯性权重系数会影响到局部搜索能力和全局搜索能力，为了平衡二者搜索能力，对惯性权重系数进行修正，修正后的方程式为：

式中：为粒子当前迭代次数；为粒子最大迭代次数；0为初始权重系数；1为最终权重系数。

神经网络在参数调整过程中，采用粒子群算法对神经网络权重进行优化，具体优化过程如下：

1）初始化参数，主要包括神经网络权值、网络节点个数、最大迭代次数、种群大小、粒子初始位置和速度；

2）设置输入信号，根据控制对象运动方程式，计算输出值与输入值的误差函数，得出神经网络的输入信号为：

式中：in(k)为输入值；out为输出值，()为误差值。

3）将输入信号作为神网络的输入层，调整权值ω，得到的结果传递给隐含层进行计算，最终结果通过输出层输出。

4）根据神经网络的输出值，计算PID控制器的输出()，对k、k、k参数进行调整；

5）采用改进粒子群算法更新粒子的速度和位置，并定义粒子的误差函数为；

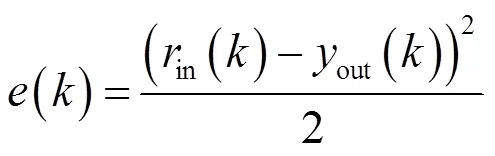
6）计算粒子的适应度函数，更新粒子搜索的个体最优和全局最优值；

7）=+1，如误差满足要求或者迭代次数达到最大值，则输出全局最优值，否则转至步骤3），直到搜索到全局最优值为止；

双轮移动机器人采用改进粒子群算法优化增量式PID控制流程如图3所示。

图3 移动机器人追踪误差控制流程

3 仿真与分析

为了验证双轮移动机器人采用PSO-BP-PID控制的效果，采用MATLAB软件对双轮移动机器人追踪轨迹进行仿真，仿真参数设置为：种群大小为100，=500，0=0.9，1=0.1，1=2=2，1=2=1，k=26.52，k=2.96，k=3.48。分别采用PID控制和PSO-BP-PID控制的阶跃响应如图4所示。假设移动机器人运动轨迹为22=4(m)。假设无外界干扰信号，分别采用PID控制和PSO-BP-PID控制的双轮移动机器人追踪结果如图4、图5所示。假设有正弦波=2sin(2π)干扰，分别采用PID控制和PSO-BP-PID控制的双轮移动机器人追踪结果如图6、图7所示。

图4 阶跃响应曲线

图5 PID追踪(无干扰)

图6 PSO-BP-PID追踪(无干扰)

图7 PID追踪（有干扰）

图8 PSO-BP-PID追踪(有干扰)

由图4可知，采用PID控制收敛速度慢，不能及时抑制外界干扰，振动幅度较大，控制系统不稳定；而采用PSO-BP-PID控制收敛速度快，能够及时抑制外界干扰，振动幅度较小，控制系统相对稳定。

由图5、图6可知，移动机器人在无干扰环境中，采用PID控制和PSO-BP-PID控制都能较好地实现双轮移动机器人运动轨迹追踪，理论与实际追踪误差较小。由图7、图8可知，移动机器人在有正弦波干扰环境中，PID控制运动轨迹追踪误差较大，而PSO-BP-PID控制运动轨迹追踪误差较小。当外界环境发生改变时，PSO-BP-PID控制产生的误差就会反馈到神经网络，通过改进粒子群算法优化PID控制参数k、k、k，从而降低追踪误差。因此，PSO-BP-PID控制方法具有调节时间短、跳动程度小、抗干扰能力强优点，能够更好地适应外界环境，不仅适合圆形运动轨迹，对于机器人其它运动轨迹同样适用，从而有效的提高移动机器人追踪精度。

4 结语

为了降低移动机器人运动轨迹追踪误差，设计了PSO-BP-PID控制方法，通过仿真对其进行验证，主要结论如下：

1）传统PID控制器缺少在线优化和参数调整，在环境受到波形干扰时，控制精度较低，不能很好地实现移动机器人轨迹追踪。

2）PSO-BP-PID控制方法，克服了存在局部最优值、收敛速度慢的缺点，可以对PID控制器参数进行在线优化和调整，抑制外界环境的干扰因素，保证移动机器人较高的追踪精度。

3）采用MATLAB软件对移动机器人追踪效果进行仿真，可以对设计效果进行检测，能够及时的发现设计不合理而进行改正，节约了成本。

[1] 李睿敏. 面向分气管焊接的桁架机器人轨迹控制研究与系统开发[D].厦门:厦门大学,2017.

[2] 徐成宇,高洪. 基于关节空间与工作空间协同的6R点焊机器人路径规划方法[J].井冈山大学学报:自然科学版, 2017,38(5):59-62.

[3] 楼巍,陈磊,严利民. 基于模糊辨识的移动机器人轨迹控制算法的研究[J].仪表技术,2013(1):18-20.

[4] 马玲,牟彬瑞. 移动机器人运动轨迹控制算法研究[J].工业仪表与自动化装置,2018(4):132-135.

[5] 李逃昌. 农业轮式移动机器人自适应滑模路径跟踪控制[J].中国机械工程,2018,29(5):579-584.

[6] 李保国,张春喜. 双轮移动机器人安全目标追踪与自动避障算法[J].控制理论与应用,2007,24(4):535-539.

[7] Zhong J, Fan J Z, Zhu Y H,et al. One Nonlinear PID Control to Improve the Control Performance of a Manipulator Actuated by a Pneumatic Muscle Actuator [J].Advances in Mechanical Engineering,2014,125(5): 369-378.

[8] 曹平军,曲林伟,王强,等. 某驱动步进电动机增量 PID 控制研究[J].舰船电子工程,2017,37(8):162-163.

[9] 杨杰群. 基于BP神经网络的情感机器人玩具的设计与实现[D].广州:华南理工大学,2014.

[10] Agand P, Shoorehdeli M A, Khaki-Sedigh A. Adaptive recurrent neural network with Lyapunov stability learning rules for robot dynamic terms identification[J]. Engineer -ing Applications of Artificial Intelligence,2017,65(10):2 -9.

[11] 刘衍民. 粒子群算法的研究及应用[D].济南:山东师范大学,2011.

[12] 张迅,王平,邢建春,等. 基于高斯函数递减惯性权重的粒子群优化算法[J].计算机应用研究,2012,29(10): 3710-3713.

Trajectory tracking control of mobile robot based on improved neural network PID control

*LI Lei1, LIU Jian-peng2

(1.School of Mechanical Engineering,Anhui Sanlian University, Hefei, Anhui 230601,China; 2. Meteorological detection system division,Anhui four creates an electronic Limited by Share Ltd, Hefei, Anhui 230000,China)

In order to improve the tracking accuracy of two-wheeled mobile robot, the improved particle swarm optimization algorithm is used to optimize the BP neural network PID controller, and the control effect is verified by simulation. The model of two wheeled mobile robot is created and the error equation of motion trajectory is given. The structure of BP neural network is added to the traditional PID control, and the particle swarm algorithm is used to improve it. The improved particle swarm algorithm is used to optimize the PID control parameters of BP neural network, and the PID control parameters optimization process of two-wheeled mobile robot is given. The trajectory tracking error of two-wheeled mobile robot is simulated and verified by MATLAB, and compared with the traditional PID control tracking error. Simulation curves show that in ideal environment, two-wheeled mobile crobots can achieve better trajectory tracking with less tracking error. In disturbance waveform environment, the tracking error of traditional PID control two-wheeled mobile robots is larger, while which of the improved PID control two-wheeled mobile robots is smaller. The improved particle swarm optimization algorithm is used to optimize BP neural network PID controller, which can improve the tracking accuracy of mobile robot.

PID control; BP neural network structure; improved particle swarm optimization; tracking error

1674-8085(2019)01-0068-05

TP243

A

10.3969/j.issn.1674-8085.2019.01.014

2018-09-29；

2018-10-19

*李蕾(1980-)，女，安徽界首人，讲师，硕士，主要从事机器人控制、微动力学系统研究(E-mail:1980leili@sina.com)；

刘建鹏(1980-)，男，安徽肥西人，高级工程师，主要从事气象雷达系统总体设计研究(E-mail:jianpeng@163.com).