一种采用改进交叉熵的多目标优化问题求解方法

2019-03-08赵舵唐启超余志斌

西安交通大学学报 2019年3期

赵舵,唐启超,余志斌

(西南交通大学电气工程学院,610031,成都)

交叉熵(Cross Entropy,CE)优化算法是一类新型的启发式随机优化算法,在优化过程中无需优化问题的梯度信息,仅根据适应度函数进行寻优,具有计算复杂度低、鲁棒性强并能以较大概率求得全局最优解的特点[1-4]。目前,有关CE优化算法的研究已经取得了一定进展,并解决了许多优化问题。在单目标优化问题的求解方面:文献[5]介绍了基本CE优化算法的原理及改进,并讨论了其在组合优化和机器学习方面的应用;文献[6]在CE优化算法的开发和迭代过程中做了改进,提高了收敛速度,并将其应用于连续变量的逆问题求解;文献[7]将CE优化算法应用于比例-积分-微分(PID)控制器的设计,并与基于遗传算法的PID控制器设计方法进行比较,结果表明CE优化算法具有较低的计算复杂度。随着研究的发展,CE优化算法逐步被拓展到多目标优化问题的求解中:文献[8]将广义分解的方法和CE优化算法结合,提出了MACE-gD算法,并与MOEA/D和RM-MEDA算法进行了性能比较;文献[9]将模糊c均值聚类算法与CE优化算法相结合,提出了改进交叉熵优化算法,并应用于解决多目标不等间距阵列综合问题;文献[10]结合了分布估计算法和CE优化算法的优点,提出了一种改进的CE优化算法,并应用于合金微钻孔加工工艺参数的多目标优化问题中,结果表明加工效率得到了有效提高。

高速和舒适是世界铁路发展的主流,因此对于高速铁道车辆横向运行平稳性的要求越来越高,被动悬挂系统逐渐难以满足使用要求,而主动悬挂和半主动悬挂控制是改善列车横向运行平稳性的有效方法[11-12]。结合我国实际,采用半主动悬挂控制系统是目前最佳的控制方法[13],半主动悬挂控制系统的参数优化对于列车横向平稳性的改善至关重要。

本文提出了采用Pareto精英个体保留排序策略以及概率分布渐进变化的多目标交叉熵优化(Multi-Objective Cross Entropy Optimization,MOCEO)算法,并将其与NSGAII[14]、SPEA2[15]、MOEAD[16]以及PAES[17]算法一同应用于经典多目标优化问题求解分析,超体积和反转世代距离指标表明了本文算法求解多目标问题的有效性。最后,将MOCEO应用于17自由度列车横向半主动控制系统的参数优化,结果表明,MOCEO具有更快的收敛速度,优化后的列车系统具有更好的横向运行平稳性。

1 交叉熵优化算法的基本思想

CE优化算法源于对小概率事件的估计,后来被拓展到求解最优化问题[18]。

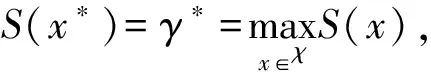
l(γ)=Pu(S(x)≥γ)=

(1)

(2)

(3)

由于g*(x)和未知的l(γ)有关,需在{f(·,u)}函数族内选择一个合适的g*(x),即选择一个参数u使得g*(x)和{f(·,u)}的距离(即CE)最小。两个概率密度函数h(x)和h′(x)之间的CE定义为

(4)

使得g*(x)和f(x,u)的CE最小的等价式为

minD(g*(x),f(x,u))=

(5)

将式(3)代入式(5),可以得到

(6)

传统CE优化算法主要包括以下步骤[19]:

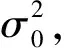
Step3 选择,计算适应度函数S(xi),i=1,2,…,N,对S(xi)进行排序得到S(1)≤S(2)≤…≤S(N),选取适应度值大的Ne个个体,作为采集的精英样本集合;

(7)

Step5 平滑处理,平滑系数α∈[0,1],更新μt和σt为

(8)

Step6 结果判断,如果max{σt}<ε(ε为方差限制边界,令ε=10-6),则程序结束返回参数μt,否则,令t←t+1,并转到Step2。

2 多目标交叉熵优化算法

MOCEO算法以CE优化算法为基础,下面详细描述MOCEO算法的组成部分。

2.1 初始化

不失一般性,考虑一个包含n个变量、m个目标的多目标最小化问题[20],具体为

(9)

式中:xi∈[xmin,i,xmax,i],i=1,2,…,n;n为决策变量的维数;m为目标函数的个数。xmin=[xmin,1,…,xmin,n],xmax=[xmax,1,…,xmax,n]分别是决策变量的上限和下限。

2.2 快速非支配排序及适应度值的分配

生成初始种群P0后,算法的主循环开始。在每次迭代过程中,首先分别计算第tc代种群Ptc中每个个体的适应度函数值,随后根据非支配排序算法确定非支配个体,并将其用于后续算法的参数更新以及个体选择。

采用外部存档机制,定义外部存档集合Atc∈RNc×n存放种群中的非支配解(或Pareto近似解),定义集合P′tc∈RM×n存放支配解,其中:种群大小Nc即为集合Atc的最大容量;M是支配解的数量,它的值在每次迭代中都不同,M≤Nc。

采用文献[14]中的快速非支配排序方法,将所有非支配解保留在集合Atc中,将所有支配解保存在集合P′tc中,由上文可知Ptc=Atc∪P′tc。当|Atc|≤Nc(本文用|·|表示集合中解的数量)时,采用非支配序作为适应度值;当|Atc|>N时,将相同非支配序的个体进行超体积贡献度计算,优先选取超体积贡献度更大的个体存入Atc,采用非支配序和超体积贡献度同时作为适应度值。超体积又称勒贝格测度,是对一系列解集的一种度量,反映了在目标空间中,这些解所共同支配的空间的大小[21]。

2.3 参数更新

2.3.2 方差向量σ2t的更新对集合Atc-1每一维的变量值分别取均值,得到

(10)

(11)

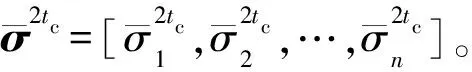
和传统的CE优化算法相同,MOCEO也使用了平滑操作来提升参数的稳定性。若平滑系数φ∈[0,1],则新的方差向量σ2tc定义为

(12)

为了保证算法更好的跳出局部收敛,取随机数r∈[0,1],如果r<0.1,则令σ2tc=βσ2tc,β为调节系数,β>1,本文取β=100。

2.4 进化方向更新

为了提高算法收敛到前沿面的速度,算法定义了方向向量,以采样个体综合算法收敛过程信息,引导算法加快寻优速度。本文通过比较进化过程中10代个体之间的差异,得到个体进化的方向信息,用以加速种群的进化过程,具体步骤如下:

(13)

Step3 使用dtc指导子代的生成,进化10代之后,返回Step1。

2.5 子代的生成

更新了均值向量μtc和方差向量σ2tc以后,按照新的正态分布模型,结合方向向量dtc,通过采样产生下一代种群Qtc。具体步骤如下。

(14)

式中:ne是适应度函数的计算次数;η为比例系数,经实验,η=0.48时效果最好;Emax为最大计算次数。

(15)

2.6 个体选择

在MOCEO迭代初期,有|Atc|≤N1,随着算法的不断收敛,落在Pareto前沿面上的个体越来越多,最终导致出现|Atc|>N1的情况,根据算法的要求需要删除集合Atc中的一些个体,使得|Atc|=N1。对于不同层间的个体,优先选择非支配序低的个体存入Atc。对于同一层间个体的优劣度的比较,采用快速排序[21]的机制来判断计算同一层每个个体对于整个种群的超体积贡献度并排序,选取贡献度较大的个体存入Atc,直到|Atc|=N1。由于快速超体积排序算法的复杂度会随着Nc的增大而呈指数级增长,为了降低算法的复杂度,减少运算时间,在算法运行前期取N1=0.3Nc,同时算法的迭代次数增加,算法的局部搜索精度提高。

2.7 结束条件

一般地,当达到算法设置的Emax时,程序停止运行,输出保存在集合Atc中的个体作为最优解集。

3 多目标交叉熵优化算法的测试与分析

为了验证算法的有效性和鲁棒性,分别针对二维ZDT[21]系列和三维DTLZ[21]系列目标测试函数,选用MOCEO、NSGA-II、SPEA2、MOEAD、PAES算法独立运算30次,计算超体积[22]和反转世代距离[16]性能指标并进行对比分析。使用Java编程语言在jMetal框架[23]中实现上述优化算法,硬件环境为Intel i7@2.6 GHz CPU,8 GB内存。

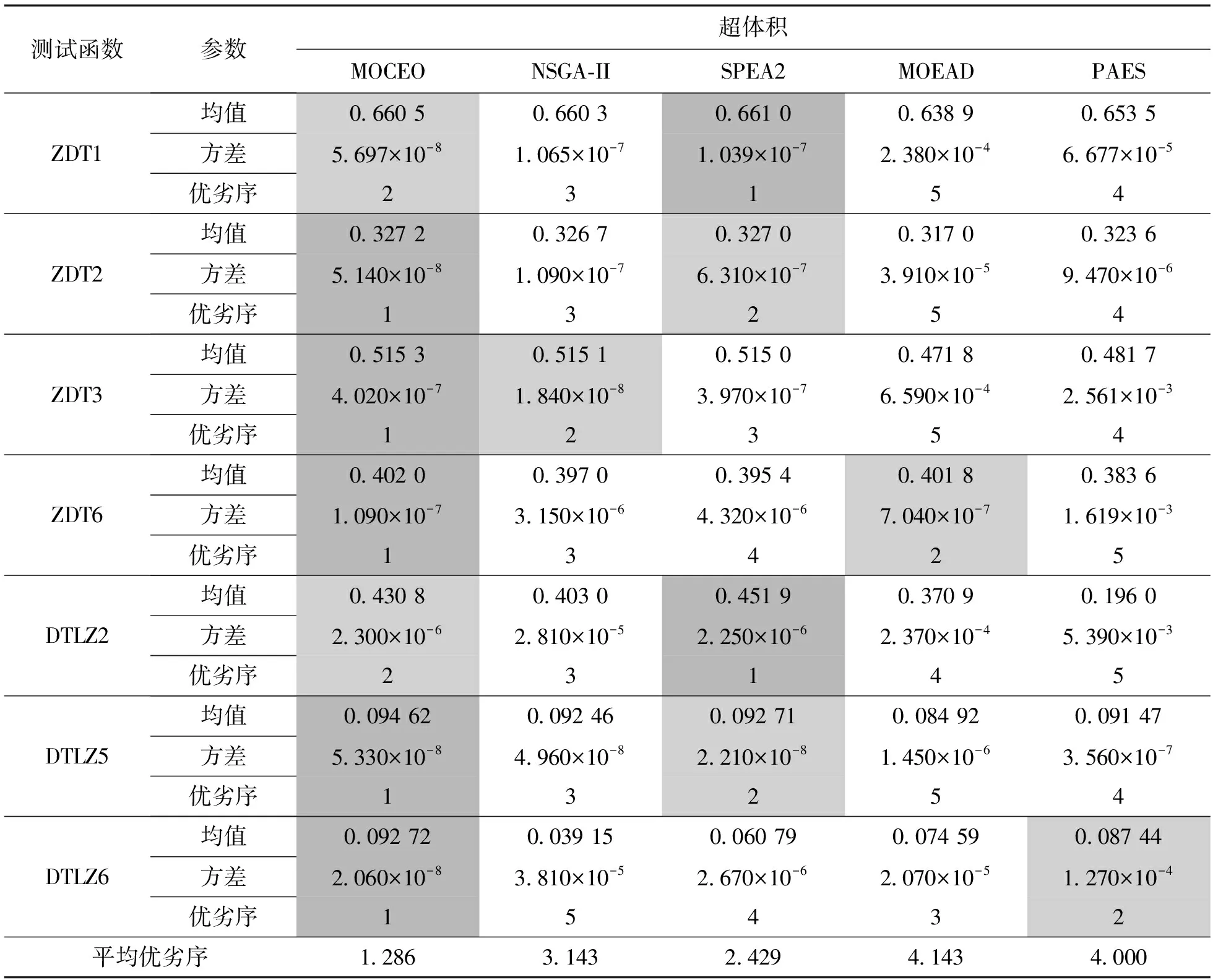
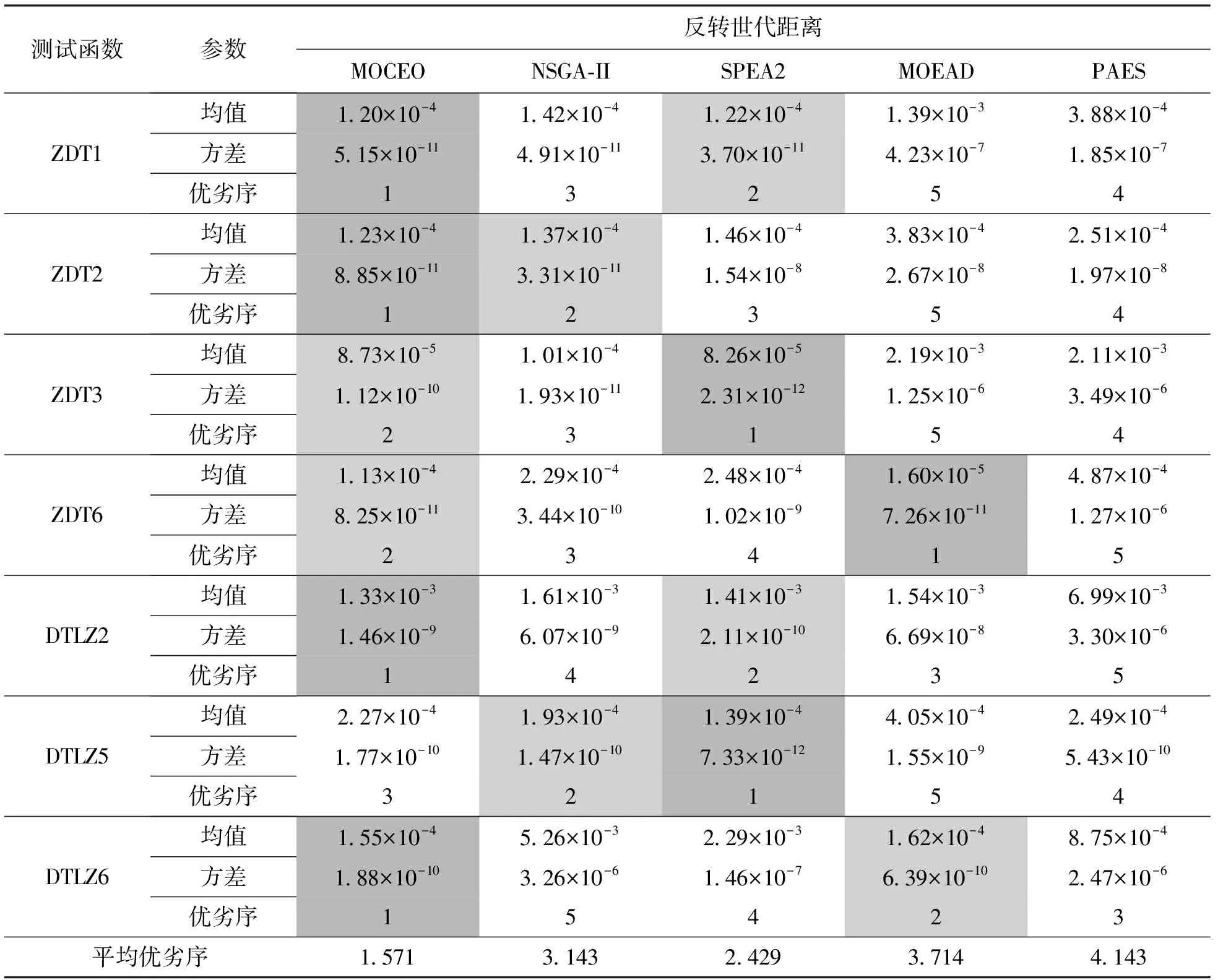
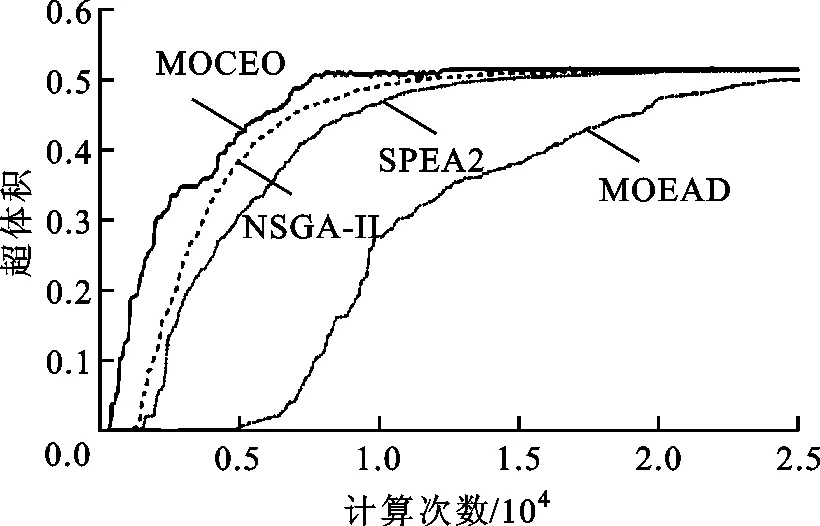
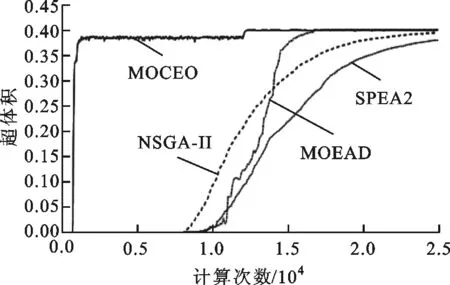
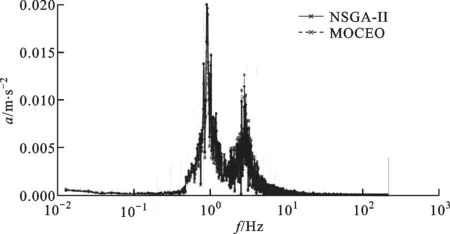
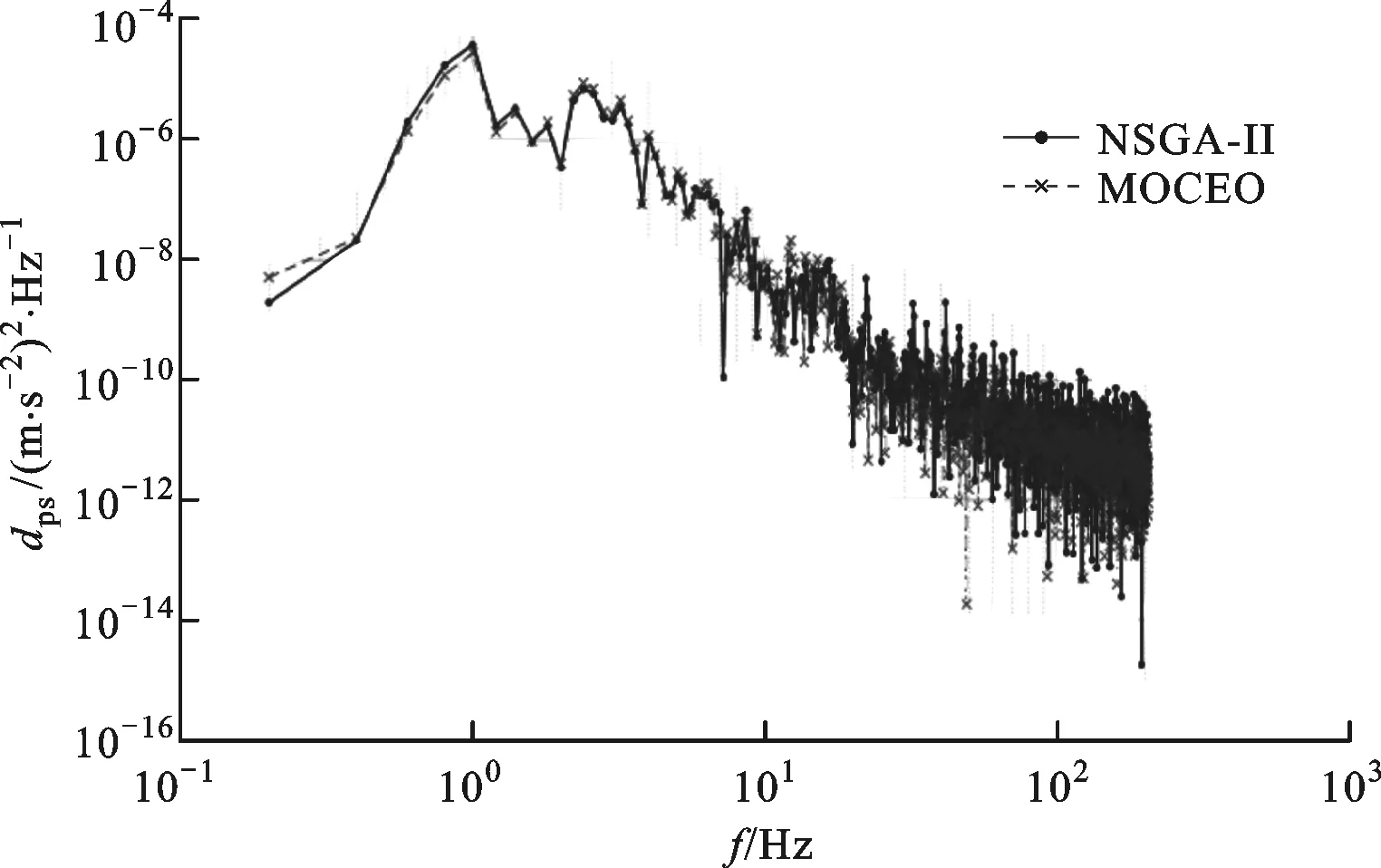
在进行仿真计算时,各算法的最大计算次数均设置为25 000。在MOCEO算法中,当适应度函数计算次数ne≤12 000时,设置种群大小Nc=100,N1=0.3Nc=30,当12 000

3.1 不同优化算法性能指标的比较

反转世代距离指标是表征进化计算获得的近似Pareto面和真实Pareto面之间的距离指标,数值越小表明近似Pareto最优解越接近真实Pareto最优解。优劣序是不同算法在同种测试函数下的性能指标的均值和方差综合排序的结果,数值越小表明算法越优秀。表1和表2分别给出了5种算法分别对ZDT系列以及DTLZ系列测试函数独立运算30次所求得的超体积和反转世代距离性能指标的比较结果(深色单元格中的数据表示最优值,浅色单元格中的数据表示次优值)。从表1可以看出,在5种算法对7种测试函数的比较中,MOCEO取得了5个最优值和2个次优值,NSGA-II、MOEAD以及PAES分别只取得了1个次优值,SPEA2取得了2个最优值和2个次优值。从表2可以看出,MOCEO取得了4个最优值和2个次优值。综上可知:MOCEO在超体积和反转世代距离指标上明显优于其他4种算法,即MOCEO得到的Pareto面具有更好的贴近度和分散性;MOCEO在30次计算得到的超体积值方差很小,即MOCEO具有更好的鲁棒性。

表1 不同算法对ZDT测试函数以及DTLZ测试函数优化结果超体积值的比较

3.2 不同优化算法收敛速度的比较

图1是MOCEO、NSGA-II、SPEA2以及MOEAD共4种算法得到的ZDT系列二维测试函数的超体积随计算次数的变化曲线,可以看出:对于ZDT1、ZDT2,MOCEO在2 500次时收敛到最优,NSGA-II和SPEA2在15 000次左右收敛到最优,MOEAD在25 000次之前没有完全收敛;对于ZDT3,MOCEO在7 500次时收敛到最优,NSGA-II和SPEA2在12 500次左右收敛到最优,MOEAD没有完全收敛;对于ZDT6,MOCEO在1 250次时收敛到最优,NSGA-II和SPEA2在22 500次左右收敛到最优,MOEAD在17 500次左右收敛到最优。由于MOCEO算法在计算次数为12 000次时种群大小由30转变为100,所以超体积在图中12 000次的位置会有一个跳变。

表2 不同算法对ZDT测试函数以及DTLZ测试函数优化结果反转世代距离的比较

(a)ZDT1测试函数

(c)ZDT3测试函数

(b)ZDT2测试函数

(d)ZDT6测试函数

图2给出了MOCEO、NSGA-II和SPEA2共3种算法在DTLZ2、DTLZ5和DTLZ6这3种三维测试函数下超体积随计算次数的变化曲线,可以看出:对于DTLZ2和DTLZ5,3种算法的收敛速度基本一致;对于DTLZ6,MOCEO在3 500次时基本收敛到最优值,NSGA-II和SPEA2基本没有收敛。MOCEO由于种群数量的变化,超体积会在12 000次时发生跳变。

(a)DTLZ2测试函数

(b)DTLZ5测试函数

(c)DTLZ6测试函数图2 3种算法在3种DTLZ测试函数下超体积变化情况

综上所述,MOCEO在ZDT1、ZDT2、ZDT3、ZDT6及DTLZ6这5种测试函数下较其他算法明显收敛速度更快,在DTLZ2和DTLZ5这2种测试函数下收敛速度与其他算法基本持平。

4 列车悬挂半主动控制系统参数优化

为了使高速列车具有更好的横向平稳性,主要采用半主动和主动悬挂的控制方法,控制器的选取及优化尤为重要。

采用文献[11]中的高速列车17自由度横向振动模型,以水平不平顺、方向不平顺及速度v为模型输入,车体横向振动合成加速度为模型输出,设置车辆运行速度v=300 km/h。采用MOCEO算法和NSGA-II算法分别对模型中的广义预测控制器[24]进行优化,选择预测时域长度P和控制时域长度P′作为决策变量,选择列车在直线轨道上轮对横移量的均方根f1、车体横向加速度的均方根f2以及列车横向平稳性指标[25]f3作为3个优化目标。设置种群大小Nd=50,迭代次数g=100,决策变量P∈(0,300],P′∈(0,300],P和P′均为正整数。

4.1 控制器参数优化结果

两种优化算法对控制器进行优化后,种群个体在空间中的分布如图3所示可以看出,MOCEO算法得到的个体解可以支配NSGA-II得到的个体解,即MOCEO算法具有更好的优化效果。对于MOCEO算法,选取图中下边界上的点对应参数作为控制器参数的优化结果,此时P=13,P′=2,平稳性指标f3为1.357 8。对于NSGA-II算法,选取图中下边界上的点对应参数作为控制器参数的优化结果,此时P=10,P′=5,平稳性指标f3为1.416 7。可见,通过MOCEO算法的优化,平稳性指标由1.416 7减小到了1.357 8,平稳性提高了4.16%。

图3 两种优化算法的解的空间分布图

4.2 两种算法优化后悬挂系统的比较

将MOCEO和NSGA-II得到的控制参数分别代入仿真模型,得到车体横向振动加速度的时域、频谱、功率谱密度,如图4所示,a表示加速度,t表示时间,f表示频率,dps表示功率密度。由图4a看出,车体横向加速度峰值由0.145 m/s2减小到0.13 m/s2,下降了10.34%。可见采用MOCEO算法优化后列车的横向平稳性得到较大改善,旅客乘坐舒适性提高。由图4b和图5c可以看出,车体横向振动加速度主要集中在0.5～5 Hz,而人体对横向振动最敏感频率范围为1～2 Hz,相比于NSGA-II算法,采用MOCEO算法优化后,在该频率范围内车体横向振动加速度明显改善。