正交异性薄板的振动能量传递特性

何理,陈天宁,陈琛

(西安交通大学机械结构强度与振动国家重点实验室,710049,西安)

正交异性薄板作为常见工程结构,其动力学特性影响着系统结构的稳定性、性能及寿命。然而,由于正交异性,薄板往往存在振动能量分布不均的问题。为了满足系统结构的设计要求,对正交异性薄板振动能量传递特性进行准确的预测分析具有十分重要的工程意义。

Nefske等在1989年预测简支梁高频振动特性时首先提出了能量有限元法(EFEM)[1],这是一种将功率流理论与传统有限元法(FEM)结合的混合建模分析方法,将结构中每一微元视作子系统,通过能量守恒定律建立结构能量密度控制方程。EFEM以能量密度为控制方程变量,避免了传统有限元法在分析高频振动时由网格密集带来的巨大计算量,因为EFEM基于波动理论,不用考虑结构模态密度,从而解决了统计能量法在中低频不适用的问题。EFEM在结构动力学高频振动分析方面独具优势。1992年,Bouthier等利用空间平均的方式将一维梁结构能量密度控制方程扩展到二维薄板结构[2-3];孙丽萍等通过能量反射与透射系数构建起结构耦合的桥梁,用于船舶高频振动分析[4]。上述研究都是针对各向同性均匀的理想薄板,而大多数实际工程的薄板结构具有正交异性:在正交垂直方向有不同的弯曲刚度,以适应在垂直方向不同的结构强度要求。直到2003年,Park等在Bouthier基础上推导出正交异性薄板的能量密度控制方程[5],并通过解析法进行了数值验证,但是却没有进一步推导能量密度控制方程的有限元形式,而且重点都是分析计算振动能量密度,对于振动能量传递特性未深入研究。解妙霞在2008年推导了圆柱壳体在轴对称弯曲振动情况下的能量密度控制方程[6];2009年,朱翔引入结构声强概念,通过有限元法对裂纹损伤结构的功率流进行研究,并实现了振动能量流动的可视化[7];张猛在2013年提出了随机参数能量有限元方法,解决了单个结构参数随机变化时梁的响应统计特性[8];2016年,Petrone等利用Nastran、Matlab软件结合求解结构声强场,分析了约束、载荷、阻尼以及正交异性对振动能量分布与传递的影响,并且进行了实验验证[9]。Wang等利用流线可视化技术,详细分析了局部阻尼作用下振动能量传递路径及对结构的影响[10]。

本文对正交异性薄板能量密度控制方程进行有限元离散处理,推导出能量有限元方程,并且通过数值算例对比经典模态法,验证了方程的正确性。求解能量有限元方程得到结构声强场,同时以流线可视化方式可直观呈现结构振动能量传递特性。应用该方法,分析了不同局部阻尼分布位置对正交异性薄板振动能量传递特性的影响。

1 正交异性薄板的能量有限元方程

1.1 二维薄板功率流理论

对于简谐激励作用下的正交异性薄板,其振动微分方程为[11]

(1)

式中:w为薄板横向位移;F为施加在板上的均布激励力;ρ为薄板密度;h为板厚;Dxc、Dyc分别为薄板沿x、y方向的复弯曲刚度;Hc为复扭转刚度。当板厚为常数时,Hc可以近似用Dxc、Dyc乘积开根号表示[11],即

(2)

式中:η为黏滞阻尼系数;Dx、Dy为薄板沿x、y方向的弯曲刚度。

基于薄板平面波远场叠加原理,能够得到式(1)关于时间平均的能量密度值。Park通过对其进行空间平均处理,推导出正交异性有限薄板的能量密度控制方程以及平均结构声强I[5]

(3)

(4)

式中:Pin为外界平均输入功率;e为平均能量密度;ω为圆频率;i、j为方向向量;Cgx、Cgy为弯曲波在板中的群速度,表达式为[5]

(5)

1.2 能量密度控制方程的有限元分析模型

通过有限元变分原理,采用Galerkin加权残值法对式(3)进行求解[12]。利用形函数N对平均能量密度e进行插值

e=N·en

(6)

式中en为单元节点处的能量密度。将能量密度控制方程转化为离散后单元的节点加权残差形式,即

∬ΩNTηωedA-∬ΩNTPindA

(7)

为了整体有限元方程求解的准确性,各节点残差值应为0。式(7)中第1项经过分部积分法和散度定理等数学转化,有如下等式

(8)

式中Γ为单元边界。为了简化方程,令应变矩阵为

BT=(

(9)

联立式(6)～(9),单元的节点残差可表示为

(10)

(11)

通过有限单元法[13]对式(10)进行组装,可得薄板能量密度整体有限元方程

(KT+KD)e=P

(12)

式中:KT为整体能量传递单元矩阵;KD为整体能量耗散矩阵;P为输入功率流向量。

由式(12)可知,能量有限元法将能量密度作为基本未知量,不再关注结构模态与弯曲波波长,网格划分不受频率影响[12],即使高频激励也不需要细密的网格。

选择平面四边形等单元,其形函数为

N=[N1N2N3N4]

(13)

式中Nm(m=1,2,3,4)为单元自然坐标系下结点形函数,结点坐标为(ξm,ζm),如图1所示。

图1 形函数自然坐标系

结点对应形函数可表示为

(14)

局部单元的自然坐标系与全局物理坐标系的转化关系式为

dA=dxdy=|J|dξdζ

(15)

(16)

式中J为坐标映射雅可比矩阵。

将式(15)(16)代入式(11),得

(17)

式中积分可由数值积分求解,从而可求得式(10),组装成式(12)即可求得正交异性薄板能量有限元方程。

2 正交异性薄板振动传递特性

2.1 正交异性薄板能量有限元方程验证

为了验证本文推导的能量有限元方程,采用与文献[5]相同的方形简支铝板为计算实例,其边长为1 m,厚度为1 mm,在普通各向同性薄板基础上沿y方向进行加强处理,其y向弯曲刚度Dy为x向弯曲刚度Dx的20倍;在薄板中心处(x0=Lx/2,y0=Ly/2)输入幅值F0=1 N、频率f=1 000 Hz的简谐激励力;结构黏滞阻尼η=0.05。采用功率级表示能量密度值

(18)

式中e0=1×10-12J/m2,为基准能量密度。

利用正交异性薄板能量有限元方程,求解得到能量密度,结果如图2所示。为了验证能量有限元法,采用文献[5]中经典模态法对相同条件铝板的能量密度进行求解,结果如图3所示。由图2、图3可知,能量有限元法与经典解析法的结果吻合较好。能量有限元法的结果相当于将经典解析法的局部细节进行了平均处理,更能体现薄板振动的整体特性,对高频振动分析更有实际意义;有限元法还适用于复杂求解域,具有工程实际意义。

由图2可知,薄板中心处为能量峰值,由于结构黏滞阻尼的存在,振动能量随距离中心能量输入点不断降低,并有明显的正交异性:由于薄板沿y方向加强,沿y方向传递时能量损失明显小于沿x方向传递时,能量流动从能量值最高处流向能量值最低处,因为沿x方向能量梯度值大,所以振动能量优先沿x方向流动。

图2 能量有限元法求得的薄板能量密度

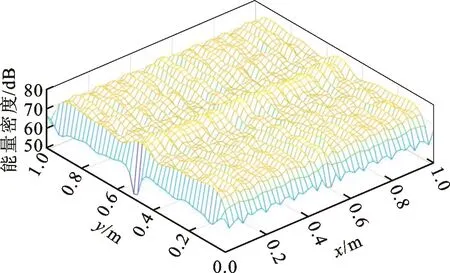
图3 经典模态法求得的薄板能量密度

2.2 局部阻尼分布对振动能量传递特性的影响

为了进一步说明振动能量的传递特性,引入流线可视化技术[10],利用平行于能量流速度方向的流线表示结构能量流动方向,表达式为

drI(r,t)=0

(19)

式中:r为能量流粒子的位置;I为结构声强,与dr平行。向量示意图如图4所示,流线与每个节点的r相互垂直,与dr相切。根据式(19),描述二维平面结构声强流线的微分方程式可写为

(20)

考虑整个薄板所有节点,多条流线组合即可绘制结构振动能量流线场图。

图4 流线上P点向量示意图

为了研究局部阻尼对正交异性薄板振动能量传递的影响,采用算例铝板,修正其结构阻尼系数使得η=0.001,在局部阻尼单元处,增加其阻尼系数使得η=0.5。考虑3种典型局部阻尼分布位置,研究其对振动能量传递的影响[14],局部阻尼分布如图5所示。图中网格为求解薄板能量有限元方程时所划分,大圆表示能量输入单元,小圆表示局部阻尼单元,数字1、2、3表示3种不同阻尼分布情况:第1种局部阻尼单元与能量输入单元呈对角线分布;第2种局部阻尼沿x方向分布;第3种局部阻尼沿y方向分布,其中能量输入单元的位置保持不变。

图5 局部阻尼分布示意图

当局部阻尼与能量输入单元为第1种分布时,正交异性薄板振动能量传递特性如图6所示,图中黑色流线表示振动能量流线场,描述薄板振动能量从能量输入点到能量耗散点的流向轨迹,流线由振动能量输入点处向周围扩散,由于阻尼耗能,流线在阻尼点汇聚。云图为薄板结构声强向量的幅值,颜色变化对应幅值大小变化,颜色越浅能量密度越高,颜色越深能量密度越低,描述了振动能量在薄板的大小以及分布。由于整体结构阻尼系数较小,振动能量峰值与最低值变化不大。

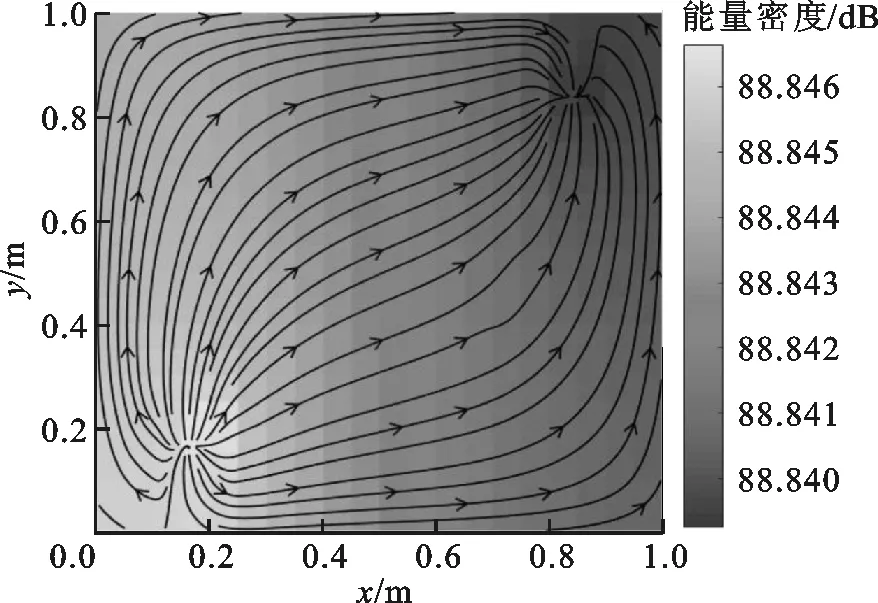
图6 阻尼分布于1处的结构声强流线场图

由图6可知:振动能量在输入单元处能量密度达到峰值,形成能量源,不断向外扩散振动能量;在局部阻尼单元处能量密度值为局部低谷,由于阻尼作用不断耗散振动能量,形成能量槽[10],将结构周围振动能量吸收;由于薄板沿y向做了加强处理,流线场流向优先沿x向传递,表现出明显的正交异性。

当局部阻尼单元与能量输入单元为第2种分布时,正交异性薄板振动能量传递特性如图7所示。类似第1种分布方式,云图中激励输入单元颜色最浅,能量密度为峰值;阻尼单元颜色最深,能量密度为局部低谷;流线图则清晰表示出振动能量如何从激励输入单元流向局部阻尼单元,不同的是能量流向出现明显差异:在靠近能量源与能量槽一侧,能量呈现快速下降,振动能量流线为直线;在远离能量源与能量槽一侧,能量传递受到材料正交异性的影响,振动能量流线为弧线,整体类似于磁场。

图7 阻尼分布于2处的结构声强流线场图

当局部阻尼单元与能量输入单元为第3种分布时,正交异性薄板振动能量传递特性如图8所示。类似前2种分布方式,振动能量从激励输入单元流向局部阻尼单元,局部阻尼单元对结构振动能量的耗散范围从整块板缩小到板的1/3。正交异性将阻尼对薄板结构振动能量吸收阻隔,从而在远离能量源与能量槽一侧,振动能量随薄板扩散而不是流向局部阻尼单元。薄板结构声强幅值出现小幅改变,振动能量峰值有所降低而振动能量最低值有所增加。局部阻尼位置对正交异性薄板振动能量分布以及传递路径有重要影响,通过上述方法可以绘制出任意能量输入与局部阻尼位置下正交异性薄板的能量分布以及能流传递路径。

图8 阻尼分布于3处的结构声强流线场图

3 结 论

本文针对正交异性薄板中的高频振动问题,引入结构声强概念,对正交异性薄板能量密度控制方程进行有限元离散处理,推导出正交异性薄板能量有限元方程,并且通过数值算例对比经典模态法,验证了方程的正确性;然后,求解能量有限元方程得到结构声强场,同时以流线可视化方式更直观地呈现结构振动能量传递特性;最后,应用该方法分析了不同局部阻尼分布位置对正交异性薄板的振动能量传递特性的影响。通过算例分析得出如下结论:正交异性材料属性改变了振动能量传递路径,振动能量优先沿弯曲刚度较小方向流动;局部阻尼分布位置对振动能量分布以及传递路径有重要影响,决定了振动能量流向以及整体能量分布。