九轴联动叶片双刀铣削刀路平滑算法

宋冬冬,薛飞,赵万华,卢秉恒

(西安交通大学机械制造系统工程国家重点实验室,710054,西安)

叶片是汽轮机的关键部件,其型面多由扭曲的自由曲面构成,细长、薄壁特性使其在加工过程中易产生弯曲和扭转变形,严重影响叶片的加工质量和加工精度[1-2]。目前,已有诸多学者针对工件加工变形的控制方法开展了大量研究,包括改善夹具结构以提高工件加工过程中的刚度[3-4],改变切削参数[5-6]、刀轴矢量[7]来优化切削力大小和方向,以及通过加工过程中的误差补偿[8-9]优化切触点的位置等,在一定程度上控制了加工变形,从而提高了加工精度。

五轴加工具有灵活自由度、良好材料去除率,适用于叶片类曲面的加工,但五轴加工的轨迹对加工表面质量有较大影响。传统的五轴轨迹规划方法有等参数法[10]、等平面法[11]和等残留高度法[12]。文献[13]提出了一种等高线的路径生成方法,通过曲面上的标量函数生成一系列等高曲线,探讨多目标约束下的函数求解问题,实现全局最优的刀具路径规划。文献[14]以切削区域切削力的阈值为约束条件,建立自由曲面全局最优的五轴加工路径优化算法以提高加工效率,然而在路径规划中易于出现冗余的刀具运动轨迹。文献[15]定义切削宽度和进给速度为两个独立的函数,使路径规划问题转化为全局最优函数的求解问题,但复杂曲面的轨迹规划有一定的局限性。加工轨迹的优化能够在一定程度上改善工件的加工质量,但加工精度和效率的相互影响限制了加工质量的持续提高。

双刀加工为解决加工精度和效率的矛盾提供一种新的思路。森精机公司在双刀头卧式加工中心NT4300DCG[16]上,采用与DP Technology公司在CAM软件ESPRIT上合作开发的后置处理程序[17],实现了叶片型面7轴联动的双刀螺旋高效加工。西安交通大学研究了一种兼顾加工质量和加工效率的双刀对顶铣削方法,并提出了基于切削力抵消的轨迹优化算法[18],为叶片型面的高效加工提出了一种全新的解决方法。文献[19]提出双刀纵切加工系统的实现方案及轨迹规划方法,规划了叶片型面的双刀加工轨迹。但上述方法都以切削力抵消作为轨迹规划的基础,存在轨迹规划算法计算量大、刀轨和刀轴不平滑的问题,影响了叶片的加工质量。

因此,本文提出了基于几何约束的叶片型面双刀对铣轨迹平滑算法,由双刀具的结构约束,建立了双刀轴矢量的统一表征模型,结合等残留高度和等弦高误差规划的参数增量,提出相邻切触点间参数增量的等参化求解算法,并以叶片两侧曲面对应加工区域同时完成铣削为约束条件阐述了双刀加工轨迹的参数匹配优化算法。以某汽轮机叶片为例,规划了双刀对铣粗加工轨迹,通过仿真和实验分别验证了双刀加工轨迹的可行性,且叶片型面的轮廓误差均无超差现象。

1 叶片双刀对铣原理和实现方法

叶片双刀对铣是在叶盆和叶背曲面的加工区域内,采用刀具1、刀具2对顶同步铣削实现叶片型面的高效加工,原理如图1所示。叶片型面粗加工工艺分为双刀对顶纵向铣削叶盆、叶背曲面和单刀纵向铣削叶片进、出汽边。

图1 双刀对铣原理示意图

结合双刀对铣刀具的位置关系,考虑叶盆和叶背曲面的不对称性,双刀加工系统各轴的运动关系模型如图2所示,OwXwYwZw为工件坐标系。刀具B具有沿X、Y、Z方向运动的直线轴和绕Y轴旋转的B轴,刀具C具有沿U、V、W方向运动的直线轴和绕V轴旋转的C轴,两把刀具共用绕X轴旋转的工件回转A轴,通过9轴联动确定双刀具的姿态以实现双刀具对顶同步铣削。

图2 双刀加工系统运动轴位置图

2 双刀刀具姿态的统一表征和求解

双刀共用A轴,如图2所示,以OwXwYwZw为基准,刀具B、C分别在叶片两侧不同高度且平行于XwOwZw的平面内摆动,即两把刀具在YwOwZw平面内的投影相互平行。刀具B、C的姿态在双刀加工系统中相互约束,需实现统一表征。

2.1 双刀刀轴矢量的统一表征

在OwXwYwZw中,叶盆曲面和叶背曲面上相对的两切触点法向矢量分别为n1=[x1,y1,z1]、n2=[x2,y2,z2],如图3所示,且n1、n2在YwOwZw平面内的投影分别为m1=[0,y1,z1]、m2=[0,y2,z2],则m1、m2的夹角为

图3 刀轴矢量的结构约束关系

(1)

刀具B、C的刀轴矢量分别为a1、a2,在YwOwZw平面内的投影分别为b1、b2,由双刀具的结构约束可得b1、b2的夹角为π。设m1、b1的夹角为φ1,m2、b2的夹角为φ2,则有

φ1+φ+φ2=π

(2)

沿着φ增大的方向分别绕Xw轴旋转角度φ1、φ2,使得m1、b1重合,m2、b2重合,即

(3)

(4)

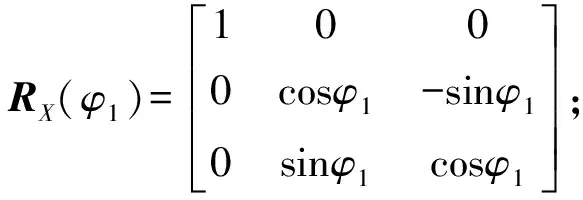
根据向量与坐标轴的几何关系,设切触点处法向矢量和刀轴矢量具有相同的X轴分量,则a1、a2的解析表达式为

(5)

(6)

由式(5)(6)可知,参数φ1影响a1、a2的姿态,在参数x1、x2已知的情况下,计算了所有满足机床结构约束的刀轴矢量。

2.2 刀具姿态定义

在切触点C处建立局部坐标系OLXLYLZL,如图4所示,XL轴为瞬时切削方向,YL轴为曲面C点处的法线方向,由XL、YL轴按右手法则确定ZL轴,前倾角αL为刀具轴线绕ZL轴的旋转角度,侧偏角λL为刀具轴线绕YL轴的旋转角度。

图4 刀轴矢量的定义方法

在OLXLYLZL中,假设f为XL的单位矢量,n为YL的单位矢量,a为刀轴矢量的单位矢量,则αL、λL可分别表示为

(7)

式中:f=[xf,yf,zf];n=[xn,yn,zn];a=[x,y,z]。

2.3 有效切削半径的表征

多轴联动加工引起刀轴矢量变化而改变了牛鼻铣刀的实际切削形状,如图5所示。在局部坐标系OLXLYLZL中,牛鼻铣刀的有效切削半径[20]为实际切削形状在切触点处与瞬时切削平面Pf、Pk相交轮廓线的曲率半径。平面Pf为XL、YL确定的平面,平面Pk为YL、ZL确定的平面。步距方向和行距方向的有效切削半径Re1、Re2为

(8)

式中:R为牛鼻铣刀半径;r为圆角半径。

以局部曲面的结构特征为约束,为避免铣削过程中邻近曲面间产生过切现象,则Re1、Re2满足

(9)

式中:ρXL=0、ρZL=0分别为局部曲面在平面Pk、Pf内的曲率半径。

图5 牛鼻铣刀的有效切削半径

结合叶片型面的几何参数,考虑双刀轴矢量的约束关系,由式(8)(9)可计算满足双刀铣削要求的前倾角和侧偏角取值范围。

3 双刀加工轨迹平滑算法

3.1 参数增量的定义

在多轴铣削过程中,行距方向的切削宽度取决于允许的残留高度、有效切削半径和曲面局部曲率半径,如图6所示。假设cd(i-1,j)为叶背曲面第i-1条轨迹上第j个切触点,ρud(i-1,j)为该点u向曲率半径,Red(i-1,j)为有效切削半径;cb(i-1,j)为叶盆曲面第i-1条轨迹上第j个切触点,ρub(i-1,j)为该点u向曲率半径,Reb(i-1,j)为有效切削半径。叶背和叶盆曲面上第i-1与第i条轨迹线间的切削宽度分别为

(10)

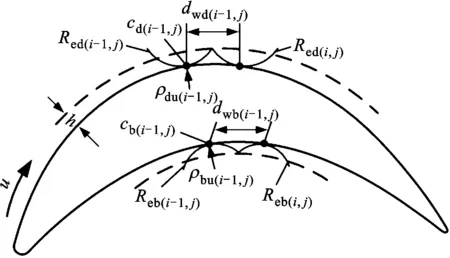
图6 残留高度和切削行距示意图

在切削步长方向上,以离散点间直线逼近曲线的弦高误差控制刀具切削的步长,如图7所示,轨迹线上的切削步长l(i,j-1)满足

(11)

式中:ε为弦高误差;ρv(i,j-1)为第i行轨迹线上第j个切触点c(i,j-1)在v向的曲率半径。

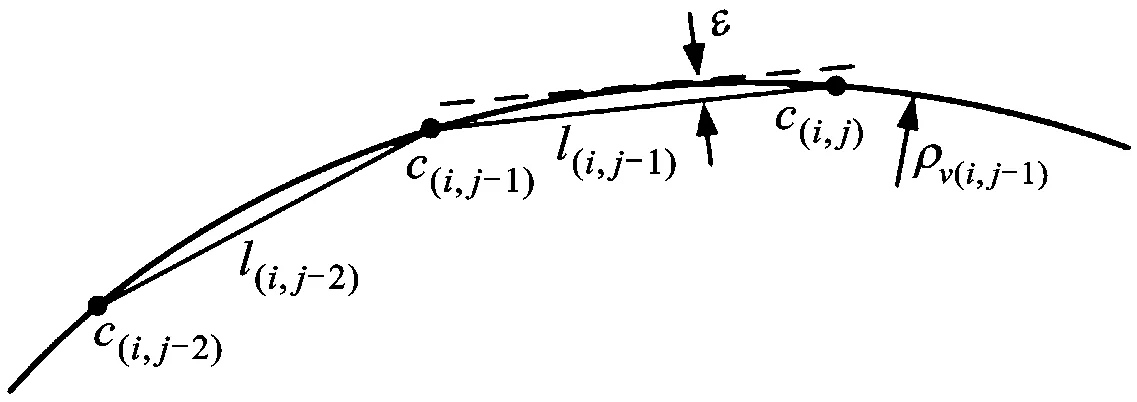
图7 弦高误差和切削步长示意图

叶片型面双刀铣削轨迹线如图8所示,选择型面的u向为行距方向,v向为步长方向,Ld、Lb分别为叶背、叶盆曲面的铣削宽度,td(i)、td(i-1)为叶背曲面上第i、i-1条轨迹线,tb(i)、tb(i-1)为叶盆曲面上第i、i-1条轨迹线。cd(i-1,j-1)的参数坐标为[ud(i-1,j-1),vd(i-1,j-1)],cb(i-1,j-1)的参数坐标为[ub(i-1,j-1),vb(i-1,j-1)]。在u向上,叶背和叶盆轨迹线间的参数增量为

(12)

式中:Sd、Sb分别为叶背、叶盆曲面的参数方程;dwd(i-1,j-1)、dwb(i-1,j-1)分别为叶背和叶盆曲面上第i-1、i条轨迹线间的切削宽度。

v向叶背、叶盆轨迹上的参数增量为

(13)

式中:ld(i-1,j-1)、lb(i-1,j-1)为叶背和叶盆曲面第i-1条轨迹线上第j-1、j个切触点间的切削步长。

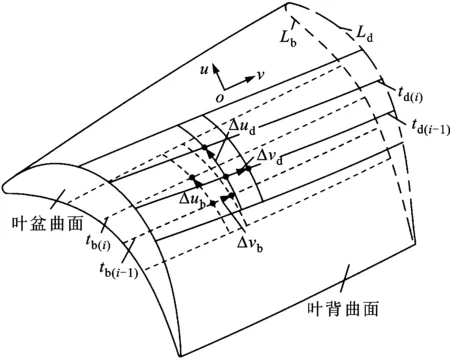
图8 叶片型面双刀铣削轨迹线示意图

3.2 单行切触点轨迹平滑算法

由于叶背和叶盆曲面上各切触点处曲率、有效切削半径的不同,即使残留高度和弦高误差相同,Δu、Δv也不相同,单行切触点呈现出沿行距方向参数不等的现象,引起切触点轨迹线的不平滑,参数增量如图9所示。在u向上,仅以残留高度为约束计算Δudi、Δubi,这不能保证双刀加工过程中叶片型面上切触点轨迹的平滑,进而影响型面的加工质量。

(a)叶背曲面

(b)叶盆曲面图9 轨迹线间切触点的参数增量

为了满足单行切触点轨迹线平滑的要求,并兼顾加工质量和加工效率,对Δudi、Δubi进行等参数化求解,叶背和叶盆曲面任意相邻轨迹线间在行距方向的参数增量分别为

(14)

式中N为相邻轨迹线间的切触点数。

以叶片曲面首条轨迹线为基准,通过式(14)所得参数增量值来规划单行切触点的轨迹线,进而规划整个曲面的光滑轨迹线。同时,通过式(11)(13)规划轨迹线上的初始切触点,对Δvdi、Δvbi进行等参数化求解,则叶背和叶盆曲面沿步距方向上任意相邻切触点间的参数增量分别为

(15)

3.3 双侧参数匹配的轨迹优化算法

叶片曲面上各切触点沿u、v向等参数化的参数增量实现了加工曲面切触点轨迹线的平滑,但叶背和叶盆曲面加工区域的面积不同,在参数域内沿u向的参数取值范围存在差异,且任意相邻两条轨迹线间的等参数值不同,仅保证单行轨迹线的平滑,难以实现叶背和叶盆曲面上的轨迹线条数和切触点数量一致。为了满足叶盆和叶背曲面加工区域同时完成铣削的要求,需研究双刀对顶铣削参数匹配的轨迹线平滑算法。

为了保证叶片两侧曲面具有相同的轨迹线条数,在u向上取Δud、Δub的较小值作为基准参数,满足

Δumin=min(Δud,Δub)

(16)

同时,设置自定义的比例系数

(17)

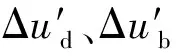
(18)

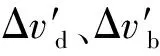
(19)

通过式(18)(19)分别计算任意相邻轨迹线间和对应轨迹上相邻切触点间的参数增量值,进而实现了叶背和叶盆曲面对应加工区域内轨迹线条数和切触点个数相同的目标。

4 典型零件的验证

4.1 叶片型面双刀加工轨迹规划及仿真

以不锈钢材质的汽轮机叶片作为研究对象,叶片型面的长度为633 mm,回转直径为165 mm,型面的粗加工轮廓度公差为[-0.3 mm,0.3 mm]。牛鼻铣刀的半径R为16 mm,圆角半径r为6 mm。残留高度h的允差为0.05 mm,弦高误差ε的允差为0.02 mm。采用双刀加工轨迹平滑算法规划叶片型面的双刀对铣粗加工轨迹,任意相邻轨迹线间的参数增量值不相等,但任意两条轨迹线具有相同的参数增量值,且轨迹线满足刀路平滑的要求,如图10所示。通过多次测试该算法规划双刀加工轨迹的时间,对比文献[19],计算效率提高了56%。

(a)叶背曲面轨迹线 (b)叶盆曲面轨迹线图10 叶片型面双刀加工轨迹线

基于VERICUT软件建立了双刀加工机床的仿真模型,采用叶片型面的双刀对铣粗加工轨迹进行加工过程仿真,结果表明:两把刀具在叶背和叶盆曲面实现了同步铣削,且同时完成两个曲面上加工区域的铣削;双刀铣削过程中无干涉,且加工表面刀痕纹路整齐,无过切现象。

针对双刀仿真铣削的已加工叶片型面,随机选取均匀分布在叶盆和叶背曲面上理论测量点坐标,计算理论点与仿真加工曲面上实际测量点在法向方向上的距离偏差值,并表征测量点处的轮廓误差,结果如图11所示。叶盆和叶背曲面的轮廓误差为[-0.008 mm,0.038 mm]、[-0.008 mm,0.042 mm],均满足公差要求。由于叶盆曲面为凹曲面,叶背曲面为凸曲面,参数增量值相同,叶背的切削宽度大于叶盆的,且型面加工区域u向参数范围不同,所以叶背曲面的残留高度大于叶盆曲面,加工型面与理论型面之间的距离偏大,型面的轮廓误差较大。

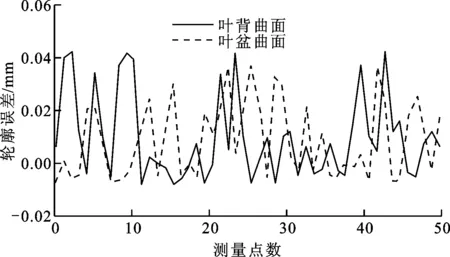
图11 叶片型面仿真轮廓误差

4.2 双刀铣削实验验证

九轴联动叶片双刀加工机床如图12所示,刀具B有独立的3个直线,刀具C有1个旋转运动。用4.1节的参数来规划整个叶片的双刀加工轨迹,采用牛鼻铣刀开展实验,验证双刀加工轨迹在实际铣削过程中的可行性。该算法规划的双刀加工轨迹实现了叶片两侧曲面双刀对顶铣削过程,满足叶片型面加工区域完全铣削的要求,且已加工的区域与理论规划的区域一致,整个铣削过程中无干涉,但铣削后的叶片型面呈现不平整的现象,存在可见的振纹,如图13所示。

图12 九轴联动叶片双刀加工机床

(a)叶背曲面

(b)叶盆曲面图13 双刀加工后的叶片型面

针对实际加工后的叶片型面,随机选取均匀分布在叶盆和叶背曲面上理论测量点的坐标,采用HEXAGON公司的Global Performance 7107三坐标测量机测量理论点所对应已加工叶片型面上的实际坐标值,计算实测、理论坐标值的距离偏离量,并表征已加工型面的轮廓误差,结果如图14所示。叶背、叶盆曲面的轮廓误差为[-0.029 mm,0.07 mm]和[-0.029 mm,0.063 mm],均满足公差要求。实际加工的轮廓误差略大于4.1节中仿真所得的轮廓误差,这可能是由拍振、刀具磨损及应力释放等原因造成的。

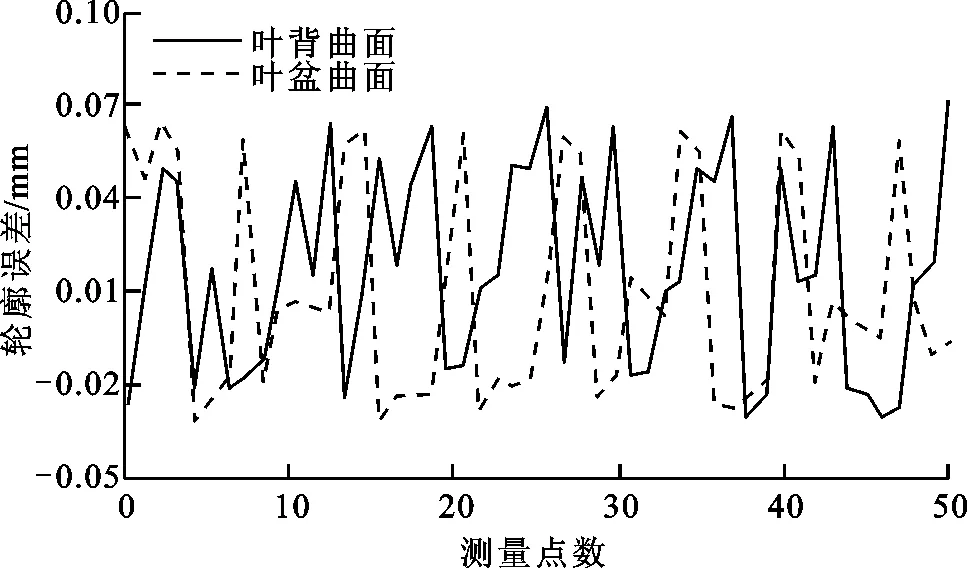
图14 已加工叶片型面的实测轮廓误差

为了测试双刀铣削的加工效率问题,采用等效的切削参数分别在双刀加工机床上实测双刀铣削和单刀铣削的加工时间,约为4.8、8.2 h,该工序双刀对铣相对单刀的加工效率提高了约41.5%,且满足轮廓误差的公差要求。

5 结 论

本文提出了基于几何约束的叶片型面双刀对顶铣削轨迹平滑算法。利用九轴联动双刀加工机床中两把刀具的结构约束关系,由切触点处的法向矢量表征了双刀具姿态的刀轴矢量。结合等残留高度和等弦高误差定义的参数增量,确定了切触点间等参数化的参数增量,实现了单行切触点轨迹的平滑。由叶背和叶盆曲面切削区域的范围确定参数匹配关系,形成了双侧参数匹配的轨迹优化算法,满足叶片两侧加工区域同时完成铣削的要求。针对典型汽轮机叶片,规划了双刀粗加工轨迹,该算法的计算效率提高了56%。仿真和实验结果表明,粗加工轨迹可实现叶片型面的双刀加工,且已加工表面的轮廓误差均在公差要求的范围内,双刀加工相对单刀加工的效率可提高约41.5%。