混合智能算法的多目标无功优化方法

曹裕捷 张彬桥

(1.三峡大学 电气与新能源学院，湖北 宜昌 443002；2.梯级水电站运行与控制湖北省重点实验室，湖北 宜昌 443002)

电力系统无功优化(ORPF)是典型的多变量多约束的非线性高维规划问题[1]，常规优化方法如内点法[2]、非线性规划法[3]等处理ORPF 并不理想，收敛性较差、计算量大、耗时多且易陷入局部最优.源于仿生思想的智能算法如遗传算法[4]、粒子群算法[5]、差分进化算法[6]等被引入ORPF求解并取得了较好效果.

相比根据偏好信息加权将多目标无功优化转化为单目标问题再求解的传统方法，基于帕累托(Pareto)最优[7]的多目标智能算法不需事先权衡各目标函数的偏好参数即可搜索得到一系列帕累托最优解，避免了严重依赖经验的参数试探工作，在无功优化领域得到了广泛应用.目前，相关研究主要集中在引入并改进单一智能算法的多目标无功优化.文献[8-9]采用快速非支配解排序遗传算法及其改进算法(NSGA、NSGAII)求解以最小化有功网损和电压偏移为目标的多目标无功优化模型，在局部最优解与全局最优解间达到动态平衡；文献[10-11]将无功电压控制问题视为混合整数非线性优化问题加以处理，通过扩展PSO 算法使其能解决连续和离散变量混合控制问题，基于全面学习思想改进步长更新策略以避免算法早熟并提高收敛能力；文献[12-13]采用改进强度帕累托进化算法(SPEA、SPEAII)进行多目标无功优化，并在目标函数中考虑了碳排放和调度经济性指标；文献[14]引入多目标差分进化算法求解以系统网损最小、电压偏移最低、电压稳定裕度最高为目标的多目标无功优化模型，取得了比传统加权法更为理想的优化结果.但实际应用表明，随着无功优化目标函数在迭代过程中的性质变化，单一智能优化算法无法保证各个寻优阶段的全局适应性和鲁棒性及性能优势.若能使多种智能优化算法在不同进化阶段优势互补，有望得到更好的多目标无功优化结果[15].

本文综合分析多种智能算法在整体搜索能力、收敛速度、适应性和鲁棒性等方面的特征，提出一种基于多种智能算法动态混合策略的多目标无功优化方法(HIA)，以适应不同寻优阶段各算法优势特征，提高整体寻优效率.将新方法应用于IEEE30节点系统进行各项优化指标的算法对比测试，证明新方法在多目标无功优化过程的全局表现更优.

1 多目标无功优化的数学模型

电力系统无功优化的目标函数有多种不同形式.为对比方便，本文选取常见的系统网损最小和电压偏移最优目标，分别建立如式(1)、(2)所示的多目标无功优化模型.

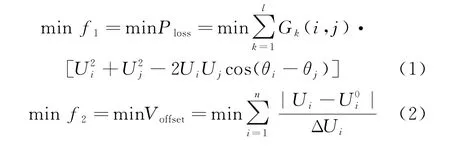
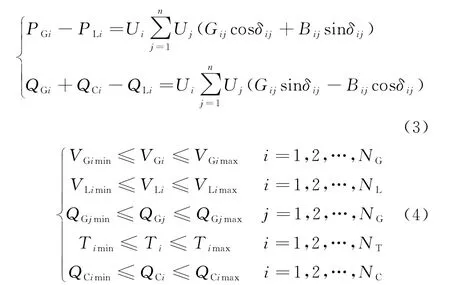
式 中 ，Ploss为 系 统 有 功 网 损 ，Voffset为 节 点 电 压 偏 移 ，l为系统总支路数，n为除平衡节点外网络节点总数，Gk(i，j)为节点i和j之间的电导，Ui、Uj分别为节点i和j的电压，U0i为i节点的给定电压值，ΔUi为i节点电压给点最大偏移值，θi和θj分别为节点i和j相角.

电力系统无功优化的状态变量包含发电机无功出力和各节点电压，控制变量包括发电机发出无功功率大小和发电机节点电压水平、电容器组投切以及可调变压器变比.这些状态变量和控制变量受公式(3)所示的潮流方程等式约束和公式(4)所示的可调范围不等式约束.

式中，PGi是发电机注入有功，PL是负荷消耗有功，Gij和Bij分别是节点i、j间支路电导和电纳，NG、NL、NT、NC分别为发电机节点、负荷节点、可调变压器节点、补偿电容器节点数量，VGimax和VGimin是发电机电压的上下限，VLimax和VLimin是负荷电压的上下限，QGjmax和QGjmin是发电机无功出力的上下限，Timax 和Timin是可调变压器变比的上下限，QCjmax和QCjmin是无功补偿容量的上下限.

2 智能优化算法的动态混合策略

2.1 备选多目标智能算法集

多目标智能优化算法是一类庞大的算法家族，用其进行无功优化的基本思想和计算流程也类似，但在全局和局部搜索能力、跳出局部最优解能力和收敛速度等方面却各有优势.根据文献[15]的实验结果，本文选取代表性的粒子群算法(PSO)、遗传算法(GA)、差分进化(DE)和导向搜索算法(OSA)构成备选算法集进行对比研究，综合分析并绘制4种算法计算特性的优劣势五边形图，如图1所示.五边形的5个顶点(A、B、C、D、E)分别表示算法的5个评判标准及其优劣程度.图1清晰反映出4种算法的局限性及其可能的互补性.通过对基本思想和计算流程都具备共性的智能优化算法进行恰当混合，在不同优化阶段采用不同优化算法产生子代个体，可望实现多种算法优势互补以提高整体寻优效率.

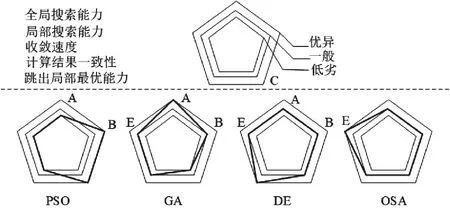
图1 智能算法计算特征示意图

2.2 Pareto最优与个体适应度

多目标无功优化的目标函数兼顾经济和电压稳定，且难以确定各目标函数权重，其解不唯一，即不存在经济性和电压稳定同时最优的解，而是一组非劣解的集合，称为Pareto最优解集.具体定义如下：

多目标最优问题的目标函数为F=minfi(x)，i=1，2，…，n.其中，fi(x)为第i个目标函数，n为目标函数的数量.当且仅当满足公式(5)时，认为x1支配x2，记作x1≺x2.

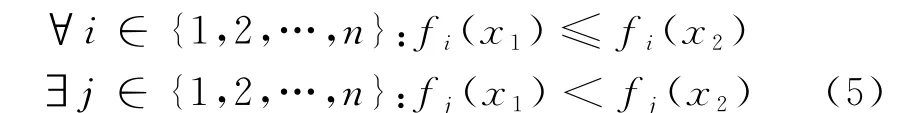
在多目标优化问题中，通常是在一个特定的集合中讨论解的Pareto最优.例如集合S={xi，i=1，2，…，n}，若x∈S，且不存在x'∈S使x'≺x，则把x称为集合S的非支配解.包含所有非支配解x的集合P称为S的Pareto最优解集.所有非支配解对应的目标函数值称为Pareto前沿，如式(6)所示.

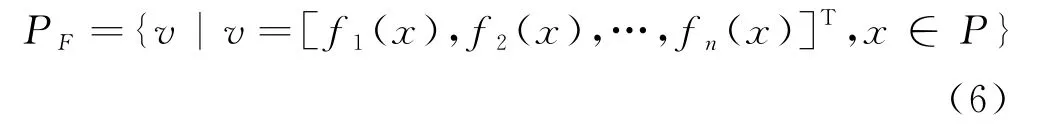
可见，多目标无功优化即寻找一组控制变量的Pareto最优解集.在智能优化算法种群迭代过程中，可基于Pareto最优概念来判断个体的优劣程度，为支配更多个体的个体分配更优的适应度.

2.3 智能算法动态混合策略

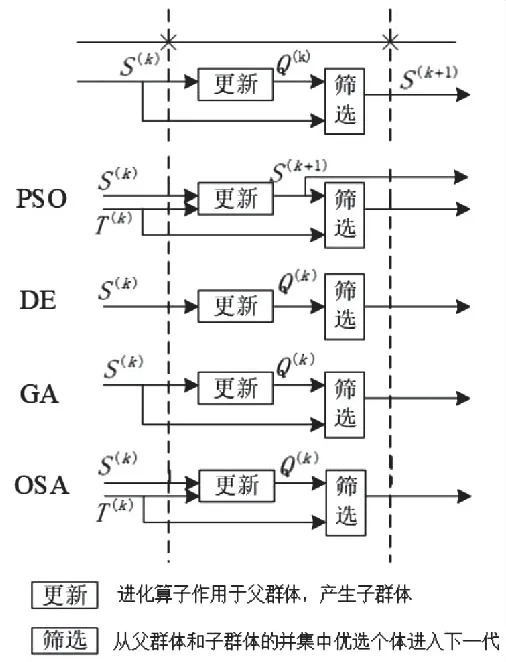
图2 智能算法动态混合过程

3 多目标无功优化的混合智能算法实现

3.1 编码和越限处理

所有备选无功优化智能算法统一采用混合实数编码，连续控制变量可在其上下限范围据实取值，离散控制变量就近取整.发电机节点电压幅值UG(连续变量)、并联电容器补偿容量QC(离散变量)和可调变压器变比tT(离散变量)的初始种群混合实数编码见式(8).

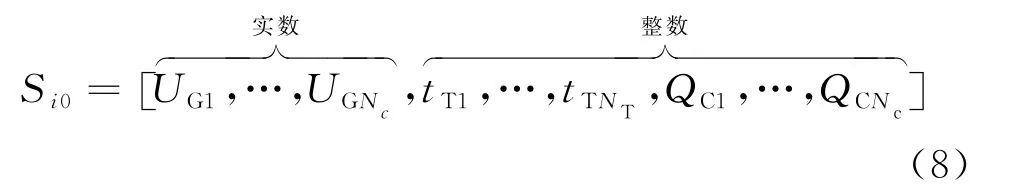
通过Pareto支配关系进行个体适应度分配并确定备选算法使用比例.迭代过程中，当控制变量和状态变量如无功功率QG和节点电压Ui越限，即违背等式和不等式约束公式(3)和(4)时，采用式(9)所示的罚函数进行校正，令F较小的个体支配F较大的个体.

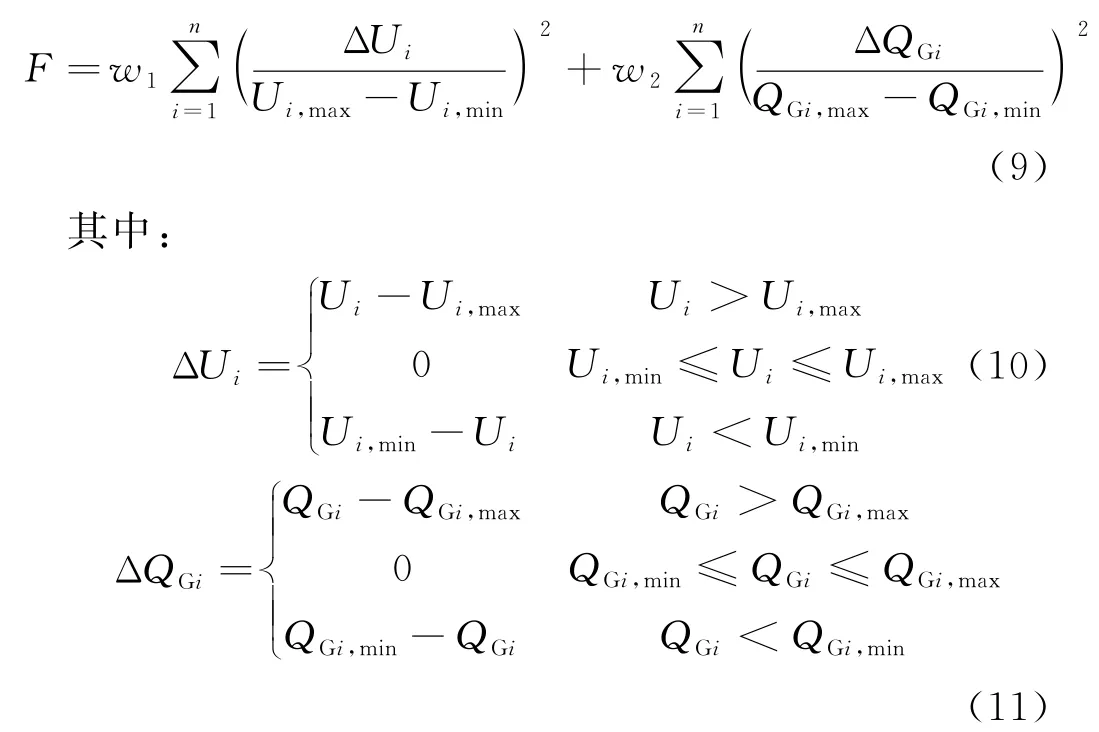
Ui，max、Ui，min、QGi，max、QGi，min为相应越限量的上下限；w1、w2为除PV 节点外的节点电压和发电机无功越限罚因子，通常可设为0.5.

3.2 具体算法流程

基于混合智能算法的多目标无功优化过程如下：

(1)系统和种群初始化：输入目标电力系统及控制变量参数，形成用于潮流计算的节点导纳矩阵；生成规模为n的初始种群S(k)，k=0，最大迭代次数T.

(2)目标函数计算：对S(k)的个体用牛拉法计算系统潮流，根据式(1)、(2)计算系统有功网损和电压偏移，若违反式(3)、(4)，则根据式(9)计算越限罚函数值.

(3)进化计算：根据S(k)中个体之间的Pareto支配关系进行适应度分配；按照式(7)和图2步骤，将备选算法j(j=1，2，…，J)作用于父群体并从结果中随机选取数量为的个体构成，合并所有得到新种群Q(k).

(4)对Q(k)的个体进行潮流计算，求得目标函数值和罚函数值.合并S(k)和Q(k)，得到R(k).

(5)计算规模为2n的种群R(k)中个体之间的Pareto支配关系并据此分配个体适应度，并根据适应度值筛选n个优势个体进入下一代群体S(k+1).

(6)迭代，k=k+1，若k＞T，则优化过程结束；否则转到步骤(3).

基于混合智能算法的多目标无功优化计算流程图如图3所示.

4 算例分析

4.1 算例及参数

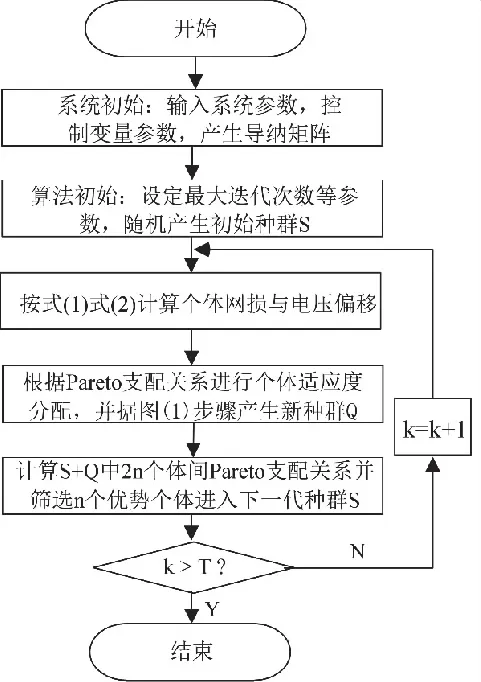
图3 混合智能算法的多目标无功优化计算流程图

为验证混合智能算法(HIA)求解多目标无功优化问题的有效性，本文采用IEEE 30节点系统进行混合算法和单一PSO、GA、DE、OSA 算法的多目标无功优化仿真计算并对结果进行分析比较.IEEE 30节点系统如图4所示，系统控制变量参数见表1.

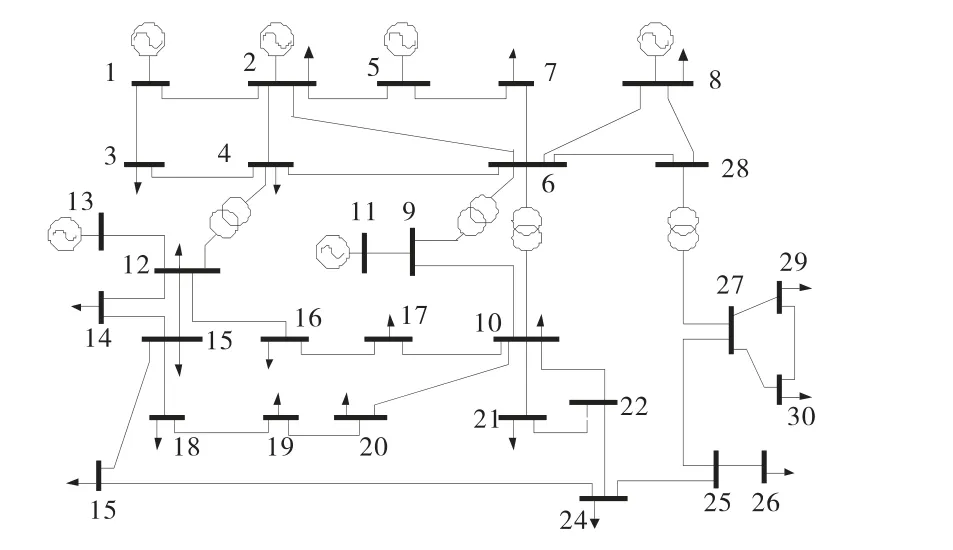
图4 IEEE 30节点系统

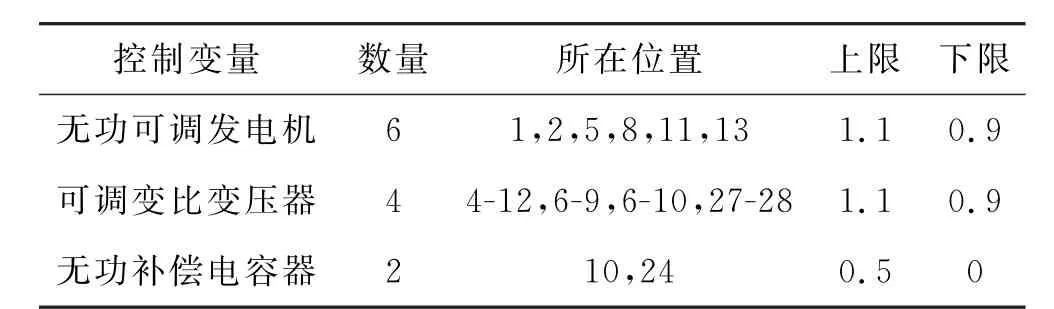
表1 IEEE 30节点系统控制变量

控制变量采用实数编码，初始种群规模和迭代次数设置为100，GA 算法的交叉和变异概率分别设定为0.8与0.02，交叉和变异参数取20，PSO 算法的惯性权重0.5+rand/2，加速系数均设置为1.5，DE 算法的交叉概率和变异系数取0.5和0.3，OSA 算法的导向邻域控制参数线性变化.

4.2 Pareto前沿对比

图5是HIA 和PSO、GA、DE、OSA 5种算法用于IEEE 30 节点系统多目标无功优化获得最终代Pareto前沿.由图5容易发现HIA 相比其它4种算法获得了更优的Pareto前沿：Pareto最优解集在目标空间大致沿一定曲线趋势展开，所含候选解不仅数量众多且分布范围广阔均匀，网损和电压偏移目标函数值也最靠近坐标轴.

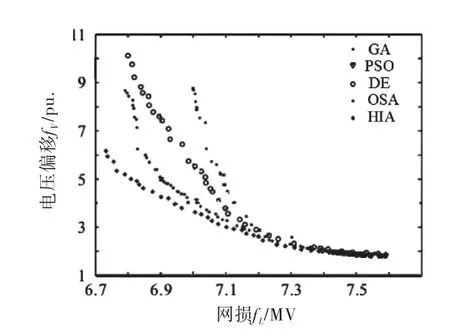
图5 5种算法的Pareto前沿

Pareto前沿提供了不同目标维度下的多个候选解，供决策者在不同运行背景下灵活选取.由于目标函数的优化包括网损和电压偏移，可根据实际需要在满足网损及电压偏移某个目标前提下取另一目标的最优值.针对本算例，可在满足网损小于6.8 MW 前提下比较电压偏移；或满足电压偏移小于3.6 pu.时比较最小网损.按上述两种比较方式选出图5中各算法满足条件的最优解及其网损和电压偏移目标函数值见表2.

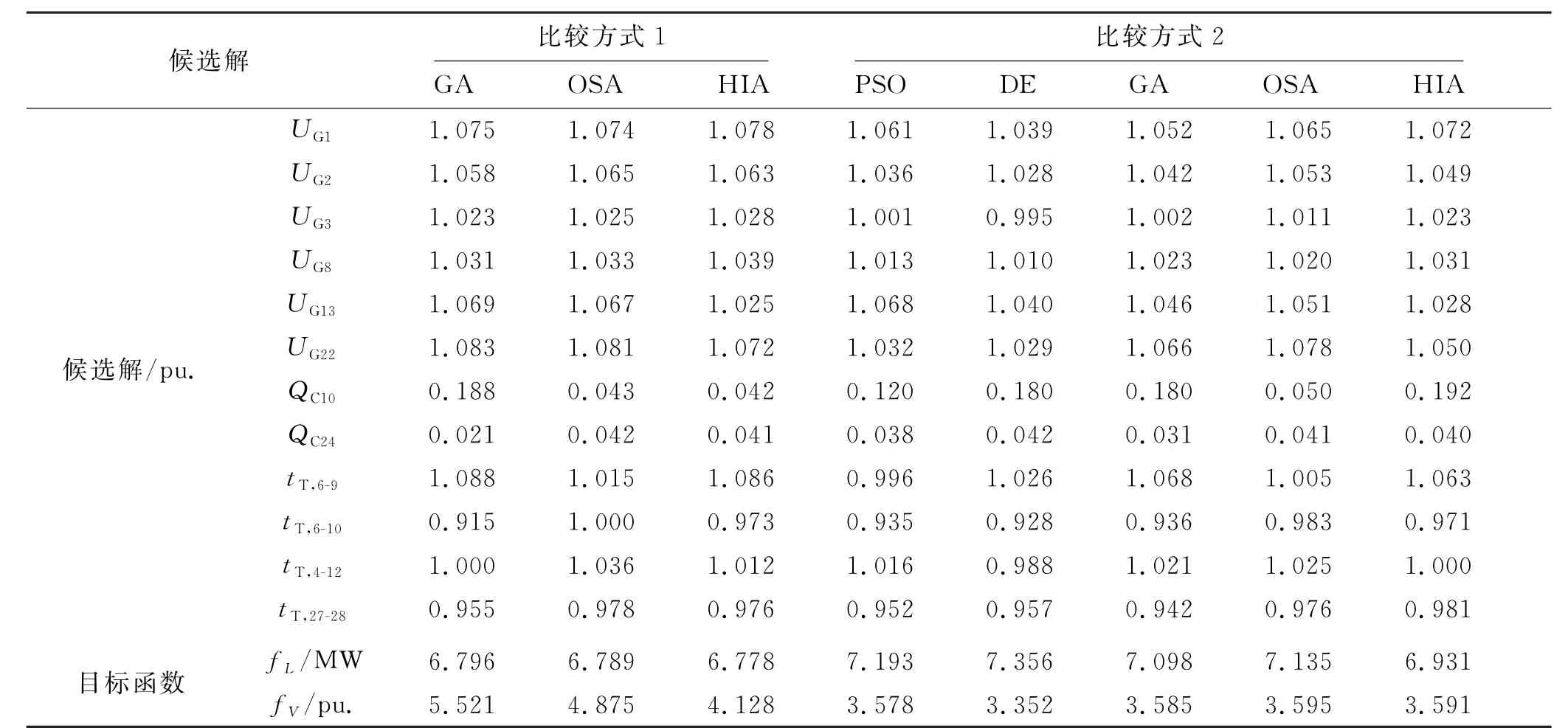
表2 两种比较方式下的最优解

方式1当满足网损小于6.8MW 时，HIA 获得了各对比算法中最小电压偏移4.128pu.，PSO 和DE则没有获得网损小于6.8MW 的解.方式2当满足电压偏移小于3.6pu.时，系统最小网损仍然是HIA 获取的6.931MW 最优解.两种比较方式都表明基于混合智能算法的多目标无功优化方法的寻优结果最好.

4.3 外部解比较

Pareto前沿无法反映算法的收敛速度，需进一步比较各算法多次计算的外部解.本例中的外部解定义如式(12)、式(13)所示.

考虑到智能算法的随机性，将各算法独立运算60次，每次迭代次数100，按式(12)、式(13)可分别在每代得到fL与fV的60个外部解取其均值，绘制有功网损fL与电压偏移fV外部解的代际收敛曲线与盒须分布，如图6～7所示.

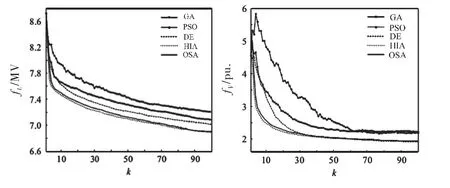
图6 网损和电压偏移的外部解收敛曲线

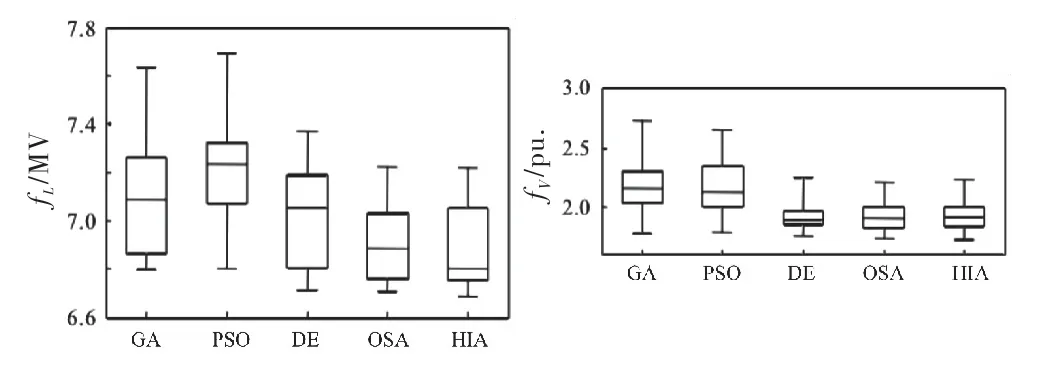
图7 网损和电压偏移的外部解盒须图

由图6可知，无论系统网损还是电压偏移，HIA相比其它算法都具有更快的收敛速度，曲线更靠近坐标轴且最终获得的外部解均值最小，最终Pareto前沿分布范围更广.盒须图常用来表达解集个体的分布情况，其矩形区域覆盖50%的样本，矩形中线表示解集的中位数，上下边缘分别表示解集的上下四分位数.通过观察图7所示盒须图可知，HIA 外部解集不仅具有更小中位数，且解的分布显示出更好的集中性，说明算法的稳定性和一致性较好.

5 结 论

基于混合智能算法的多目标无功优化新方法，通过多种智能优化算法动态混合策略增大迭代过程中优势算法的使用比例以产生更多的优势个体，提高整体寻优效率.将新方法用于标准IEEE30节点系统多目标无功优化，并从Pareto前沿、外部解收敛速度及分布情况等方面与单一算法的优化结果进行比较，新方法获得了最优的Pareto前沿并具备更好收敛性.新方法未考虑特定算法的不同组合效果，后续可进一步研究多种算法协同互补的内部机理和适配特性以建立更优的算法组合备选池和组合策略.