典型燃料点火延迟时间的一阶和二阶局部和全局敏感度分析

席双惠，王 繁,＊，李象远

1四川大学原子与分子物理研究所，成都 610065

2四川大学化学工程学院，成都 610065

1 Introduction

Sensitivity analysis (SA)1–9is an important tool in model validation and evaluation and it provides quantitative information on importance of input parameters in a model on its outputs.The first-order sensitivity coefficient describes effect of one input parameter on model output,while the second-order sensitivity coefficient represents interactive effect between two parameters on the output1.SA has been employed extensively in analysis of chemical kinetic models for combustion processes.In those analysis,input parameters in the model are reaction rate parameters,thermodynamic data or transportation parameters and outputs of the model are combustion characters predicted by the model such as ignition delay time,laminar flame speeds,and concentration of critical species under various combustion conditions.Sensitivity analysis is also closely related to uncertainty analysis1,2,5,6.There is always some uncertainties in the input parameters of a chemical kinetic model.Effects of these uncertainties on the predicted combustion properties can be revealed with the help of sensitivity analysis.On the other hand,uncertainties of the input parameters should be considered when carrying out sensitivity analysis.Such uncertainty analysis has become rather popular recently10–16.In addition,SA has also been employed to develop reduced mechanisms by removing redundant species and reactions through local rate sensitivity analysis or directed relation graph aided sensitivity analysis17–23.

Sensitivity analysis is divided into local sensitivity analysis and global sensitivity analysis.In local sensitivity analysis1–5,response of the model output due to a small change of the input parameters from their nominal values is evaluated.Local sensitivity coefficients for concentration of species,temperature or pressure in a chemical kinetic model satisfy certain differential equations in a spatially homogeneous,dynamic system and they can be determined by solving the corresponding equations numerically.This approach has been implemented in software packages such as Senkin24.On the other hand,when sensitivity of some global combustion characters such as ignition delay time is required,brute-force method is generally employed25.Sensitivity coefficient of an input parameter is determined from difference between the original model output and the output with the input parameter varied by a fixed percentage in this method.A total number of (m + 1) model runs need to be carried out to determine the first-order local sensitivity coefficients of m input parameters.In principle,both first- and second-order local sensitivity coefficients can be obtained.However,only first-order local sensitivity analysis has been reported previously for chemical kinetic model of combustion.In those first-order local sensitivity analyses,the input parameters are allowed to vary only in a small range so that linear sensitivity coefficients can be calculated.However,nonlinear effect could be important particularly when the input parameter can change in a relatively large range,or when uncertainty of an input parameter is large.In addition,coupled effects of two input parameters are not considered.

To circumvent these problems,global sensitivity analysis can be carried out1–3,5,10,16,26–30.In global sensitivity analysis,the input parameters are allowed to change in a much larger space,or the whole uncertainty range and coupling between two input parameters is also evaluated.A large number of model runs are usually required in global sensitivity analysis where all the investigated input parameters vary simultaneously within the whole range of their possible values.Several methods have been developed to perform global sensitivity analysis8,10,11,16,26–28,31,32Global sensitivity analysis through an optimized high-dimensional model representation method using a random sampling of inputs(RS-HDMR) has been implemented in the GUI_HDMR program by Ziehn and Tomlin10,26,29–35.A relatively small number of samples is needed to carry out global sensitivity analysis using the GUI_HDMR program and it is presently one of the most popular global sensitivity analysis method in analysis of combustion models26,29,30,33,34,36–46.Recently,the artificial neural network method28has been adopted to further reduce computational effort in HDMR method.However,a relatively large number of samples are still required compared with local sensitivity analysis and global sensitivity analysis is rather expensive particularly when the number of input parameters is large.In practical calculations,global sensitivity coefficients with respect to the most important 20–30 input parameters in the chemical models for combustion processes are calculated with GUI_HDMR26.In a chemical kinetic model for combustion process,there usually exist several hundreds or even thousands of input parameters and the most important 20–30 input parameters are chosen based on physical consideration or firstorder local sensitivity coefficients.Third-order or even higherorder sensitivity coefficients can be determined in principle with HDMR,however,only first and second-order global sensitivity coefficients are calculated in practice26,29,30,33,34,36–46.

The output of the model is written as a polynomial function of the input parameters in RS-HDMR and global sensitivity coefficients are calculated from this polynomial function26.A large number of samples is employed to obtain the parameters in this polynomial function through Monte-Carlo integration in RSHDMR.In fact it is possible to determine this polynomial function by only varying two input parameters simultaneously if the first- and second-order sensitivity coefficients are to be determined.When this polynomial function is available,firstand second-order sensitivity coefficients in both local and global sensitivity analysis can readily be achieved.The number of samples can be reduced dramatically with this approach and it is also possible to obtain sensitivity coefficients for a larger number of input parameters.Global sensitivity coefficients determined in this way are different from those using RS-HDMR,where some averaged effects are included.In this work,we propose to calculate first and second order sensitivity coefficients of ignition delay time of some hydrogen carbon fuels with respect to reaction rate constants in corresponding combustion kinetic mechanisms using this approach.These sensitivity coefficients can provide valuable information on effects of a single reaction as well as interactive effects of two reactions on ignition delay time.

This paper is organized in the following manner:the method employed in this work as well as computational procedures to obtain sensitivity coefficients are provided in Method Section.The first and second-order sensitivity coefficients for ignition delay time of some important fuels:H2,methane,n-butane and n-heptane under different combustion conditions are provided in Results and Discussion Section.Sensitivity coefficients in local sensitivity analysis are compared with those in global sensitivity analysis in this section.Conclusion will be drawn in Conclusion Section.

2 Method

In the HDMR method for global sensitivity analysis,the output of the model f(x) is represented as a function of the input parameters based on the idea of analysis of variance(ANOVA)40decomposition using the following form:

In Eq.(1),n is the number of input parameters,f0is the zeroth order component function which represents the mean effect of the input parameters on the output of the model,fi(xi) is the first order component function and represents independent effects of each input parameter xion the output f(x),fij(xi,xj) is the second order component function which describes correlated effects of both xiand xjon f(x).f1,2,...,n(x1,x2,...,xn) in Eq.(1) accounts for the n’th order correlated effects on f(x).For most systems,the HDMR expression up to the second-order can provide a satisfactory approximation for f(x)47:

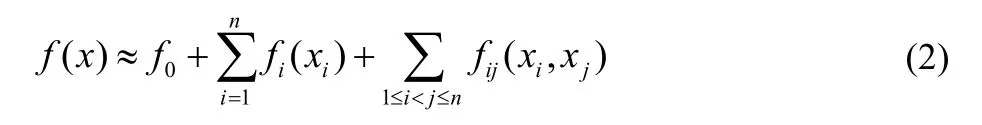
In previous works,each input parameter is always rescaled to be in the range of [0,1].We prefer to rescale the input parameters so that all xisatisfy -1 ≤ xi≤ 1 and the input parameter is zero when it takes its nominal value in this work.Advantage of rescaling the input parameters in this way will be manifested in the following.

In the GUI-HDMR software,the first- and second-order component functions are further approximated from linear combinations of a set of orthonormal polynomials {φp(x)} over the range of the scaled input parameters:

where u,v and w are the orders in the polynomial expansions,are the expansion coefficients.In the present work,we employ exactly the same relations,i.e.,Eqs.(2)–(4) to approximate relationship between the output of the model and the input parameters.Legendre polynomials which are orthogonal over the range of [-1,1] are chosen for the set of orthonormal polynomials {φp(x)} and they satisfy the following equations:

The first and second-order global sensitivity coefficients are defined from the ratio between the partial variances and the total variance using the following equations:

Siis the first order global sensitivity coefficient,or the main effect of the input variable xion the output;and Sijis the secondorder global sensitivity coefficient,or the interaction effect of xiand xjon the output.We only consider the first- and the secondorder sensitivity coefficients in calculations and all these global sensitivity coefficients add up to 1:

One can see from the above equations that the global sensitivity coefficients are determined from the expansion coefficientsin Eqs.(3) and (4).According to their definition in Eqs.(7)–(10),global sensitivity coefficients are always positive.In the RS-HDMR approach,these coefficients40,41as well as the zeroth order term f0are determined from Monte Carlo integration over the input sample.

In fact,f(x) expressed in Eqs.(2)–(4) is fully equivalent to an expression expanded with a set of ordinary polynomials:

Considering that xiis zero when the corresponding input parameter takes its nominal value,it can readily be seen from Eq.(12) that B0is the value of the output when all the input parameters take their nominal values.In addition,can be determined from samples where only the i’th input parameter is different from its nominal value,whilecan be obtained from samples by only varying the i’th and j’th input parameters.When the expansion coefficientsandare determined,the expansion coefficientscan be calculated using the following equations:

The first- and second-order global sensitivity coefficients can thus be achieved fromusing Eqs.(8)–(10) and Eqs.(12)–(14).To determine,we only need to vary one- or two-input parameters in the model runs.This means firstand second-order global sensitivity analysis can possibly be carried out from samples where only one or two input parameters change their values at the same time.The number of samples can be reduced significantly using this procedure.

In local sensitivity analysis,the output of the model with respect to the input parameters is expressed using the following Taylor expansion3:

We focus on first- and second-order sensitivity coefficients of ignition delay time with respect to reaction rate constants in this work.The brute-force approach is usually employed to obtain first-order local sensitivity coefficients in previous works using the following equation:

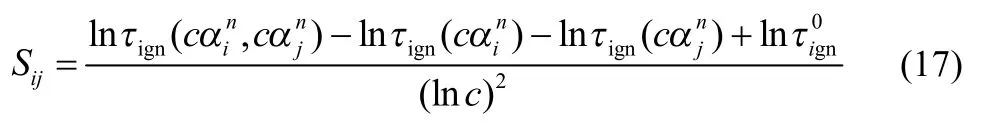
In the present sensitivity analysis,the output of the model f(x)is chosen to be lnτignand the input parameters are the natural logarithm of the factor that scales the reaction rate constant.The input parameters are restricted in the range of [-1,1] and the factor that scales the reaction rate constant is thus in the range of[1/e,e] where e is the base of the natural logarithm.It is straightforward to scale the reaction rate constants in a larger range,or in its uncertainty range and still map the input parameters in the range of [-1,1].

According to Eq.(12),B0is simplyin this work.To determine,we only need to run simulations on ignition delay times with scaled reaction rate constant for the i-th reaction.can be obtained from ignition delay times with scaled reaction rate constants for both the i-th and the j-th reaction.In the present work,the orders u,v and w in the polynomial expansions are set to be 4.The input parameters only vary in a small range and setting the orders to be 4 should provide reliable sensitivity coefficients.Higher order may be required if the input parameters are allowed to change in a much larger range.are obtained from ignition delay times with the i-th reaction rate con stant scaled by 1/2,1/2,2and 2.On the other hand,are determined from ignition delay times with both the ith and the j-th reaction scaled by these four factors.The expansion coefficientsare calculated using Eqs.(13) and(14) and the first- and second-order local and global sensitivity coefficients are achieved from these expansion coefficients.To account for the first- and second-order sensitivity coefficients of m input parameters,a total number of (8m(m - 1) + 4m + 1)model runs are required.One can also choose smaller numbers for u,v and w in Eq.(12) initially and increase them only when necessary.Number of model runs can possibly be reduced in this way.

3 Results and discussion

First and second-order global and local sensitivity coefficients for ignition delay time of H2,methane,n-butane and n-heptane with respect to reaction rate constants at various initial conditions are studied using the approaches described in Method Section.Global sensitivity coefficients calculated from Eqs.(8)–(14) will be termed as GSA,while the first-order global sensitivity coefficients with only theterm in Eq.(13) are represented with GSA-1.Global sensitivity coefficients with GSA-1 are those only considering the first order terms in global sensitivity analysis.LSA denotes traditional local sensitivity coefficients based on Eqs.(16) and (17) with the constant c taken to be e,while the local sensitivity coefficients determined fromare represented by LSA-1.Lists of the ten important reactions or reaction pairs on ignition delay times of these fuels under various conditions are given in tables in supporting information and they are discussed in detail in the following.

3.1 Sensitivity analysis on ignition delay time of H2

A small-size mechanism for combustion ofincluding 10 species and 33 reactions is employed for sensitivity analysis.Ignition delay times in a zero-dimensional closed homogeneous reactor27with constant pressure are simulated under the initial conditions of T = 1000 K,p = 1 Pa,φ = 1.0;T = 1000 K,p = 40 Pa,φ = 1.0;T = 1400 K,p = 1 Pa,φ = 1.0;and T = 1400 K,p = 40 Pa,φ = 1.0,respectively.First- and second order sensitivity analysis with respect to reaction rate constants of the 33 reactions were carried out for ignition delay times under these four conditions.

3.1.1 First-order sensitivity coefficients

Reactions with the largest absolute GSA and LSA for ignition delay time of H2under these four conditions are illustrated in Fig.1.It can be seen from this figure that the most important reactions on ignition delay times obtained from GSA are almost the same as those with LSA,except for reaction No.11 (H +O2(+ O2) = HO2(+ O2)).This reaction is rather important using LSA on ignition delay time at T = 1400 K and p = 40 Pa,while it is of minor importance with GSA.In fact,this reaction is shown to be the third most important reaction on ignition delay time at this condition using GSA-1,where the correlated effects of two input parameters are not considered.According to our results,difference between important reactions using GSA-1,LSA and LSA-1 are negligible for H2.This shows results of firstorder global sensitivity analysis using the present approach are affected to some extent by presence of higher order terms in expansion for f(x) in some cases.

One can see from Fig.1 that the chain branching reaction:H +O2= OH + O is always one of the most important reaction on ignition delay time.On the other hand,HO2and H2O2play a more important role in combustion of H2at higher pressures.These results are consistent with previous findings on combustion processes of.

3.1.2 Second-order sensitivity analysis

Pairs of reactions that have the largest correlated effect on ignition delay times with GSA and LSA are illustrated in Fig.2.Results of GSA and LSA are again quite similar to each other.One can see from this figure that correlated effect of the two chain branching reaction:No.16 (H + O2= OH + O) and No.15(O+ H2= OH + H) are the most important reaction pair on ignition delay time at high temperature and normal pressure condition,i.e.,T = 1400 K,p = 1 Pa.On the other hand,reaction No.16 (H + O2= OH + O) and No.9 (H + O2(+M) = HO2(+M)) are the most important reaction pair on ignition delay time under the other conditions.First-order sensitivity coefficients of reactions No.9 and 16 are the largest under the conditions of T= 1000 K,p = 1 Pa,φ = 1.0 and T = 1400 K,p = 40 Pa,φ = 1.0,while they are the third and fourth most important reactions with T = 1000 K,p = 40 Pa,φ = 1.0,according to our first-order sensitivity analysis.On the other hand,reactions Nos.15 and 16 are the most important two reactions under the condition of T =1400 K,p = 1 Pa,φ = 1.0.This seems to indicate that correlated effect of two reactions is important when the two reactions also have large first-order sensitivity coefficient.However,reaction No.22 (H + HO2= H2+ O2) and reaction No.16 (H + O2= OH+ O) have sizable correlated effect on ignition delay time under the condition of T = 1000 K,p = 40 Pa,φ = 1.0,while reaction No.22 does not have a pronounced effect on ignition delay time under this condition.This shows it is possible that correlated effect of an important reaction and a minor reaction could still be important on ignition delay time.

Fig.1 First-order global and local sensitivity coefficients of important reaction on ignition delay time of H2.

3.2 Sensitivity analysis on ignition delay time of methane

The GRI-Mech 3.0 mechanism is one of the most popular reaction mechanisms for combustion of methane and it contains 53 species and 325 reactions.Number of model runs is too large if first- and second-order sensitivity analysis are carried out for all the involved reactions even with the present approach.Skeletal mechanism reduction is performed before mechanism analysis.A skeletal mechanism is obtained based on intersection50of skeletal mechanisms obtained from direct relation graph(DRG)51–53,DRG with error propagation (DRGEP)54,revised DRG approach55,path flux analysis(PFA)56,and flux projection tree method (FPT)57approaches over range of temperature of 1000–1600 K,pressures of 1–20 Pa,and equivalence ratios of 0.5–1.5.The skeletal mechanism employed in sensitivity analysis contains 22 species and 109 reactions with a maximum error of 10.5% on ignition delay times compared with the detailed mechanism on these conditions.In addition,computational cost can be reduced when the skeletal mechanism is employed in simulation of ignition delay time compared with that using the detailed mechanism,particularly when a large number of model runs are required in sensitivity analysis.Firstand second order sensitivity coefficients of the 109 reactions in the skeletal mechanism are calculated for ignition delay times in a zero-dimensional closed homogeneous reactor with constant pressure under the initial condition of T = 1000 K,p = 1 Pa,φ =1.0;T = 1000 K,p = 20 Pa,φ = 1.0;T = 1400 K,p = 1 Pa,φ =1.0;and T = 1400 K,p = 20 Pa,φ = 1.0,respectively.

Fig.2 Second-order global and local sensitivity coefficients of important pairs of reactions on ignition delay time of H2.

3.2.1 First-order sensitivity coefficients

Reactions that have the largest absolute sensitivity coefficients on ignition delay time under the four conditions in GSA and LSA are illustrated in Fig.3.It can be seen that important reactions identified with GSA are consistent with those using LSA in most cases.In fact,all the four methods,i.e.,GSA,GSA-1,LSA and LSA-1,provide quite similar information on important reactions in most cases except for the case of T = 1400 K and p = 20 Pa.Reaction No.93 CH3+ H2O2=HO2+ CH4,is the second most important reaction on ignition delay time at T = 1400 K and p = 20 Pa with GSA.However,effect of this reaction on ignition delay time at this condition is calculated to be unimportant with the other three approaches.Results of GSA depend on how the orthonormal polynomials are chosen,while LSA does not have such a problem.Difference between GSA and GSA-1 arises from the second-order term mathematically.In addition,the input parameters are allowed to vary in a relatively small range,which means generally LSA and GSA should not differ too much.The fact that the other three approaches give similar results indicates that GSA may overestimate importance of this reaction.

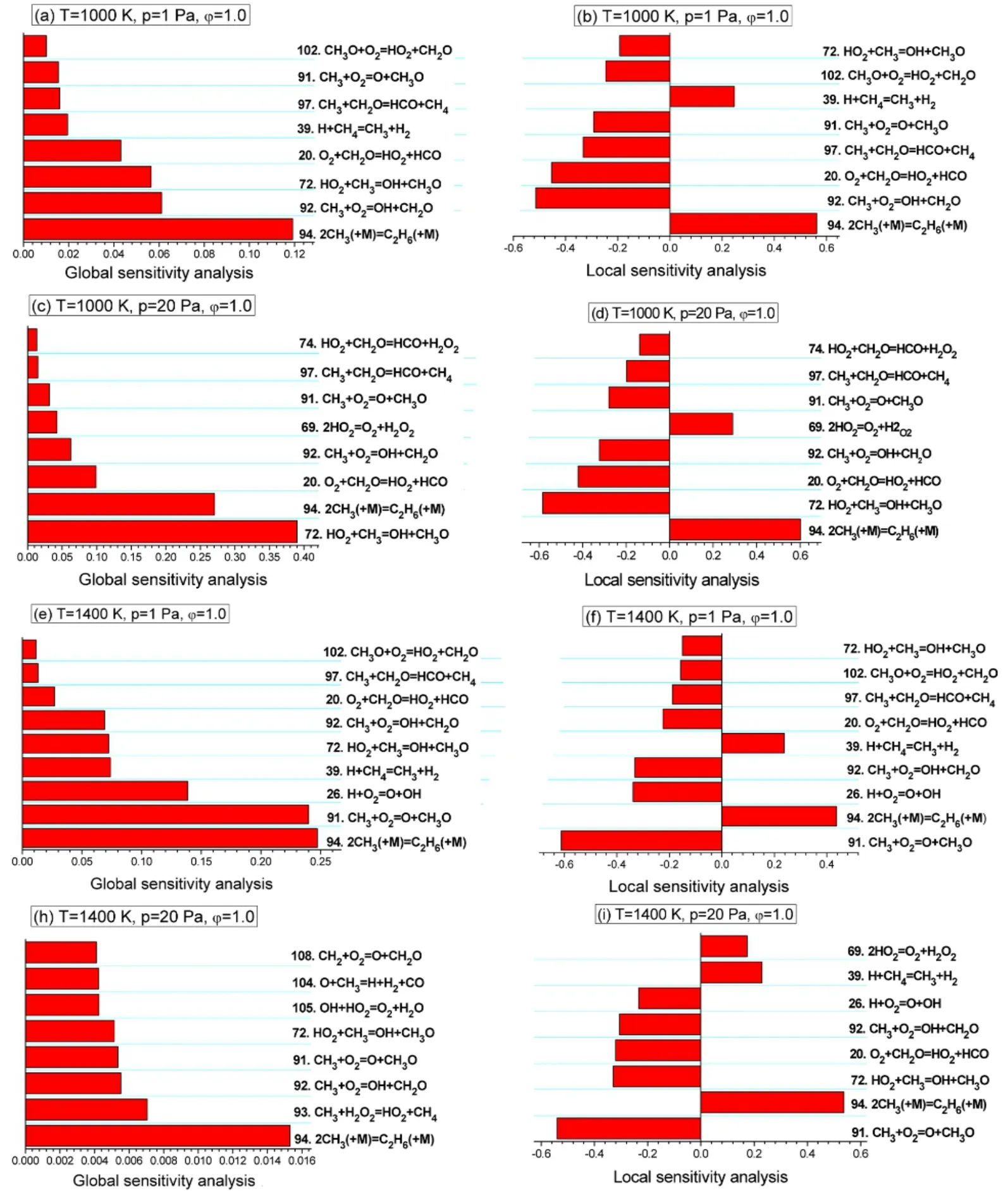
Fig.3 First-order global and local sensitivity coefficients of important reaction on ignition delay time of CH4.

According to results in Fig.3,the recombination reaction 2CH3(+ M) = C2H6(+ M) is always an important reaction on ignition delay times of CH4under all the considered conditions.One can see from LSA results that this recombination reaction suppresses ignition due to annihilation of radicals.On the other hand,global sensitivity coefficients are always positive and it is not straightforward to tell whether the reaction actually promotes or suppresses ignition only with global sensitivity coefficients.Reaction No.72:HO2+ CH3= OH + CH3O becomes more important to promote ignition at higher pressures.On the other hand,CH3+ O2= OH + CH2O is rather important on ignition at 1000 K and 1 Pa,while reaction CH3+ O2= O + CH3O becomes more important at 1400 K and 1 Pa.

3.2.2 Second-order sensitivity coefficients

Pairs of reactions that have important correlated effect on ignition delay time of methane using GSA and LSA are illustrated in Fig.4.It can be seen from this figure that second-order sensitivity coefficients of many pairs of reactions are quite similar.This is particularly the case for ignition delay time at T = 1400 K and p = 20 Pa.It is thus difficult to figure out certain pairs of reactions that have significantly more important correlated effects on ignition delay time than the other pairs.An interesting observation is that the pairs of reactions that have the largest second-order global sensitivity coefficients always contain reaction No.94 at T = 1400 K and p = 20 Pa in GSA,which also has the largest first-order global sensitivity coefficient at this condition.

Fig.4 Second-order global and local sensitivity coefficients of important pairs of reactions on ignition delay time of CH4.

In most cases the pairs of reactions that are important on ignition delay time using GSA are also identified as important reaction pairs with LSA,although the sequence of the absolute second-order sensitivity coefficients with GSA may be different from that using LSA.The pairs of reactions that are important on ignition delay times are usually composed of reactions that have large first-order sensitivity coefficients.However,reaction pair of No.71 HO2+ CH3= O2+ CH4and No.72 HO2+ CH3= OH +CH3O are shown to have large correlated effect on ignition delay time at T = 1000 K,although reaction No.71 has only a rather small first-order sensitivity coefficient.lnτ at T = 1000 K and p =1 Pa at different scaling factor for reaction No.71 is plotted in Fig.5a and it can be seen that ignition delay time does not change monotonically with respect to the scaling factor.To further investigate sensitivity of reaction No.71 on ignition delay time,we treat the forward and backward reactions for HO2+ CH3=O2+ CH4as two irreversible reactions and only the forward or the backward reaction is scaled in simulation of ignition delay time.The obtained ignition delay times at the temperature of 1000 K and pressure of 20 Pa with respect to the scaling factor for the forward and the backward reactions are plotted in Fig.5b,c,respectively.We can see that the forward reaction suppresses ignition,while the backward reaction actually promotes ignition.First-order sensitivity analysis is also carried out by treating the forward and backward reactions as two irreversible reactions.We found that these two reactions have sizeable first-order sensitivity coefficients.This can explain that this reaction and another important reaction could possibly have pronounced correlated effect on ignition delay time.This seems to imply that reversible reactions have better be treated as two irreversible reactions in sensitivity analysis.However,the forward reaction rate constant and the backward reaction rate constant are connected by the equilibrium constant.If uncertainty of the equilibrium constant is quite small or if we are not interested in sensitivity of thermodynamic parameters,it is reasonable to treat reversible reaction as a single reaction in sensitivity analysis.

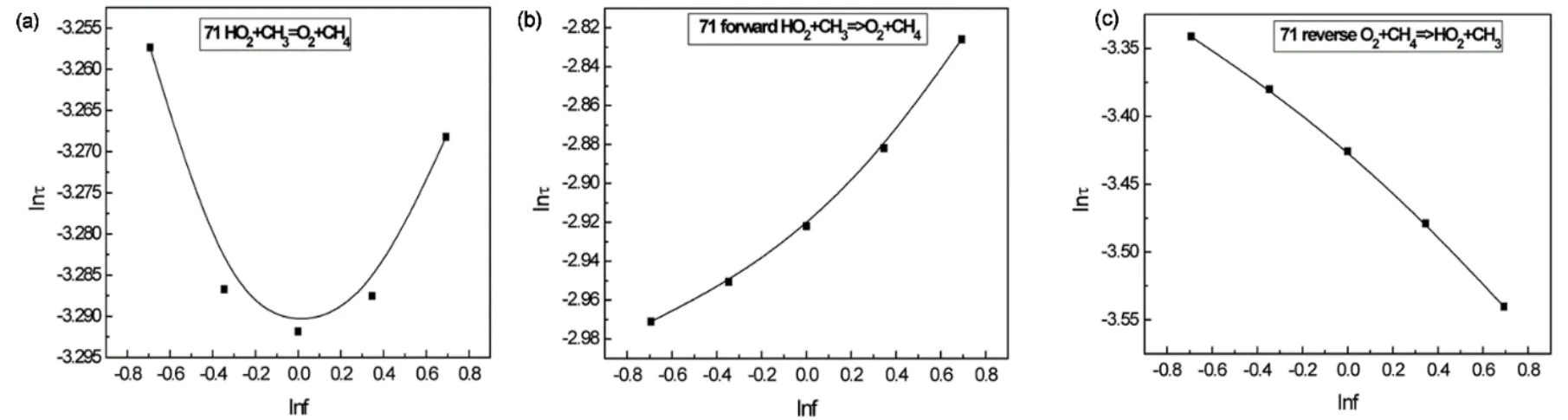
Fig.5 Ignition delay time versus scaling factor for rate constant of reaction No.71 in reaction mechanism of methane at T = 1000 K and p = 20 Pa.

Fig.6 First-order global and local sensitivity coefficients of important reaction on ignition delay time of n-butane.

3.3 Sensitivity analysis on ignition delay time of nbutane

The detailed reaction mechanism for combustion of n-butane58containing 230 species and 1328 reactions is reduced before sensitivity analysis.A large number of model runs are required to perform sensitivity analysis and it will be too demanding to use the detailed mechanisms in the model runs.We thus choose to carry out sensitivity analysis using skeletal mechanisms derived from these detailed mechanisms.FPT is employed for mechanism reduction over range of temperature of 600–1600 K,pressures of 1 Pa,and equivalence ratios of 1.0.The resulting skeletal mechanism contains 80 species and 420 reactions and the largest relative error on ignition delay time with the skeletal mechanism is 8.8%,which is able to provide a reliable description on combustion of this fuel.It is still rather demanding to carry out sensitivity analysis on all the reactions in the skeletal mechanism.The 100 reactions with the largest absolute first-order local sensitivity coefficients from traditional local sensitivity analysis are chosen for global and local sensitivity analysis under the initial conditions of T = 650 K,p =1 Pa,φ = 1.0;T = 1000 K,p = 1 Pa,φ = 1.0;and T = 1400 K,p= 1 Pa,φ = 1.0.It should be noted that only about 20–30 reactions are chosen in global sensitivity analysis with RSHDMR.The 100 reactions under one initial condition is different from those under another initial condition.

Fig.7 Second-order global and local sensitivity coefficients of important pairs of reactions on ignition delay time of n-butane.

The reactions with the largest absolute first-order sensitivity coefficients on ignition delay time at T = 650 K,1000 K and 1400 K according to GSA and LSA are listed in Fig.6.According to this figure,important reactions with these four sensitivity analysis methods are quite similar to each other.At low temperature,decomposition of H2O2to form OH and H-abstraction reaction of the fuel by OH are the most important two reactions that promote ignition.Reactions involving C4H9OO and C4H8OOH also play an important role in ignition at this temperature.On the other hand,two reactions between CH3and HO2have the largest effect on ignition delay time at 1000 K.Recombination of the two radicals CH3and HO2to produce stable molecules CH4and O2suppress ignition,while reaction between these two radicals to produce CH3O and OH is the most important reaction that promote ignition at this temperature.One can see from this figure that a bunch of reactions have similar absolute sensitivity coefficients on ignition delay time at low temperature,while the chain branching reaction H + O2= OH +O has significantly larger absolute sensitivity coefficients than the other reactions at high temperature.

The pairs of reactions that have important correlated effects on ignition delay times of n-butane at T = 650 K,1000 K and 1400 K,respectively,according to GSA and LSA are displayed in Fig.7.One can see from this figure that the four pairs of reactions that affect ignition delay time at T = 650 K the most according to GSA all contain reaction No.294:C4H10+ OH =pC4H9+ H2O.This reaction also has the largest absolute firstorder sensitivity on ignition delay time at this temperature.Furthermore,most of the important reaction pairs for ignition delay time at 650 K are composed of two reactions that have large first-order sensitivity coefficients.On the other hand,correlated effect between reaction No.16:H2O2(+M) =2OH(+M) and another reaction is minor although this reaction ranks No.2 and No.1 in first order GSA and LSA,respectively.The most important reaction pair on ignition delay time at 1000 K is reaction no.16 H2O2(+M) = 2OH(+M) and reaction No.294:C4H10+ OH = pC4H9+ H2O.First-order sensitivity coefficients of these two reactions rank Nos.5 and 6 in GSA,respectively.At high temperature,the chain branching reaction H + O2= OH + O together with another reaction have important correlated effect on ignition delay time.In fact,H + O2= OH +O and reaction No.128:C2H4+ H(+M) = C2H5(+M) are the most important reaction pair on ignition delay time according to our results,although reaction No.128 has a rather small first-order sensitivity coefficient.Its first-order sensitivity coefficient ranks No.21 in GSA and 23 in LSA.

Fig.8 First-order global and local sensitivity coefficients of important reaction on ignition delay time of n-heptane.

3.4 Sensitivity analysis on ignition delay time of nheptane

The detailed mechanism for combustion of n-heptane59,60employed in this work contains 561 species and 2539 reactions.A skeletal mechanism based on intersection of skeletal mechanisms obtained from DRG,DRGEP and FPT over the range of temperature of 600–1800 K,pressures of 1–40 Pa,and equivalence ratios of 0.5–1.5 is adopted in sensitivity analysis.The skeletal mechanism is composed of 175 species and 799 reactions and the maximum error on ignition delay times of these conditions is 11%.We calculated first and second-order global and local sensitivity coefficients of the 80 reactions with the largest first-order local sensitivity coefficients on ignition delay times under the initial conditions of T = 650 K,p = 1 Pa,φ = 1.0;T = 1000 K,p = 1 Pa,φ = 1.0;and T = 1400 K,p = 1 Pa,φ = 1.0.

Reactions with the largest absolute first-order sensitivity coefficients from GSA and LSA are illustrated in Fig.8.Reactions that have significant effect on ignition delay times at these conditions according to GSA are also shown to be important with LSA for combustion of n-heptane.Our results show that the chain termination reaction:HO2+ OH = H2O + O2has the largest effect to suppress ignition at low temperature.On the other hand,decomposition of H2O2to produces OH is the most important reaction that promotes ignition and this reaction also has large sensitivity coefficient on ignition delay time of nbutane at low temperature.However,sensitivity coefficients for reactions involving peroxyl radical of n -heptane are not very large compared with those of the listed reactions.Reactions involving ROO such as the C7H15O2–2= C7H14OOH2–4ranked 8th and 12th respectively in the global and local sensitivity analysis.On the other hand,sensitivity coefficient of reaction O2QOOH = keto-hydroperoxide + OH ranks around 20th.It is well-known that reactions involving ROO and O2QOOH play an important role in low temperature ignition of alkanes.C7H15OO has several isomers that undergo similar reactions.Sensitivity coefficient for any single reaction involving ROO or O2QOOH is not among the largest ones,but combinational effect of reactions involving isomers of ROO could still be significant.At intermediate temperature,decomposition reaction of H2O2still plays an important role on ignition.Similar to the case of ignition of n-butane at 1000 K,the two reactions between CH3and HO2are rather important on ignition delay time of n-heptane.At high temperature,absolute sensitivity coefficient of the chain branch reaction:H + O2= OH + O are much larger than that of the other reactions.

Pairs of reactions that have the largest absolute second-order sensitivity coefficients on ignition delay times are listed in Fig.9.It can be seen from this figure that reactions involving nheptane are rather important in second-order sensitivity analysis for ignition at 650 K,while they are less important in first-order sensitivity analysis at this temperature.On the other hand,the most important pairs of reactions usually contain reactions related to CH3at intermediate temperature.At 1400 K,reaction No.8 H+O2= OH + O always appear in the pairs of reactions that have the largest absolute second-order sensitivity coefficients.In addition,first-order sensitivity coefficient of reaction No.564 n-C7H16+ H = C7H15-3+ H2is quite small,but this reaction together with reaction No.8 constitute the reaction pair that has the largest second-order sensitivity coefficient at 1400 K.

Fig.9 Second-order global and local sensitivity coefficients of important pairs of reactions on ignition delay time of n-heptane.

4 Conclusions

We propose to calculate both first- and second-order global and local sensitivity coefficients of ignition delay time with respect to reaction rate constants of H2,methane,n-butane and n-heptane at various conditions in this work.Ignition delay time with respect to the factors that scale reaction rate constants is expanded using a normal polynomial function with at most coupling between two reactions.The polynomial function is determined from ignition delay times by scaling rate constants of one and two reactions and both global and local sensitivity coefficients are determined from this polynomial function.Number of samples required to determine global sensitivity coefficients can be reduced compared with global sensitivity analysis using RS-HDMR.In RS-HDMR,sensitivity coefficients are determined for rate constants of a limited number of reactions,while the present approach is able to afford sensitivity coefficients for a larger number of reactions.

Reactions and reaction pairs with the largest sensitivity coefficients are listed for ignition delay time of these four fuels.The factor that scale reaction rate constants vary in a small range and important reactions or reaction pairs identified with global sensitivity analysis are usually the same as those from local sensitivity analysis.This is probably because nonlinear effect is still unimportant in this small range of parameters.It is possible to determine global sensitivity coefficients by varying the input parameters in a larger range using the present approach.Our results show that correlated effects between an important reaction and a minor reaction could also have significant secondorder sensitivity coefficient in some cases.On the other hand,first-order global sensitivity coefficients with the present approach will be affected by coupling between two reactions and occasionally some result with first-order global sensitivity analysis will be different from those with local sensitivity analysis or global sensitivity analysis by neglecting the correlated effects of two reactions.The present sensitivity analysis approach can provide valuable information on important reactions as well as correlated effects of two reactions reaction on combustion characters obtained from chemical kinetic mechanisms of combustion.Furthermore,it can also be employed to aid global sensitivity analysis using RS-HDMR where global sensitivity coefficients are determined more reliably.