圆环巴西试验的抗拉强度建议公式

王杰，陶俊林，郭辉



圆环巴西试验的抗拉强度建议公式

王杰，陶俊林，郭辉

（西南科技大学 土木工程与建筑学院，四川 绵阳 621010）

改进Hobbs公式得到的计算值普遍较大这一问题，提出圆环巴西试验的抗拉强度建议公式。对巴西试验圆环的应力解进行分析，并引用砂岩的试验数据验证。得到圆环巴西试验的抗拉强度建议公式，使用Hobbs公式得到的抗拉强度TT比巴西圆盘试验T大6倍以上，利用建议公式得到的抗拉强度σ与巴西圆盘试验T十分接近，误差不到1%。当圆环内外径比在0.05到0.15的范围内时，该建议公式可很好地用来计算岩石类等脆性材料的抗拉强度。

圆环试件；劈拉试验；抗拉强度公式

巴西圆盘试验广泛应用于间接测量岩石、混凝土等脆性材料的抗拉强度，得到了相关规程的推荐[1-2]。巴西圆盘试验有时会出现在加载点处起裂的情况[3]，这属于受压破坏，不易满足巴西圆盘试验的起裂条件。由此，Hobbs D W[4]提出在试件中心钻一个贯穿的圆孔，形成圆环试件，使试件从内孔开始起裂，来保证试件受拉破坏，并提出该方法的抗拉强度计算公式（Hobbs公式）。

随后，学者们引用Hobbs公式对脆性材料的抗拉强度做了大量的研究[5-11]。尤明庆等[5]对片麻岩、大理岩等材料做了圆环巴西试验，认为当圆环试件内外径比小于0.4时，用Hobbs公式得到的拉伸强度远大于巴西圆盘试验强度，得出Hobbs公式不能作为岩石抗拉强度公式的结论[6-7]。文献[8-11]对圆环巴西试验做了数值模拟。朱万成等[8]认为，如果能准确测出圆环试件的开裂载荷，可将Hobbs公式中的载荷峰值替换为开裂载荷，这时计算出的抗拉强度较为符合。要准确获得试验的开裂载荷，现在的实验手段不易达到。

为此，文中对巴西试验圆环的应力解析解进行分析，提出圆环巴西试件的抗拉强度建议公式。在圆环内外径比较小时，其计算值可表示岩石类脆性材料的抗拉强度。

1 抗拉强度公式介绍

1.1 巴西圆盘试验强度计算公式

在巴西圆盘试验中，加载线上的拉应力是常值2/π；在圆盘的中心处，拉应力是压应力的1/3。根据岩石、混凝土等脆性材料受压不受拉的特点，可得出巴西圆盘拉伸强度公式[1]：

式中：为施加在圆盘试件上的载荷峰值；为圆盘直径；为圆盘试件厚度。

1.2 圆环巴西试验强度计算公式

Hobbs D W[4]提出圆环巴西试验抗拉强度计算公式：

式中：为施加在圆环试件上的载荷峰值；为圆环试件的厚度；和分别为圆环试件的内半径和外半径。

式（2）是中心孔与=0直线的交点（如图1所示）的环向正应力近似表达，使用该公式的前提是：当内环边界上点的环向正应力达到了材料的抗拉强度时，圆环试件的承载能力达到最大值。当点出现裂纹后（点处的环向正应力达到了材料的抗拉强度），这时的试件往往还能承载，承载力还会继续增大。因此，点出现裂纹，并不意味着试件的承载能力完全丧失。这是公式（2）用载荷峰值计算出的抗拉强度较高的可能原因。

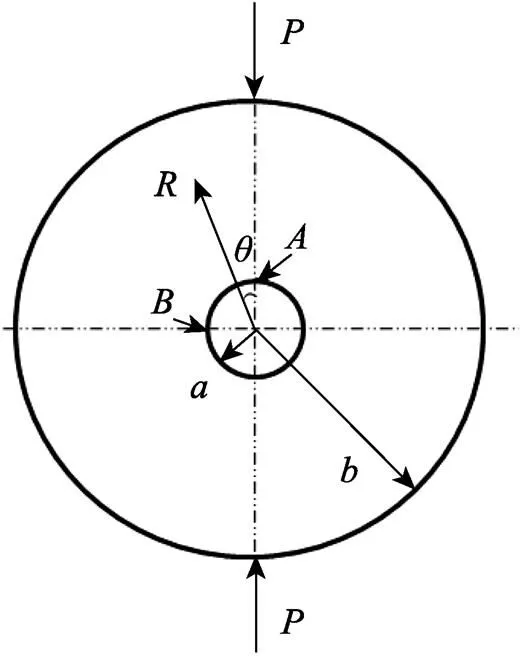
图1 巴西试验圆环

2 圆环巴西试验建议公式的提出

Chianese R B等[12]以弹性力学叠加原理和平面应力状态为基础，利用傅里叶级数推导出巴西试验圆环的应力表达式：

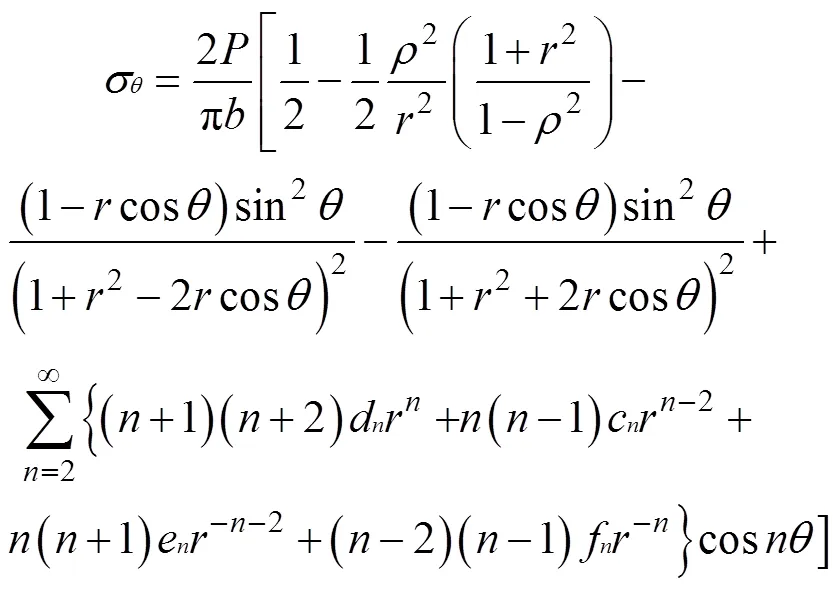
其中：

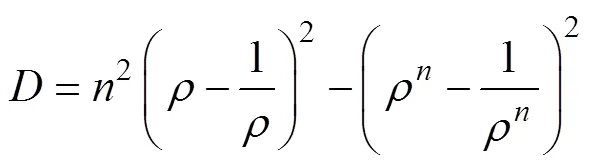
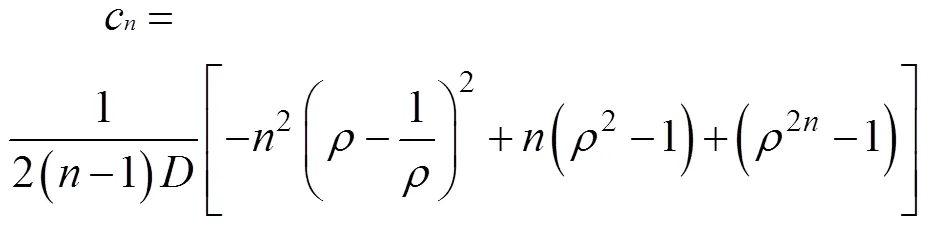
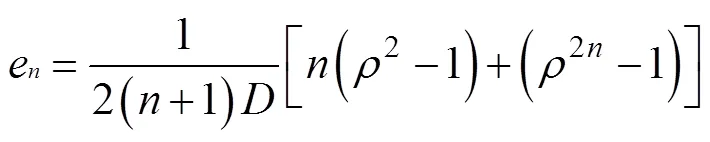
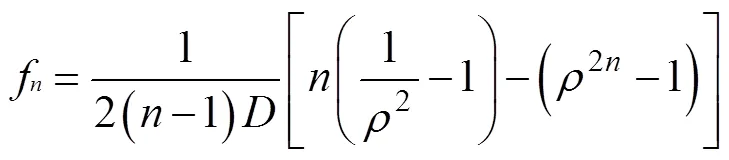
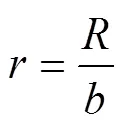
式中：为非零偶数。式中的相关参数如图1所示。

根据公式（4），可得出不同内外径比下的内环边界环向正应力曲线，如图2所示。由于边界条件是轴对称的，只画出了弧部分（如图1所示）。

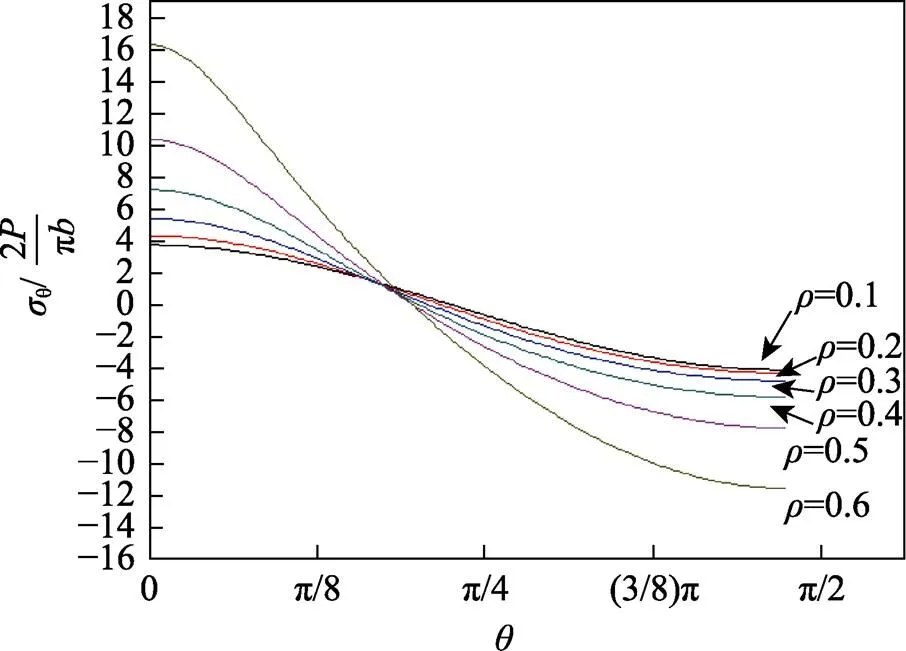
图2 弧上各点的环向正应力

对同一条曲线，环向正应力由正值向负值转换，最大拉应力值在=0处（图1的点），而最大拉应力值与最大压应力值不相上下。这说明由岩石、混凝土等脆性材料制成的环形试件会从点起裂，即受拉破坏。不同下也有类似的规律（大于0.6也是如此），说明值大小对圆环试件从点起裂并无影响。

为了了解圆环在=0直线上的拉压状态，利用式（4），画出=0直线上的环向正应力变化曲线，如图3所示。

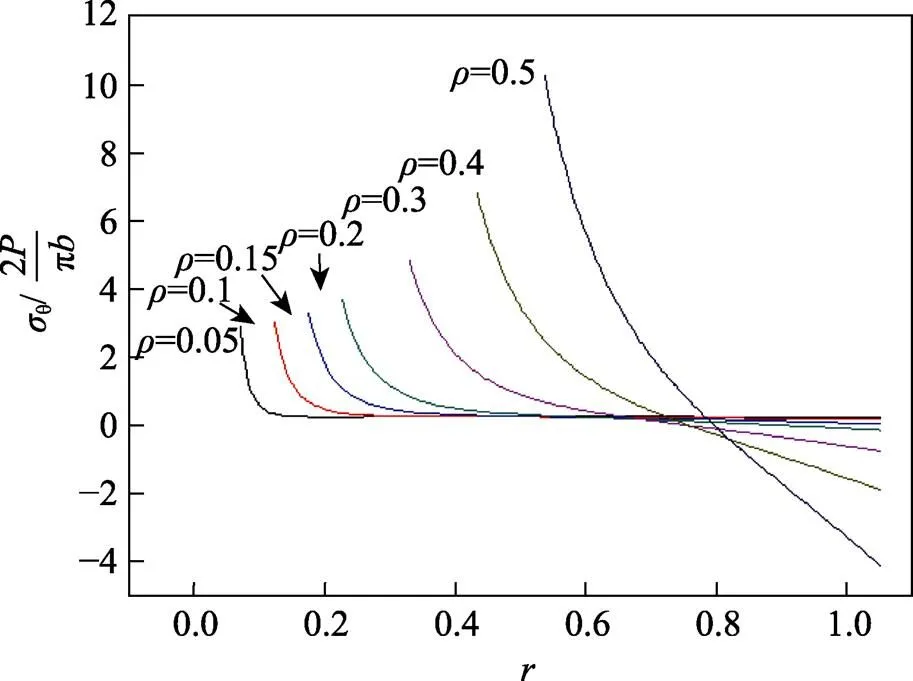
图3 θ=0直线上的环向正应力

由图3可知，当=0.5时，=0直线上的环向正应力快速下降。随着的减小，这种趋势发生了改变，“下降区”逐渐变短，在远离中心孔的部分逐渐形成一段平台；尤其在≤0.15时，这种趋势越加明显。这段长平台的形成，意味着=0直线上绝大部分的环向正应力是几乎相等的。对于≤0.15的脆性材料试件，点会最先达到脆性材料的抗拉强度，发生拉伸破坏。当载荷继续增加时，裂纹才会延展，而当裂纹延伸到“长平台区”时，由于“长平台区”的环向正应力几乎相等，这时脆性材料同时发生破坏。若“长平台区”主导着脆性材料的拉伸破坏，则可在“长平台区”内取一点来表示脆性材料的拉伸强度。

下面对圆环试件的拉伸破坏由“下降区”主导，还是由“长平台区”主导进行讨论，以=0.05曲线为例，如图4所示。

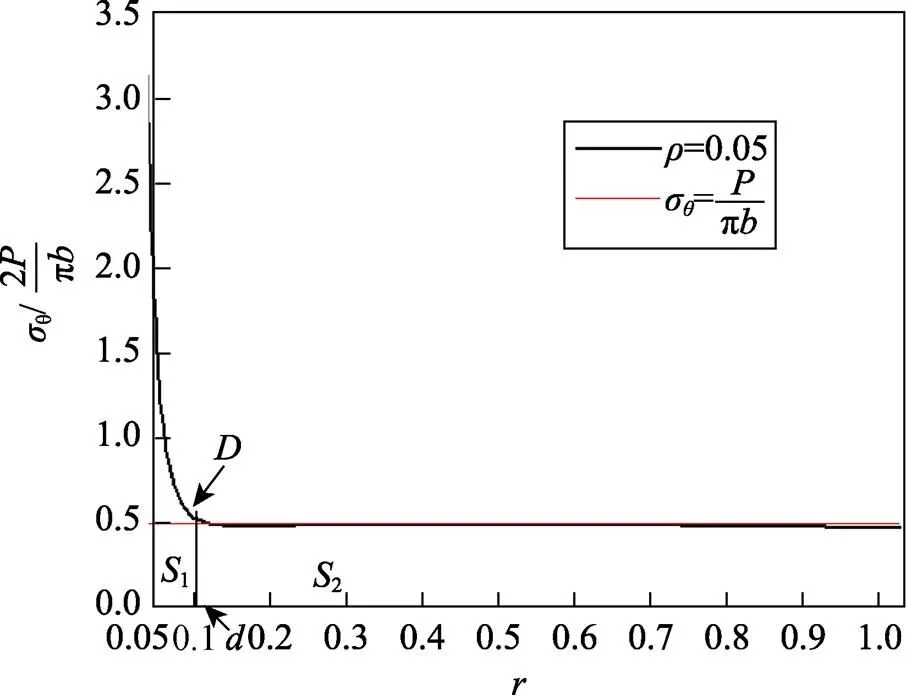
图4 ρ=0.05时在θ=0直线上的环向正应力

将图4中的=0.05曲线的“长平台区”线性拟合，得到拟合曲线的表达式：

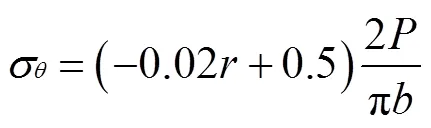
由于式（12）中，含项的系数十分小，对式（12）的变化趋势基本无影响，为了化简表达式，将公式（12）简化为：

利用上述方法计算不同时的1、2值。为了便于比较，在表1中列出不同时的1、2值。

表1 不同内外径比ρ时的S1、S2值

在表1中，内外径比在0.05~0.15的范围内，1<2，即“下降区”面积小于“长平台区”面积。这说明对于内外径比在0.05~0.15的圆环巴西试验，其拉伸破坏由“长平台区”主导。又由于“长平台区”段曲线与横坐标基本平行，即该段的环向正应力十分接近，则可在图3中公有的“长平台区”内取一点来表示脆性材料的抗拉强度。如图3所示，可取=0.5时的环向正应力来表示脆性材料的抗拉强度公式，将=0.5、=0代入式（4）中，并考虑试件厚度，得到表达式：

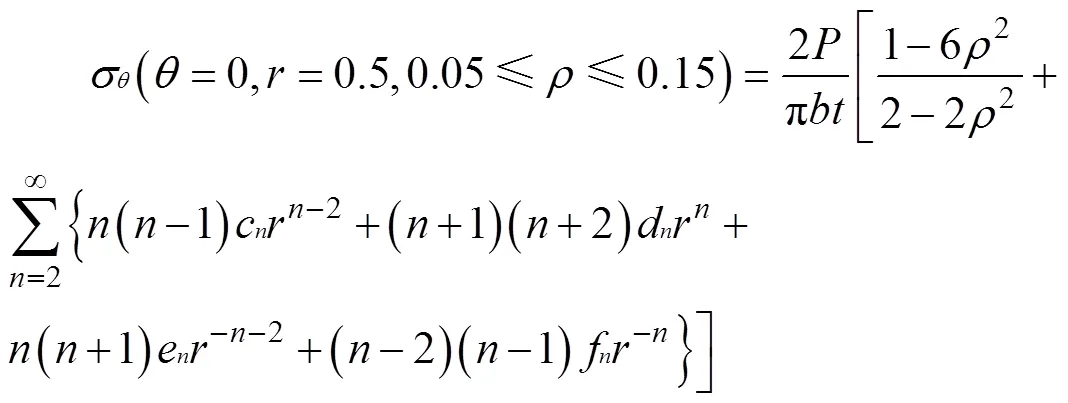
式（14）是脆性材料的建议抗拉强度计算公式，由于其存在多项式，使得表达式十分复杂，且随着的增加而逐渐收敛。在图5中给出了不同值时公式（14）的收敛情况。

在图5中，“=10”曲线和“=20”曲线完全重合，说明当=10时，式（14）已经收敛了。此时的式（14）仍然十分复杂，不易运用。为了化简公式，将=10时的式（14）进行三次多项式拟合，拟合情况如图6所示。

在图6中，三次多项式拟合曲线与“=10时的式（14）”曲线十分接近，其标准方差达到了99.7%。

图5 不同n值时式（14）的收敛情况

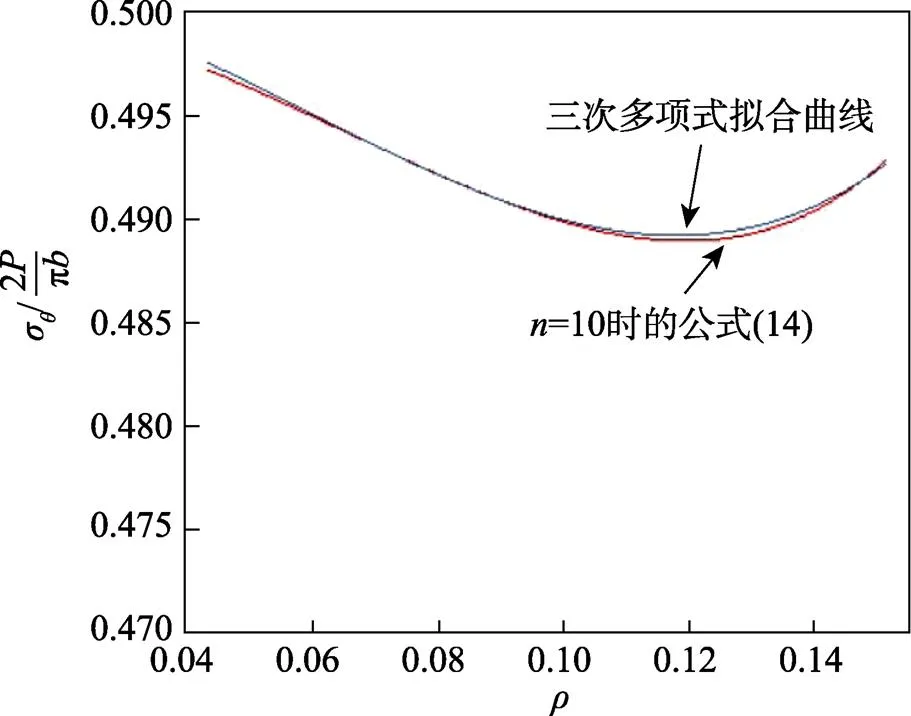
图6 n=10时式（14）的三次多项式拟合

为了化简强度公式，便于推广应用，式（14）可用三次多项式拟合曲线表达式替代，可简化为：

3 圆环巴西试验建议公式的验证

选用文献[7]表格2中砂岩的劈拉试验数据对建议公式进行验证。砂岩试件为圆柱体，直径均为50 mm，其高度和内孔直径见表2。利用式（1）、（2）和（15）分别得到强度值T、TT和σ。

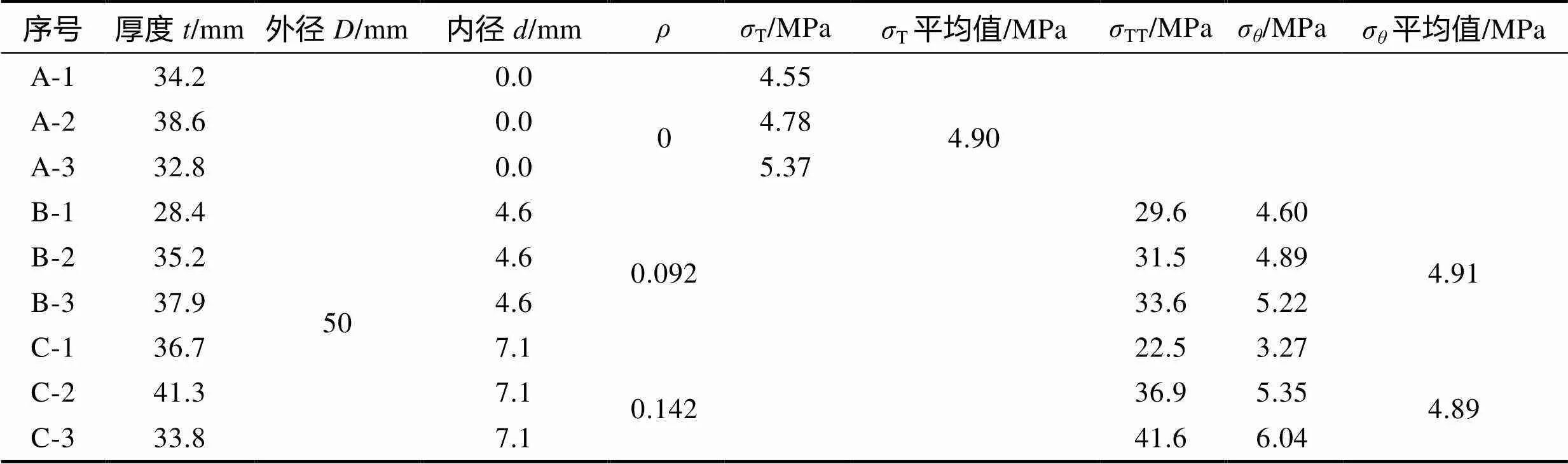
表2 不同内外径比ρ时的σT、σTT和σθ值对比

注：=0时，试件是实心圆柱体，为巴西圆盘试验

巴西圆盘试验广泛应用于测量脆性材料的抗拉强度，因此，文中将TT、σ与T作对比。在表2中，TT值比T平均值大6倍以上，两者相差太大，TT值不宜作为脆性材料的抗拉强度值；当=0.092时，σ平均值与T平均值十分接近，误差不到1%；当=0.142时，σ平均值与T平均值也十分接近，误差不到1%。由此说明，对于圆环巴西试验，使用建议公式（15）计算岩石类脆性材料的抗拉强度是可行的。

4 结语

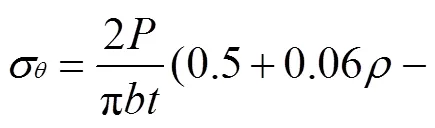
[1] MOHAMMAD D, FERAS F, HANI A, et al. Suggested Methods for Determining Tensile Strength of Rock Materials[J]. International Journal of Rock Mechanics & Mining Science & Geomechanics Abstracts, 1978, 15(15): 99-103.

[2] SL 264—2001, 水利水电工程岩石试验规程[S].

[3] HUDSON J A, BROWN E T, RUMMEL F. The Controlled Failure of Rock Discs and Rings Loaded in Diametral Compression[J]. International Journal of Rock Mechanics & Mining Sciences & Geomechanics Abstracts, 1972, 9(2): 241-248.

[4] HOBBS D W. An Assessment of a Technique for Determining the Tensile Strength of Rock[J]. British Journal of Applied Physics, 2002, 16(2): 259.

[5] 尤明庆, 陈向雷, 苏承东. 干燥及饱水岩石圆盘和圆环的巴西劈裂强度[J]. 岩石力学与工程学报, 2011, 30(3): 464-472.

[6] DI-YUAN L I, WANG T, CHENG T J, et al. Static and Dynamic Tensile Failure Characteristics of Rock Based on Splitting Test of Circular Ring[J]. Transactions of Nonferrous Metals Society of China, 2016, 26(7): 1912-1918.

[7] 尤明庆, 苏承东. 砂岩孔道试样压拉应力下强度和破坏的研究[J]. 岩石力学与工程学报, 2010, 29(6): 1096-1105.

[8] 朱万成, 冯丹, 周锦添, 等. 圆环试样用于岩石间接拉伸强度测试的数值试验[J]. 东北大学学报(自然科学版), 2004, 25(9): 899-902.

[9] 王来贵, 赵娜, 周永发. 岩石圆环试件拉张破裂结构演化有限元模拟[J]. 自然科学进展, 2009, 19(4): 467-472.

[10] LIU K, LIU B, LIU W. Numerical Study on Size Effect of Ring Specimen under Brazilian Test[C]// International Young Scholars' Symposium on Rock Mechanics. [s. l.]: [s. n.], 2008.

[11] 刘文彬, 唐春安, 张后全. 圆环试样内径对抗拉强度的影响[J]. 岩土工程技术, 2004, 18(6): 286-290.

[12] CHIANESE R B, ERDLAC R J. The General Solution to the Distribution of Stresses in a Circular Ring Compressed by Two Forces Acting Along a Diameter[J]. The Quarterly Journal of Mechanics and Applied Mathematics, 1988, 41(2): 239-247.

Proposed Formula for Tensile Strength of Ring Brazil Test

WANG Jie, TAO Jun-lin, GUO Hui

(School of Civil Engineering and Architecture, Southwest University of Science and Technology, Mianyang 621010, China)

To propose a formula for the tensile strength of the ring Brazil test and eliminate the problem that the calculated values obtained by the Hobbs formula are generally larger.The stress solution of the Brazilian test ring was analyzed and the sandstone experiment data for verification was cited.The proposed formula of the tensile strength of the ring Brazil test was obtained; the tensile strength obtained through the Hobbs formula was six times more than that of the Brazilian disc test; and the tensile strength obtained through the proposed formula was very close to the Brazilian disc test with an error of less than 1%.The proposed formula can be used to calculate the tensile strength of brittle materials when the inner and outer diameter ratioof the ring specimen is in the range of 0.05 to 0.15.

ring specimen; splitting test; tensile strength formula

10.7643/ issn.1672-9242.2019.02.009

TB122

A

1672-9242(2019)02-0042-05

2018-10-17；

2018-11-17

王杰（1994—），男，重庆人，硕士研究生，主要研究方向为脆性材料劈拉力学性能。

陶俊林（1972—），男，四川人，博士，教授，主要研究方向为材料和结构的力学行为。