液体火箭发动机振动故障特征信号提取方法

2019-03-08刘英元陈海峰朱成亮

火箭推进 2019年1期

刘英元，陈海峰，耿直，朱成亮

(西安航天动力试验技术研究所，陕西西安 710100)

0 引言

在液体火箭发动机试验中各种因素对故障诊断都会产生影响，这种影响会以振动信号特征值的形式表现出来。

在对随机振动信号进行时频分析时，由于所测取的振动信号不但包含故障信号, 而且还包含其发动机工作时的振动信号, 并且在早期的故障产生阶段, 其故障特征信息很微弱, 信噪比很小, 有用的特征信号往往淹没在发动机其他部件运行中引起的振动信号和大量的随机振动信号中, 如何提取特征信号是进行振动信号故障诊断的重要问题。

1 故障诊断的数学模型

对于通常的发动机故障诊断问题，在数学模型上可以将该发动机作为一个整体系统，通过检测反映系统异常工作状态的信息来判定发动机是否发生故障，这些信息可用如下的模型表示[1]：

Y=f(U,X,θ)

(1)

式中：Y为振动信号；U为振源；X为振动过程中的状态量；θ为这一模型中的其余影响参数。

在上述机械故障诊断系统数学模型中，主要的模型有：

(ARMAI):A(q-1)y(t)=
B(q-1)u(t)+C(q-1)e(t)

(2)

(ARMA):A(q-1)y(t)=C(q-1)e(t)

(3)

(ARMAIP):A(q-1,P)y(t)=
B(q-1,P)u(t)+C(q-1,P)e(t)

(4)

(ARMAP):A(q-1,P)y(t)=
C(q-1,P)e(t)

(5)

(PLI):y(t)=C0+C1u(t)+C2u(t)+…

(6)

(PL):y(t)=C0+C1e(t)+C2e(t)+…

(7)

(NL):y(t)=NL(u(t))

(8)

式中：ARMAI为数据输入模型；ARMA为时序模型；e(t)为不可测输入量；q-1为单位滞后算子，这一模型包括了AR和MA模型；ARMAIP和ARMAP为非线性模型；PLI和PL为多项式模型；NL为神经元网络模型；u(t)为离散随机过程。A，B和C多项式的每一个系数都是P的非线性函数，满足：

A(q-1,P)=1+a1(P)q-1+
a2(P)q-2+…+an(P)q-n

(9)

对于机械发动机的某一个子系统，每一个测量量或是每一组测量量都可用一个模型表示，因而一个系统可用如下的一组模型表示：

S={y1，u1，f1;y2,u2,f2;…；ym,um,fm}

(10)

因此，在整个故障诊断过程中，无非是从S出发，经过特定的算法得出S的变化量C(特征向量)，该特征向量可表示为:

C={Δy1,Δe1,Δx1,Δθ1,…,Δym,Δem,Δxm,Δθm}

(11)

从C得出模型的输出变化量Δy，不可测输入变化量Δe,状态变化Δx和参数变化量Δθ，这些变化反映了系统的故障信息，将这些变化量(即特征信息)经过特定的算法进行提取，则可得出故障的征兆信息。

2 特征提取方法

为了准确有效地掌握发动机的运行状态，必须首先取得准确的诊断信息，从理论上说，任何运行中的机械都会有振动，机械的运行需要能量，能量的转化过程中就会有力发生，从而直接或间接地激起机械的某些部分振动。只有机械的运动是稳定的，或者其运行变化仅在一定范围之内，那么机械的振动也将是稳定的，而且当机械处于良好状态时，其振动频谱具有某些显著特征。当机械发生故障时运行状态会有重要的变化，其振动量和振动频谱也会发生明显的变化。因此，测量和分析振动信号的时域和频域变化是机械故障诊断的基础。时域分析是研究信号的形态随时间变化的规律，抽取必要的特征量(如幅值、周期、局部的上升时间与下降时间等)作为对信号判断与识别的依据；频域分析则是研究信号的能量或功率随时间变化的规律，从而为信号的进一步处理提供依据和手段。

2.1 振幅的特征提取

在对振动信号时域进行参数选择时，需要对振动信号时域数据作进一步处理后才能够作为故障判断的物理量，这是因为振动测试中得到的数据在大多数情况下不是真实的振动信号，或者说与真实的振动信号之间存在一定的差别，所以未经分析处理、修正，直接采用测试得到的振动信号作为结果往往会产生误差，有时甚至会得到错误的结论。在对振动信号进行时域处理时，需要用到的一个物理量是有效值，其数学定义如下:

(12)

式中：T为某一时间段；x2(t)为某一振动信号的数学描述。

从该式可以看出，有效值实际涉及的是一个振动时间变化的历程，它与振动信号能量的含量有直接的关系。在时域中另一个重要指标是振幅，它是发动机振动严重程度指标，可以用加速度来表示。通过对振幅的提取，可以很容易地判断发动机的振动状断以及发动机是否在稳定工作。对于特定型号的发动机，当发动机正常运行时都要求它的振幅稳定在某个限定区间内，振幅的任何变化都揭示了发动机的状态发生了改变。

2.2 功率谱特征提取

理论和实践都表明，在发动机发生故障前，高频部分信息中就已经出现故障的发展征兆，当低频信号出现异常时，则表明故障已经发生。因此，一个信号的高频成分对预示故障的发生有极其重要的作用，而低频部分则表明了故障发生时的故障模式。因此，对于振动信号的特征提取常常是以频域为基础进行的。

当系统发生故障时，其振动信号的频谱能量分布情况通常会有所改变，因此对振动信号进行频谱分析是当前常用的故障特征提取方法。在频谱分析中，最常用的就是功率谱分析法，功率谱分析的故障特征提取原理为：不同的部件所发出的响应能量谱的频率范围是不相同的。如果输出信号能量的空间分布与正常系统输出相比发生变化，就可以判别该频带所对应的部件应该处于异常的工作状态。通常某些频率成分明显被抑制，该频带内的信号能量减少，而有些成分被增强，该频带内的能量增加，对能量谱密度或功率谱密度进行分析计算，即可得出各种故障特征量。其具体的特征提取方法为：将振动信号的频率域划分为N个频带，分别计算各频带能量。当能量较大时，对应的各频带能量值比较大，为了计算方便，需要将所有能量值进行归一化，归一化公式为：

(13)

式中：ai为各频带的能量值；amax为ai中的最大值；amin为ai中的最小值。归一化后的值可以作为故障诊断所需的特征值。

2.3 频谱分析法

频谱分析是机械振动分析最常用的分析方法，每种特定型号的发动机在其工作时的频谱都具有一定特征，通过对这些特征的判断就可以有效地对发动机故障进行诊断，在该方法中谐频识别和边频识别是两种最重要的方法。

2.3.1 谐频识别

谐频特征提取法是根据谐频的间距判断基频，从频谱图中找出若干等间距的谱峰，通过对平均间距的确定从中找出高阶谐频上所隐藏的故障信息。应当注意幅值较高的谱峰并分析产生这些频率分量的原因，它们对振动的总量级贡献较大。值得一提的是振动频谱中有些振动分量虽然较大, 但不随时间而变化, 对发动机的正常运行也不会构成什么威胁。相反有一些幅值较小, 但增长很快的频率分量却往往预示着故障的产生和发展, 应该引起足够的重视。特别地, 当一些在原频谱图上并不存在或比较微弱的频率分量突然出现并急剧增大时, 极有可能在较短时间内破坏发动机的正常工作状态。因此，在频谱分析中不仅要注意各分量的绝对大小, 更应当注意各谱峰的发展变化趋势。一般来讲，当发动机出现故障时，在相应的频谱上会出现两个特征：一是振动幅值的上升，振动幅值上升主要是指数个测量频带振动总能量的上升，并包含其中某个单一频率(特别是主突频)的上升，同时要注意振动值是否已达到和超出有关理论标准参考值或是多次试车统计出来的参考值；另一个特征是谱型的变化，即在频谱上出现新的单一成分，或频谱上出现新的频带峰群，以及这些新的频率和频带峰群的幅值变化突然增大。根据以上振型变化，并结合以往若干次试车的历史数据综合分析对发动机的故障特征做出判断。

2.3.2 边频识别

边频是两个故障信号调制的结果，其调制信号可能来源于发动机不完全燃烧所造成的信号变化或由发动机本身局部零件部件缺陷所引起的信号突变，边频在频谱图中的反应是一个谱峰周围连续出现两个或两个以上的突频点，通过对边频间距的研究可以提取出发动机故障信息。

2.4 突频特征提取

振动信号的频域物理参数主要是频率，对于液体火箭发动机来说，振动频率与发动机转速有一定的倍数关系，发动机实际工作中涡轮泵振动主频频率与转速成倍数关系：

f=N/60

(14)

式中：N为涡轮转数；f为涡轮泵振动主频频率。

用频率来研究发动机的工作状态是一种简便、实用的特征提取方法。具体的特征提取方法为：每种型号的发动机都有固定的振动突频，并且突频与发动机的主涡轮转速有密切关系。通过对主涡轮转速的计算可以得到该型号发动机的主突频点，当发动机本身出现故障时，这些主突频点的位置和幅值会发生变化，通过在频谱图中找到有关的主突频点也就找到了故障的部位。一般情况下发动机的故障状态部位会激起各阶谐频振动的幅值，常以突频信号幅值增大作为故障状态的判据。图1所示为突频谱图。

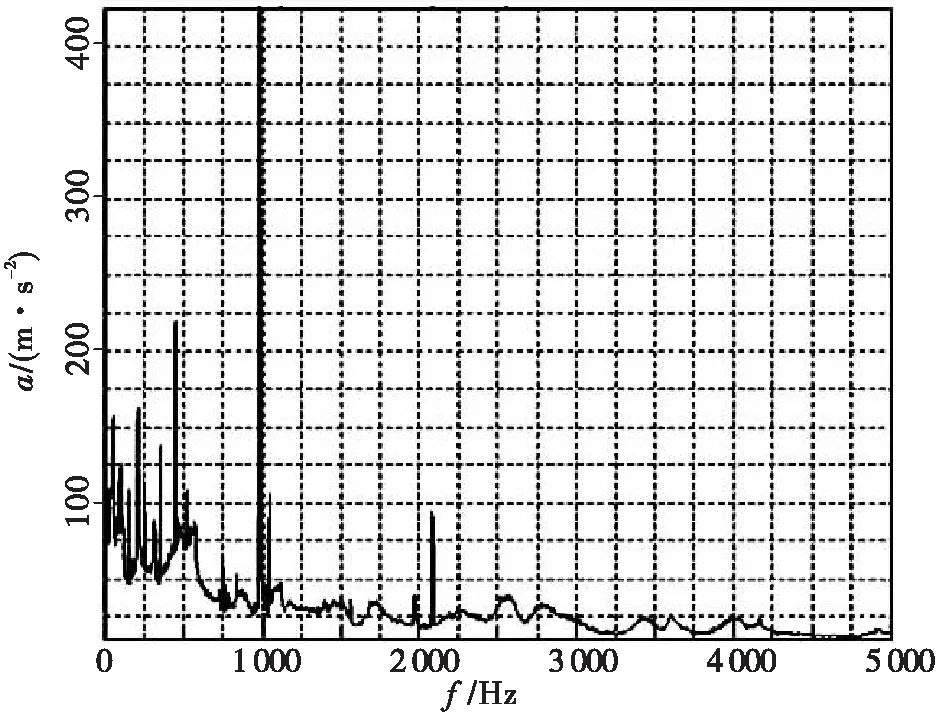
图1 基频谱图Fig.1 Fundamental spectrum

2.5 状态特征提取

振动状态特征数据是指通过FFT等相关信号处理手段，从振动的时域信号中提取的相关数据，包括振动信号的总振值、发动机主频以及各个倍频的幅值和残余量等。总振值是指振动时域信号曲线的最大值，各个倍频的幅值是通过FFT变换或其他信号处理算法将振动信号的时域信号转化为频域信号即频谱，然后在振动信号的频谱中提取感兴趣的特定频率点上的幅值。残余量是指振动信号的总极值减去已经提取的各个倍频上幅值后的残余部分，用来反映除去各个特征频率外其他频率上振动能量的大小。

2.6 小波特征提取法

信号分析的主要目的是寻找简单有效的信号变换方法，使信号所包含的重要特征能显示出来。上述谱分析方法在噪声的影响下振动信号频谱图起伏加剧，谱峰难以辨认。若信噪比较低，则振动信号的一些频谱特征将被噪声所淹没，严重影响谱估计的质量与正确性。谱分析的分辨力和噪声性能之间存在矛盾，在振动信号受到强噪声干扰的情况下，频谱分析难以兼顾分辨力性能和方差性能。由于经典谱分析法是建立在信号平稳性的假设上，而振动信号本质上是非平稳的，对于非平稳的振动信号的分析，使用谱分析法就会存在较大误差。

小波分析具有可以将信号按任意时频分辨率分解的特点[2]，将不同频段的信号分解到相应的频段中，然后可根据需要将所需频段内的信号重构，重构的信号与原来的信号长度一样，最后对重构的信号进行特征提取。具体的特征提取方法为：首先根据振动信号在各尺度(即各频带)上的小波谱具有不同的表现这一特点，对实际信号进行小波分解,选择小波并确定分解层次为N；然后对小波分解的高频和低频系数进行门限阈值量化处理；最后，根据小波分解的第N层低频和高频系数和经过量化后的1～N层系数进行小波重构，进而确定振动信号的特征信息。图2所示为振动信号小波分解图。

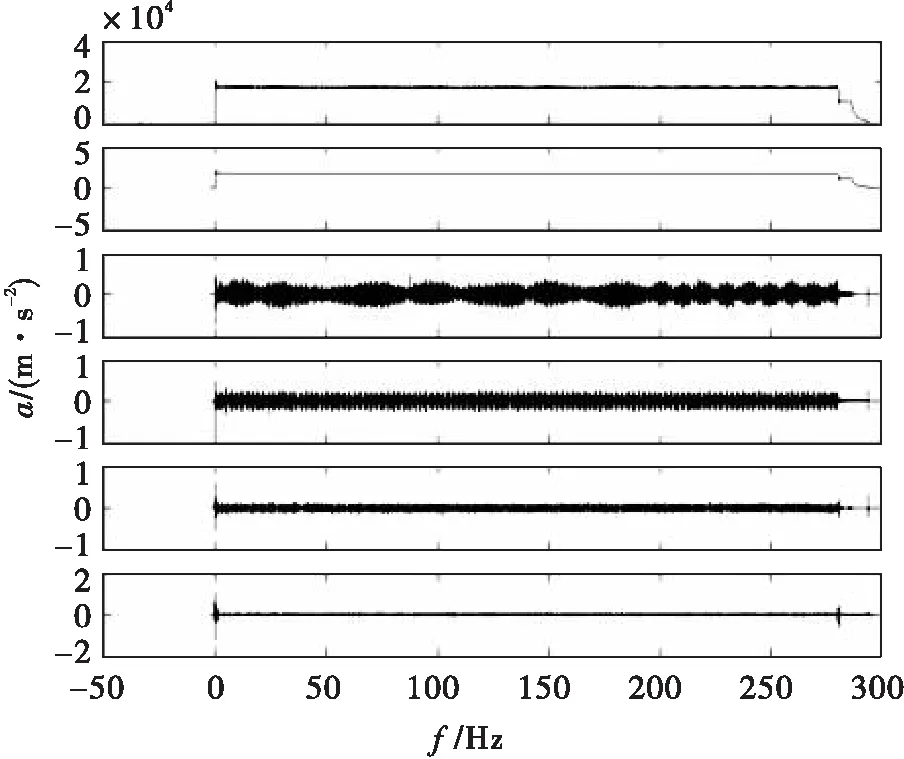
图2 振动信号小波分解图Fig.2 Wavelet decomposition of vibration signal

2.7 高阶谱特征提取

从统计学的角度看, 对正态分布的随机变量(矢量)用一阶和二阶统计量就可以完备地表示其统计特征。如对一个高斯分布的随机矢量, 知道了其数学期望和协方差矩阵,就可以知道它的联合概率密度函数。对一个高斯随机过程, 知道了均值和自相关函数(或自协方差函数) , 就可以知道它的概率结构, 即知道它的整个统计特征。但是对不服从高斯分布的随机变量(矢量) 或随机过程, 一阶和二阶统计量不能完备地表示其统计特征。或者说信息没有全部包含在一、二阶统计量中, 更高阶的统计量中也包含了大量有用的信息。高阶统计量信号处理方法, 就是从非高斯信号的高阶统计量中提取信号的有用信息, 特别是从一、二阶统计量中无法提取的信息的方法。高阶谱分析就是高阶统计量信号处理方法当中的一种重要方法，它是针对功率谱分析在实际应用中暴露出来的种种不足而提出的。高阶谱分析[3]从更高阶概率结构表征随机信号,弥补了2阶统计量的缺陷,同时,理论上高阶谱能完全抑制高斯噪声,具有很强的消噪能力,因而,用高阶谱分析振动信号更容易提取故障信息。

具体的特征提取过程为[4]：将获得的振动数据N分成K段，每段有M个数据，即N=KM，也可以重复分段，即相邻数据段有一半重叠，这样就有2N=KM；将每段数据中的均值变为零，然后对K段数据依次计算DFT系数；根据DFT系数，计算其三重相关系数；根据求得的三重相关系数进行统计平均，得到振动信号的双谱估计值。求取双谱估计值中的最大值作为信号的特征提取值。

3 液体火箭发动机故障诊断应用

由于发动机的振动信号是典型的随机信号,在发动机启动和关机阶段具有局部冲击信号的特点，同时,由于发动机会工作在不同的工况阶段，使其又具有平稳随机信号的特点。为此，在进行故障诊断算法选择和设计时，必须考虑到振动信号所具备的特点[5]。为了准确有效地对振动信号进行故障识别，必须要经过信号预处理、特征提取、状态识别和诊断决策四个主要阶段[6]。一个典型的液体火箭发动机故障诊断实现原理如图3所示[7]，其主要由振动传感器、信号调节器、数据采集系统、故障诊断模块、以太网数据传输系统、监控分析计算机、硬件扩展箱、信号控制、视频传输设备等组成。

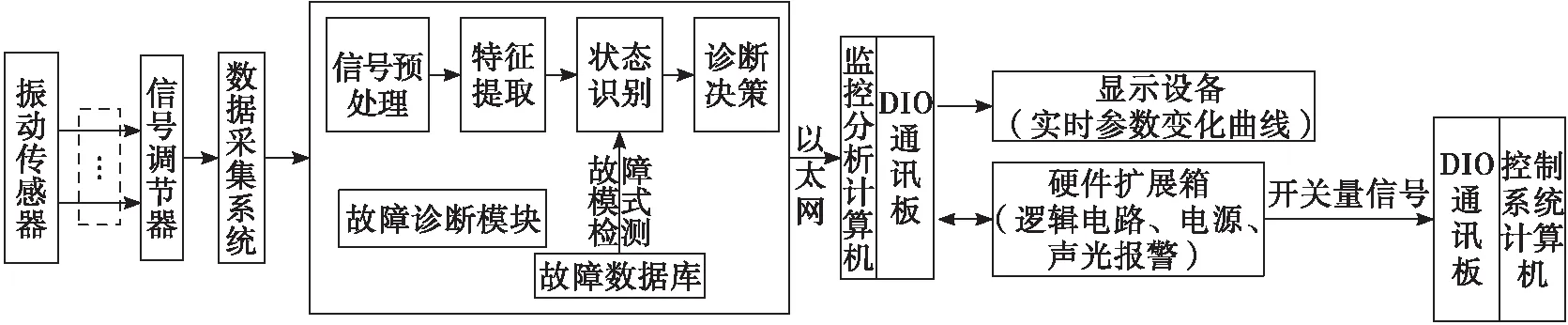
图3 发动机故障诊断方案原理图Fig.3 Schematic diagram of engine fault diagnosis scheme

在发动机试车过程中，测量振动传感器将被测信号转换成电信号，经信号调节器调节后送到数据采集装置，数据采集装置采集试车数据的同时向监控分析计算机通过以太网按不少于5 000 点/秒速率发送数据，参数是否超限由监控分析计算机判定。监控分析计算机中增加DIO板，将判定的结果通过DIO输出端口实时送到硬件扩展箱。硬件扩展箱完成参数超限逻辑判断、表决、声光报警及给控制台发送控制信号等任务。台上控制计算机对硬件扩展箱送过来的信号实时检测，最终完成试车紧急控制。

图3中整个系统的核心是故障诊断模块，该模块的核心就是信号的特征提取算法[8]。前文所介绍的振动特征提取算法的共同点均是从频域的角度进行信号的特征提取。但每种算法在应用场合上还有各自的应用范围和特点：振幅的特征提取优点在于振幅包络线设定方便、灵活简单，缺点在于包络阈值的确定不能准确实现，阈值设定宽了检测准确性差，设定窄了容易超量程引起误报警；功率谱特征提取法优点在于算法成熟，软件实现较容易，缺点在于其频率域N个频带的划分与发动机工作工况状态有关，不易进行实时准确划分；频谱分析法的优点在于仅针对频谱中的特征点和特征段，范围容易确定，缺点在于动态实时准确捕捉特征点和特征趋势的变化不易实现；基频特征提取法优点在于以转速基频变化为主要监测对象，实现容易，缺点在于该算法只能反映出与主涡轮有关的故障趋势，发动机其余部位故障反映不明显；状态特征提取法优点在于基于FFT算法，算法成熟，实现简单，缺点在于振动信号在算法实现过程中必须要满足FFT变换的定义条件，对于发动机启动段、关机段以及过渡段，该算法可信度不高；小波特征提取法优点在于该算法适用于发动机启动段、关机段以及过渡段实时分析[9]，缺点在于算法较复杂，软件实现实时性不易保证，且算法实现准确性与小波频率的选择有很大关系；高阶谱特征提取法优点在于弥补了功率谱分析的不足，缺点是算法复杂，由于算法实现过程中利用了FFT[10]，因此在算法实现过程中必须要满足FFT变换的定义条件[11]，对于发动机启动段、关机段以及过渡段，该算法可信度不高。

实际应用中上述特征提取算法可以同时使用，取长补短，如在发动机启动段、关机段以及过渡段利用小波特征提取法进行信号特征提取，在平稳段利用功率谱特征提取法、谐频、边频识别法、突频特征提取法、状态特征提取法以及高阶谱特征提取法进行信号特征提取[12]，只有这样才能正确地提取到振动信号中的故障信息。