大类资产配置在中国的应用——基于风险平价模型的实证研究

陆旻苏,陈宣宇,王昕杰

(渣打银行(中国)有限公司 财富管理中国投资策略部,上海 200120)

一、绪论

(一)研究背景

一直以来,马科维茨提出的均值—方差模型都是市场参与者进行资产配置时所采用的主流模型,然而该模型对于资产收益期望过于敏感,在实践中被证明不够稳健。因此,不论是学术领域还是从业领域都在积极寻求不依赖期望收益的资产配置模型,风险平价模型就是其中一个代表。

风险平价模型在2005年由钱恩平博士(Edward Qian)首次系统地提出,而从业内实践的角度来看,美国桥水基金(Bridgewater Associates)早在1996年就建立其第一只全天候基金,其背后的理论也是风险平价策略。该基金在成立后的2000-2002年美国市场大跌中表现亮眼,逐渐获得市场关注,随后大批资产管理公司,如贝莱德(BlackRock)、AQR等诸多明星机构都纷纷成立了自己的风险平价基金。

风险平价模型自2016年开始在国内开始流行。 在2017年9月8日,证监会公布首批公募FOF基金名单中,首批六支基金中有三支采用了风险平价策略，标志着国内投资者在投资观念上从“单纯追求绝对回报”到“在收益与风险中寻求平衡”的一个重大改变。 而风险平价模型收益适中而风险较低的特点,也将受到国内投资者的青睐。

(二)国内外文献综述

资产配置是指基于投资者的收益与风险目标,结合资产历史表现及市场宏观预期,按一定的模型来对组合内投资资产进行权重分配。而风险平价模型就是资产配置模型中的一种,从概念提出至今,学术界对此模型研究众多,本文在此对其中部分观点进行梳理。

1.国外文献

风险平价这一概念在2003年以前广受争议。William Sharpe在“Budgeting and Monitoring Pension Fund Risk”一文中指出投资风险贡献度并不适用,因为风险的衡量指标——标准差和VaR, 本身是不可相加的。 而与此同时,诸多学者都将风险研究聚焦投资风险的边际效应上,Chow和Kritzman[2]、 Grinold和Khan[3]及Litterman[4]等都对投资风险的边际效应有详细的叙述。

钱恩平首次提出风险平价模型[5],通过分析投资组合内资产标准差及VaR与资产贡献度之间的关系,并运用Cornish-Fisher展开模型,计算在收益非正态分布下的资产风险贡献度。为风险平价模型奠定了理论基础。

在此基础上,Maillard等人比较了等风险权重组合、等权重组合和最小方差组合,发现其发波动性位于等权重组合和最小方差组合之间,并验证了等风险权重组合在分散大类资产投资的前提下,采用风险预算方法来整体降低投资组合风险[6]。Lee发现, 在构建风险评价模型时, 可以通过按照资产对组合的β反比例进行配置,以达到平衡组合内各资产风险贡献度的目的[7]。

Chaves 等研究了风险平价模型组合、等权重组合、60∶40组合、最小方差模型组合及均值—方差模型组合在美国市场30年间的市场表现[8]。文章发现风险平价模型组合在夏普比率上虽然没有明显跑赢均分组合和60∶40组合,但明显跑赢最小方差模型组合及均值—方差模型组合。

Clifford、Andrea 和 Lasse研究发现投资者在相同情况下相较于高风险资产,会对低风险资产要求更高的风险调整回报,也因此驱动投资者在投资中使用杠杆[9]。风险平价模型平衡各个资产的风险贡献度以降低组合整体风险,并通过运用杠杆获取在较低风险的前提下获取更高回报。

Baltas对传统风险平价模型进行了升级,在结合了趋势追踪策略的前提下,以风险平价模型为基础,建立了多空组合模型[10]。该模型在1987-2013年的测试区间内,较传统风险平价模型拥有更好的市场表现。Roncalli和 Weisang提出以风险因子而非资产作为风险平衡对象,来解决在组合内资产相关性较高时,风险平价模型表现不佳的问题,并以APT模型为基础,提出了基于风险因子的平价模型[11]。

2.国内文献

国内学者风险平价研究起步较晚。 鲍兵运用2002到2014年间的中国股票市场作为样本,比较了多种资产配置模型的市场表现[12]。在不考虑交易成本及做空机制的前提下,风险平价模型取得较好的夏普比率,在资产分散程度上优于最小方差组合,总体而言,风险平价模型在中国市场会有较好的适用性。

高见和尹小兵以中债财富指数及上证指数为资产样本,比较了60∶40模型与风险平价模型在2007至2015年的表现,发现两种模型在收益近似的情况下,风险平价模型的波动性及最大回撤更小,而其夏普比率是60∶40组合的4.7倍[13]。付怡嘉通过考察2003至2015年内风险平价组合在国内市场的表现,认为风险平价组合适合运用于长线投资中,并在2008年金融危机间就60∶40组合体现出了更佳的抗跌性[14]。周亮和万磊测试了2013至2017年间风险平价组合与股债组合、股票组合及行业组合的市场表现,发现相较于最小方差组合与等权重组合,风险平价组合的夏普比率优于最小方差组合,并与等权重组合持平,综合看在国内市场有较强应用性[15]。

蔡文婕将资产类别由传统的国内上证综指及中债指数拓展至海外市场及商品市场,以避免国内股债两市的同质性。通过分层的方式在同质资产中选出最优,并在不同类型的资产层面上完成资产配置。测试结果表明分层策略较传统单一组合策略能提供更好的中长期收益[16]。徐美平和王力通过以资产波动率为基准构成的两种风险预算方法,在2010至2015年间与风险平价模型组合及传统切点组合进行比较。发现风险预算模型及风险平价模型在夏普比率方面都优于传统切点组合,并且风险预算模型克服了风险平价模型在分散方法上的单一性,可以根据不同风险偏好投资者的需求进行配比调整[17]。林逸帆在传统风险平价模型的基础上引入了收益率模拟及聚类方法,进一步提升了风险平价模型在市场波动情况下的表现[18]。

二、理论研究

(一)常规风险平价策略

风险平价模型是传统分散投资方法的延伸,在保持资产大类上分散的同时,通过调整资产配比使各资产对组合的风险贡献度相同,优化资产组合配置,避免组合暴露在单一资产的风险中。以一个简单的股票、债券按60%/40%的比例配置的投资组合为例,假定组合中股票的波动率为15%,债券的波动率为3%,股债之间的相关性为0.3,通过测算,股票对整个投资组合的风险贡献度为74%,而债券仅为26%。由此看出,即使投资组合在资产大类上进行了一定程度的分散,可是投资组合依旧严重暴露在股票资产的风险之中。而按照风险平价模型的核心思想,上述投资组合应大幅降低在股票上的配比,并同时加强债券权重,已达到两类资产风险贡献度相等,从而达到分散风险的目的。

为了方便讨论,我们在此假定投资投资组合内仅有两类资产,股票(Stock)和债券(Bond)。两类资产在投资组合内的权重分别为Wstock和Wbond,则有Wstock+Wbond=1。若以投资组合的波动性即标准差来衡量组合风险,则投资组合的总风险(标准差)为

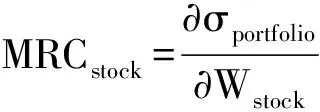
(1)

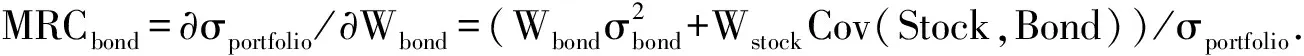
(2)

单个资产的风险贡献度(TRC)则为其组合权重与其风险边际影响的乘积,即

(3)

(4)

鉴于投资组合的总风险由组合内各个资产贡献而得,在本例中则有

TRportfolio=TRCstock+TRCbond.

(5)

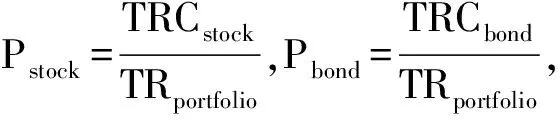
(6)

风险平价模型的核心就是构建一个投资组合内风险来源均衡的投资组合,那么参考上方推导,有Pstock=Pbond。基于此,根据公式(3)和(4)可以得出Wstock/Wbond=σbond/σstock。这说明在风险平价模型中,资产配置权重与其波动率成反比。拓展来说,如果投资组合内有多种资产,且各个资产之间相关系数为零,则Wi/Wj=σj/σi的关系依旧成立。当各资产之间的相关系数不为零时,应适当对正相关的资产减少配置权重,而对负相关资产增加配置权重。Lee认为,从市场实际情况来看,各大资产类别之间的相关性往往很不稳定,且估计误差常常大于波动性大的估计误差,在这种情况下,采取资产配置权重与其波动率成反比的关系进行估算所得出的结果经常比运用复杂模型所运算出的结果更加可靠[19]。

(二)加杠杆风险平价策略

风险平价模型在平衡组合风险来源的同时,也降低了组合内风险资产的投资比例,使得组合更倾向于投资债券类资产。从资产定价模型可以看出,当投资组合风险降低时,其预期回报也会同时降低。 因此,常规风险平价组合的收益可能对大多数投资者来讲不具备吸引力。但是如果假定投资者可以自由借贷,那么结果可能有所不同。

通过采样MSCI环球股票指数及Barclay环球政府债券指数在2008年1月1日到2018年1月1日的表现,我们构建了由上述两种证券构成的有效前沿,并将全债组合、全股组合、股债比6∶4组合,及常规风险平价组合进行标记(参见图1)。由纵轴无风险利率点出发经过风险平价组合点的射线上每一点均为不同借贷水平下的风险平价模型,该射线的斜率即为风险平价模型的夏普比率。我们观察图1可以看到,投资者可以通过加杠杆的方式从风险模型点沿射线向右上方无限延伸。因此,即使在有效前沿上风险平价模型点在6∶4组合的左下方,投资者也可以通过加杠杆将预期收益率提升至6∶4组合的相同水平,而组合波动率却明显降低。

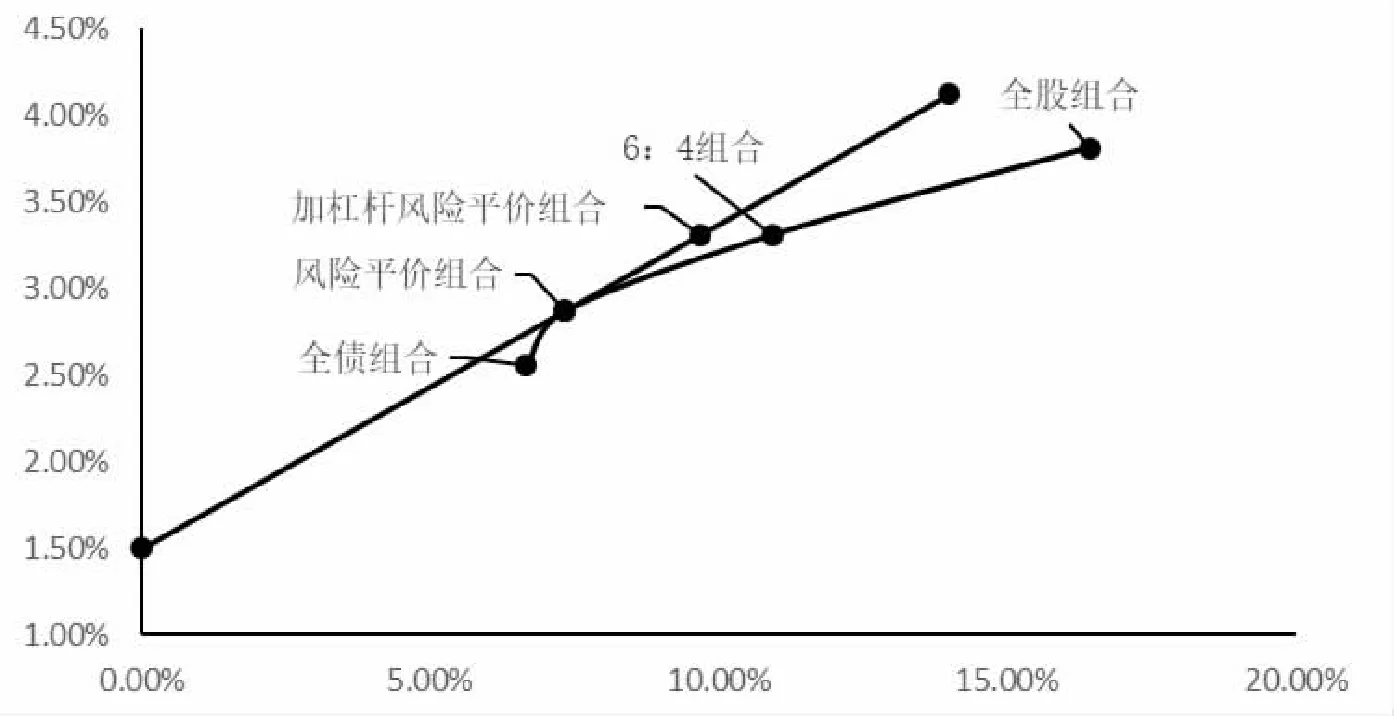
图1 由MSCI环球股票指数及Barclay环球政府债券指数构成的有效前沿

由上例可看出,风险平价模型较6∶4组合在夏普比率方面表现更加优秀,其通过增加杠杆而非增加风险资产配比的方式来提升组合预期收益,并降低组合风险。

三、风险平价模型实证研究

(一)数据选取及说明

本文选取的时间段为2004年一季度至2018年二季度,主要基于两方面考量:一是数据的可获得性;二是经历了两轮完整的经济中周期,不同资产间的轮动已经能够充分展现,有利于更加全貌地观测风险平价模型的检验效果。数据频率为季度,共计58个季度,年度组合权重频率太低,月度调整频率又太高且难以实际应用,从投资组合再平衡的合理性和战术性调整普遍使用频率的角度来看季度频率调整较为合适。所有数据均来自于Wind。

本文分别选取了上证综指、中债综合指数和CRB工业指数来拟合股票、债券和商品三种资产类别。上证综指为在上海交易所上市的全部公司股票加权平均指数,和深成指走势相似,能够比较具有代表性地反映中国股市走势和股票资产的回报情况。中债综合指数尽管不具备直接可投资性,但样本债券涵盖范围比较全面,能够有效反映债券资产类别的表现。商品资产类别上选取CRB工业指数,主要考虑到中国居民和机构的可投资性,目前中国大陆普遍仍然不会将黄金、农产品、化工原材料作为商品类别进行投资或者配置。

对于季度调整的交易成本设置为0.15%,为市场当前的ETF购买成本。对于无风险利率取一年期存款利率的加权平均值。对于加杠杆的融资成本取季度的隔夜质押式回购利率平均值,质押比例设置为前期债券持仓比例的70%。

(二)研究对象

目前国内主要资产配置方式仍然以股债混合为主,主要参考美国养老金60∶40的模式,风险评价策略的应用并不广泛,主要原因在于大类资产可选择范围不大,以及对风险的定价不够完善。本文试图通过在完整的两轮周期时间框架下建立股债两种资产类别的风险平价模型,和纯股、60∶40股债配置进行回报率、波动率、夏普比率、最大回撤等多个维度进行比较,发现在总体收益率水平相似的情况下,波动率和最大回撤显著下降,夏普比率明显提高。并且在股债两种资产的简单风险平价模型的基础上,通过单次质押式回购可增加杠杆水平50～70%,发现整体投资组合效率较不加杠杆的投资组合有所提高。此外,再次加入大宗商品用三种资产类别构建风险平价模型,发现尽管大宗商品单项资产回报率更高且风险更大,但组合总体收益率小幅下降,波动率明显下降,风险平价投资组合效率进一步提升。验证了国内通过风险平价进行资产配置仍具有一定的可取性。

(三)风险平价模型的权重设置

假设投资组合中只有两种大类资产,那么

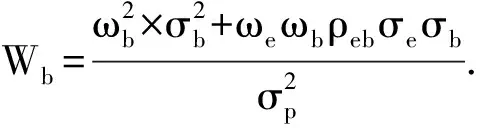
(7)

其中We和Wb分别代表了股票和债券的风险权重,

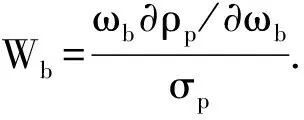
(8)

∂ρp/∂ωe和∂ρp/∂ωb分别代表了股票和债券权重变化对投资组合的边际变化,在风险平价的体系之下,所有资产的风险权重应当相当,并且风险权重之和等于1,推导出

We+Wb=1,且We=Wb.

(9)

因此在两种资产的风险平价模型下,

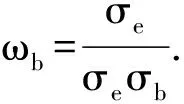
(10)

本文除了分析由两种资产组成的简单风险平价模型,还将相关性较低商品加入投资组合,来比较不同风险平价组合间的差异性。

在多种资产组成的风险平价投资组合中,应当考虑资产间的相关性,并相应调整权重。由于资产相关性波动较大,因此假设资产相关性为0,则每一类资产的风险权重应当相等。

We+Wb+Wc=1且

We=Wb=Wc.

(11)

得出具体权重为:

(12)

在增厚收益加杠杆的风险平价模型中,一次质押和完全质押根据前一期的债券持仓按70%比例进行质押加杠杆,之所以选择70%是因为对质押率的长期保守估计,两种模式下分别可增加杠杆率为:

(13)

(四)相关性和平稳性检验

对资产类别进行交叉的相关性检验,发现股票和债券呈现小幅的负相关性,债券和商品呈现较为明显的负相关,股票和商品呈现明显的正相关性(参见表1)。相关性检验得出的结果基本符合大类资产的运行规律,股票和商品具备一定的顺周期性,工业品价格和需求有较大关系,而股票价格在中国尽管不能充当经济增长的晴雨表,但从长期来看依然和企业盈利以及经济增长具有联系。由于债券和股票及商品均为负相关性,因此在投资组合当中将承受更多的权重和风险。

我们先对上证综指、中债综合指数和CRB工业指数进行了价格序列的平稳性检验,通过ADF单位根检验发现上证综指原序列在5%显著性水平下平稳。中债综合指数原序列不平稳,一阶差分后平稳。CRB工业指数原序列和一阶差分均不平稳,二阶差分才平稳,因此，如果使用价格序列,需要对三个指数都进行二阶处理。

进而对各项资产的回报率进行平稳性检验,上证综指、中债综合指数和CRB工业指数在任一显著性水平下,原序列都平稳,因此可使用回报率序列进行检验。

表1 资产间的相关性

表2 指数价格和回报率平稳性检验P值

(五)实证结论

1.不加杠杆的风险平价模型

如表3所示,股债60∶40的简单投资组合较纯股组合回报率和波动率都有所下降,但夏普比率有所上升,从纯股组合的0.15提高至60∶40组合的0.22,符合资产配置的基本原理,通过配置不同的资产类别能够提高投资组合的收益风险比。

观察股债组合的简单风险平价模型,累计回报为90.41%,年化复利为4.54%,从收益率角度基本和单纯股票配置基本一致。尽管累计回报率类似,但从2006年起股票组合的累计回报率均在风险平价累计回报上方且波动率较大,代表在该时间段之内开始投资股票的累积回报率小于风险平价组合。从风险角度观察,简单风险平价模型年化波动率仅为3.69%,远小于上证综指的26.2%,在最大回撤指标上也仅为5.52%,意味着风险平价在取得相似收益的情况下,所承担的风险远小于股票资产类别,其夏普比率为1.04,远高于股票指数的0.15。

对比同为资产配置的简单风险平价模型和传统股债60∶40组合可以得出类似的结果,两者在收益率方面较为接近,风险平价模型略微占优,但在波动率和最大回撤等指标上明显占优,夏普比率也明显高于60∶40组合。

2.一次质押和完全质押的风险平价模型

考虑到风险平价模型的年化收益率为4.54%,或许在中国无法满足部分投资者,本文试图通过增加杠杆的方式来增厚收益。由于二级市场机构投资者的股票质押并非主流,只计算债券头寸通过质押式回购按照一定质押比例进行加杠杆。

观察表3,可以发现在原有风险平价模型的基础上通过债券头寸加杠杆仍然能够保持累积收益率的平滑,收益率和波动率均较不加杠杆的风险平价模型有所上升,一次质押加杠杆和完全质押加杠杆的年化回报率分别为6.29%和8.39%,基本可以满足投资者对收益的需求,同时波动率分别为5.88%和10.11%,保持在较低的水平。并且夏普比率进一步提升,分别提升至1.26和1.27,意味着在适当提高收益率满足投资者的基础上,还提高了投资组合整体的收益风险比。

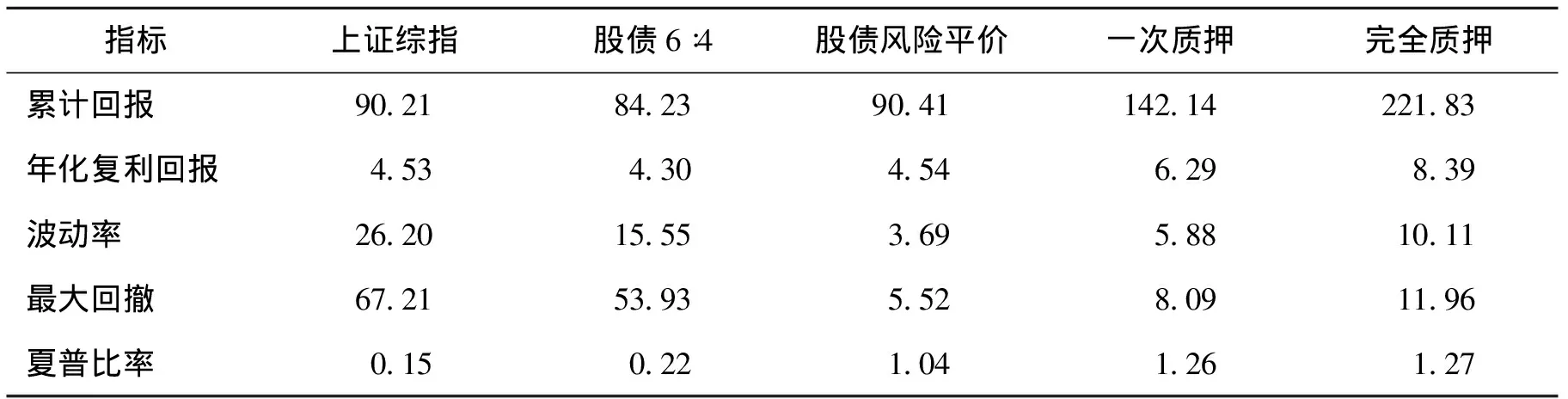
表3 股债风险平价和加杠杆风险平价与其他指数的各项比较(%)

3.加入大宗商品的风险平价模型

我们在股债风险平价模型的基础上加入商品资产类别,构建股票、债券、商品三种资产类别的风险平价模型,分别和股票、商品、股债60∶40组合和股债风险平价进行对比,详细结果参见表4。

与前文结论类似,加入商品后的风险平价模型和纯股票投资收益类似,但波动率更小,收益风险比更高。和纯商品相比较收益率略有差距,但同样在波动率和最大回撤方面具有明显优势,收益风险比更高。

尽管CRB工业指数回报率和波动率均相比股债风险平价模型更高,但股债商品的风险平价模型累积回报率反而小幅下降,同时组合的波动率明显下降,夏普比率从1.04提升至1.4,意味着投资组合的效率进一步提升。

如表5所示,对风险平价组合的收益率进行拆分,发现大部分收益率来自于债券部分,主要原因在于中国的资本市场对资产类别的风险定价还不是特别公允,尤其是股票指数的长期回报率和波动率并不匹配,导致在风险评价模型中债券比重偏高,在一定程度上使得模型的收益风险比相较于单项资产和股债60∶40有了显著的提高。

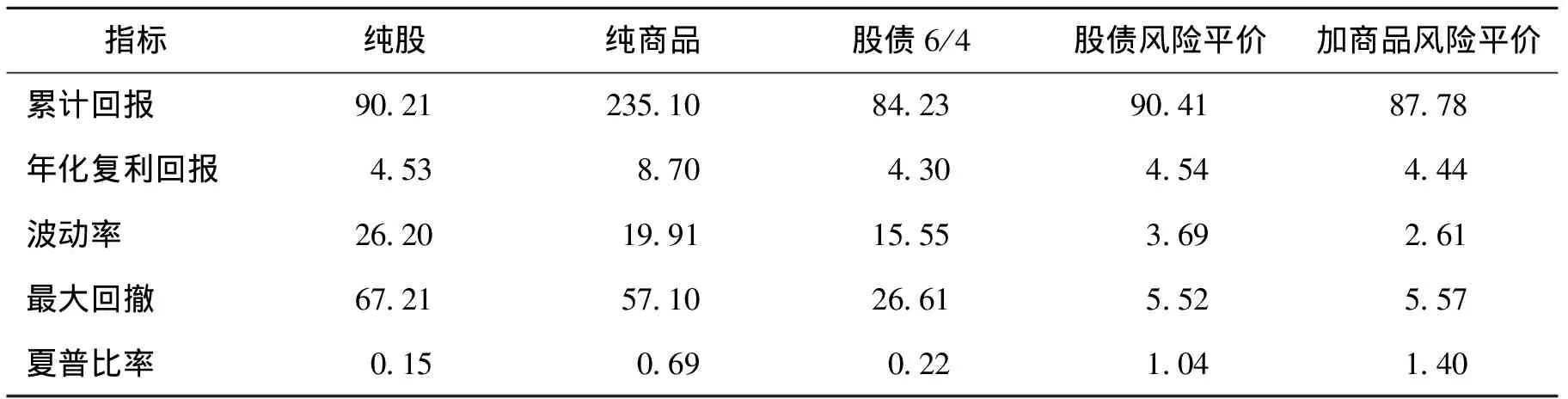
表4 股债风险平价和股债商品风险平价与其他指数的各项比较(%)

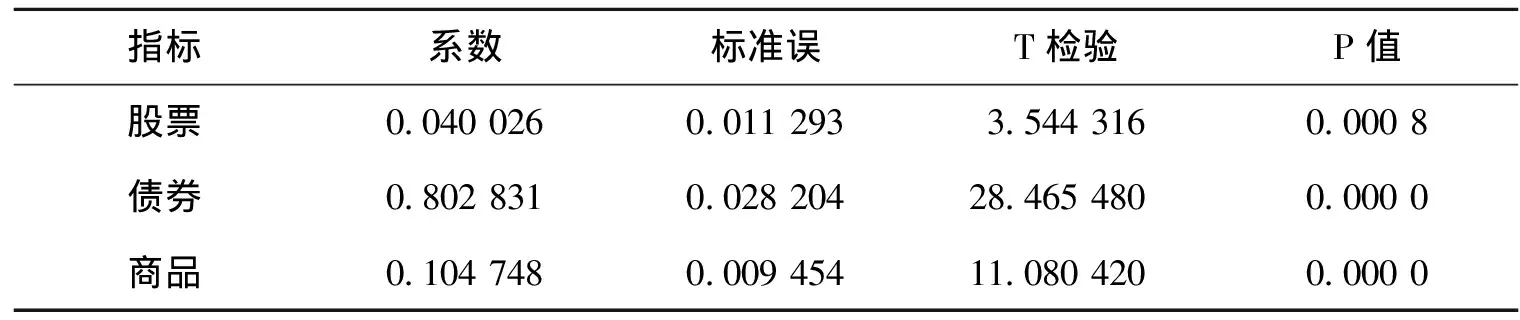
表5 风险平价模型收益率检验

四、结论和讨论

本文通过构建不同的风险平价模型,主要得出以下结论:(1)即使是最简单的股债60∶40组合,其在风险收益比优于各项单类资产,证明资产配置在中国可以具备一定的实际意义。(2)通过构建股债风险平价模型,在取得和纯股投资相似的回报率前提下,其波动率、最大回撤远小于纯股投资,并且在夏普比率上远远胜出。(3)为了适应中国投资者对收益率的需求,可适当通过质押式回购加杠杆增厚收益,使得年化收益率达到需求标准,并且一次质押加杠杆后和完全质押加杠杆后的风险平价模型的收益风险比较不加杠杆的风险平价模型进一步提升。(4)在股债风险平价模型中加入商品资产类别后,整体组合累积收益率没有太大变化的情况下,波动率进一步下降,并且收益风险比进而提升。不仅验证了资产配置的有效性,也验证了多资产类别的风险平价模型相较于简单资产配置组合具有更好的收益风险比。

当然,风险平价模型在中国的应用需要克服一些问题:(1)中债综合指数不具有可投资性,但其胜在样本涵盖范围更加全面,能反映债券资产类别的表现,在实际投资中应当使用其它可投资基准进行测算。(2)完全加杠杆未必符合机构投资者习惯,除了2015-2016年期间,其余时段均未出现债券投资者完全充分使用杠杆率的情况。(3)选取上证综指代表股票资产类别低估了股票资产类别的实际表现,市场上大多数公募长期能够跑赢指数。

尽管存在一些困难和实际应用中需要调整的地方,但风险平价模型作为资产配置的子类别,其有效性在中国市场能够得到验证。风险平价的本质是对风险进行定价而非单纯追求短期回报,金融市场本身面临较大的不确定性,资产价格的波动难以预测,资产配置对投资者而言变得愈发重要。随着资产管理行业将逐渐强调管理能力和定量能力,合理的风险平价设计能够使投资者取得一定收益率的情况下相对承担较小的风险,应当在市场中占据一席之地并引起管理人和投资者的重视。