生产性服务业集聚与城市生产率——差异化学习效应、选择效应与分类效应

一 引 言

对城镇化道路的选择,我国一直有大城市和中小城市之争。近年来随着大城市房价高涨、交通堵塞与污染日益严重,认为中国大城市规模过大、过于拥挤的看法越来越流行,然而以平均工资反映的平均劳动生产率,大城市远比中小城市高。黎日荣和周政(2017)[1]统计发现,制造业依然有向经济总量最大的十大城市集聚的倾向。李晓萍等(2015)[2]、周圣强和朱卫平(2013)[3]的实证研究发现2003年之后经济集聚对城市全要素生产率表现为显著的拥挤效应。这表明并非所有企业集聚均能提高城市的生产率。拥挤的大城市为什么依然有更高的生产率？大城市的高生产率来自于哪些集聚效应？在微观层面,哪些制造业企业会选址大城市？生产性服务业与制造业在性质上存在巨大差异,它们集聚对企业生产率的影响机制不同,分析总体经济集聚难以认清大城市生产率优势的来源。尽管有较多文献分析了生产性服务业集聚对制造业生产率的影响,但这些文献暗含了同质性假设,认为企业从集聚中获得了同样的集聚效应,产业获得的集聚效应是代表性企业的加总。现实情况是,生产性服务业集聚的大城市同时有大量企业迁入和迁出,表明并非所有企业从集聚中获得同样的溢出效应。哪些企业会被吸引迁入集聚区,哪些企业又会被“挤出去”,异质性企业如何与城市层级匹配？生产性服务业集聚如何通过影响异质性企业的选址行为,优化城市的资源配置？这些问题在同质性假设下均无法得到答案。本文基于异质性企业理论,认为生产率不同的企业具有差异化的学习能力,在集聚中获得差异化的学习效应,进一步导致企业差异化的选址行为,形成选择效应和分类效应。选择效应和分类效应又进一步影响城市的生产率和产业结构。本文使用城市统计数据和中国工业企业数据,检验拥挤效应、学习效应、选择效应和分类效应的存在性及大小,为生产性服务业成为大城市生产率优势的来源提供微观解释。

本文以下的结构安排是:第二部分是文献综述与理论分析,第三部分是模型与理论假说,第四部分是生产性服务业集聚对城市生产率影响的初步分析,第五部分是生产性服务业集聚的学习效应与选择效应,第六部分是生产性服务业集聚的分类效应,第七部分是结论与政策含义。

二 文献综述与理论分析

(一)生产性服务业集聚与差异化学习效应

随着社会分工深化,生产性服务业逐渐从制造业中剥离出来,成为服务经济的重要组成部分。自20世纪70年代生产性服务业概念被明确提出之后,逐渐引起学者的关注。随着生产性服务业由初期的润滑剂作用演变到当前的经济效率提升的引擎,学者的研究视角也由对集聚现象的描述深入到分析集聚对地区经济效率和制造业生产率的影响上。已有研究较为一致地认为,生产性服务业集聚对制造业生产率存在显著的溢出效应(陈建军和陈菁菁，2011[4]；顾乃华，2011[5]；宣烨，2012[6]；李敬子等，2015[7]；余泳泽等，2016[8])。张浩然(2015)[9]发现生产性服务业集聚显著提高了城市的经济绩效。惠炜和韩先锋(2016)[10]发现生产性服务业集聚能显著提高非农劳动生产率。这些文献为理解生产性服务业集聚提升经济效率提供了理论基础。归纳已有的观点,生产性服务业集聚提升制造业生产率有两个重要的渠道:(1)通过专业化分工降低生产成本。生产性服务业承接制造业生产中的非核心环节,通过自身专业化的生产,有效降低了制造业的生产成本,提高生产率。(2)学习效应。生产性服务是知识密集型产品,企业使用这些中间品,内含的知识会逐渐被导入企业，通过学习和消化,转化为企业的创新能力,有利于深化企业的专业化生产,提高生产率。

需指出的是，这些文献的实证分析普遍使用城市或行业的中观数据,也就暗含同一区域的企业是同质的。同质性假设存在两方面不足:(1)难以解释现实中异质性企业差异化的集聚特征。北京、上海和深圳是集聚上市企业总部最多的三个城市,并且在上市企业总部迁移中,北京和上海也是最重要的迁入城市(潘峰华等，2013)[11]。代表高生产率的上市企业显著倾向选址在北京等生产性服务业集聚城市的同时,有大量资源效率低的企业向核心城市的周边地区转移。不同技能的劳动力把知识和技术转化为现实生产力的效率不一样,高技能劳动力有更强的学习能力,在与其他劳动力交流和学习中能获得更大的技术外溢,因此高技能劳动力从生产性服务业集聚中获得更大的收益(Bacolod et al., 2009[12]；Glaeser和Resseger，2010[13]；Combes et al., 2012[14])。Combes et al.(2012[14]，2011[15])等指出高技能劳动力在高生产率企业能够发挥更高的效率，于是高生产率企业会内生地由高技能劳动力组成。本文把异质性企业从集聚中获得的差异化技术外溢效应称为学习效应。集聚给企业带来技术外溢的同时,也会引起对土地、基础设施等资源的激烈竞争,带来拥挤效应(周圣强和朱卫平，2013)[3]。高生产率企业由于能从集聚中获得更大的学习效应,倾向选址在生产性服务业集聚的城市,形成选择效应。低生产率企业从集聚中获得的学习效应较小,在拥挤效应的作用下,净集聚效应往往是负的,以致倾向选择外围城市,形成分类效应[注]值得注意的是,目前不同文献对选择效应、分类效应的界定略有不同。Baldwin和Okubo(2006)[16]认为集聚区有更大的市场,会吸引高生产率企业从非集聚区转移到集聚区,把这种转移界定为选择效应,相应的把低生产率企业从集聚区转移到非集聚区界定为分类效应。Combes et al.(2012)[14]认为大城市竞争更激烈,低生产率企业会被迫退出大城市,把这种退出界定为选择效应。本文遵照Baldwin和Okubo(2006)[16]的界定,把高生产率企业选址于生产性服务业集聚区界定为选择效应,把低生产率企业退出集聚区界定为分类效应。。(2)同质性假设未考虑异质性企业差异化的选址行为对城市生产率的影响。由于集聚存在选择效应和分类效应,导致生产性服务业集聚的城市内生地存在更多高生产率企业,不考虑企业选址行为对城市生产率的影响,把外溢效应全部归于集聚效应,往往会高估集聚效应的作用。另一方面不考虑企业的选址行为,也难以理解生产性服务业发展是优化城市空间资源配置的内生动力。

(二)分类效应、选择效应与城市生产率

尽管有文献很早就发现企业在生产率、规模和贸易行为等方面存在极大的差异,但直到Melitz(2003)[17],企业的异质性才被引入到主流经济学的分析框架,研究企业生产率差异对出口行为的影响。Baldwin和Okubo(2006)[16]开创性地将Melitz的异质性企业假设引入到Martin(1995)[18]的自由资本模型中,为研究异质性企业区位选择提供了理论基础。他们指出,集聚区市场更大,当运输成本下降时,为了实现规模经济,高生产率企业会从非集聚区转移到集聚区,即选择效应；当非集聚区政府提供转移补贴时,由于竞争力较弱，低生产率企业会最先从集聚区转移到非集聚区,即分类效应。Baldwin和Okubo的异质性企业选址模型开创了新新经济地理学时代,后续较多文献分析了异质性企业选址对生产率的影响。Saito和Gopinath(2009)[19]比较了选择效应和集聚效应对智利食品行业企业生产率的影响,发现选择效应更为重要。Combes et al.(2012)[14]基于法国工业区的企业数据研究发现,企业全要素生产率与区域就业密度有显著正相关关系,但区域生产率差异主要来源于集聚效应,并没发现有显著的选择效应。我国学者基于对中国工业企业数据的实证分析,得出的结论不尽相同。余壮雄和杨扬(2014)[20]发现集聚效应是解释大城市生产率优势的基本原因,同样没发现有显著的选择效应；刘海洋等(2015)[21]发现集聚效应和选择效应均能显著解释集群区生产率优势的来源；李晓萍等(2015)[2]发现1999-2002年,经济集聚主要表现为集聚效应,2003-2007年,经济集聚主要表现为拥挤效应,同时发现低生产率企业倾向选址在中小城市,即存在显著的选择效应；陈强远等(2016)[22]发现城市生产率溢价是集聚效应、选择效应、分类效应和竞争效应共同作用的结果。学者基于我国企业数据得出的实证结论远未一致,显然需要更进一步的分析。

已有新新经济地理文献主要是基于总体经济集聚,考察集聚效应、选择效应和分类效应的存在性及其大小。在不同产业集聚下考察这三种效应,可以更深入分析集聚区生产率优势的来源,理解生产性服务业是推动城市产业结构升级的内生动力。另一方面已有文献普遍强调下游市场规模对异质性企业的选择机制,并没有考虑上游中间品集聚对企业选址的影响。事实上企业选址不仅考虑规模经济,还考虑投入成本。上游市场集聚无疑能为企业提供质优价廉和多样化的中间投入品,降低企业的投入成本。赵曜和柯善咨(2015)[23]基于中国工业企业数据分析了城市规模、微观企业的中间投入对企业生产率的影响,但并未严格区分制造业中间品和生产性服务中间品,也未区分中间品是来源于本地市场还是外地市场。随着以制造智能化为特征的新一轮产业革命的演进,知识在制造业生产中的作用越来越重要,作为知识载体的生产性服务业已成为制造业创新能力和产品差异化的重要来源。现实经济中一个典型的现象是,大型制造业企业的总部往往选址在中心城市,以接近生产性服务业集聚区,生产工厂会分布在全国,以接近下游市场。因此研究生产性服务业集聚对异质性企业选址行为的影响是对新新经济地理文献的一个有益补充。综合而言，本文基于历年《中国城市统计年鉴》的数据和中国工业企业数据,分析城市生产性服务业集聚对制造业企业生产率以及选址行为的影响,有两方面边际贡献:(1)基于异质性企业理论,使用微观企业数据,考虑选择效应和分类效应能更准确地理解生产性服务业集聚对城市生产率的影响,也是对现有基于同质性假设,使用区域和行业数据分析集聚效应文献的有益补充。(2)本文分析上游高质量中间品市场集聚对企业选址行为的影响,为理解异质性企业选址行为提供了不同的视角,是对普遍强调下游市场规模对企业选址行为影响的新新经济地理文献的有益补充。

三 模型与理论假说

假设生产性服务中间品的生产遵循垄断竞争模式,城市共有n个生产性服务厂商,每个厂商生产1个差异化产品,服务中间品在城市间不可贸易。厂商k生产x单位生产性服务的成本为:Cx(k)=wcxxk,其中w是城市的均衡工资率,cx为劳动投入量(下标x代表生产性服务产品,y代表制造业产品)。制造业对生产性服务的需求遵循CES函数形式,不变替代弹性为σx,σx>1。生产性服务的价格px为边际成本的加成:

(1)

市场均衡时,城市生产性服务业价格指数PX为:

(2)

由于σx>1,城市生产性服务厂商数量n越大,价格指数PX就越低。这是生产性服务业集聚的价格效应,即越集聚,厂商的数量就越多,企业投入生产性服务的平均成本就越低。

Duranton和puga(2005)[24]假设企业的边际成本由商务服务、专业化中间投入和劳动报酬构成,本文借鉴这一假设,制造业企业的边际成本由生产性服务中间投入和劳动报酬构成,制造业中间品看作控制变量,省略并不影响本文的结论。异质性企业对中间品的使用存在效率差异,高生产率企业能更有效发挥中间品的作用,尤其是知识和技术密集型的生产性服务,高生产率企业从中获得的学习效应更大。本文假定城市的建设用地是既定的,生产性服务业集聚会对制造业造成拥挤,降低企业的劳动生产率,用λ(n)≥1代表生产性服务业集聚引起的拥挤效应,其中λ′(n)>0,表示生产性服务厂商越多拥挤效应越大。制造业生产遵循垄断竞争模型,每个企业生产1种差异化产品,企业i的边际成本hy(i)设为:

(3)

ρi为企业i的内在生产率,其概率分布密度和累积分布函数分别是φ(ρ)和Φ(ρ),μi反映企业生产性服务中间品与劳动的投入比例,其中0<μi<1。式(3)中λ(n)代表集聚的拥挤效应,PX(n)代表集聚的价格效应。企业的差异化学习能力通过以下两个渠道影响企业生产率:一是内在生产率ρi越高,企业会越有效率地使用生产性服务,中间品的实际价格(PX/ρ)就会越低；二是生产性服务的实际价格(PX/ρ)越低,企业在要素配置时会更多使用生产性服务,即μi更大。这两方面共同降低企业的边际成本,提高企业生产率,本文把它们概括为学习效应。企业从集聚中获得的集聚效应是价格效应、学习效应和拥挤效应的总和。当集聚效应大于零时,生产性服务业集聚会提高企业生产率。

借鉴Combes et al.(2012)[14]的模型,本文将代表性消费者的效用函数设为准线性函数:

(4)

消费者只消费标准化产品(一般指农产品)和差异化制造业产品。其中q0、qi分别代表消费标准化产品和第i种差异化产品的数量,Ω为差异化制造业产品集合。参数α、γ、η均大于0,α越大,η越小表示消费者相对标准化产品更偏好消费制造业产品,γ越大表示制造业产品间的差异性越大。在预算约束下最大化消费者效用函数可以得到产品i的价格pi:

(5)

(6)

(7)

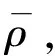
假说1:生产性服务业集聚对异质性企业的影响具有差异,集聚的学习效应和选择效应随企业生产率提高而增加。

企业能否从生产性服务业集聚中获得正的集聚效应,取决于价格效应、学习效应和拥挤效应的大小。由于学习效应与企业生产率正相关,所以有:

假说2:在生产性服务业集聚中,低生产率企业更有可能获得负的集聚效应；高生产率企业更有可能获得正的集聚效应。

假说3:由于低生产率企业更有可能获得负的集聚效应,集聚会提高低生产率企业退出市场的概率。

四 生产性服务业集聚对城市生产率影响的初步分析

(一)数据说明

微观数据来源于中国工业企业数据库,选取:13-37、39-42共29个二位码制造业行业数据。由于GB/T4754—2002版和GB/T4754—94版的 《国民经济行业分类》对生产性服务业的分类不完全相同,为确保统计口径的一致,本文只选取2003-2007年的数据。剔除了明显不合理的企业数据[注]具体整理方法参见文献黎日荣和周政(2017)[1]。,使用Brandt et al.(2012)[25]的方法把企业数据匹配成面板数据。城市统计数据来源于历年《中国城市统计年鉴》,剔除数据缺失较多的样本城市后保留218个地级及以上样本城市。通过城市代码把城市数据和企业数据匹配,得到地级市范围(包括辖区、辖市和辖县)的企业观测值共840802个。另外通过市辖区邮政编码识别市辖区和外围区企业[注]市辖区邮政编码经作者手工整理得到,邮政编码数据来源于全国邮政编码查询系统(www.yb21.cn)。,得到市辖区的企业观测值418423个,外围区(指市辖区之外的辖市和辖县)的企业观测值422379个。

企业全要素生产率是本文关注的被解释变量,OLS估计企业生产率会面临样本选择偏误和内生性问题,Levinsohn和Petrin(2003)[26]提出的半参数估计LP法能有效解决这两个问题,是目前估计生产率的主流方法。本文借鉴这一方法估计企业的生产率lntfplp(取自然对数的形式)。在估计中使用工业增加值衡量企业的产出,工业企业数据库没有报告2004年的工业增加值,本文使用刘小玄和李双杰(2008)[27]的方法推算2004年的企业工业增加值；分别使用企业员工数和固定资产净值作为劳动投入和资本投入的代理变量,使用中间品投入量作为代理变量控制生产率的不可观测冲击。为了剔除物价波动对生产率估计的影响,对以货币计价的投入产出变量均采用分行业投入产出价格指数进行平减,转化为以1998年为基年的真实值[注]为了增加样本容量更准确估计企业的生产率,本文使用工业企业数据库1998-2007年的样本数据估计企业的生产率。(Brandt et al.,2012)[25]。目前学术界对生产性服务业并没有统一的界定,本文借鉴王恕立和胡宗彪(2012)[28]的划分,将科学研究、技术服务和地质勘查业,交通运输、仓储和邮政业,房地产业,租赁和商务服务业,批发和零售业,信息传输、计算机服务和软件业,水利、环境和公共设施管理业,金融业界定为生产性服务业。目前文献普遍使用空间基尼系数、区位熵等指标度量产业的集聚程度,以分析其对行业和地区生产率的影响。本文关注集聚对企业生产率的溢出效应,认为生产性服务业就业密度越大,市场竞争越激烈,越有利于下游制造企业获取质优价廉的生产性服务中间品。就业密度更适合作为集聚指标以分析集聚对微观企业的影响,孙楚仁等(2014)[29]、Combes et al.(2012)[14]分析经济集聚对微观企业的影响时,也使用就业密度作为产业的集聚指标。本文统计发现2014年我国75%的生产性服务就业集中在地级市市辖区。余泳泽等(2016)[8]研究表明生产性服务业集聚对方圆200公里以内的制造业具有密集的溢出效应。这表明在200公里内生产性服务业具有较好的贸易性,市辖区的生产性服务业能有效覆盖周边辖市、辖县的制造业。为了更准确度量城市生产性服务业的集聚程度和竞争程度,本文以市辖区生产性服务就业密度Density1(单位为百人/平方公里)代理城市的生产性服务业集聚程度。为了考察溢出效应在不同集聚程度的城市是否存在差异,本文把218个城市按2003-2007年生产性服务业平均集聚程度从高到低分为4组,最高一组为高集聚城市(54个),次之为中高集聚城市(54个),再次是中集聚城市(55个),最低为低集聚城市(55个)。本文统计发现,低集聚城市、中集聚城市、中高集聚城市、高集聚城市2007年的平均GDP(亿元)分别为188、467、603、1220,这表明生产性服务业显著倾向于集聚在大城市。

(二)生产性服务业集聚的特征

表1是对不同城市的集聚密度和企业生产率分布的描述性统计。数据表明不管是全地区还是市辖区,生产性服务业在中高集聚城市和高集聚城市的样本明显比低集聚城市和中集聚城市多,这表明制造业和生产性服务业有显著的协同集聚特征。从市辖区数据看,高集聚城市的集聚密度明显比其他类型的城市高得多,高集聚城市的密度比中高城市的密度要高出238%,这表明生产性服务业有显著的集聚特征。从全地区看,随着生产性服务业集聚程度的提高,企业生产率均值总体有上升趋势,这一特征在外围区样本尤其明显,而在市辖区反而不明显，初步可以判断生产性服务业集聚总体上对城市制造业有正的溢出效应,但同时也给市辖区企业带来拥挤效应,以致市辖区企业的溢出效应并不显著。从企业的生产率分布看,市辖区p25(25分位点)的生产率均值为1.774,比外围区的1.775略低；但市辖区p90的生产率均值为2.087,比外围区的2.081明显高，初步可以判断市辖区企业生产率分布范围更广,但最高生产率的企业倾向集聚在市辖区。

表1 不同城市企业生产率及集聚密度的描述性统计

(三)基于核密度函数的初步分析

上文的数据描述性统计表明生产性服务业集聚与企业生产率总体上存在正相关关系,进一步通过企业生产率分布的核密度函数图探索正相关性的来源。Combes et al.(2012)[14]认为如果集聚的分类效应(把低生产率企业淘汰出集聚区, Combes et al.的原文把它界定为选择效应)存在,集聚区企业生产率分布会出现左截断的特征,如果集聚区的集聚效应存在,集聚区企业生产率分布会出现右移动的特征。本文对不同集聚程度城市的企业生产率分布图进行对比,从图1可以看出[注]为了更明显显示集聚效应和分类效应,作图所用的企业生产率数据为未取对数的全要素生产率。,左截断的特征并不明显,考虑到现实中制约企业退出的因素很多,总会有一些低生产率企业保留在市场,在分布图上出现左截断很困难。从市辖区样本看,高集聚城市的企业生产率分布图的左端较明显比中高集聚城市的低,即高集聚城市低生产率企业更少,这表明市辖区存在分类效应,但外围区分类效应并不明显。初步可以判断,生产性服务业在市辖区集聚会产生拥挤效应,拥挤效应会增加低生产率企业退出的概率。在外围区样本中,高集聚城市的企业生产率分布有显著的右移动特征,这表明集聚效应在外围区样本中显著存在,但市辖区这种特征并不显著。初步可以判断,在外围区价格效应和学习效应比拥挤效应更大,以致企业可以获得正的集聚效应；在市辖区价格效应和学习效应与拥挤效应大小相当,以致集聚效应并不明显。因此基于核密度函数图的初步判断是,生产性服务业集聚与企业生产率的正相关性,在外围区主要来源于集聚效应,在市辖区主要来源于分类效应。

五 生产性服务业集聚的学习效应与选择效应

(一)计量模型与变量设定

对企业生产率分布核密度函数图分析表明,市辖区样本中存在分类效应,外围区样本中存在明显的集聚效应。本部分进一步对数据回归,以判别集聚效应的来源以及分类效应和选择效应的存在。当前文献普遍使用OLS回归估计生产性服务业集聚的溢出效应,无法识别分类效应、拥挤效应、学习效应和选择效应的存在。事实上由于存在选择效应和分类效应,导致集聚区内生地存在更多高生产率企业,如果把溢出效应全部归结为集聚效应,往往会产生向上偏误。另一方面OLS回归也无法识别集聚对异质性企业的差异化影响。鉴于此,本文采用分位数回归,对全部企业样本每隔10个分位点回归一次,使用自助法获得稳健性标准误[注]作为对照本文也报告了全样本的OLS回归结果。。以往文献普遍认为企业的资产负债率、规模、资本密集属性以及所在行业均会影响企业的全要素生产率；城市的市场规模、产业结构、制造业密集度、人口密度、平均工资以及所在地区会影响企业的区位选择。本文在回归中控制这些变量,结合前文理论假说,基本回归方程设定如下:

Lntfplp=β0+β1Density1+Xβx+Yβy+νc+νr+νt+εjt

(8)

被解释变量为企业的全要素生产率Lntfplp,核心解释变量为城市生产性服务业集聚程度,用市辖区生产性服务业就业密度Density1表示。X为企业层面的控制变量,包括企业的资本密度K_intensity、企业的规模assets、企业的资产负债率fina_rest。Y为城市层面的控制变量,包括城市的人口密度den_popul、制造业的就业密度Density2(单位:百人每平方公里)、城市的实际平均工资wage；用第二、三产业产出占GDP的比重structure度量城市的产业结构；用实际GDP度量城市的市场规模。vc、vr、vt分别代表二位码行业、地区和年份效应[注]本文把大陆31个省市划分为三个区域,其中东部包括北京、辽宁、天津、河北、浙江、上海、山东、江苏、福建、海南和广东,中部包括山西、安徽、黑龙江、吉林、河南、江西、湖南和湖北,西部包括重庆、贵州、四川、云南、陕西、西藏、甘肃、新疆、青海、宁夏、内蒙古和广西。。εjt为随机干扰项。为了识别不同区位的溢出效应,分别对全地区样本和市辖区样本进行回归,核心解释变量均使用市辖区生产性服务业就业密度Density1,城市的其他控制变量,市辖区回归使用市辖区的数据,全地区回归使用全地区的数据[注]由于《中国城市统计年鉴》缺少对应辖市辖县的数据,本文并没有单独对外围区的样本回归。。

(二)回归结果与分析

(9)

Xi和βq均为向量,n为样本容量。分位数回归结果不易受极端值的影响,并且能够提供关于条件分布Lntfp|X更全面的信息。本部分通过考察企业生产率不同分位点上回归系数的差异来识别集聚经济的各种效应,分析的重点不是各分位点回归系数的绝对大小,而是各分位点系数的变化。

集聚经济的各种效应如图2所示。高生产率企业有更大的学习效应,从而倾向选址在集聚区,产生选择效应。由于两者的作用方向一致,均随生产率的提高而增加,两者的加总为一条向右上方倾斜的曲线。在本文的回归中并不能分别识别这两种效应,但可以识别它们的加总效应。表2的回归结果显示[注]限于篇幅,此处只报告核心变量的回归结果。,不管是市辖区还是全地区,各分位点Density1的系数均显著,且随着分位数增加,系数严格单调增加，表明生产性服务业集聚对各分位点的企业均有显著影响,溢出效应随企业生产率的提高而增加,证实了图2对总溢出效应的预测。由于拥挤效应和价格效应并不随生产率变化,分类效应随生产率增加而递减,所以溢出效应与企业生产率的正相关性,来源于学习效应和选择效应与企业生产率的正相关性。回归结果间接证实了学习效应和选择效应随企业生产率提高而增加,理论假说1被证实。由于差异化的选择效应是由差异化的学习效应延伸而来,回归结果也间接证实了学习效应随企业生产率提高而增加,即集聚效应(拥挤效应和价格效应并不随生产率变化)随企业生产率提高而增加。

为比较不同分位点间系数的差异,进行分位差回归IQR10-90,即90分位点和10分位点的回归系数之差,市辖区IQR10-90的系数为0.0225,全地区样本相应的系数为0.0164,两者在1%的水平上显著。如图2所示,假设X1和X2分别代表P10和P90,Y1、Y3、Y5分别代表X1处的溢出效应、学习效应和选择效应、分类效应；Y2、Y4、Y6分别代表X2处的溢出效应、学习效应和选择效应、分类效应。那么(Y2-Y1)代表X2和X1处的溢出效应之差,市辖区为0.0225,全地区为0.0164。由于X1处的分类效应Y5大于X2处的分类效应Y6,故有X2和X1处的学习效应和选择效应之差(Y4-Y3)大于(Y2-Y1),假设X1处(即P10处)的学习效应和选择效应为0(事实上低分位点企业的选择效应可以为0,但依然有正的学习效应),市辖区X2处(即P90处)的学习效应和选择效应为0.0225,全地区X2处的学习效应和选择效应为0.0164。即每平方公里增加100个生产性服务就业人口,学习效应和选择效应会使市辖区和全地区P90处的企业生产率至少分别提升2.25%和1.64%。这表明市辖区的学习效应和选择效应更强,高生产率企业更倾向选址在市辖区,该结论与前文描述性统计分析的判断一致。在P10-P90的区间内,企业生产率每提升10个分位点,市辖区和全地区企业的学习效应和选择效应分别增加0.28%(2.25%/8)和0.21%。在P90处,市辖区的学习效应和选择效应是总溢出效应的5.4倍(0.0225/0.0042),在P80处该倍数是10.6((QR80-QR10)/QR80=(0.0019+0.0183)/0.0019),其他分位点上学习效应和选择效应依然是正的,但溢出效应是负的,表明集聚中的分类效应和价格效应不足以抵消拥挤效应,集聚中正的溢出效应主要来源于学习效应和选择效应。这一结论在全地区样本同样成立。IQR50-90的回归系数,市辖区为0.0122,由于0.0122*2>0.0225,表明在市辖区,学习效应和选择效应随着生产率提高有加速增加的趋势。这一结论在全地区并不成立(全地区这一回归系数为0.0066,0.0066*2<0.0164)。这进一步表明高生产率企业倾向选址市辖区。

各分位点上,全地区Density1的系数均比市辖区大,表明生产性服务业给市辖区带来了更严重的拥挤效应。市辖区和全地区P10-P90九个分位点上回归系数的平均值分别为-0.0069和0.0053,表明市辖区的拥挤效应平均比全地区高1.22%(100%*(0.0053+0.0069)=1.22%),即每平方公里增加100个生产性服务就业人口,相比全地区,拥挤效应会使市辖区企业的生产率多下降1.22%。市辖区生产率在P80以前和全地区生产率在P30以前的企业,溢出效应均为负,生产率越低负效应就越大。由于低生产率企业的选择效应接近0,分类效应为正,即低分位点处的集聚效应小于溢出效应,溢出效应为负表明集聚效应也为负。高生产率企业的分类效应接近0,选择效应的发生往往以企业获得正的集聚效应为前提,所以在高分位点处溢出效应为正表明集聚效应也为正。即实证结果表明低生产率企业获得负的集聚效应,只有高生产率企业才获得正的集聚效应,理论假说2得到证实。制造业集聚对企业生产率普遍有显著的影响,与生产性服务业集聚不同,制造业集聚对市辖区企业有正的溢出效应,但全地区的溢出效应接近负数。可能原因是,生产性服务业集聚和制造业集聚都会产生拥挤效应,但两者的学习效应有差异。生产性服务作为一种中间投入品具有较高的可贸易性,带来学习效应的交流是有偿的,这有利于克服空间距离带来的障碍。制造业集聚的学习效应来源于交流的外部性,该种交流多属于员工的日常交往。所以制造业集聚的学习效应有赖于企业在较小空间的集聚,便于员工频繁交往。市辖区企业密集集聚,学习效应较大,扣除了拥挤效应依然有正的溢出；全地区企业比较分散,学习效应较小,不足以抵消拥挤效应的影响,表现为负的溢出。

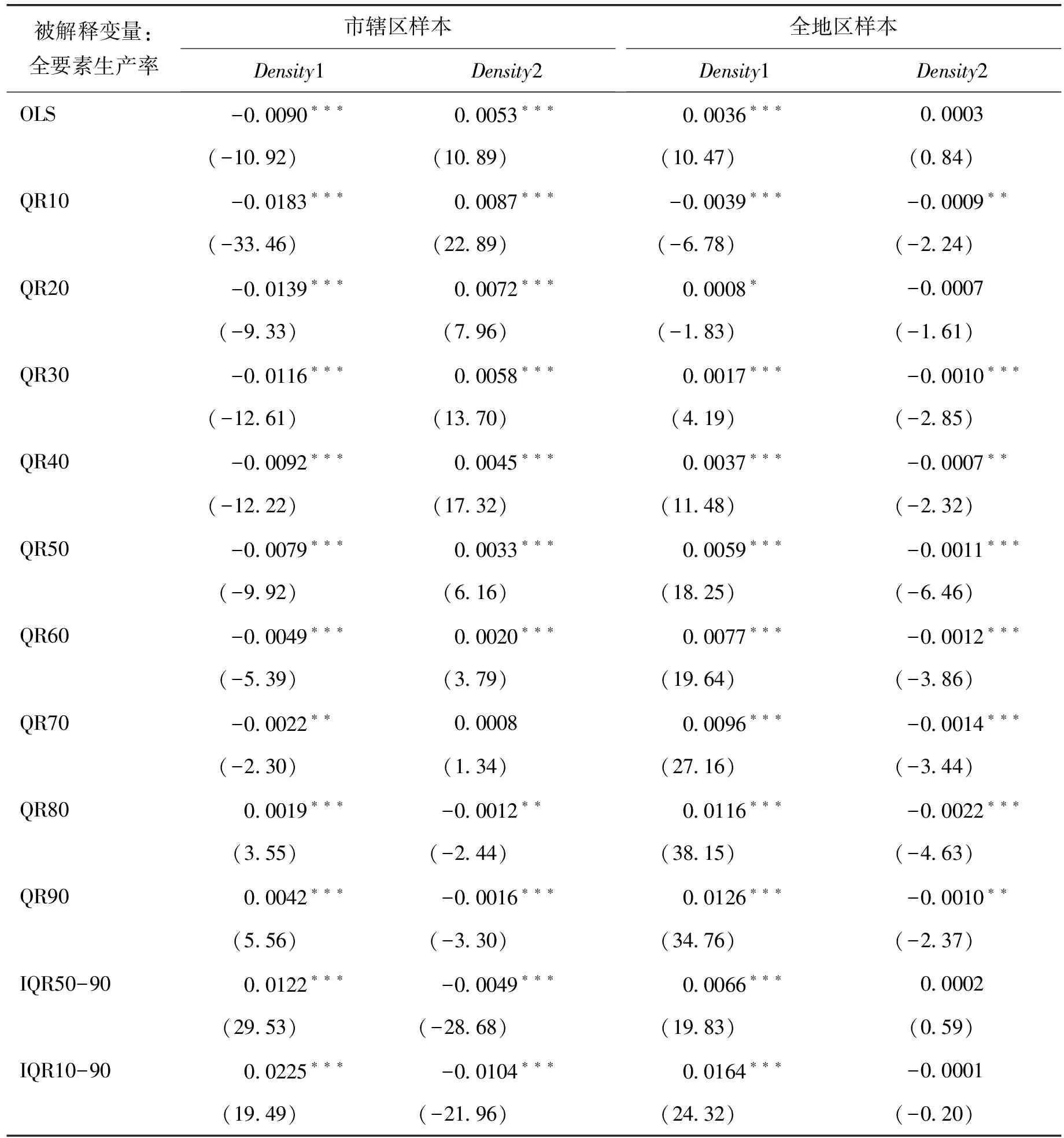
表2 分位数回归结果

注：括号内为稳健性t；*、**、***分别表示显著性水平为0.1、0.05、0.01。

六 生产性服务业集聚的分类效应

如第三部分所述,当企业的生产率低于临界生产率时,集聚的拥挤效应会使低生产率企业无利可图从而退出市场。结合本文的理论推导,第四部分的分位数回归也间接证实了低生产率企业的集聚效应为负。即随着集聚程度的提高,低生产率企业退出市场的概率会增加,本部分使用二值选择模型回归验证这个假说。Logit和Probit作为研究二值选择问题的经典模型,普遍被用于分析企业进入和退出问题。本文使用Logit模型分析企业的退出问题,模型设定如下:

(10)

被解释变量为企业退出市场的虚拟变量exitjt,exitjt可以取值1或0。当企业j第t+1年退出数据库,企业j第t年的exitjt变量取值1,否则exitjt取值0。由于2007年的数据用于判断企业在2006年是否退出,所以在回归中只使用了2003-2006年的数据。P(exitjt=1)表示企业j退出市场的概率。与第五部分的式(8)相比,本模型增加了两个变量,一是生产性服务就业密度与企业生产率的交叉项Density1×tfp,以识别集聚对不同生产率企业退出概率的影响。二是νjt,用以控制企业的个体异质性,其他解释变量和控制变量与式(8)相同。

表3回归结果中ρ的系数为企业不可观测异质性方差占总误差方差的比例,下方括号是它的P值。从结果可知4列的P值均为0,表明LR检验强烈拒绝ρ=0的原假设,该模型需要考虑企业的个体异质性,不宜使用混合模型回归[注]令nj为企业j存在期数的加总函数,T为面板数据的总期数,Logit固定效应模型的一个缺点是,在回归中会损失nj=0或nj=T的观测值,这意味着在回归中持续存在的企业观测值会被删除,本文数据是短面板数据,使用固定效应模型将损失大量观测值,以致回归结果不合理。本文使用随机效应处理企业的个体异质性。由于面板Probit没有固定效应模型,本文的Probit模型同样使用随机效应模型处理个体异质性。。值得注意的是,列(1)和列(3)中自变量的回归系数均已转化为几率比(odds ratio)的形式,系数大于1表明自变量与因变量有正相关关系,系数小于1表明自变量与因变量有负相关关系。先分析列(1)和列(3)的回归结果。Lntfplp的系数分别为0.1675和0.1889,且在1%的水平显著，表明生产率Lntfplp每提高1单位,全地区和市辖区企业退出的概率平均下降83.25%(0.1675-1=-0.8325)和81.11%,即生产率提高会显著降低企业退出的概率。全地区Density1的系数为0.9034,但不显著,市辖区为1.2691,在5%的水平显著,表明集聚对全地区企业退出概率的影响并不显著,对市辖区企业退出概率有显著的影响。每平方公里增加100个生产性服务就业人口,市辖区企业平均退出概率会增加26.91%(1.2691-1=0.2691)。进一步表明,集聚对市辖区企业有明显的拥挤效应,对全地区企业拥挤效应并不显著。全地区交叉项Density1×tfp的系数为0.9955,但不显著,市辖区为0.7845,在1%的水平显著,表明集聚主要“挤出”了市辖区低生产率企业,随着生产率提高,企业被 “挤出”的概率显著下降。以上结果表明,生产性服务业集聚对市辖区企业有显著的拥挤效应,增加了低生产率企业退出市场的概率,分类效应显著存在,理论假说3得到证实。理论上低生产率企业有两种策略应对集聚的拥挤效应,一是从集聚区转移到非集聚区,二是直接退出市场。本部分只考虑了企业直接退出市场的情况(即退出数据库),若考虑企业从集聚区转移到非集聚区,分类效应会更加明显。全地区Density2的系数为1.0034,市辖区为1.001,但均不显著。这表明制造业集聚对企业退出的概率没有显著影响。Logit模型假设累计分布函数服从逻辑分布,为了减少由于分布函数的设定导致回归结果的不稳健,本文同时使用Probit模型进行回归。值得注意的是Probit模型回归结果目前尚不能转化为几率比的形式,所有回归系数均不能与列(1)和列(3)的结果进行直接比较,但从回归系数的符号和显著性水平看,Logit和Probit模型的回归结果非常接近。这表明本部分得到的回归结果是稳健的。

表3 logit回归结果

注:括号内为稳健性z值；*、**、***分别表示显著性水平为0.1、0.05、0.01；ρ为企业不可观测异质性方差占总误差方差的比例,对应括号内数值是它的P值。

七 结论与政策含义

与现有大多聚焦于地区和行业层面的文献相比,本文进一步深化到企业层面,通过建立模型分析城市生产性服务业集聚对异质性企业生产率及选址行为的影响,指出生产性服务业集聚通过价格效应、学习效应和拥挤效应影响微观企业的生产率。高生产率企业拥有更强的学习能力,从集聚中获得更大的学习效应,倾向选址在集聚区,形成选择效应。低生产率企业的学习效应较小,在拥挤效应的作用下,生产率低于临界值的企业会退出集聚区,形成分类效应。最终生产性服务业集聚通过价格效应、拥挤效应、学习效应、选择效应和分类效应影响城市的生产率。本文使用中国工业企业数据库2003-2007年的数据对理论预测进行检验，结果表明:(1)生产性服务业集聚对异质性企业存在显著差异的影响,生产率越高集聚效应越大,低生产率企业的集聚效应普遍为负,市辖区只有生产率在80分位点以上的企业、全地区30分位点以上的企业才拥有正的集聚效应。(2)学习效应和选择效应随企业生产率提高而增加,溢出效应主要来源于学习效应和选择效应,集聚效应主要来源于学习效应,这表明高生产率企业倾向选址在集聚区。(3)拥挤效应显著存在,市辖区尤其严重,市辖区的拥挤效应平均比全地区高1.22%。(4)集聚显著增加了市辖区企业退出市场的概率,每平方公里增加100个生产性服务就业,企业退出概率增加26.91%,但随着企业生产率提高,被“挤出”的概率显著下降。这说明生产性服务业集聚主要提高了低生产率企业的退出概率,分类效应显著存在。(5)集聚导致城市生产率差异是集聚效应、选择效应和分类效应共同作用的结果,集聚的选择效应和分类效应能有效疏解大城市的落后产能,优化城市的空间资源配置。

中国经济经历了40年的高速增长后转入中高速增长的“新常态”，供需结构也发生了很大变化。2012年3月到2016年8月PPI连续出现54个月的负增长,这表明工业供给领域存在严重的产能过剩,由投入驱动的发展方式空间越来越小。提升全要素生产率将是未来经济增长的新动力,也是推进经济转型升级的措施和保障机制。发达国家全要素生产率对经济增长的贡献一般达到70%-80%,而我国改革开放以来平均水平只略高于30%(王一鸣，2017)[31],这既是巨大的差异也是巨大的潜力。自主技术创新和提升资源配置效率是提高全要素生产率的两个重要手段,然而自主技术创新难以在短时间内有大的突破,优化资源空间配置将是当前和未来较长时间全要素生产率的重要来源。

本文结论的三个政策含义:(1)弱化地方保护，淘汰落后产能。上文实证结果表明市辖区存在显著的拥挤效应。在市场决定资源配置的情况下,当城市出现过度集聚时,获得负集聚效应的低生产率企业会退出,直到拥挤效应和集聚效应达到平衡,经济集聚程度会回归到一个自然水平上。拥挤效应的存在表明企业退出可能受到非市场力量的干涉。地方政府出于就业、社会稳定和GDP考核的考虑,有动力对一些困难企业提供临时帮助；国有银行担心隐性坏账显性化,也有动力对一些“僵尸企业”提供信贷支持,以致“僵尸企业”长期存在于市场中。出于地区长期经济效率的考虑,地方政府要下定决心减少对低生产率企业的保护,让市场机制通过分类效应把“僵尸企业”淘汰,把土地、资金等要素配置给高效率企业,提高城市的全要素生产率。(2)抑制恶性竞争,促进企业自由迁移。在分税制下,地方政府倾向于保护地方经济,设置贸易壁垒曾是最主要的保护方式。但随着中国加入WTO,对外开放倒逼国内市场的一体化,地方政府的竞争逐渐转移到围绕招商引资而展开的“竞次式”补贴上。落后地区过度的补贴,往往招来的是发达地区的“僵尸企业”,并不利于落后地区的长期发展。企业作为理性人,选择最佳区位,使自身生产率得到最大的释放是其战略决策重点所在。随着中心城市或中心城区拥挤效应越来越明显,制造业企业有往周边迁移的动力,这样既可以接受中心城市生产性服务业的溢出效应,同时避免拥挤效应。落后地区应该先完善自身的基础设施,根据自身的产业特点以及离中心城市的距离制定合适的产业承接战略,而不是提供过度补贴展开恶性竞争。(3)发展大都市圈是释放全要素生产率的重要空间发展战略。本文的实证表明,全地区样本比市辖区样本获得更明显的集聚效应,表明制造业适度分散或与中心城区保持适度的距离更有利于获得集聚效应。大都市圈具有这种空间功能结构,中心城市专业发展生产性服务业,周边城市集聚制造业,既可以缓解中心城市的拥挤,同时接受中心城市的集聚效应。周边的制造业越多,给中心城市提供的市场就越大,中心城市的生产性服务厂商就越多,集聚效应就越大。