舱外航天服-航天员下肢系统动力学建模与分析

林如海，谢晓梅，李钰新，李学生，王振伟，徐利梅，王 枭

(电子科技大学航空航天学院，成都 611731)

1 引言

随着载人航天技术和深空探测技术的发展，未来航天员在月球、火星等地外星体表面开展资源勘探、基地建设和科学实验等出舱活动将是载人空间探测的重要组成部分。充压航天服为航天员出舱活动提供生命安全保障的同时，由于航天服充压后变硬及运动关节阻力矩的存在，将增加航天员的工作负荷、降低其工作效率[1-3]。因此，航天服活动性是航天服设计时需要考虑的重要因素之一。

迄今为止，航天员出舱活动大多属于太空作业，仅有美国在1961年到1972年期间成功进行了月面出舱活动。在执行太空出舱活动作业时，航天员下肢通常使用脚限制器来固定和稳定身体，操作任务主要通过上肢动作完成。随着航天服的不断改进，现有航天服上肢系统已具备了一定程度的活动性，但对航天服下肢系统活动性的关注度较少。未来的月球或火星探测任务，航天员进行舱外活动的时间更长、行进距离更远、作业任务更多更复杂，对舱外航天服上下肢系统的活动性提出了更高的要求[4]。如何提高航天服下肢系统的活动性，保证航天员着舱外航天服后具有行走移动能力将是未来航天服需要攻克的问题之一。

航天员在低重力环境下执行出舱作业任务时，舱外航天服对航天员作业能力的影响目前较多通过地面模拟实验进行研究，如抛物线飞行、中性浮力水池、气浮台等物理方法[5]。为了克服地面模拟技术难度大、实验成本高、时间周期长和操作风险高等问题，理论建模和数值仿真方法得到了部分学者的关注。早在1998年前后，Newman等就针对微重力下航天员运动的动力学问题开展了研究，在建立的多段人体模型的基础上，利用试验测试数据进行了运动学和动力学分析，填补理论航天员舱外活动定量分析的空白[6-7]。Rahn利用建立的舱外航天服动态模型，对多姿态舱外活动进行了模拟仿真[8]。王娟和庄达民采用拉格朗日方程法对失重人体建立了反向运动学和动力学模型，以模拟STS-63任务为例，确定了人体运动做功最少的关节活动范围[9]。杨峰等将人体模型简化为杆架模型，结合人体运动学和动力学，利用提出的力矩比优化方法对航天员出舱活动人体上肢运动进行了虚拟控制，估算了出舱活动作业时航天员上肢各关节的力矩[10]。李昊等就现有的航天员舱外太空作业动力学建模与仿真方法进行了探讨，建立了一套支持航天员舱外太空作业动力学仿真的软件平台，但未对着服航天员开展星表探测出舱活动进行模拟[11]。

为了较好适应未来星表环境下的探测任务需求，航天服下肢关节系统对航天员出舱作业能力的影响将为设计与评价舱外航天服性能提供依据。本文依据人体生理结构，建立航天服-航天员下肢系统简化物理模型，进行动力学分析；以步态行走、上下楼梯等典型下肢运动为对象，参考美国舱外活动单元(Extravehicular Mobile Unit，EMU)公开数据，对航天服质量、惯性和关节阻力矩对航天员下肢关节运动的作用影响进行数值仿真分析。

2 航天服-航天员下肢系统运动学分析

2.1 物理模型的建立

航天员在执行星表探测作业任务时，直立行走、弯腰拾物、屈膝等动作的实现都需要人体下肢各关节的参与配合。因此本文根据人体生理结构，考虑星表探测过程中肢体动作的多样性，配置航天服下肢系统髋关节、膝关节及踝关节的自由度分别为3、1、2。

根据我国现有航天员的身高体重参数，拟定航天员的身高为170 cm，体重为65 kg。人体下肢系统各体段的长度、质量和转动惯量的确定参考GB 10000-88(中国成年人人体尺寸)[11]和GB/T17245-2004(成年人人体惯性参数)[12]。

考虑到美国EMU航天服一直作为国际空间站的舱外航天服，而且公开数据较多，本文以该航天服为研究对象，确定对应的物理模型。EMU航天服下肢物理模型主要包括三个关键特性：质量、惯量和服装关节力矩[13]。其中，服装关节力矩具有极强的迟滞效应。航天服-航天员下肢物理模型中各项参数如表1所示。

2.2 运动学分析

2.2.1 正运动学分析

基于D-H参数法，在下肢各个关节处建立对应的下肢关节坐标系，如图1所示。其中，髋关节、膝关节和踝关节分别配置有3、1和2个自由度。

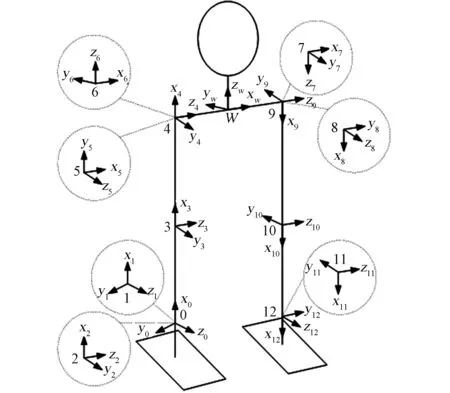
图1 下肢D-H模型Fig.1 D-H model of lower limbs

根据建立的坐标系及物理模型，确定下肢的D-H参数表，如表2所示。其中,l1是大腿的长度，l2是小腿的长度，l4是腰部的长度。θi是第i个关节自由度绕对应轴的旋转角度，取决于对应关节的运动范围。

表 2 下肢D-H参数

建立运动学方程时，可将两腿分别视为两个串联机构。摆动腿相对于支撑腿的运动可以视为腰部坐标系{W}相对于支撑腿运动和摆动腿相对于腰部坐标系{W}运动的叠加，这样可简化计算过程。

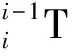
(1)

腰部坐标系{W}到基坐标系{0}的变换矩阵如式(2)所示：

(2)

坐标系{12}到坐标系{W}的变换矩阵如式(3)所示：

(3)

2.2.2 逆运动学分析

由图2(a)所示的人体下肢结构可知，当膝关节转角不为零时，无论腿部怎么运动，A、B、C三个点都构成一个三角形，且B点处的转角θ3的取值范围在[-π/2,0]之间。为此，采用解析几何法进行逆运动学分析[14]。

由正运动学分析可知，坐标系{6}到基坐标系{0}的变换矩阵如式(4)所示：

(4)

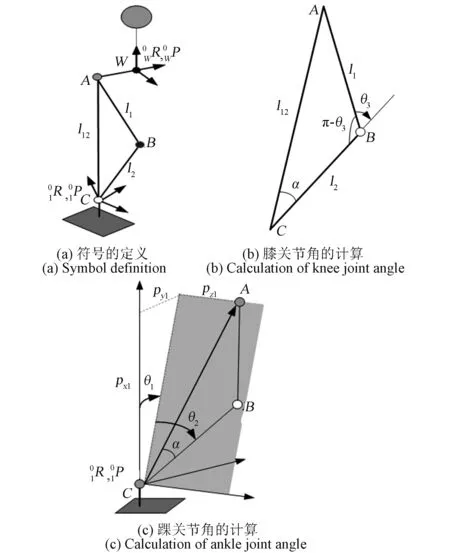
图2 逆运动学分析方法Fig.2 Inverse kinematics analysis method

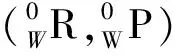
(5)

参考图2(b)可得，膝关节角度如式(6)：

(6)

在踝关节坐标系下，如图2(c)所示，根据l12可以求得踝关节的俯仰角和滚动角分别为式(7)、式(8)：

θ1=atan2(py1,px1)

(7)

(8)

式中，atan2(y,x)是用来求xy平面上的矢量(x,y)与x轴之间夹角的函数。sign(x)为符号函数，当x为正时取值为+1，x为负时取值为-1。

(9)

令公式(9)两边矩阵对应元素相等可求得式(10)～(13)：

θ234=atan2(r33,-(cosθ1r13+sinθ1r23))

(10)

θ4=θ234-θ2-θ3

(11)

θ5=atan2(sinθ5,cosθ5)

(12)

θ6=atan2(sinθ6,cosθ6)

(13)

3 航天服-航天员下肢系统动力学分析

星表出舱作业时，航天员着舱外航天服后需具有行走移动的能力。为了分析充压航天服对航天员直立行走过程中运动能力的影响，下面将对人服下肢系统的步态行走进行动力学建模与分析。

3.1 动力学建模

在前文完成的12个自由度的下肢系统正逆运动学分析的基础上，可以进行航天员-航天服系统的动力学分析，但求解十分繁琐和复杂。考虑到步态行走主要是矢状面内的运动，因此本文仅研究矢状面内的下肢运动。直立行走过程中，航天员的下肢运动姿态可划分为摆动相和支撑相。下面利用拉格朗日方程法分别对航天员的摆动相和支撑相进行动力学建模与分析。

3.1.1 摆动相动力学建模

下肢单腿摆动模型如图3所示，在此种运动模式下，髋关节与上躯干固定，模型简化为顶端固定的三连杆。

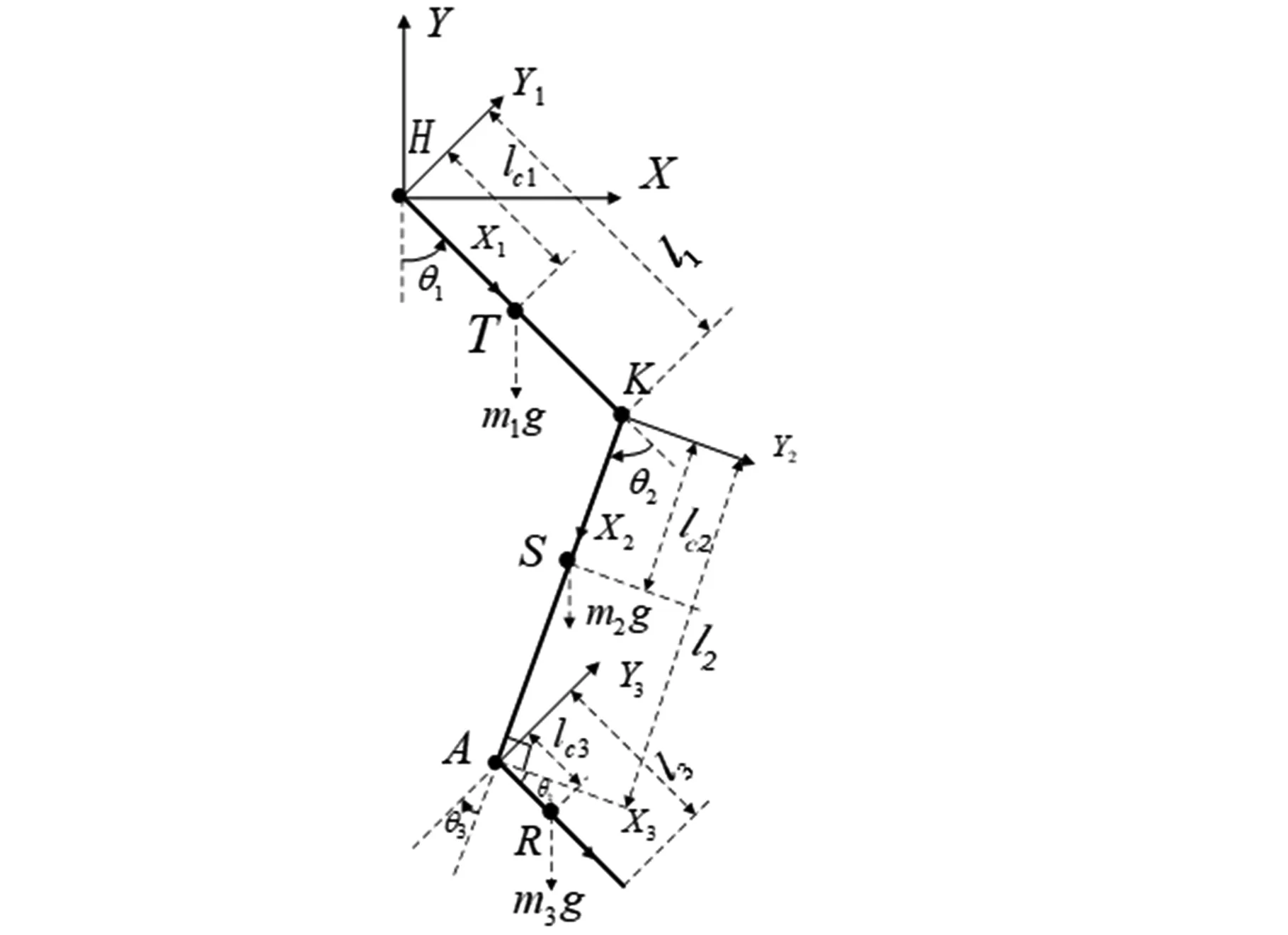
图3 摆动相模型Fig.3 Swing phase model

图3中：H、K和A分别表示髋关节、膝关节和踝关节；髋关节、膝关节和踝关节对应的角度分别为θ1、θ2和θ3，力矩分别是Mh、Mk和Ma，大腿和小腿及脚的质量分别为m1、m2和m3，长度分别为l1、l2和l3，质心分别位于T、S和R处，离关节中心的距离分别为lc1、lc2和lc3。

以XY为世界坐标系，则各杆件的质心(Xi,Yi)依次为式(14)～(16)：

(14)

(15)

(16)

则下肢单腿的动能如式(17)所示：

(17)

其中，Ii为各杆件绕其质心的转动惯量，φ1=θ1，φ2=θ1+θ2，φ3=θ1+θ2+θ3。

以X轴所在平面为零势能面，下肢单腿的势能如式(18)所示：

(18)

Lagrange函数L如式(19)所示：

L=K-P

(19)

Lagrange动力学方程如式(20)所示：

(20)

3.1.2 支撑相动力学建模

当人体下肢处于支撑相时，忽略脚底对踝关节位置的影响，同时忽略踝关节与地面接触，可以将模型简化为底端固定的三连杆模型，如图4所示。

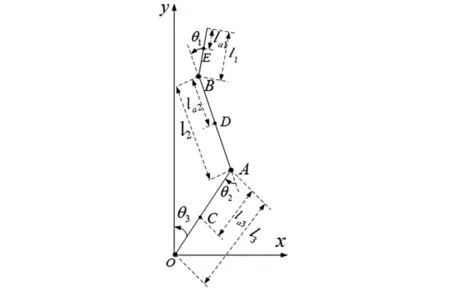
图4 支撑相模型Fig.4 Stance phase model

图4中：mi为各杆件质量，其中i=1,2,3；li为各杆件长度；lai为杆件质心距两杆交点的距离；θi为杆件间的夹角；B、A和O分别表示髋关节、膝关节和踝关节，髋关节、膝关节和踝关节对应的角度分别为θ1、θ2和θ3；躯干、大腿和小腿的质量分别为m1、m2和m3，长度分别为l1、l2和l3，质心分别位于E、D和C处，离关节中心的距离分别为la1、la2和la3。

以xy为世界坐标系，则各杆件的质心(xi,yi)依次如式(21)～(23)所示：

(21)

(22)

(23)

以x轴所在的平面为零势能面，Lagrange函数L如式(24)所示：

(24)

其中，φ1=θ1+θ2+θ3，φ2=θ2+θ3，φ3=θ3。

后续的动力学计算过程与摆动相类似，不再赘述。特别地，如图4所示的支撑相有两种情况：单腿支撑和双腿支撑。双腿支撑时，可将下肢模型分为左腿支撑和右腿支撑模型，两种模型的动力学模型计算方法类似，只是躯干处的质量和质心位置有所不同。

3.1.3 动力学分析

月球上的低重力环境使得航天员在月球上的步态行走与地球上存在一定的差异，但由于航天员在月表行走的下肢各关节步态数据难以获取，本文拟使用临床步态分析数据CGA(Clinical Gait Analysis)[15]作为航天员步态行走运动曲线，进行后续的动力学分析。定义一个步态周期为1 s，下肢各关节角度的定义如图5所示。以逆时针方向为正方向，髋关节角为垂直轴到大腿中心线的角度，即θhip；膝关节角为大腿中心线到小腿中心线的角度，即θknee；踝关节角为小腿中心线到脚底平面法线的角度，即θankle。各关节角度曲线如图6所示。

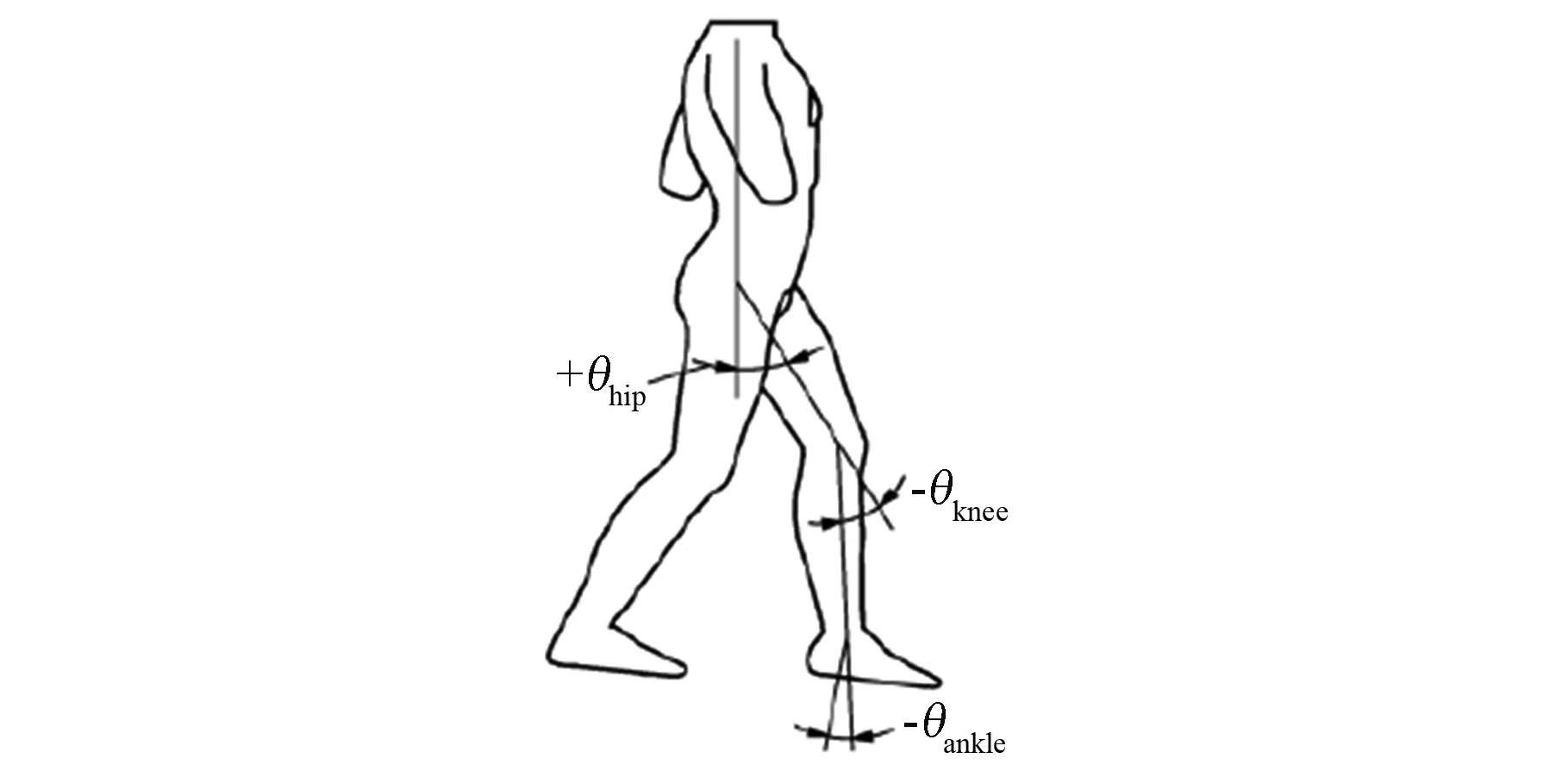
图5 人体步态数据定义Fig.5 Definition of huma gait data

图6 关节角度曲线Fig.6 Joint angle curves

将表1所列航天员肢体物理参数及CGA步态数据曲线分段(前60%为支撑相曲线，后40%为摆动相曲线)代入支撑相和摆动相动力学模型中，可得到航天员一个步态周期内髋关节、膝关节和踝关节关节力矩变化曲线，如图7所示。可以看到，髋关节所受力矩最大，在支撑相末期达到最大力矩，随后进入摆动相，关节力矩减小。膝关节的正负力矩极值近似，而踝关节的关节力矩波动最小。

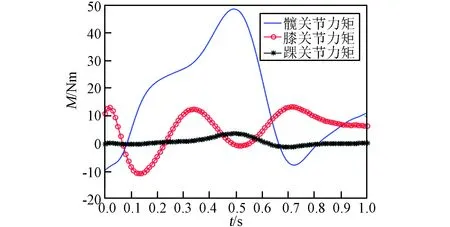
图7 关节力矩曲线Fig.7 Torque curve of joints

3.2 着服航天员下肢系统动力学分析

3.2.1 着服航天员直立行走关节力矩分析

航天服对航天员下肢系统的影响主要表现为质量、惯量以及服装阻力矩对关节力矩的影响。因此着服航天员下肢系统动力学模型由着服未充压航天员下肢系统动力学模型和充压关节阻力矩模型组成。 着服未充压航天员下肢系统动力学模型可采用上节相同的方法建立，此处不再赘述。需要说明的是，拉格朗日函数L的推导过程中质量和惯量均为人服系统的总质量和总惯量。充压EMU航天服下肢关节角度与力矩关系曲线采用文献[16]提供的角度力矩迟滞曲线。图8给出了一个步态周期内，关节阻力矩随时间的变化曲线。

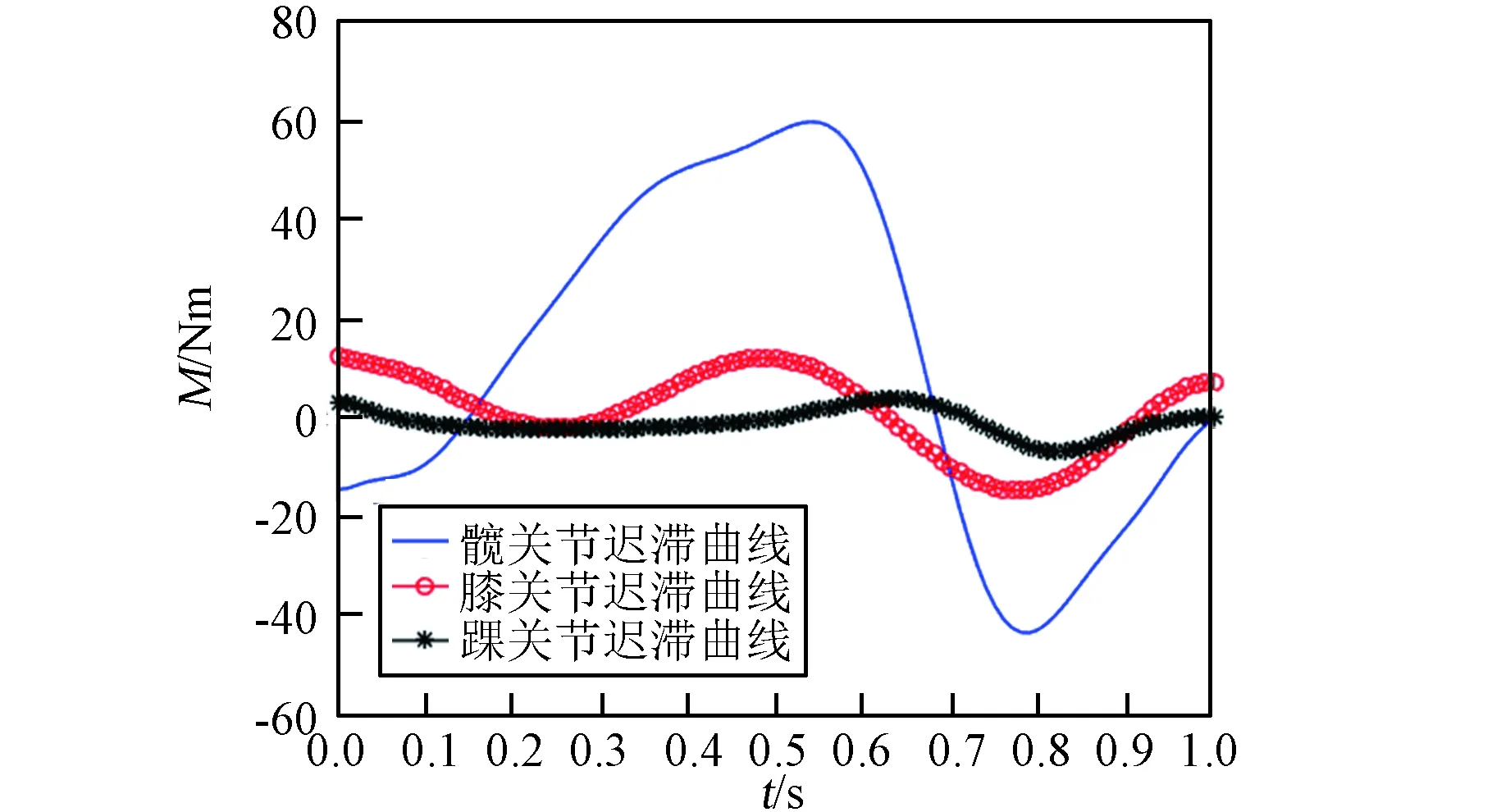
图8 关节迟滞曲线Fig.8 Hysteresis curve of joints

图9～图11汇总了航天员未着服、着服未充压以及着服充压三种情况下，完成一个步态周期动作时航天员下肢各关节的关节力矩。

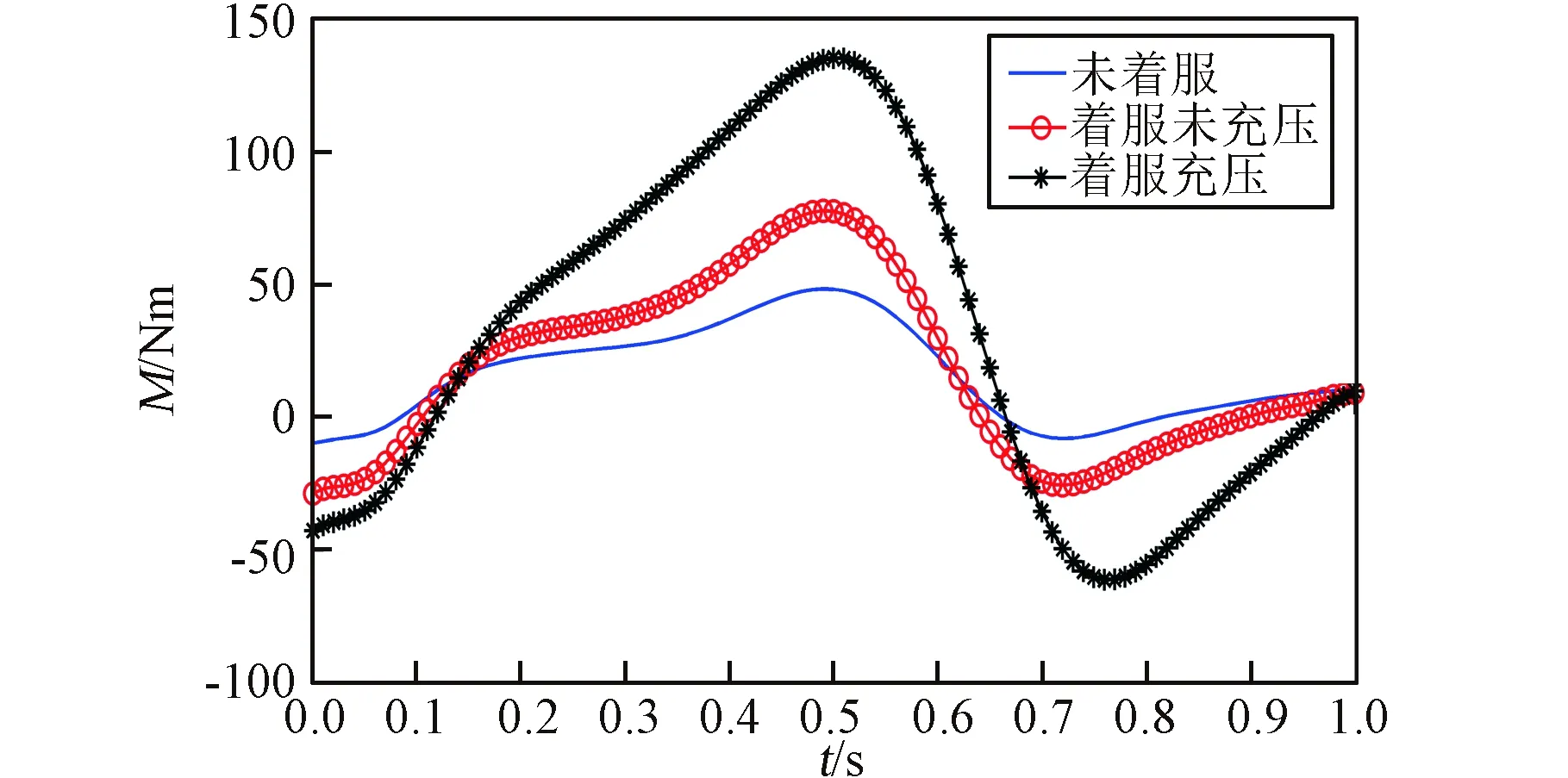
图9 不同情况下髋关节力矩对比Fig.9 Comparison of hip torque under different conditions

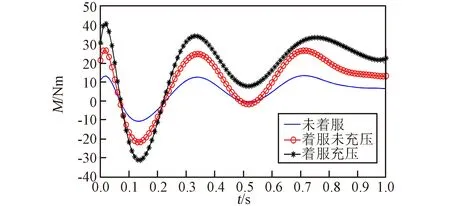
图10 不同情况下膝关节力矩对比Fig.10 Comparison of knee torque under different conditions

图11 不同情况下踝关节力矩对比Fig.11 Comparison of ankle torque under different conditions

图9～图11所示曲线表明，当航天员在未着服、着服未充压和着服充压状态下完成相同的直立行走运动，航天服质量、转动惯量和服装关节阻力矩导致人体下肢各关节的关节力矩明显增加。对比各关节着服充压与未着服的力矩变化，髋关节力矩增加幅度为[-40，90]N·m，膝关节力矩增加幅度为[-15，25] N·m，踝关节力矩增加幅度为[-4，8] N·m。

航天员在一个步态周期内，当下肢各关节按照CGA时间角度曲线运动时，各个关节所做的功可以通过表达式(25)计算：

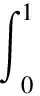
(25)

式中，M表示关节力矩，ω表示关节角速度。通过计算，航天员在未着服和着服状态下的下肢各关节在一个步态周期内的总功列入表3。

表 3 未着服与着服时关节总功值

由表3可以看出，在一个步态周期内，着服航天员髋关节、膝关节和踝关节所做的功比未着服时分别增加了205%、134%和95%。在这种情况下，航天服会增加航天员的能量消耗，肌肉的疲劳会比预期更快。

3.2.2 不同路况下着服航天员关节力矩分析

航天员在月面开展出舱作业时，因月面崎岖不平或探测任务需求，将在上下坡、上下楼梯或平地等路况下行走。有研究表明，人体步态在不同路面状况下表现出不同的特征，如不同路况下支撑期和摆动期在整个步态周期内所占的比例不同，髋、膝和踝关节所需力矩不同，其中支撑期差别最为明显[17]。文献[18]和[19]分析了行走、上下楼梯过程中下肢关节角度的变化。

图12 正常步态力矩对比Fig.12 Comparison of torque in normal gait

依据前文建立的动力学模型，参考文献[19]在正常行走、上下台阶给出的下肢关节在矢状面内的运动角度时间曲线，图12、图13和图14分别给出了未着服和着服未充压状态下航天员正常行走、上下台阶时下肢关节角度和力矩变化曲线。由于上下楼梯关节角度变化较大，角度限值超过文献[16]所示的充压航天服关节迟滞曲线中的角度值，因此，本文仅分析了航天服质量和惯性对关节力矩的影响。

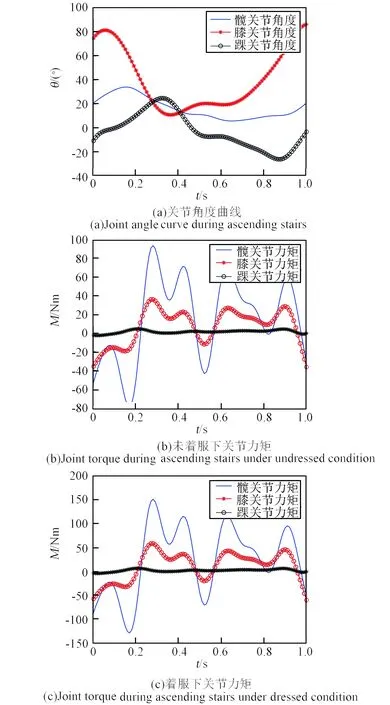
图14 下楼梯力矩对比Fig.14 Comparison of torque during descending stairs

从图12～14可以看出，上下楼梯过程中髋关节和膝关节的角度变化范围大于正常行走的角度变化，因此，在未着服和着服状态下，髋关节和膝关节处关节力矩极值均大于行走过程中相应极值。以上楼梯为例，未着服情况下，髋关节力矩变化范围为[-47.0, 129.9]N·m，而着服状态下，髋关节力矩变化范围为[-75.3, 204.3]N·m；膝关节力矩变化范围由未着服状态下的[-30.6, 50.2]N·m变为着服状态下的[-48.4, 82.4] N·m。可以看到，航天服质量和惯性的存在使得着服航天员需要消耗更多的能量来完成相应的动作，从而影响航天员的工作效率。

4 结论

1)正常步态行走过程中，舱外航天服的质量、惯性和关节阻力矩增加了航天员下肢关节的运动负荷，而且髋关节受到的影响最大。

2)不同的路况下行走时，髋关节、膝关节和踝关节的步态特征不同，舱外航天服对各个关节的影响不同。

因此，综合分析不同路况下航天服对着服航天员运动负荷的影响，合理确定航天服质量、航天服关节结构形式，降低航天服对航天员活动性和操作能力的影响是非常必要的。本文在进行航天服-航天员系统动力学建模时，认为人服的关节位置完全重合，将人体下肢各节段假设为刚体，而将航天服作为人体模型的附加质量和惯性进行考虑，步态分析数据也基于地面步态测量，未考虑低重力环境对步态引起的差异。这些方面都需要进一步探讨，后续可在OpenSim软件平台下，建立人体骨肌模型模拟人体的真实的生理结构，同时引入航天服属性，通过人服耦合的动力学分析，评估航天员训练及出舱活动中的体力负荷和骨肌风险，同时考虑星表低重力步态情况，为航天服设计提供一定参考。