低含液管道内气液两相流动特性的数值研究*

管孝瑞

(中国石化青岛安全工程研究院化学品安全控制国家重点实验室，山东青岛 266071)

0 前言

在天然气气田中，湿气集输工艺被广泛采用，当管道沿程温度、压力发生变化时，饱和水蒸气发生相变生成凝析水，管内进而形成低含液气液两相流动[1-3]。气液两相流动特性的研究对于管线工艺安全、腐蚀防护等具有重要作用[4-5]。气相中夹带的液滴对于管线压降和持液率影响很大[6]。液相分布、剪切力分布等可以用于预测不同部位的冲刷风险[7]。CFD数值模拟软件能够实现对多相流动细节的实时分析[8-16]。潘晓慧等[17]利用数值模拟分析了除尘器入口弯管内气固两相流动。郝雅洁等[18]利用数值模拟对折流板除雾器内气液两相流运动进行了研究，并获得不同粒径液滴的捕集规律。Mito等[19]借助数值模拟对管道环状流内液滴沉积机制进行了详细研究。

目前，对于低含液管路内液滴群的运动行为报道较少。作者在前期实验中，利用修正的弗劳德数和液相韦伯数两个无量纲准则数，依据相似准则搭建了实验管道[2]，本文将借助Fluent 14.5软件对实验管道不同截面内气相流场、液滴空间分布进行了详细地分析。

1 几何模型与网格划分

1.1 几何模型

管道尺寸如图1所示，管径d为90 mm，包含上下两个水平管、上下两个90°弯头、一个竖直管。其中上水平管长度为4 000 mm，弯头曲率半径Rc为120 mm，竖直管长度为630 mm，下水平管长度 为6 000 mm。气液两相由上水平管进入，经上水平管、上弯头、竖直管、下弯头，由下水平管流出。坐标原点位于管道入口，重力沿Y轴负方向。

图1 数值模拟中管路尺寸

1.2 网格划分

为了准确模拟近壁面处的流动情况，采用边界层网格，第一层网格高度ds为35 μm，层间增长因子为1.5，设置12层边界层网格，总厚度为9.012 2 mm。管道横截面网格采用pave生成，总网格数为922 955。管道横截面网格、边界层网格和弯头处网格如图2和图3所示。

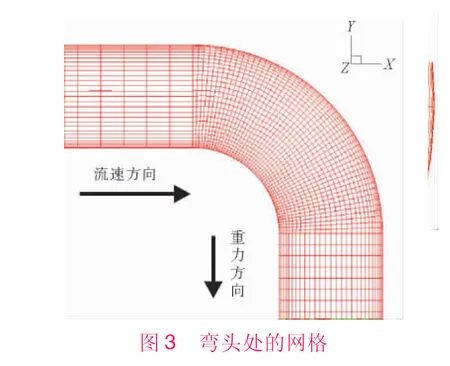
2 计算模型

2.1 湍流模型

湍流是一种高度复杂的不规则、非线性流动状态。RNGk-ε模型[20]能够较好地模拟二次流，数值计算采用RNGk-ε模型来模拟湍流。

2.2 双流体模型

多相流模型选用Eulerian模型，该模型是Fluent中最为复杂的多相流模型，能够对气液两相流动进行精确的模拟。

2.3 边界条件

2.3.1入口条件

采用速度入口条件，其它参数如表1所示。含液率为4.2×10-4。入口设置在上水平管进口截面，气相为主相，液相为第二相。

液相以液滴群形式进入管道，粒径分布与实验管路中入口液滴相一致[2]，如图4所示，比表面积平均粒径d32为109.785 μm，最小粒径为37.028 μm，最大粒径为191.203 μm。

表1 数值模拟计算参数

图4 管路入口液滴粒径分布

2.3.2出口条件

下水平管长径比为67，能够保证管路内气液两相流动充分发展，出口采用自由出流(outflow)边界条件。

2.3.3壁面条件

壁面采用增强壁面函数[21]来处理。模拟最终结果显示y+<5，如图5所示，满足增强壁面函数使用要求。

2.4 计算方法

图5 管道壁面y+值分布

采用有限体积法对控制方程进行离散，应用Phase Coupled SIMPLE格式的压力速度耦合，并应用QUICK格式求解体积分数，连续性方程、动量方程、湍动能方程、湍流耗散率方程采用二阶迎风格式求解。

3 模拟可靠性验证

Nikuradse[22]通过总结大量的实验数据，得到圆管断面流速分布曲线。湍流分为粘性底层、过渡层、对数区[23]。湍流内各区域速度分布分别对应图6中实验曲线1、2、3。水平管分析截面(X=3 150 mm)距离入口3.15 m(35倍管径)，距离下游弯头0.85 m(9.4倍管径)，与入口的距离大于20倍管径，满足流动充分发展要求。为对管道流场进行验证，取该截面上半部从壁面到管中心的流速分布与尼古拉兹流速分布进行对比，结果显示，模拟值和实验值拟合趋势一致，最大偏差为7.15%。

图6 水平管X=3 150 mm处流速分布与实验数据对比

4 结果与讨论

4.1 上弯头内气相流场

上弯头30°截面内气相流线如图7所示，图中红色箭头方向为离心力方向，指向弯头外侧，重力沿半径方向的分量指向弯头内侧，通过比较可知离心力大于重力沿半径方向的分量，因此合力方向指向弯头外侧，造成中心气相由弯头内侧流向弯头外侧。同时由于气相的连续性，两侧壁处的气相由弯头外侧流向弯头内侧。

图7 上弯头30°截面内气相流线

4.2 上弯头后的竖直管内气相流场

图8为上弯头后的竖直管Y=-290 mm截面内气相流场。由于上游弯头内存在二次流，气相进入竖直管后，二次流影响依然存在，竖直管横截面存在一对涡核。

图8 上弯头后的竖直管Y=-290 mm截面内气相流场

4.3 下弯头内气相流场

下弯头内不同截面处的气相流线如图9所示，红色箭头为离心力方向。下弯头0°截面内气相流场与上游竖直管相似，管道横截面内存在一对涡核。在下弯头30°截面，出现两对涡核，一对靠近壁面，一对靠近管道中心。在下弯头内，离心力方向指向弯头外侧，与重力沿半径方向的分量一致，随着弯头角度的增大，两者合力逐渐增大，壁面处的涡核逐渐加强扩大，而靠近管道中心的涡核则逐渐被压缩，在下弯头90°截面处，管道只存在一对涡核，原有的靠近管道中心涡核则消失。

4.4 整体速度云图与流线

图10为管道整体气相速度云图与流线分布，从图中可以看出，在上下弯头内侧气相速度较大，在弯头外侧气相速度较小。在上水平管气相主要沿轴向流动，进入上弯头后，流线开始偏转，竖直管内螺旋前进，经过上下弯头反向运动的不稳定涡流作用后，下水平管也呈现不规则、螺旋流动特征。

4.5 不同截面处的液滴平均体积分数分布

图11为水平管X=3 150 mm截面处的液滴平均体积分数分布，受重力影响，水平管内液滴群主要集中在管道中下部区域，且在靠近管道底部区域具有较高浓度的液滴。

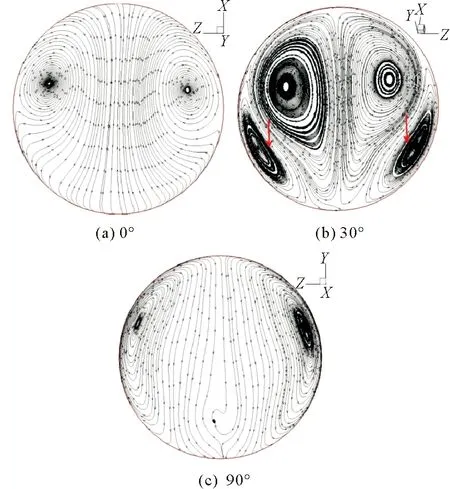
图9 下弯头内气相流线

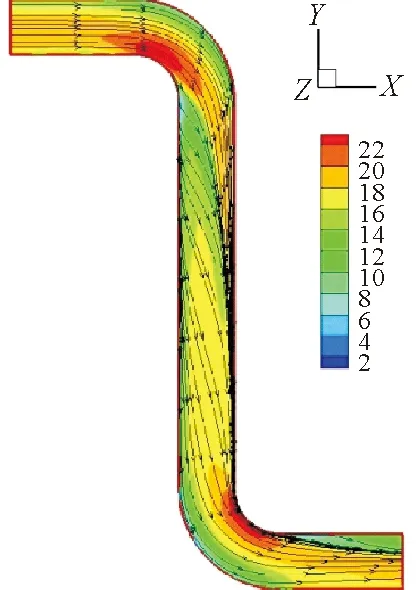
图10 管道整体速度云图与流线

图11 水平管X=3 150 mm液滴平均体积分数分布

图12为上弯头不同截面处液滴平均体积分数分布，液滴群进入弯头后，离心力促使液滴群向弯头外侧运动，与此同时，重力沿半径方向的分量阻碍液滴群向弯头外侧运动。随着弯头角度的增大，重力沿半径方向的分量逐渐减小，与离心力的合力却逐渐增大，促使液滴群逐渐向弯头外侧运动。在上弯头30°截面处，液滴群离开弯头内侧，进入上弯头60°截面时，液滴群到达弯头外侧，在上弯头90°外侧壁面形成较高浓度的液滴群。

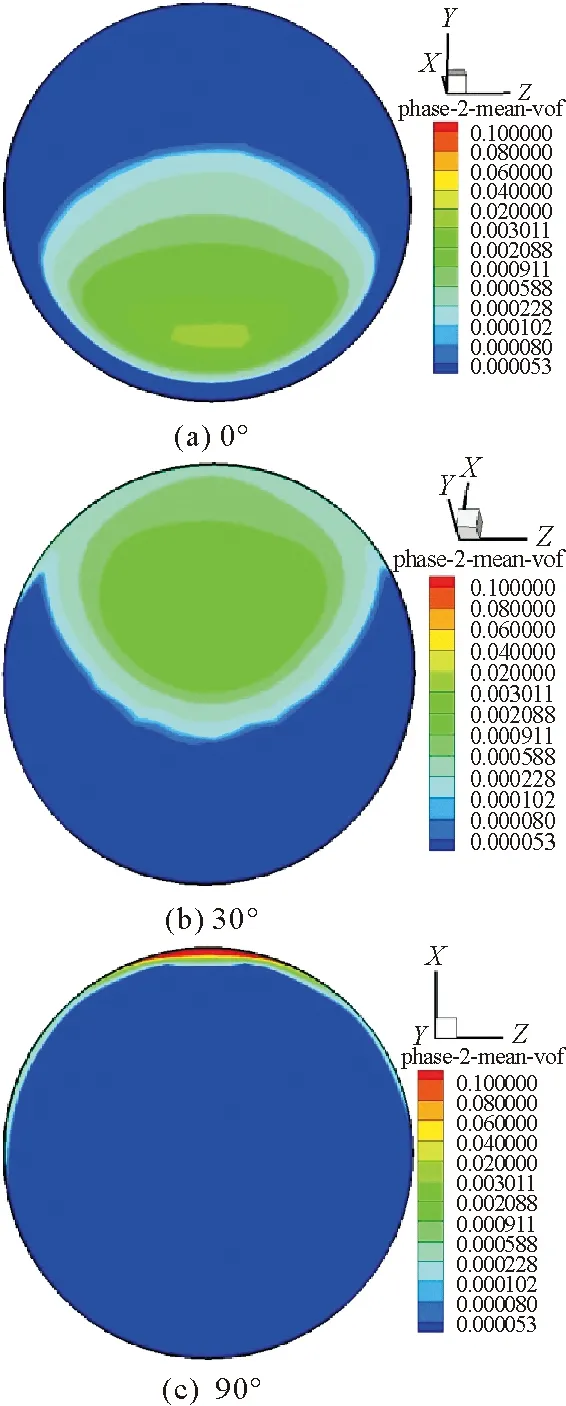
图12 上弯头不同截面处液滴平均体积分数分布

图13为竖直管内液滴平均体积分数分布。受上弯头影响，竖直管内液滴群主要集中在右侧(迎流侧)，与上弯头90°截面分布位置较为一致。但对比Y=-290 mm与Y=-421 mm截面，可以发现，随着与上弯头距离的增大，管内二次流的强度有所减弱，使得竖直管右侧壁面液滴群浓度下降，液滴群分布范围变大，有向左侧运动的行为。

图14为下弯头不同截面内液滴平均体积分数分布，在下弯头内，离心力与重力沿半径方向分量的方向一致，共同促使液滴群向下弯头外侧运动。受上游二次流的影响，在下弯头30°截面处，液滴群主要处于偏向弯头内侧的区域，随着弯头角度的增大，离心力与重力沿半径方向的分量的合力逐渐增大，液滴群逐渐向外侧区域运动，到达下弯头90°时，在外侧形成较高浓度的液滴群。

图13 竖直管内液滴平均体积分数分布

图14 下弯头不同截面内液滴平均体积分数分布

图15为下水平管不同截面内液滴平均体积分数分布。液滴群主要集中在中下区域，且在管道底部具有较高浓度的液滴。但对比X=5 000 mm和X=8 000 mm截面，发现X=8 000 mm截面内，管道底部液滴浓度变小，但液滴分布范围变大。湍流促使液滴扩散，分布范围变广。

图15 下水平管内液滴平均体积分数分布

5 结论

a)采用边界层网格与增强壁面函数相结合的方法，很好地模拟了靠近壁面处的流场。

b)上弯头后的竖直管内存在一对涡核。

c)水平管内液滴群主要集中在中下部区域。弯头内离心力促使液滴群向弯头外侧运动，在弯头90°外侧形成较高浓度的液滴群。受上弯头的影响，竖直管内液滴群主要集中在右侧(迎流侧)，且沿流动方向，右侧液滴群浓度下降，液滴群分布范围变大。