储罐池火特性研究进展*
2019-03-06张日鹏赵祥迪袁纪武马浩然
张日鹏,赵祥迪,王 正,袁纪武,马浩然
(中国石化青岛安全工程研究院化学品安全控制国家重点实验室,山东青岛 266071)
随着石油化工行业的蓬勃发展,储罐的数量和体积急剧增加,储罐内的燃料都具有易燃易爆的特性,而明火、雷击、静电和硫化亚铁自燃都有可能成为火源[1],因此,储罐火灾事故频频发生;而在众多的储罐火灾事故当中,储罐池火灾事故又占了很大比重。为了能更好地对储罐区进行安全评估、制定罐区池火灾事故应急预案、确定储罐之间的安全距离以及确保灭火作业时人员安全和设备的可操作性,需对储罐池火的特性进行研究。
国内外专家对储罐池火特性进行了大量研究,主要集中在燃烧速率、火焰形态(包括火焰高度、火焰倾斜和拖曳)、火焰脉动频率、热辐射通量[2]等参数。本文对储罐池火特性参数的半经验公式进行总结和对比研究。
1 燃烧速率
储罐油品的燃烧由油品蒸发和蒸气燃烧两部分组成[3]。油品燃烧,释放出热量,未燃油品通过辐射或对流从火焰吸收热量,通过传导与储罐进行热量交换;开始阶段未燃油品吸收的热量大于损失的热量,未燃油品温度升高并蒸发加剧,燃烧速率逐渐增加;一段时间后,未燃油品吸收的热量等于损失的热量和蒸发需要的热量,蒸发速率趋于稳定,此时为稳定燃烧阶段,燃烧速率基本保持不变;当燃料产生的热量不足以维持该燃烧状态进行下去时,燃烧进入衰减阶段,燃烧速率和温度逐渐下降。
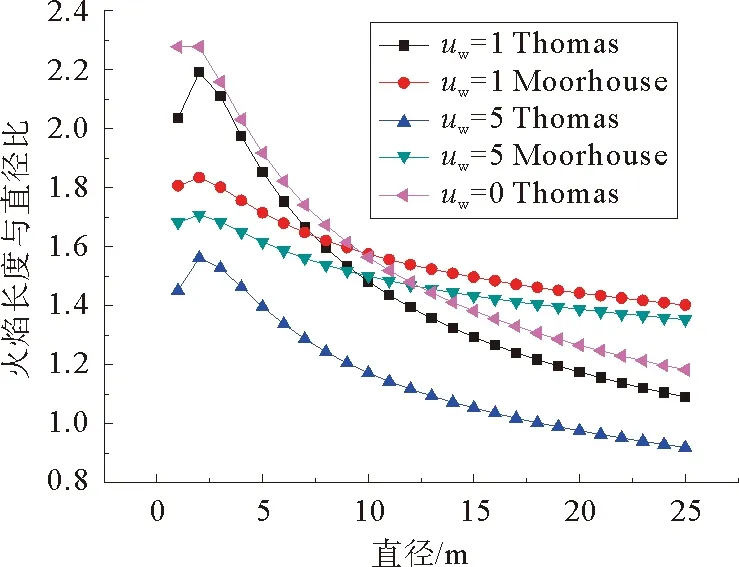
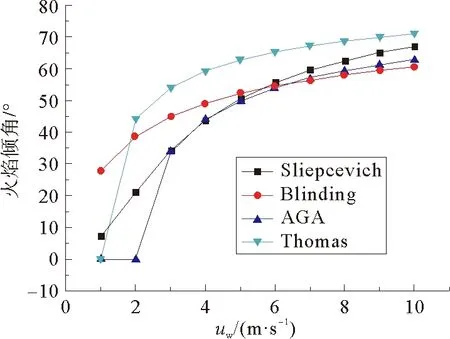
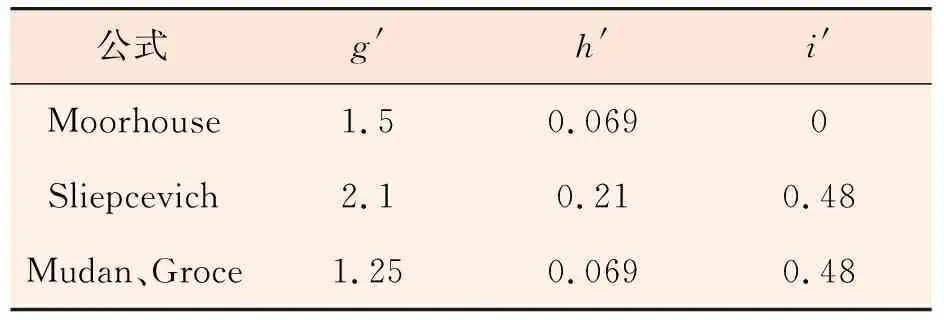
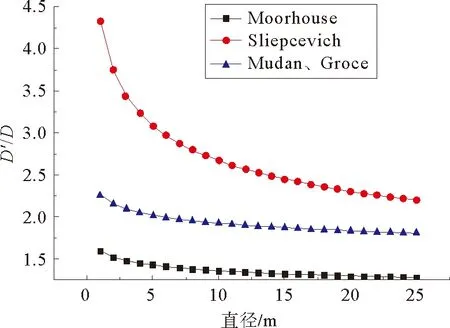
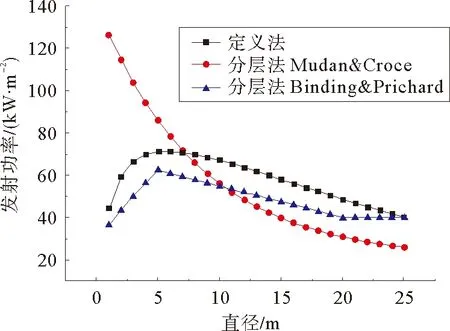
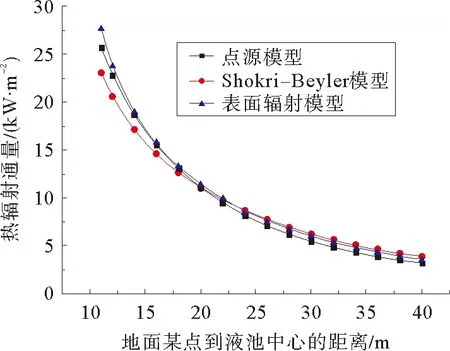
Blinov和Khudiakov通过实验得出:在D<0.03 m时,燃料为层流燃烧,随着储罐直径的增加,燃烧速率下降;在D>1 m时,燃料为湍流燃烧,燃烧速率是常数,与储罐直径和燃料类型无关;在0.03 m 直径>1 m罐,Burgess等认为线性燃烧速率为: (1) 质量燃烧速率m等于线性燃烧速率与密度乘积,如密度不可得,则可通过式(2)估算: (2) 式中:y——线性燃烧速率,m/s; ΔH——燃料燃烧热,kJ/kg; ΔH*——改进的燃料蒸发吸收热,kJ/kg。 公式(1)和(2)都是建立在“池火稳定燃烧时燃烧速率等于蒸发速率”的基础之上,然后通过实验数据确定前面系数得出;其中,公式(1)与实验结果吻合得更好[5,6]。 如果燃料特性参数未知并且要考虑直径对燃烧速率的影响,可以使用Burgess和Zabetakis提出的经验公式来计算燃烧速率: m=m∞(1-e-kD) (3) 式中:m——质量燃烧速率,kg/(m2·s); m∞——无限大池的质量燃烧速率,kg/(m2·s); D——池火直径,m; k——常数,m-1。 许多学者通过实验确定了不同燃料的m∞和k值[5,6]。对于汽油,使用Babrauskas推荐参数,做出质量燃烧速率随储罐直径变化的关系图,见图1。 图1 汽油燃烧速率随直径的变化规律 从图1可以看出,随着储罐直径的增加,质量燃烧速率先逐渐增加,然后维持不变(其最大值与公式(2)计算结果一致[5]),该变化规律与池火湍流燃烧时燃烧速率随直径变化规律相一致。因此,公式(3)适用于直径大于1 m池火湍流稳定燃烧时,质量燃烧速率的计算;公式(2)适用于储罐直径大于2 m时稳定燃烧的质量燃烧速率计算。 关于风速对燃烧速率的影响,由于风对燃烧过程的影响极为复杂,因此,大多数热辐射模型在估算燃烧速率时都没有考虑风的影响,而用风对火焰高度的影响来弥补[5,9]。 目前,一般认为储罐池火火焰为圆柱体。火焰形态由火焰直径、火焰高度、火焰倾斜和拖曳构成。 燃烧过程中火焰高度变化很大,一般提到的火焰高度均指平均火焰高度[11]。关于火焰高度的定义有很多,本文的火焰高度采用Zukoski利用间歇率提出的平均火焰高度[4]。 2.1.1不考虑风速 Heskestad[12,13]、Brotz[14]在池火灾实验基础上以及Thomas[15]在木垛实验和量纲分析的基础上提出不考虑风速影响的火焰高度计算公式(4)~(6): (4) (5) (6) 式中:H——平均火焰高度,m; Q——总放热量,kW; ρa——空气密度,kg/m3。 利用上述公式计算轻柴油池火火焰高度,做出火焰高度与直径比(H/D)随直径变化的曲线,见图2。 图2 H/D随储罐直径变化规律 从图2可看出,随着直径的增加,Brotz公式计算的H/D值先减小然后维持不变;Heskestad和Thomas公式计算的H/D逐渐减小。 笔者曾对11.5 m和20.3 m油池进行柴油池火实验,测得火焰高度与直径的比值分别为1.5和1.4,结合文献[3]中池火高度数据,可以得出:Thomas公式与实验结果更符合;同时,在点源辐射模型和Shokri-Beyler辐射模型中多使用Heskestad公式,而在表面辐射模型中多使用Thomas公式;表面辐射模型更广泛地应用于热辐射计算,这也说明了Thomas公式应用更为普遍。 2.1.2考虑风速 Thomas提出有风条件下火焰长度(L)修正公式: (7) Moorhouse[17]基于大尺度LNG池火实验提出了考虑风速的火焰长度公式: (8) 考虑风作用时,轻柴油池火火焰长度随储罐直径的变化规律如图3。 图3 考虑风作用时L/D值随储罐直径变化规律 从图3可以看出,L/D值随着直径的增加先稍有增加然后逐渐减小,最后趋于定值;针对Thomas公式,考虑风作用时计算得出的火焰长度低于不考虑风作用时,并且风速越大,火焰长度越小;不同风速时,L/D值随直径增加而减小的速率基本相等;针对Moorhouse公式,风速越大,火焰长度越小;不同风速时,L/D值随直径增加而减小的速率基本相等,但减小速率小于Thomas公式的减小速率。 考虑风作用时,Thomas公式和Moorhouse公式应用都较广泛,但Thomas公式应用相对更多。 在风的作用下,池火火焰将会倾斜。1966年,Sliepcevich[18]基于小尺度池火实验提出了火焰倾角与弗劳德数Fr以及雷诺数Re的关系式: (9) 同年,Sliepcevich基于实验数据分析得出:a′=3.3,b′=0.8,c′=0.07;1992年,Blinding基于大尺寸LNG池火实验数据分析得出:a′=0.666,b′=0.333,c′=0.117。 Thomas也提出了计算火焰倾角的表达式: cosθ=0.7×(u*)-0.49 (10) AGA(American Gas Association)[19]针对火焰倾斜提出了计算公式: cosθ=1u*≤1 (11) 对于储罐直径20 m的汽油池火,计算风速从1到10 m/s时,火焰倾角变化规律,如图4所示。 图4 火焰倾角随风速的变化规律 由图4可见,随着风速增加,各公式计算得出的火焰倾角都先增加后趋于稳定;其中Thomas公式计算得出的火焰倾角最大;其余3个公式在风速大于3 m/s时,计算结果相近;在风速小于3 m/s时,Sliepcevich和Blinding公式认为,只要有风,火焰就会倾斜,Blinding公式计算得出的火焰倾斜角较大;而AGA公式认为,存在一个临界风速,小于该风速时,火焰不发生倾斜。文献[20]指出,AGA公式计算结果与实际更符合,应用更广[20]。 由于风的作用,火焰基底向下风向移动,而上风向的火焰边缘以及火焰宽度均保持不变,这种现象称为火焰拖曳。现有的热辐射计算模型更多的只考虑了火焰倾斜而没有考虑火焰拖曳。 Moorhouse认为火焰发生拖曳之后,风的方向上直径计算公式如式(12)所示: (12) 式中:D′——火焰在风向上的直径,m; θ——火焰倾角,°。 国外专家通过实验确定了公式(12)中的参数值,见表1。 表1 公式(12)参数取值 计算当风速为5 m/s时,汽油池火的D′/D值随D的变化规律,如图5所示: 图5 D′/D随直径的变化规律 从图5可以看出,随着储罐直径的增加,D′/D值逐渐减小,最后维持为定值;宋雪飞等认为,Moorhouse计算结果与实验更接近,使用广泛[21,22]。 湍流火焰都有脉动的特性,脉动的主要原因是周围空气对火焰的卷吸效应[23],目前常用的脉动频率计算公式主要有以下几个。 Cetegen[24]基于无量纲特征数分析得出脉动频率计算式(13),Pagni[25]通过分析实验数据得出脉动频率的经验计算式(14),Byram[9]通过对函数进行解析求解得出火焰脉动周期与直径的关系(15): (13) (14) π1=t(gD)0.5 (15) 式中:f——火焰脉动频率,s-1; Ta——环境温度,K; π1——火焰脉动周期,s; t——时间常数。 可见,火焰脉动频率与燃料无关,与D-0.5成正比。 假定池火火焰可以用一点源表示,该点源位于火焰的几何中心,并朝所有方向辐射热量。点源模型热辐射通量计算公式如(16)所示: (16) 式中:q——目标点接收到的热辐射通量,kW/m2; l——点源到目标点距离,m; η——辐射分数; θ——目标物体法线方向与点源和目标物体连线的夹角,°。 Shokri-Beyler模型主要基于实验数据得出: q=EF (17) E=58(10-0.00823D) (18) 式中:E——火焰表面发射功率,kW/m2; F——视角系数。 表面辐射模型为了便于建模和计算,假设热辐射是由火焰表面释放,事实上,火焰释放出的热辐射是由整个火焰(包括燃料气体、燃烧产物、烟气颗粒等)产生的,而不仅仅由火焰表面产生,因此表面辐射模型是对复杂三维热辐射问题的二维简化。该模型认为火焰是静止的灰体,火焰之上的烟羽(不可见火焰)辐射也部分考虑。 Mudan首先提出表面辐射模型的计算公式(19): q=τFE (19) 式中:E——火焰表面单位面积的热辐射释放速率,kW/m2。 发射功率计算主要有以下2种方法。 4.3.1定义求解法 发射功率是单位面积热辐射释放速率,采用总热辐射释放速率除以总面积,如公式(20)表示: (20) 4.3.2分层法 火焰分为上下两部分,下部火焰不被烟气遮挡,上部火焰存在被烟气遮挡的情况。Mudan和Croce认为火焰发射功率Em=140 kW/m2,烟气发射功率Es=20 kW/m2,通过对汽油、煤油和JP-5进行池火实验,建议采用公式(21)来计算高分子量烃类有烟气池火的发射功率(其中S=0.12 m-1): Eav=Eme-SD+Es(1-e-SD) (21) Binding和Pritchard提出如下公式: Eav=xlumElum+(1-xlum)Esoot (22) 式中:xlum——火焰表面中发光火焰占的比例; Elum——发光火焰区域最大发射功率,kW/m2; Esoot——火焰非发光区域的发射功率,kW/m2。 文献[4]认为:对于柴/汽油,Esoot=40 kW/m2;在直径小于5 m时,Elum随直径的增加而增加,关系式为:Elumgasline=53.64D0.474,Elumdiesel=28.03D0.877,xlum gasoline=0.45,xlum diesel oil=0.30;当直径大于5 m时,Elum=115 kW/m2,xlum随直径增加而线性减小,直到池直径大于20 m时,xlum=0。 利用上述方法,计算不同直径柴油池火的发射功率,见图6。 图6 发射功率随直径的变化规律 从图6可以看出,随储罐直径的增加,定义法和分层法(Binding&Pritchard)计算得出的发射功率先增加然后减小,分层法(Mudan&Croce)计算得出的发射功率一直减小。当储罐直径大于7 m时,三者相差不大。因此,在计算大型储罐池火灾的发射功率时,三者均广泛应用。 不考虑风的影响,利用上述三种辐射模型,计算直径为1 m和20 m的柴油储罐池火燃烧时,储罐周围的热辐射通量,并作出热辐射通量与距储罐中心距离的关系,见图7和图8。 图7 直径1 m储罐周围的热辐射通量 从图7和图8可以看出,在储罐直径为20 m时,对于与储罐底面处于同一平面的目标物体,点源模型、Shokri-Beyler模型和表面辐射模型的计算值非常相近,三种模型可以通用。 图8 直径20 m储罐周围的热辐射通量 在储罐直径为1 m且目标物体距储罐中心较近时,Shokri-Beyler计算值最大,表面辐射模型计算值居中,点源模型计算值最小;在储罐直径为1 m且目标物体距储罐中心较远时,Shokri-Beyler计算值依然最大,表面辐射模型和点源模型计算值相近,这说明在储罐直径较小时,Shokri-Beyler模型高估了热辐射通量,储罐直径较小且靠近火源时,点源模型由于没有考虑火焰形状而低估了热辐射通量。 a)基于“燃料蒸发速率等于燃烧速率”的燃烧速率计算公式适合于计算直径大于2 m,池火稳定燃烧时的燃烧速率;考虑直径影响的燃烧速率计算公式适合于计算池火湍流燃烧的燃烧速率;风对燃烧速率的影响还没有完全研究清楚,在计算热辐射时一般也没有考虑,还有待于进一步研究。 b)无风作用时,Thomas公式更适合用于火焰高度计算;有风作用时,Thomas公式和Moorhouse公式都可用来计算火焰高度;AGA公式更适合火焰倾斜角的计算;现有的热辐射计算中一般不考虑火焰拖曳,火焰拖曳直径的计算常使用Moorhouse公式。 c)火焰脉动频率与燃料无关,与D-0.5成正比。 d)在储罐直径为20 m时,对于与储罐底面处于同一平面的目标物体,点源模型、Shokri-Beyler模型和表面辐射模型的计算值非常相近,三种模型可以通用。在储罐直径为1 m且目标物体距储罐中心较近时,Shokri-Beyler计算值最大,表面辐射模型计算值居中,点源模型计算值最小;在储罐直径为1 m且目标物体距储罐中心较远时,Shokri-Beyler计算值依然最大,表面辐射模型和点源模型计算值相近,这说明在储罐直径较小时,Shokri-Beyler模型高估了热辐射通量,储罐直径较小且靠近火源时,点源模型由于没有考虑火焰形状而低估了热辐射通量。 e)现有的池火热辐射模型没有考虑风对燃烧速率的影响、火焰脉动、火焰拖曳以及火焰的三维形态,因此,建议通过实验或模拟,进一步探究池火在这些方面的规律,建立更精确的热辐射模型。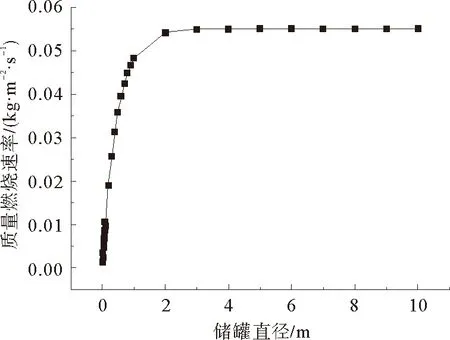
2 火焰形态
2.1 火焰高度
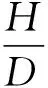
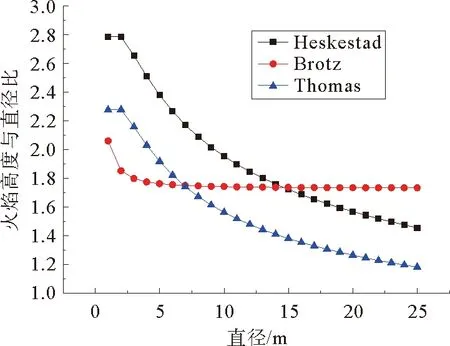
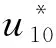
2.2 火焰倾斜
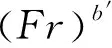
2.3 火焰拖曳

3 火焰脉动
4 热辐射模型
4.1 点源模型
4.2 Shokri-Beyler模型
4.3 表面辐射模型

5 结论
