基于自适应优化的TQWT轴承早期故障诊断方法∗∗

黄慧杰 刘桐桐 任学平

(内蒙古科技大学机械工程学院，内蒙古包头014010)

滚动轴承在旋转机械的应用十分广泛，在设备运行中发挥着无可替代的作用。滚动轴承运行过程中会由于各种原因而发生损坏，轻则产生振动，重则会影响整个机械设备无法正常运行，为了避免引起更大的损失，需要在故障初期对其进行诊断。由于早期故障信息十分微弱，特征提取困难，为此滚动轴承早期故障诊断成为现阶段研究热点以及难点[1-3]。

文献[4]利用小波变换方法处理轴承故障信号，成功的提取出了故障特征；文献[5]利用可调品质因子小波变换分解信号并通过峭度准则以及相关系数准则重构信号，根据重构信号的包络解调谱成功提取出滚动轴承微弱故障特征；文献[6]利用谱峭度最大原则确定可调品质因子小波变换的最佳的共振因子和尺度带，分析重构信号包络谱极值点的频率位置成功提取轴承故障信息。

本文将利用TQWT在不同参数下分解得到的包络谱特征频率强度系数最大原则来提取最优分解分量，通过分析最优分解结果的包络谱来判断轴承故障类型。将通过仿真信号和工程实验数据对本文方法进行验证。为了体现本文方法的优势，将与小波变换方法处理结果进行对比。

1 基础理论介绍

1.1 TQWT

可调品质因子小波变换是早些年由学者Selesnick提出的一种新式离散小波变换。该方法通过改变品质因子Q、过完备系数r以及分解层数J的大小来调节小波分解的尺度因素，十分灵活。TQWT是利用带通滤波器组迭代的方式实现信号分解和重构。以三层分解重构为例，图1为对应的滤波器组分解与重构示意图。

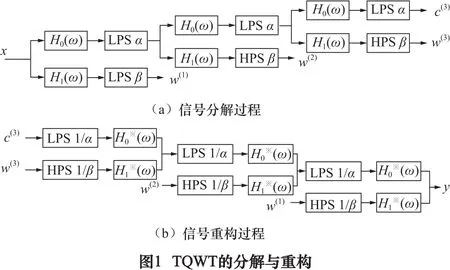
图1中H0(ω)和H1(ω)分别为低通和高通响应函数分别为的复数共轭，α=1-β/r为低通尺度因子，β=2/(1+Q)为高通尺度因子，r为过完备系数。根据文献[7]可以得到滤波器组的中心频率和带宽:

式中:fc和BW分别为滤波器组的中心频率和带宽，fs为信号的采样频率。我们可以通过改变Q、r以及J的大小来调节滤波器组的参数，进而调节TQWT分解效果。

1.2 特征频率强度系数

特征频率强度系数[8]表现为谱图中故障特征频率幅值的明显程度，其定义如下:

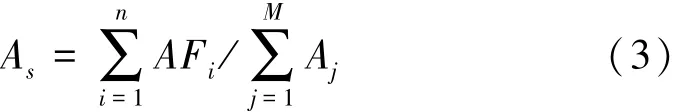
式中:As为特征频率强度系数；AFi为滚动轴承的故障特征频率及倍频对应的幅值大小；Aj为包络谱图中所有的频率的幅值。

特征频率强度系数的大小反映谱图中故障特征频率比重大小，进而反映信号分解效果的好坏。拥有越大的As，信号分解效果越好，故障类型反映到谱图上的效果越清晰。

实际中轴承的故障诊断都是未知故障，需提前将该轴承内圈、外圈、滚动体故障全部计算出来，此时的特征频率强度系数即为每个故障及其倍频对应的幅值之和与全部频率幅值之和的比值。

1.3 改进的TQWT

依靠人工经验选取TQWT的分解参数不仅繁琐而且很难得到最佳的分解效果。本文将对此方法进行改进，自适应的选择得到最优分解结果的参数，其具体步骤如图2所示。

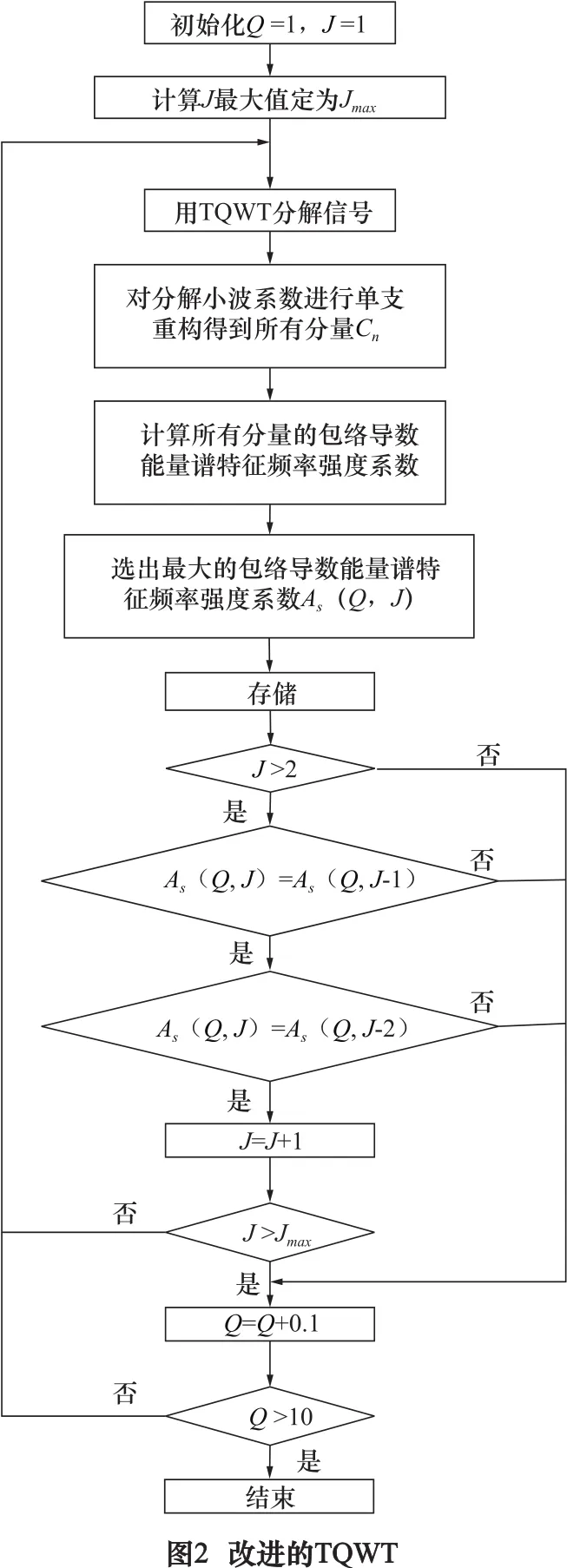
TQWT分解依赖于Q、r、J的值。根据文献[7]我们取r=3，通过调节Q和J的大小来找出最佳的分解效果。

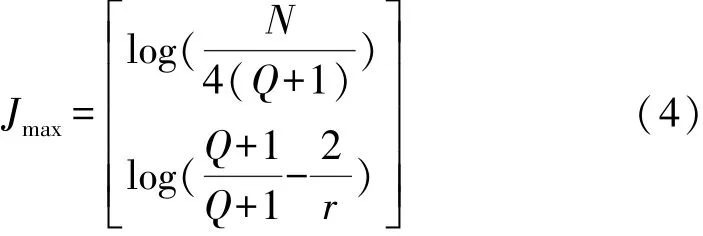
(1)根据公式(4)确定最大的分解层数Jmax。

式中:N为数据长度；[·]为向-∞方向取整。

(2)设置Q=1，J=1，J从 1 到Jmax，步长为 1，进行TQWT分解。分别对每次分解后得到的小波系数进行单支重构并得到一系列的分量Cn。

信号的分解层数J取得过大，在分解得到的前几个分量中，包含主要故障信息的分量已经被分解出来，后续的分解只是多余的，为了减少多余的计算，设置一个提前结束的准则，如果不同分解层数J分解得到最大特征频率强度系数连续三次都一样，则认为更大的分解层数分解信号多余，则提前结束。

(3)Q=Q+0.1，J仍然从 1 到Jmax，步长为 1，重复步骤2，得到相应的特征频率强度系数，直至Q=10结束。

(4)选择特征频率强度系数最大的分量所对应的参数即为最优参数。

1.4 基于改进的TQWT轴承早期故障诊断方法

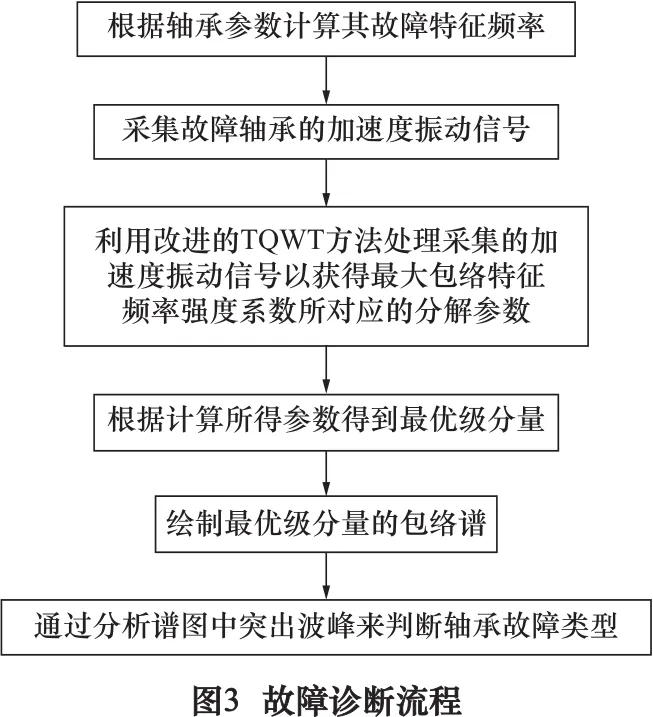
本文对TQWT进行改进，利用包络谱特征频率强度系数筛选最优分解参数，得到最优分解结果，通过分析分解得到的最佳分量的包络谱以确定故障类型，其具体步骤如图3所示。

2 仿真信号分析

根据轴承外圈的故障机理以及其振动数学模型[9-10]，构造包含强噪声的滚动轴承外圈故障振动信号:

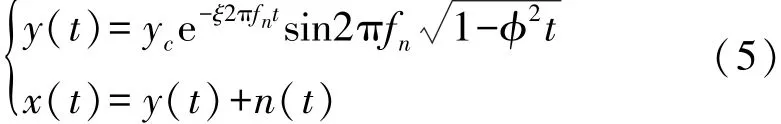
式中:轴承固有频率fn=3 000 Hz，位移常数yc=5，阻尼系数φ=0.1，外圈故障特征频率f0=1/T=180 Hz，n(t)为噪声，添加噪声后信号的信噪比为-10 dB，采样频率fs=20 000 Hz，采样点数N=4 096。

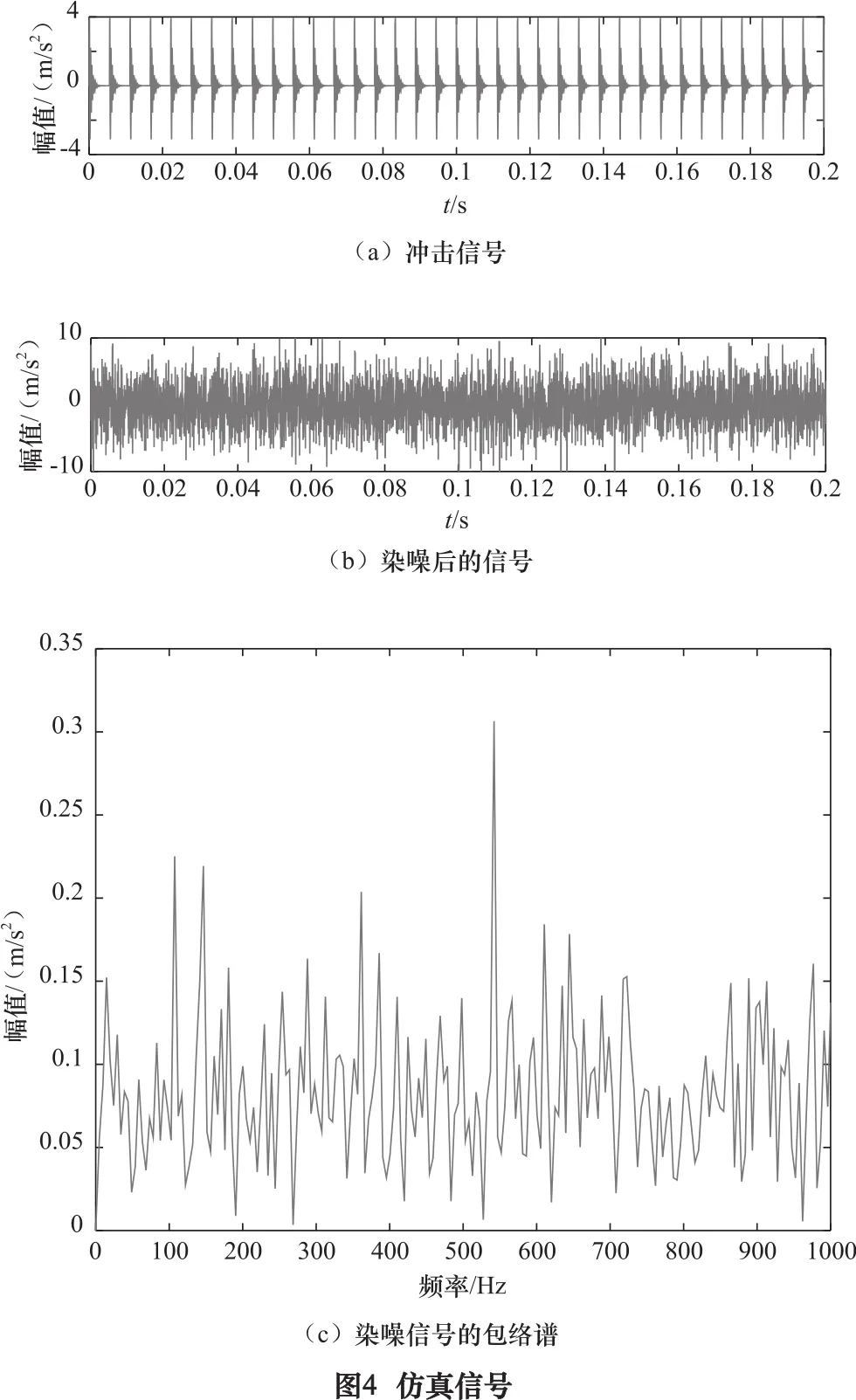
图4a为仿真冲击信号。图4b为添加白噪声后的仿真信号，从图中可以看出，染噪后的信号十分混乱，冲击特征已经完全被覆盖。图4c为染噪信号的包络解调谱，图中并未发现与故障特征频率相对应的突出成分，故障特征已被淹没，传统方法诊断失败。

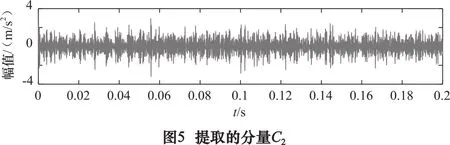
用本文提出的方法计算所有设置参数下TQWT分解得到的包络谱特征频率强度系数，在Q=1.0，J=3时，As取得最大值0.077 7，此时Q、J值即为最优分解参数。设置Q=1.0，J=3，用TQWT对原始信号进行分解，然后对每个小波系数进行单支重构，得到4个分量。其中特征频率强度系数最大的分量为C2，其时域波形如图5所示。

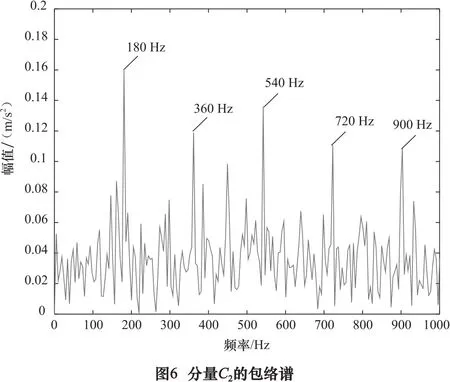
分量C2的包络导数能量谱如图6所示的。谱图中清楚的显示最大峰对应的频率为180 Hz，这与外圈故障特征频率f0相同，其次出现的频率为360 Hz、540 Hz、720 Hz以及900 Hz的峰值分别与故障特征频率的2、3、4和5倍频相对应，至此，本文方法成功提取出了滚动轴承的外圈故障特征信息。

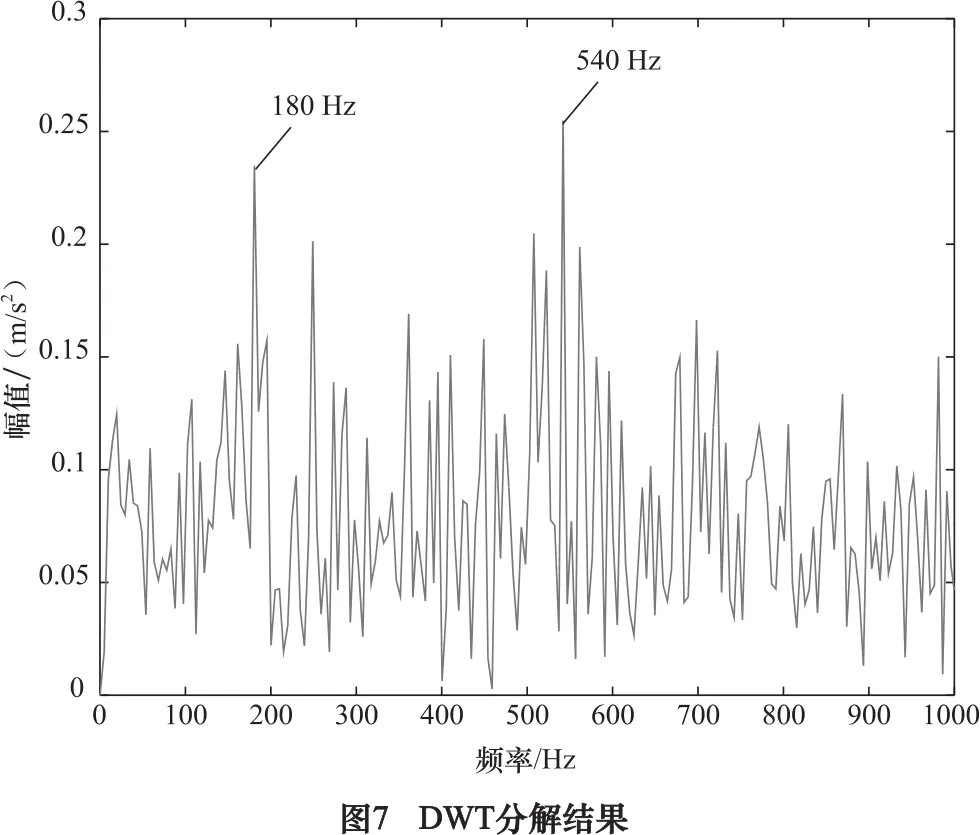
为了体现本文方法的优势，利用DWT(基函数daubechies10小波)对仿真信号进行4层分解并重构，取最大特征频率强度系数0.055 0对应的分量d2，即为效果最好的分量，其包络谱如图7所示。图中只能看到故障特征频率及三倍频，不如图6清晰。

3 实验分析

本实验采用SpectraQuest公司设计的动力与传动故障诊断综合试验台，如图8所示。故障轴承安设于靠近电动机一侧，安装3个加速度传感器于故障轴承所在轴承座上，分别采集垂直、水平、轴向方向的振动加速度信号，并通过DT9837型号数据采集仪存储数据于计算机上。

实验所用轴承型号为ER-16K深沟球轴承，其结构参数如表1所示。

表1 滚动轴承结构参数

模拟轴承外圈故障，实验前轴承内圈、滚动体完好，外圈人为加工轻微凹痕(损伤直径:0.54 mm，损伤深度0.26 mm)作为轴承外圈早期故障。设置采样频率为24 000 Hz，电动机转速为900 r/min(对应旋转频率fr=15 Hz)，采集数据3 s，取16 384个数据点为后续分析。

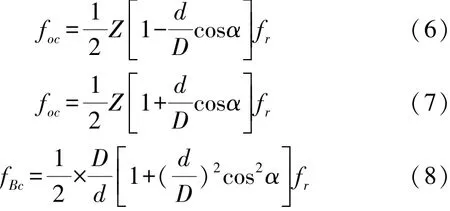
根据公式(6)～(8)计算当前转速下ER-16K滚动轴承的所有故障特征频率如表2所示:

表2 转频15 Hz下滚动轴承故障特征频率

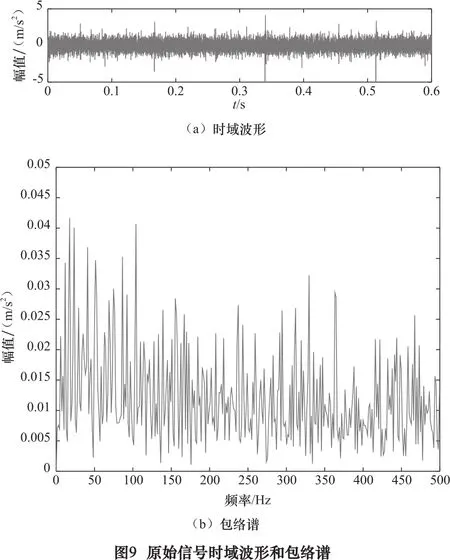
图9a为滚动轴承外圈早期故障信号时域波形，由于噪声干扰严重，无法看出与故障频率对应的周期性冲击。图9b为该信号的包络解调谱，图中并未发现任何突出频率成分，利用传统包络解调法无法对本次试验信号做出精确到故障判断。

利用本文所述方法计算所有参数对应的特征频率强度系数As，在Q=4.5，J=3时，As取得最大值0.083 0，此时Q、J值即为最优分解参数。设置Q=4.5，J=3，用TQWT对原始信号进行分解，然后对每个小波系数进行单支重构，得到了3个分量。

图10是分量C2的包络谱。包络谱中在52 Hz及其倍频处出现了明显的峰值。由于实验电动机转速无法达到预期值，实际值比预期值略小，所以这与理论计算所得的滚动轴承外圈的故障特征频率53.655 Hz相接近，因此，可以确定故障为滚动轴承外圈故障。

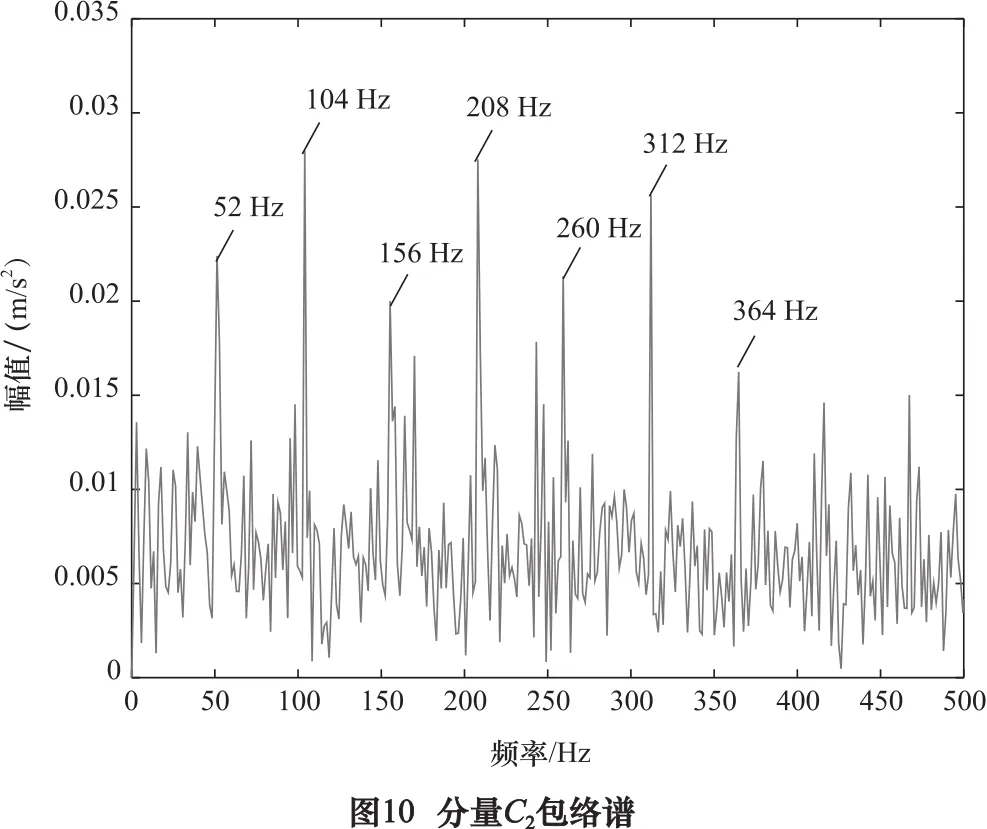
为了体现本文方法的优势，再次利用DWT方法(基函数daubechies10小波)对仿真信号进行4层分解并重构，取最大特征频率强度系数0.066 5分量d1，其包络谱如图11所示。图中频率复杂，干扰频率极多，无法对故障类型进行准确判断。

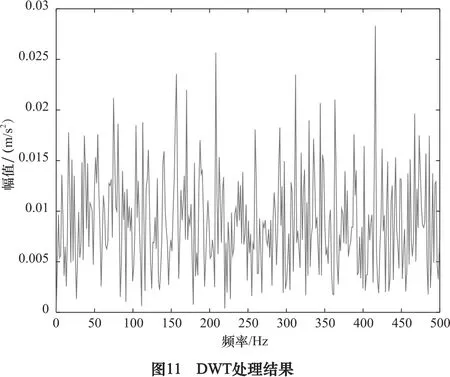
4 结语

传统的可调品质因子小波变换(TQWT)参数选取依赖人工经验，本文将其改进，利用包络谱特征频率强度系数的参数自适应寻优方法来自适应优化TQWT，以得到振动信号的最优分解分量，通过分析最优分量的包络谱来判断轴承的故障类型。经过仿真信号以及工程试验数据验证，该方法能够在传统包络解调法失效的情况下，成功提取出滚动轴承的微弱故障特征；为了体现本文所述方法的优势，通过与传统的小波变换(DWT)分解结果的包络谱相比较，充分证明了本文方法在检测轴承早期故障诊断方面优于DWT。