小学数学教学中运用数形结合思想解决问题案例剖析

■福建省泉州市丰泽区第五中心小学 蔡海兰

作为一种数学思想方法，数形结合的应用大致又可分为两种情形：或者借助于数的精确性阐明形的某些属性，或者借助形的几何直观性阐明数之间某种关系，即数形结合包括两个方面：第一种情形是“以数解形”，而第二种情形是“以形助数”。如何运用数形结合思想，让学生在“画”中学，在学中悟，感悟数学思想方法的价值，体会数学的美、增强学生的数学观念和数学意识，形成良好的思维素质，这是一个值得我们探讨的问题。

一、体验图形在解决问题中的价值

数形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来，通过"以形助数"或"以数解形"即通过抽象思维与形象思维的结合，可以使复杂问题简单化，抽象问题具体化，从而起到优化解题途径的目的。主要指的是数与形之间的一一对应关系。我国著名数学家华罗庚曾说过：“数形结合百般好，割裂分家万事非。”从而可见数形结合在数学的学习中是多么重要。

案例：北师大版六年级上册第二单元《分数混合运算》中“分数混合运算（一）”的学习。在出示例1，明确已知条件和要求后：

1.提问：航模小组有多少人？你是如何思考的。

2.学生独立完成，解决问题。

3.教师重复问题后，要求学生：（1）独立思考，找出单位“1”，画线段图分析数量关系。（2）列出解决问题的算式。（3）与同桌说说自己的解题思路并列式计算。

4.在教师的引导下，借助线段图清楚地表示题目意思及题目中各部分之间的关系。

剖析：分数应用题向来是小学数学学习中的一大难点。如何运用画线段图，提取有价值数学信息、使数量关系明朗化，变得尤其重要。在《数学课程标准》提出的课程目标中，把解决问题作为重要的课程目标，并指出：要使学生面对实际问题时，能主动尝试着从数学的角度运用所学知识和方法寻求解决问题的策略。画图策略是众多解题策略中最基本的、也是一个很重要的策略。在这个知识内容的学习，通过师生共同合作学习，将题目中的三个兴趣小组以下面的这个简要线段图表示出来：

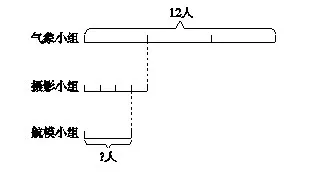
这样一来，学生便能清楚地理解题目中各个量之间的关系，也能容易理解这两种列式的意思。学生通过画线段图这一过程，实践了读题——明确问题——寻找条件——再把文字转化成图画，发现数量关系，最后将图画转成思维，这一系列脑力活动完整地搭建了这个从“外化”到“内化”过程，进一步验证了画图在解决问题中的价值。而这个思维变化的过程会伴随着一些数学思想的渗透，锻炼并提高学生的数学思维能力。

二、运用画图法优化解决问题的策略

学生学会画图，体会画图的作用能促使学生主动应用画图方式来解决问题。

案例：在三年级上册第七单元《一天的时间》中，教学重点是让学生认识24时计时法，并对24时计时法和普通计时法进行换算。

在教学时，如果教师单纯借助时钟进行教学，虽能直观地让学生感受“一天时间”的变化，但在难点上难以突破。如果再辅以“一天有24小时”“为什么是24 小时”“如何记录24 小时”等作为教学的主线，借助学生的经验载体“钟表”，将“一天的时间”半抽象出“时间尺”，借助画图帮助学生建立24时计时法的概念。

剖析：在这部分教学中，显然将“时间尺”这一线段图引入教学能够更准确地把握知识内涵，突破难点。在这一过程中，学生体会借助图还可以解决原本抽象的知识，从而在解决问题策略方面为学生的思考方向开拓出另一个方向。

三、巧用数形结合感受解题策略的多样

在教学中，运用画图的方式体会数形结合思想的优势。并不是只有线段图这一方式，它是灵活多样的，除了线段图外，还有平面图、立体图、集合图、统计图，还包括学生运用自己的方式给出图形表征。在教学中可引导学生根据自己的需要画出不同的图来帮助自己分析、理解数量关系，解决实际问题。

案例：北师大版五年级的《鸡兔同笼问题》。鸡兔同笼，有8个头，26条腿，那么鸡、兔各多少只？如果单从题目的字里行间去理解题意对很多学生来说是一件十分头疼的事。

剖析：不论教师引导学生用假设、方程等各种方法进行学习，相信还是有很多学生对此感到一知半解。但如果引入“数形结合”思想，将本题转化为图形来解决，相信很多学生都能轻松理解。不论是用画“头”装“脚”，还是画“脚”凑“头”等，学生可以根据自己的需要画出不同的图帮助自己分析、理解数量关系，解决实际问题。

四、结语

因此教师应鼓励学生运用多种图的形式来分析和解决问题。着重培养学生数形结合思维（画图策略），使学生能够进行知识及数学思维的迁移，将“画图”策略贯穿于整个小学数学解决问题的教学中。