关于培养高中生数学直观想象素养的教学研究

2019-03-06宁夏育才中学吴必元

天津教育 2019年17期

■宁夏育才中学吴必元

一、情境结合生活实例进行创设

学生在实际学习时，会受到情境的严重影响，一个形象且生动的情境，可以让整个课堂变得更加活跃，同时学生学习的欲望也可以在此状态下被充分激发出来。不断对学生进行促进，使其可以更加积极主动地参与课堂活动，同时也可以将一个自主分析和直观观察以及解决问题的机会提供给每个学生。让学生可以从最初的直观观察逐渐深化到直观想象，有效发展和培养学生的直观想象素养。

针对高中生而言，实际对直观想象素养进行培养时可以通过立体几何进行历练，但是在高中阶段很多学生都会将立体几何作为学习中的难点，甚至有些学生的数学成绩就因为立体几何而无法提高。在立体几何的教学章节中，其中所涉及的内容和生活中常见的几何体有关，因此实际展开此课程教学时，可以将生活中的各种情境有效引入其中，让学生可以更加深刻地认识数学和理解数学以及认同数学，另外数与形之前所具有的联系也可以通过此方式让学生有效把握和认清。

比如学生在刚接触立体几何时，首先，可以选用学生日常生活中比较熟悉的建筑物作为参照，比如金字塔和水立方等，将课本中相关于立体几何的概念引出，这样做不但可以让学生对相关概念的理解得到强化，同时学生内心中的求知欲也可以得到有效激发，不断引导学生从结合的大小和形状以及位置对几何体进行初步认识，然后让学生在此基础上对计算进行探讨，明确几何的绘画及相关应用，让情境的问题驱动有效实现，并更好地将学生大脑中的直观实物激发出来。

二、培养学生的识图能力

高中生学习几何知识时，其中识图能力十分重要，教师实际对学生进行教导时，需要使用各种不同的方式变化解题，只有这样才可以让学生对题目内容的理解进行有效保障，并将题目的相关信息充分抓取住，让学生借助相应的作图和识图以及公式将最终的答案得出。另外，对于教师而言，还需要对学生问题转化能力进行培养，通过图形构建的方式将其逐渐转化成自己所理解的一种方式，并将题目中所隐藏的各种信息有效挖掘出来，让学生在此其概况下可以快速对题目进行转化，并使用更加直观的想象对问题进行解决。

三、应用各种画法解题并构建出最佳问题

学生实际进行解题时，教师可以引导其应用多种画法进行解题，这样不但可以让学生更加快速解题，而且还可以将学生的解题思维提高。实际应用多种画法进行解题时，教师需要最佳问题构建出来，然后在此基础上找到一个图形解题的最佳途径，让学生下次再遇到此类型的习题时可以在最短的时间内找到最合适的画法，并不是在多种画法中选择出某一种较为有效的画法。最开始，教师需对学生进行引导，让学生对几何相关的题目进行观察，然后站在命题人的角度上对此习题的解决方法进行观察，并在此基础上将多样的画法构建出来，在草纸上更加直观地呈现出几何图像，这样的情况对于学生快速掌握解题方法和精准理解相关题意有着十分大的帮助。然后在学生进行解题时，按照自己脑海中所呈现出的图形来解答。比如在解和函数相关的题目时，教师在此情况下就可以引导学生将最优的解题思维构建出来，以此对习题进行解答，让题目中所蕴含的函数知识和几何的相关知识得以有效转化，函数解答的最佳路径应用作图的方式有效实现，以此让学生的解题效率和解题质量得以显著提升，具体如下图所示。

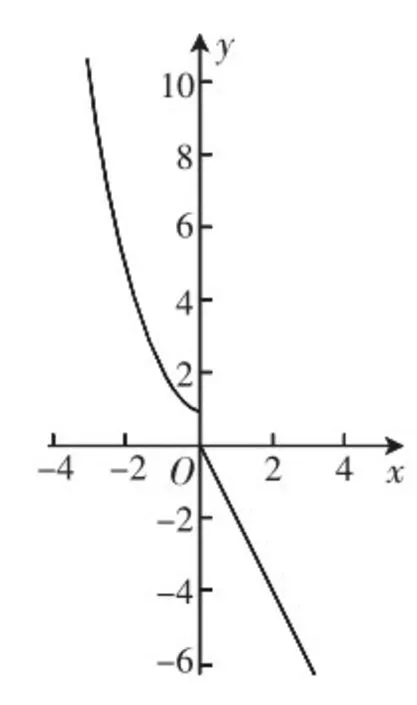
答案：函数f（x）的图像，如上图，由10＞0得f（x）=x2+ 1 = 10，且x＜0，得x=-3。

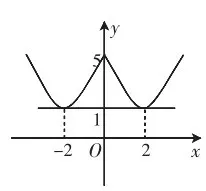
已知关于x方程x2- 4 ||x +5=m有四个不相等的实根，则实数m的取值范围为________。

分析：此习题的解答如果应用直接法，那么则需要先把方程进行化简，然后在此基础上将x1个x2求出，并对其进行详细分类和探讨，然后再加以应用。此过程相对较为烦琐复杂，同时还会导致题目的难度增加。但是如果将二次函数有效地结合起来并将题目图像绘制出来，应用数形结合的方式则可以将此题的解题过程轻松化简，让学生的直观想象力得以充分锻炼。

解：设y1=x2- 4 ||x +5，y2=m，又y1为偶函数，通过上图1＜m＜5可知。