考虑轨道系统的高速铁路连续梁桥结构系统参数对纵向地震响应的影响

杨孟刚，费凡, 2，彭定成



考虑轨道系统的高速铁路连续梁桥结构系统参数对纵向地震响应的影响

杨孟刚1，费凡1, 2，彭定成1

(1. 中南大学 土木工程学院，湖南 长沙 410075； 2. 浙江省交通规划设计院有限公司，浙江 杭州 310006)

为研究无砟轨道系统约束作用下的高铁连续梁桥纵向地震响应，以某组合桥跨布置高铁桥梁结构(2×32 m简支梁+(48+80+48) m连续梁+2×32 m简支梁)为例，针对CRTSⅡ型纵连板式无砟轨道系统的结构特点，建立考虑轨道系统结构层间相互作用的叠合梁模型，研究轨道系统约束作用、地震波激励、滑动层摩擦因数、底座板刚度和制动墩抗推刚度对桥梁结构纵向地震响应的影响。分析结果表明：轨道系统对桥梁结构的约束作用可减弱结构纵向地震响应；在不同频谱特性的地震波激励下，桥梁结构地震响应明显不同，当地震波卓越频率与结构自振频率接近时，将放大结构地震响应；随着轨道系统滑动层摩擦因数增加，连续梁桥纵向地震响应减小，简支梁桥纵向地震响应增强；底座板刚度变化对桥梁纵向地震响应影响较小；增加连续梁桥制动墩抗推刚度，将增强制动墩地震内力响应，需要根据不同抗震需求合理设计桥墩抗推刚度。

高速铁路；连续梁桥；轨道系统；纵向地震响应；结构参数

随着我国高速铁路的发展，无砟轨道被越来越多应用于新建铁路中[1]。对于传统有砟轨道铁路桥梁而言，道砟刚度小离散性大，轨道系统对桥梁结构的约束作用较小，在地震分析时可以忽略轨道系统作用。而无砟轨道纵向刚度较大，尤其当采用CRTSⅡ型纵连板式无砟轨道时，底座板和轨道板纵向联成一体，增强了桥梁结构的整体性和地震响应的耦联性，进行地震分析时不能忽略轨道系统的影响[2−4]。目前，已有学者对于轨道系统对桥梁结构动力特性和地震响应的影响进行了研究。闫斌等[5]研究考虑轨道约束的高铁简支梁桥碰撞响应，结果表明轨道结构约束了桥梁纵向位移，可减弱或消除梁体间碰撞效应；张永亮等[6]以某大跨度连续梁桥为研究对象，讨论轨道系统对桥梁动力特性及地震反应的影响；刘施等[7]以高铁简支梁桥为研究对象，研究不同地震波形、地震烈度对轨道结构纵向力传递规律的影响；史航[8]开展CRTSⅡ型板式无砟轨道高速铁路简支梁桥地震响应分析，结果表明考虑梁轨耦合时桥梁地震动力响应明显减小。CRTSⅡ型板式无砟轨道纵向刚度较大，改变了高铁桥梁动力特性，对高铁桥梁纵向地震响应影响较大[5, 8]。且目前高铁桥梁地震响应研究多以简支梁桥作为研究对象[7−9]，而实际工程中，连续梁桥在跨越既有线路、河道和谷沟时应用更广泛，鉴于此，本文旨在研究考虑CRTSⅡ型无砟轨道系统的高铁连续梁桥纵向地震响应。但是，已有的考虑CRTSⅡ型板式无砟轨道约束的桥梁地震动力响应研究多是将轨道板和底座板视为通过CA砂浆实现协调变形的整体，即道床板[6]。而实际上，轨道板和底座板的弹性模量是CA砂浆层的数倍，三者往往不能实现完全协调变形，轨道板和底座板的力学行为会相互影响[10]。针对上述问题，本文基于ANSYS建立考虑CRTSⅡ型纵连板式无砟轨道系统结构层相互作用的叠合梁模型，研究轨道系统约束、地震波激励、滑动层摩擦因数、底座板刚度和制动墩抗推刚度对高铁连续梁桥纵向地震响应的影响。

1 背景工程

以某连续梁-简支梁桥梁结构(2×32 m简支梁+(48+80+48) m连续梁+2×32 m简支梁)为例，抗震设防烈度为7度，设计基本地震加速度值为0.15。该桥梁结构采用单箱单室截面，材料为C50混凝土，桥面宽12.6 m。连续梁桥中支点梁高为6.72 m，跨中及边支点梁高为3.92 m，梁底按二次抛物线变化。连续梁桥两侧各为2×32 m标准跨径简支梁桥，梁高3.05 m。桥墩为圆端型实体墩，材料为C35混凝土，为消除桥墩高度差异带来的影响将桥墩高度均调整为10 m，基础为钻孔灌注桩。桥梁立面布置如图1所示，桥墩按从左到右依次编号：1号和6号墩为简支梁桥墩，2号和5号墩为连续梁边墩，3~4号墩为连续梁中墩(其中3号为制动墩)。连续梁桥支座采用球型钢支座，简支梁桥采用盆式橡胶 支座。

单位：m

2 CRTSⅡ型轨道系统模拟

CRTSⅡ型纵连板式无砟轨道体系主要构件包括60式钢轨、扣件、轨道板、底座板、砂浆调整层、滑动层、挡块、固结机构和挤塑板等。在台后路基上设置有包括滑动层、端刺和摩擦板等台后传力体系。目前，大多文献在模拟CRTSⅡ型无砟轨道时将轨道板、CA砂浆层和底座板视为一个整体[6]，无法模拟结构层间相互作用及耦合效应。因此，本文模拟CRTSⅡ型纵连板式无砟轨道体系各结构层的力学特性和相互作用，各结构层建模及连接方式如图2所示，模型中部分参数取值如下。

扣件为WJ-8型小阻力扣件，纵向阻力在无载时为13 kN/m/轨，塑性非线性临界点为0.5 mm，竖向刚度为50 kN/mm[11]。根据博格公司试验数据，单位长度CA砂浆层纵横向刚度为128 MN/m，塑性非线性临界点为0.5 mm，竖向抗压刚度为2×106MN/m。滑动层采用理想弹塑性弹簧模拟，弹塑性临界点取为0.5 mm，摩擦因数取为0.2[12]。高强挤塑板仅考虑其竖向刚度，竖向弹性模量取为515 MPa。剪力齿槽采用纵向线弹簧模拟，刚度为1.0×107kN/m[6]。台后传力锚固体系中，摩擦板长度取为50 m，将摩擦板视为与大地固结，大端刺对底座板的纵向限位作用采用线性弹簧单元模拟，弹簧刚度每线取为1.0×107kN/m[13]。

根据上述模拟方式，基于背景工程建立ANSYS有限元模型，如图3所示。为模拟路基上轨道系统对桥上轨道结构的约束作用，在模型中两桥台外侧各建立100 m路基及路基上轨道结构。

图2 CRTSⅡ型无砟轨道-桥梁计算模型

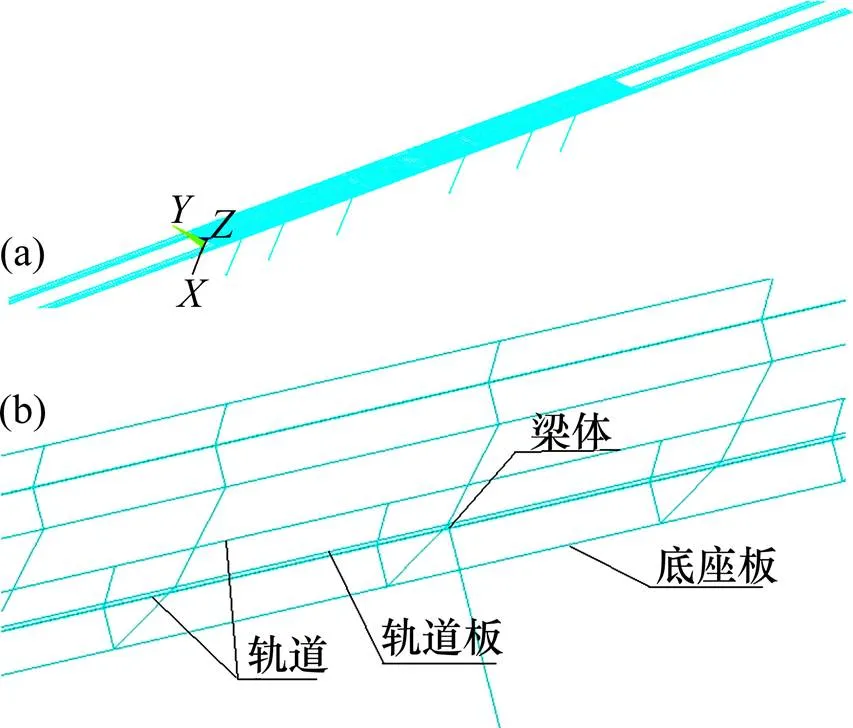
(a) 总体有限元模型；(b) 局部有限元模型

3 轨道系统约束作用分析

为分析轨道系统约束作用对于高铁连续梁桥纵向动力特性的影响，分别建立不考虑轨道系统约束的梁体模型和考虑轨道系统约束的叠合梁模型，其中不考虑轨道系统约束模型二期恒载通过换算为附加质量加于梁顶考虑。表1为2个模型的前5阶自振频率以及相应振型。由表1可知，考虑轨道体系约束后桥梁模型自振频率明显提高。对比表中2种模型的振型可知，不考虑轨道系统时，模型1阶振型为连续梁纵向平动，连续梁和简支梁桥运动关联性不大；考虑轨道系统后，模型1阶振型为连续梁和简支梁桥共同纵向平动，说明无砟轨道系统将连续梁和简支梁桥连接成一个耦合体，增强了结构的整体性。

为进一步探究轨道系统对高铁连续梁桥纵向地震响应的影响，选取调幅至0.15的汶川波对不考虑轨道系统和考虑轨道系统模型分别进行时程分析。表2 是2种模型的纵向动力响应参数峰值之比。其中，3号墩为连续梁桥制动墩，6号墩为简支梁桥制动墩。由表2可知，相比于不考虑轨道系统模型，考虑轨道系统约束的高铁连续梁及简支梁桥桥纵向墩底剪力、墩底弯矩和墩顶位移明显减小，减小幅度最高可到60.1%，说明无砟轨道系统可以减小桥梁纵向地震反应。这是因为无砟轨道系统加强了桥梁结构的整体性，约束并减弱了桥梁纵向地震响应。因此，为了真实模拟高铁桥梁实际地震反应，本文后续分析中采用的模型均采用考虑无砟轨道系统约束的叠合梁模型。

表1 2种模型自振频率对比

表2 2种模型桥墩纵向动力响应峰值的对比

4 纵向地震响应分析

4.1 地震波频谱特性的影响

基于轨道系统叠合梁模型，沿纵向分别输入=0.15的El-Central波、Taft波和汶川波进行时程分析，以连续梁桥3号墩和3号梁为例，列出不同地震波激励下桥梁纵向地震响应结果，响应包括桥墩纵向墩底剪力、墩底弯矩、墩顶位移、固定支座破坏荷载、固结机构破坏时间和梁体纵向位移等，如表3所示。在El-Central波、Taft波激励下，3号墩纵向墩底剪力、墩底弯矩和墩顶位移均非常接近，纵向梁体位移也比较接近。而在汶川波激励下，与El-Central波激励结果对比，3号墩纵向墩底剪力、墩底弯矩、墩顶位移、固定支座剪力分别减少59.76%，57.65%，43.72%和57.86%，3号梁纵向梁体位移减少了65.74%，这是由于汶川波卓越频率在4~5 Hz之间，而El-Central波和Taft波卓越频率在2.2~2.5 Hz之间，后者与结构第1阶纵向自振频率(2.622 Hz)更接近，使得在El-Central波和Taft波激励下结构动力响应更显著。因此，不同地震波频谱特性会对结构地震反应产生较大影响，特别是当地震波卓越频率与结构自振频率接近时，将放大结构的地震响应。

4.2 滑动层摩擦因数的影响

滑动层是实现梁体与轨道系统纵向传力的重要构件，其摩擦因数取值对梁轨动力相互作用有显著影响。在工程应用中，高铁桥梁滑动层会逐渐磨损老化，使得滑动层摩擦因数逐渐增大，因此，有必要研究滑动层摩擦因数改变对结构抗震性能的影响。基于上述叠合梁模型，分别调整滑动层摩擦因数为0.1，0.2，0.3和0.4，沿纵向输入=0.15El-Central波进行纵向地震响应分析，以研究滑动层摩擦因数对高铁桥梁纵向地震相应的影响。图4是不同滑动层摩擦因数条件下3号和6号墩纵向动力响应峰值对比，表4为3号和6号墩上部结构纵向动力响应峰值。

表3 不同地震波激励下3号墩和3号梁纵向动力响应峰值

表4 不同滑动层摩擦因数条件下3号和6号墩上部结构纵向动力响应峰值

由图4和表4可知，当滑动层摩擦因数从0.1增加到0.4时，连续梁桥3号墩纵向墩底剪力、墩底弯矩和墩顶位移分别减少了40.35%，42.14%和42.13%，固定支座由破坏转变为正常工作且剪力明显减小，3号纵向梁体位移减少了72.59%，固结机构破坏时间后延。而简支梁桥随着滑动层摩擦因数的增加，6号墩纵向墩底剪力、墩底弯矩、墩顶位移和固定支座剪力分别增大了39.64%，36.30%，35.15%和37.54%，简支梁桥5号梁纵向梁体位移和固结机构剪力分别增大了38.79%和35.14%。这是因为滑动层摩擦因数的增大加强了高铁桥梁结构体系纵向约束，使得地震能量在连续梁−简支梁桥结构体系的分布发生变化，减弱了连续梁桥纵向地震响应，增强了简支梁桥纵向地震响应。因此，在评估长期运营后的高铁桥梁抗震性能时，需要考虑滑动层老化摩擦因数增大对桥梁纵向地震响应带来的影响。

4.3 底座板刚度的影响

底座板是CRTSⅡ型板式无砟轨道系统主要的受力构件，采用轴向拉压杆件模拟。现分别调整模型底座板刚度为0.8，0.9，1.0和1.1倍原刚度，沿纵向输入=0.15的El-Central波，研究不同底座板刚度对高铁连续梁桥纵向地震响应的影响。图5是不同底座板刚度作用下3号和6号墩纵向动力响应峰值对比，表5为3号和6号墩上部结构纵向动力响应峰值。

图4 不同滑动层摩擦因数条件下3号和6号墩纵向动力响应峰值

表5 不同底座板刚度作用下3号和6号墩上部结构纵向动力响应峰值

由图5和表5可知，当底座板刚度从原刚度的0.8倍变化到1.1倍时，连续梁桥3号墩纵向墩底剪力、墩底弯矩、墩顶位移和固定支座剪力减少了5.30%，5.29%，5.83%和5.32%，3号梁纵向梁体位移减少了5.83%，固结机构破坏时间不变；简支梁桥6号墩纵向墩底剪力、墩底弯矩、墩顶位移和固定支座剪力减少了9.61%，4.32%，2.38%和3.74%，5号梁纵向梁体位移减少了2.38%，固结机构剪力增大16.23%，说明随着底座板刚度的增大，连续梁桥和简支梁桥多项纵向地震响应参数略有减小。这是由于底座板刚度的增大提高了轨道系统整体刚度，从而使轨道系统承担更多地震能量，但与桥梁结构相比轨道系统刚度仍很小，因此增大底座板刚度能在一定程度上减小桥梁结构纵向地震响应，但减小幅度不大。

4.4 桥墩抗推刚度的影响

桥墩作为桥梁结构重要的传力构件，其动力特性对体系动力响应影响很大。现分别调整连续梁桥制动墩3号墩纵向抗推刚度为原刚度的0.6，1.0，1.4和1.8倍(其他桥墩保持不变)，沿纵向输入= 0.15的El-Central波激励进行时程分析，研究制动墩抗推刚度对高铁连续梁桥纵向地震响应的影响。图6是不同抗推刚度条件下3号和6号墩纵向动力响应峰值对比，表6为3号和6号墩上部结构纵向动力响应峰值。

由图6和表6可知，随着连续梁桥3号制动墩抗推刚度从原刚度的0.6倍增加到1.8倍，连续梁桥3号墩纵向墩底内力响应明显增加，固定支座剪力增大乃至发生破坏，而纵向墩顶位移和梁体位移迅速减小，梁上固结机构破坏时间后延。简支梁桥多项地震响应参数变化不大。上述结果说明，增加连续梁桥制动墩抗推刚度，将改变连续梁桥结构体系地震能量分布，使制动墩承担更多地震能，从而减小了上部结构地震响应。因此，在对桥墩进行抗震设计时要合理选择制动墩抗推刚度。

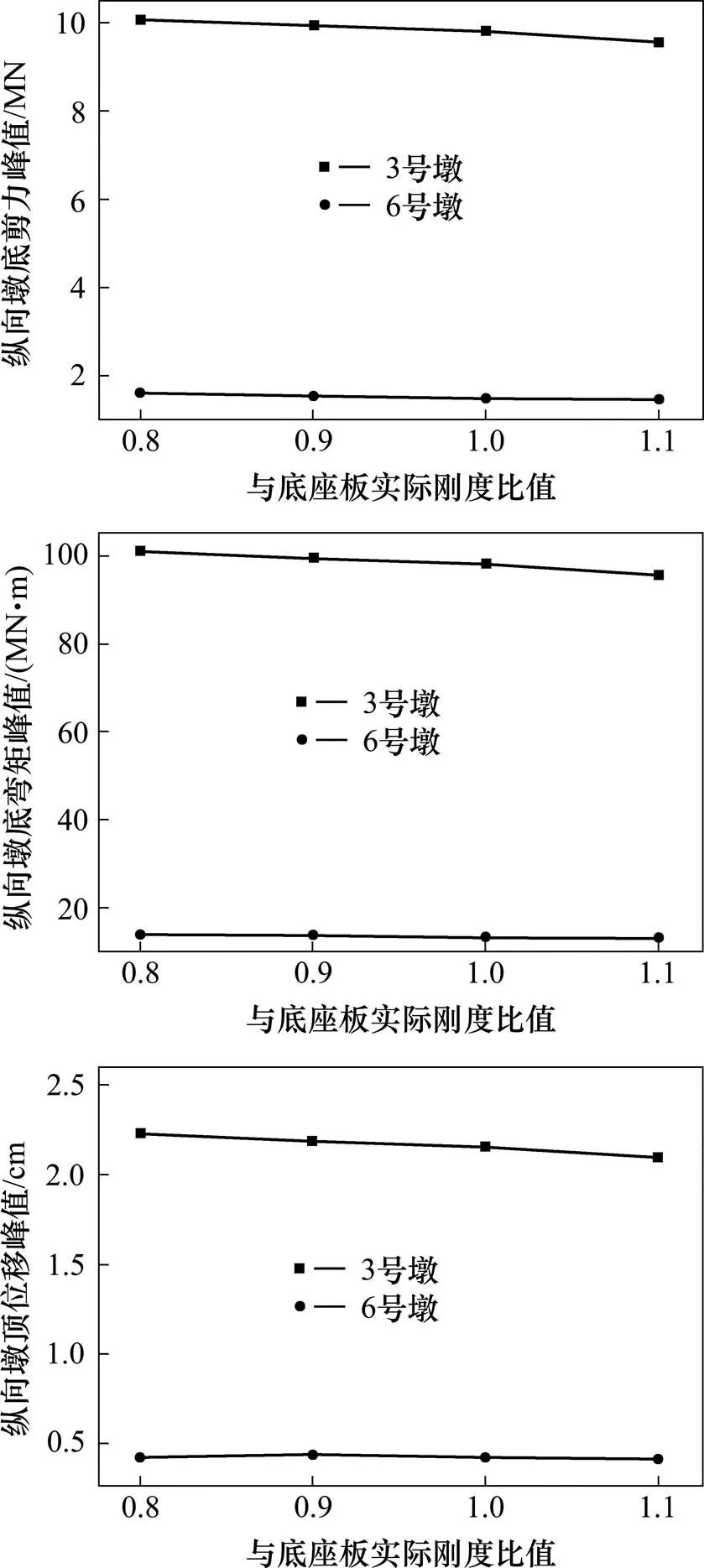
图5 不同底座板刚度作用下3号和6号墩纵向动力响应峰值

图6 不同桥墩抗推刚度条件下3号和6号墩纵向动力响应峰值

表6 不同桥墩抗推刚度条件下3号和6号墩上部结构纵向地震响应峰值

5 结论

1) CRTSⅡ型纵连板式无砟轨道体系能够增强高铁桥梁结构纵向刚度，将多跨桥梁结构连接成一个耦合体，增强了结构体系的整体性，改变了结构体系的动力特性，使得桥梁纵向地震响应减弱。在进行地震响应分析时若不考虑轨道系统约束，会高估高铁桥梁结构纵向地震响应，不能真实反映结构体系的动力响应。因此，在进行地震响应分析时需要考虑轨道系统的影响。

2) 结构地震动力响应与地震波频谱特性联系密切，在不同卓越频率的地震波激励下，高铁连续梁桥纵向地震响应明显不同。当地震波卓越频率与结构自振频率接近时，将放大结构地震响应。

3) 随着滑动层摩擦因数的增大，高铁连续梁桥纵向地震响应减弱，简支梁桥纵向地震响应增强。评估长期运营后的高铁桥梁抗震性能时，需要考虑到滑动层摩擦因数变化带来的影响；增大底座板刚度能在一定程度上减小桥梁结构纵向地震响应，但减小幅度不大。

4) 增加连续梁桥制动墩抗推刚度，使制动墩地震内力响应增加，而上部结构地震响应减小，因此，需要根据不同抗震需求合理选择桥墩抗推刚度。

[1] KANG Xin, JIANG Lizhong, YU Bai, et al. Seismic damage evaluation of high-speed railway bridge components under different intensities of earthquake excitations[J]. Engineering Structures, 2017, 152: 116− 128.

[2] Lemura H, Iwata S, Murata K. Shake table tests and numerical modeling of seismically isolated railway bridges[C]// Proceedings of the 13th World Conference on Earthquake Engineering, 2004: 1−15.

[3] 吴青松, 任娟娟, 刘学毅, 等. 用于铺设Ⅱ型板式轨道的大跨连续梁桥合理温度跨度研究[J]. 铁道科学与工程学报, 2016, 13(3): 414−422. WU Qingsong, REN Juanjuan, LIU Xueyi, et al. Research on the critical expansion length of large span continuous beam bridge for CRTSⅡ slab track[J]. Journal of Railway Science and Engineering, 2016, 13(3): 414−422.

[4] 彭定成. 考虑轨道系统的高速铁路连续梁桥纵向地震响应研究[D]. 长沙: 中南大学, 2017. PENG Dingcheng. The research on longitudinal seismic response of high speed railway continuous beam bridges considering the track system[D]. Changsha: Central South University, 2017.

[5] 闫斌, 戴公连, 粟淼. 考虑轨道约束的高速铁路简支梁碰撞效应研究[J]. 桥梁建设, 2014, 44(6): 24−28. YAN Bin, DAI Gonglian, SHU Miao. Study of pounding effect of high-speed railway simply-supported beam bridge considering track constraint[J]. Bridge Construction, 2014, 44(6): 24−28.

[6] 张永亮, 赵继栋, 陈兴冲, 等. 轨道约束对高铁大跨连续梁桥地震反应的影响[J]. 铁道工程学报, 2015, 32(7): 47−50. ZHANG Yongliang, ZHAO Jidong, CHEN Xingchong, et al. Influence of track system restraint on seismic response of the high-speed railway long-span continuous girder bridge[J]. Journal of Railway Engineering Society, 2015, 32(7): 47−50.

[7] 刘施, 闫斌, 张鹏飞, 等. 地震作用下桥梁-CRTSⅡ型无砟轨道相互作用规律[J].铁道科学与工程学报, 2017, 14(4): 669−674. LIU Shi, YAN Bin, ZHANG Pengfei, et al. The embedded CRTSⅡ slab ballastrless track in interaction with bridges under seimic action[J]. Journal of Railway Science and Engineering, 2017, 14(4): 669−674.

[8] 史航. 考虑精细化建模的高速铁路简支梁桥纵向地震反应研究[D]. 长沙: 中南大学, 2015. SHI Hang. The refinement research on longitudinal seimic response of simply supported beam bridges for high speed railway[D]. Changsha: Central South University, 2015.

[9] 杨孟刚, 周卫卫, 乔建东. 基于限位索的简支梁桥地震防碰研究[J]. 地震工程与工程振动, 2015, 35(5): 99− 104. YANG Menggang, ZHOU Weiwei, QIAO Jiandong. Research on using cable restrainers to prevent collision between girders for simple supported bridges under strong earthquake[J]. Earthquake Engineering and Engineering Dynamics, 2015, 35(5): 99−104.

[10] 朱乾坤, 戴公连, 闫斌. 简支梁-CRTSⅡ型板式无砟轨道制动力传递规律[J]. 铁道科学与工程学报, 2014, 11(6): 13−19. ZHU Qiankun, DAI Gonglian, YAN Bin. Transfer law of breaking force between simply-supported bridges and CRTSⅡ slab ballastless track[J]. Journal of Railway Science and Engineering, 2014, 11(6): 13−19.

[11] TB 10015—2012, 铁路无缝线路设计规范[S]. TB 10015—2012, Code for design of railway continuous welded rail[S].

[12] 铁道部工程管理中心. 京津城际轨道交通工程CRTS Ⅱ型板式无砟轨道技术总结报告[R]. 北京: 铁道部工程管理中心, 2008. Engineering Management Center of the Ministry of Railways. Summary report on the technology of CRTS II slab ballastless track for Beijing Tianjin intercity rail transit project[R]. Beijing: Engineering Management Center of the Ministry of Railways, 2008.

[13] 魏强, 赵国堂, 蔡小培. CRTSⅡ型板式轨道台后锚固结构研究[J]. 铁道学报, 2013, 35(7): 90−95. WEI Qiang, ZHAO Guotang, CAI Xiaopei. Study on anchor structure behind the abutment for slab track CRTSⅡ[J]. Journal of the China Railway Society, 2013, 35(7): 90−95.

Influence of structural parameters on longitudinal seismic response of high-speed railway continuous beam bridge considering the track constraint

YANG Menggang1, FEI Fan1, 2, PENG Dingcheng1

(1. School of Civil Engineering, Central South University, Changsha 410075, China; 2. Zhejiang Provincial Institute of Communications Planning, Design & Research, Hangzhou 310006, China)

The longitudinal seismic response of the high-speed railway continuous beam bridge was studied in this paper. A combined type high-speed railway bridge was taken as an analysis example. The bridge system consists of two 32 m simple-supported bridges, one (48+80+48) m continuous-beam bridge and two 32 m simple- supported bridges. The finite element of the example bridge was established, in which the CRTSⅡ slab ballastless track on the bridge was considered. Based on this model, this paper studied the influence of some parameters on bridge longitudinal seismic response, corresponding to the seismic wave spectrum, the friction coefficient of sliding layer, the rigidity of the base plate and the push rigidity of abutment pier. The research has obtained some results. Compared with the no track finite element model, the longitudinal seismic response of the model considering the track system is weakened. The seismic response spectrum has great influence on the bridge seismic response, which will be increased when seismic wave predominant frequency is close to the natural frequency of the structure. With the increasement of the friction coefficient of sliding layer, the seismic responseof the continuous beam bridge is reduced, and the seismic response of the simply supported beam bridges is increased. The stiffness change of the base plate has little influence on the bridge longitudinal seismic response. The increasement of the push rigidity of continuous beam bridge’s brake pier will intensify its force response. Therefore, it is necessary to design pier push stiffness according to the different seismic requirements.

high speed railway; continuous beam bridges; track system; longitudinal seismic response; structural parameters

10.19713/j.cnki.43−1423/u.2019.01.002

U24

A

1672 − 7029(2019)01 − 0008 − 08

2018−01−25

国家自然科学基金资助项目(51378504)；中南大学中央高校基本科研业务费专项资金资助项目(2017zzts754)

杨孟刚(1976−)，男，江西安义人，教授，博士，从事跨度桥梁几何非线性与桥梁抗震研究；E−mail：mgyang@csu.edu.cn

(编辑 阳丽霞)