基于Hydrus-1D的滴灌土壤水分运移数值模拟

徐丽萍，张朝晖

(甘肃省疏勒河流域水资源管理局，甘肃 玉门 735211)

大田试验因其精度较差、耗时及劳动强度大等缺点，越来越多的研究者将精力集中在计算机数值模拟的应用方面，利用模型在众多组合处理中进行初步选择，然后在大田试验中进一步优选和验证成为了农业、水利等科研和技术推广和验证的普遍方法，在土壤水分运动方面主要有模拟田面水流运动的WinSRFR模型，模拟地下水运动及溶质运移的visual modflow及模拟包气带土壤水分运动及溶质运移Hydrus1/2/3D等，其中Hydrus系列软件在模拟土壤水分运动及溶质运移方面因其具有扎实的理论依据和丰富的经典模型得到了广泛的应用，其既可以模拟融雪在土壤中的运动过程(汤英，2011年)，又可以适应不同的灌水方式，如沟灌(张吉孝，2013年)、滴灌(单鱼洋，2012年)、微润灌溉(陈高听等，2016年)等，又可对溶质和污染物的运移进行模拟，包括盐分离子(何康康，2016年)和垃圾填埋场渗滤液中的氨氮(杨洋等，2014年)，也可以将Hydrus软件延伸到灌溉制度的制定和评价(虎胆·吐马尔白，2015年)，这些模拟和应用均取得较满意的结果，说明Hydrus软件在模拟土壤水分运动和溶质运移方面具有较高的精度，本文用Hydrus-1D软件对室内有机玻璃箱滴灌水分运移过程进行了模拟，并对其土壤水力特性参数进行求解，并用均方根误差RMSE和决定系数R2进行评价。

1 模型简介

Hydrus-1D是美国盐土实验室开发的一款计算包气带土壤水分、溶质运移的模型，其数值计算饱和非饱和水流的Richards方程和热传递、溶质运移的对流扩散型方程，主要模块包括主程序模块(main processess)、工程管理(project manager)、几何模块(geometry)、图形模块(graphics)和边界条件(boundary)几部分组成，能模拟包括饱和非饱和土壤水分运动、溶质运移(包括污染物运移)和热运移，并且能考虑根系吸水、根系生长和CO2的影响。可根据实际模拟对象选择上边界条件和下边界条件，当边界条件变化时，可根据其变化条件进行单独设置。在土壤水分运动模型方面提供了单孔隙模型，如V-G模型、修正的V-G模型及B-C模型等，以及双孔隙渗透模型等多种模型可供选择。最后根据graphical editor土壤剖面对模拟区域进行离散化和初始压力水头(含水率)对所定义的过程进行模拟。

Hydrus模型在描述土壤水分运动中有单孔介质模型、双重介质模型等，选择单孔介质模型中的。Van Genuchten模型来模拟滴灌土壤水力特性，V-G模型表达式为：

(1)

(2)

(3)

(4)

式中：θ为土壤体积含水率，cm3/cm3；φm为土壤基质势，cm；θr为土壤残余体积含水率，cm3/cm3；θs为土壤饱和体积含水率，cm3/cm3；α、n、m均为拟合参数；Se为土壤相对饱和度；Ks为土壤饱和导水率，cm/h。

2 试验及模拟

2.1 模拟设计

试验用有机玻璃箱模拟田间滴灌灌水过程中的土壤水分入渗过程，有机玻璃箱长×宽×高尺寸为100 cm×30 cm×100 cm，试验用马氏瓶供水，马氏瓶长×宽×高尺寸为10 cm×10 cm×100 cm，滴头采用贴片式滴头，滴头流量为1.8 L/h，灌水定额为225 cm3/hm2，试验土壤以砂壤土为主，平均容重为1.34 g/cm3，按照田间实际土层分层填装，初始体积含水率8 cm3/cm3。用TDR土壤水分快速测定仪测定0～100 cm土层的土壤含水率，分10层，每层10 cm在灌水前、后测定土壤体积含水率。

2.2 模拟参数

土壤水力学参数的确定根据试验供试土壤容重、土壤机械组成等，土壤残余体积含水率θr、土壤饱和体积含水率θs分别根据烘干称重法、环刀法在实验室进行测定，土壤饱和导水率Ks利用Ku-pF非饱和导水率测定系统进行测定，测定得到的土壤水力学参数如表1所示。

表1 供试土壤水力学参数

试验开始时，滴头以恒定流量q=1.8 L/h进行灌溉，在灌溉开始时，即在t=t0时刻，土壤含水率为初始土壤含水率q0，上边界为表层无积水的大气边界条件，滴灌为局部灌溉，在模拟深度为1 m时，下边界可看做是自由排水边界，不受地下水位的影响，初始条件和边界条件分别为：

初始条件：q(z，t)=q0(z，0)

(5)

(6)

(7)

滴灌是一种典型的三维点源入渗问题，但是其水分在各向同性土壤中的运移可以看做是中心对称过程，因此可以将滴灌入渗过程的模拟简化为二维平面水分运动，则用水势表示的土壤水分运动基本方程可以表示为：

(8)

确定显示差分法计算区域，选取垂直于滴灌带的土壤剖面，垂直方向从地表至100 cm处、水平方向选择正负各15 cm为模拟区域，首先将模拟区域离散化，在Z轴方向将土层划分成101个单元，如图1所示，时间步长为小时，设定最小时间步长为0.001 h，最大时间步长为0.1 h。

图1 模拟剖面离散化(单位：cm)

3 结果与分析

3.1 模型校正与验证

对试验结束后的土壤水分分布进行测定，如图2所示，可以看出其以滴头为中心对称分布，距离滴头越近土壤水分含量越高，灌水完成后土壤水分再分布基本呈椭圆形，在垂向运移距离大于水平方向的运移距离，这可能与土质有关。分别对距离滴头不同位置处的实测的土壤含水率和利用Hydrus模拟的土壤含水量进行对比，对比关系如图3所示。

从图3可以看出，在不同位置处土壤含水率模拟值和实测值的吻合效果比较好，特别是当土壤含水率比较大的滴头处及距离滴头较近的位置，其中图3(a)模拟效果略差，但是整体来说，利用Hydrus软件模拟得到的结果可以接受，可用于实际应用。利用均方根误差RMSE和决定系数评价两者之间的误差关系，其中均方根误差RMSE如下：

(9)

式中：Si为样点土壤含水率模拟值；Oi为样点土壤含水率实测值；n为取样总数。

根据实测的土壤含水率和模拟值进行计算，对水平距离滴头不同位置不同深度处的实测和Hydrus模拟的土壤含水率值进行了均方根误差RMSE计算，计算结果如表2所示。

从表2可以看出对于距离滴头不同位置在不同深度的土壤含水率实测值和模拟值的均方根误差RMSE和决定系数值所反映出的模拟精度都比较高，并且距滴头越近，其模拟效果越好，在滴头位置处RMSE达到0.021 6 cm3/cm3，决定系数R2为0.856 2，所表现出来的拟合精度最高，在距离滴头-15 cm处效果最差，其RMSE为0.190 6 cm3/cm3，决定系数R2为0.657 1，但该结果也能大致反映在滴灌后距离滴头较远位置处的土壤水分分布状况，其他距离滴头-10、10、-5及5 cm等通过评价指标均方根误差RMSE和决定系数R2来看，其模拟结果均较好，其中均方根误差RMSE和决定系数R2的最大值出现在图3(b)中，但是也达到0.067 2 cm3/cm3和0.662 7，该结果可保证一般大田应用。

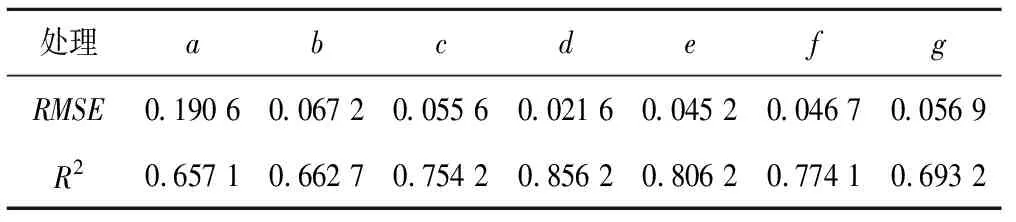
处理abcdefgRMSE0.190 60.067 20.055 60.021 60.045 20.046 70.056 9R20.657 10.662 70.754 20.856 20.806 20.774 10.693 2

3.2 土壤水力特性

土壤水分特征曲线是表征土壤水分能量和数量关系的曲线，对土壤持水性和水分有效性等研究中具有重要的意义，导水率也是反映土壤水分有效性的重要参数，通过Hydrus软件对试验装置土壤的导水率K(cm/h)和水分特征曲线进行模拟，如图4和图5所示。

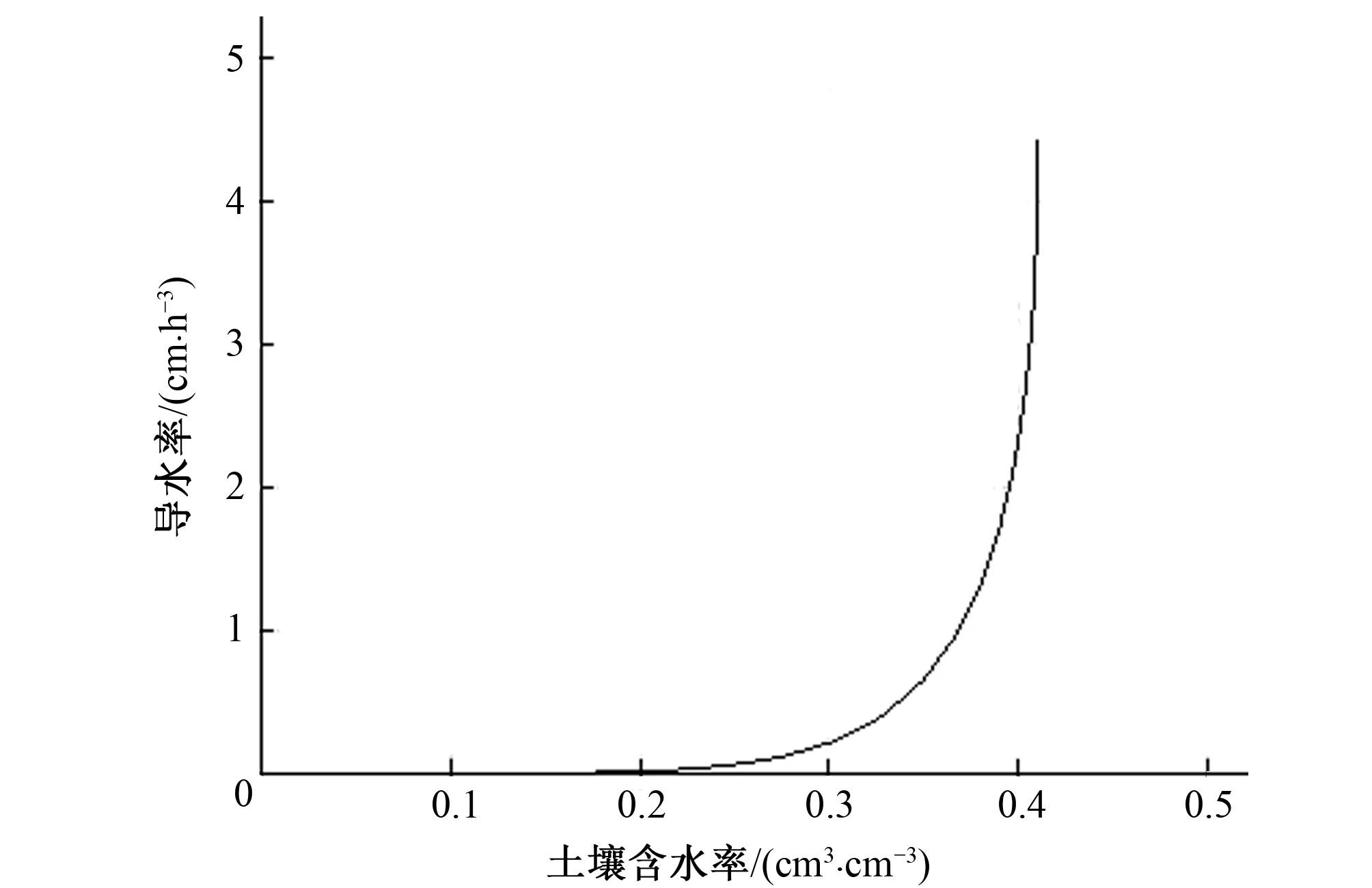
图4 导水率曲线

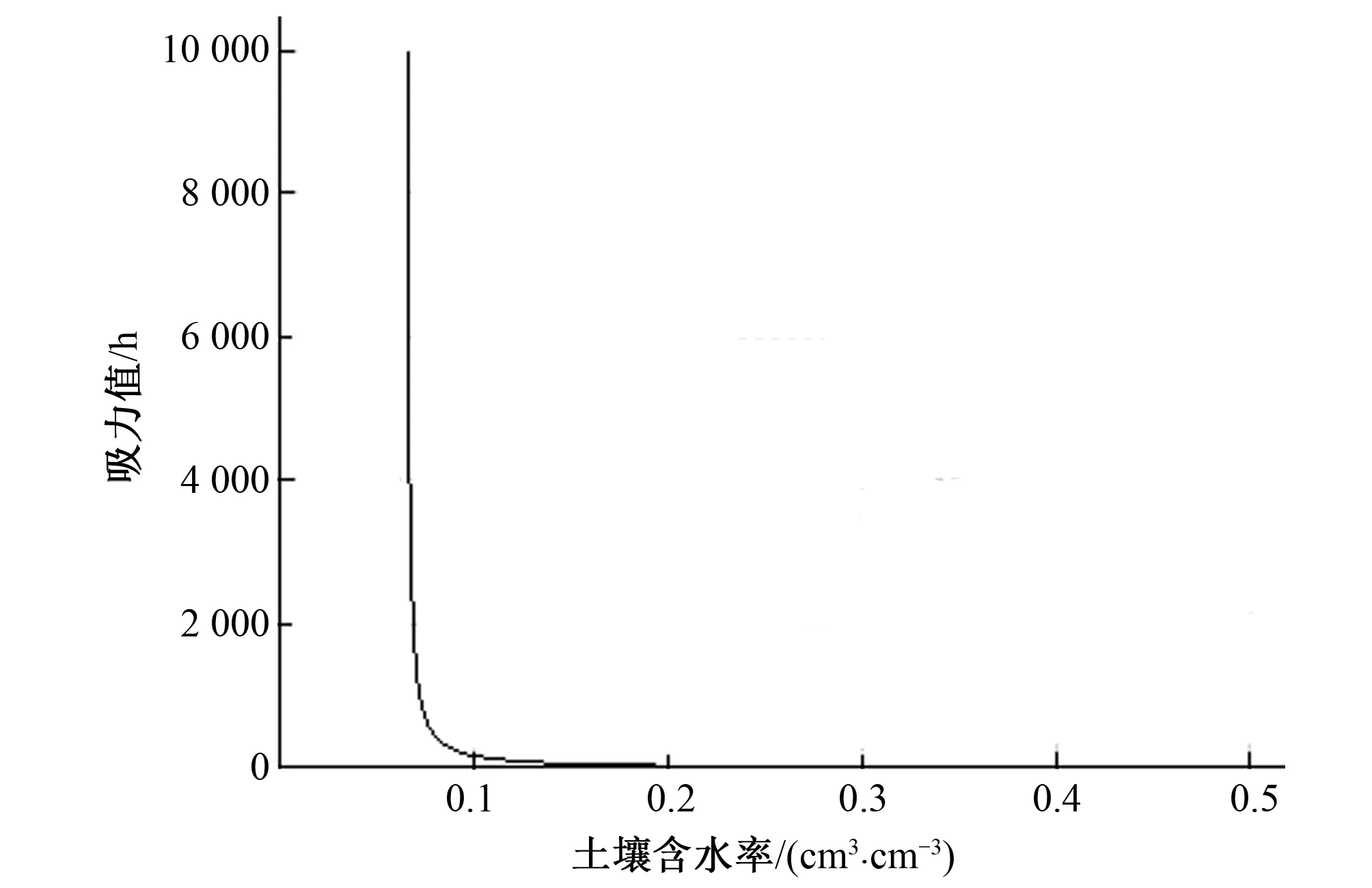
图5 土壤水分特征曲线

从图4可以看出，导水率K是随着土壤含水率的增加而增加，并且呈现出指数函数的增长趋势，当土壤含水率为30%时，所对应的导水率为0.2 cm/h，当土壤含水率增加至40%时，其土壤导水率可以达到2.4 cm/h，说明在土壤含水率比较大时，土壤水分的有效性增加，作物在土壤中能以较小的蒸腾拉力或者根压就能在土壤中获取生命需水量，对土壤含水率和导水率曲线进行拟合，发现其能较好地满足指数函数关系，具体如下式所示。

y=0.000 9 e19.356 x，R2=0.896 2

(10)

式中：y为土壤导水率，cm/h；x为土壤含水率，cm3/cm3。

对土壤水分特征曲线进行模拟，结果如图5所示，可以看出随着土壤含水率增大，吸力值减小，说明土壤含水率越大，其土壤对水分的保持能力减小，当土壤达到饱和含水率时，吸力值减小为0，利用V-G模型对模拟得到的土壤水分特征曲线进行拟合，拟合得到的结果如表3所示，其模拟得到的结果和前述实测得到的基本接近。

表3 土壤水分特征曲线V-G模型拟合结果

4 结 语

室内有机玻璃箱对滴灌土壤水分运移及其再分布试验，并用Hydrus软件进行了模拟，发现滴灌条件下土壤中水分分布是一个以滴头为中心逐渐向外扩散的过程，土壤含水率在水平方向所表现出中心对称的规律，并利用Hydrus软件对其土壤含水率分布及土壤力特性参数等进行了模拟，结果表明Hydrus软件对滴灌条件下的土壤水分分布的模拟具有一定的精度，特别是距离滴头较近的位置，用均方根误差RMSE和决定系数R2对模拟结果进行评价，发现在滴头处实测的土壤含水率和模拟的土壤含水率其RMSE和R2可以达到0.021 6和0.856 2，在距离滴头较远的位置其精度略低，但是基本可满足对土壤水分有效性和分析土壤水分运动的计算。通过Hydrus软件土壤水力特性功能进行模拟，得到了土壤水分特征曲线和扩散率曲线，并利用指数函数关系和V-G模型进行了拟合，对各参数进行率定，发现具有较高的决定系数，说明Hydrus软件对滴灌土壤水分运移的模拟具有较高的精度，利用该软件可在分析评价土壤水分的有效性，研究土壤水分运动等方面。