基于DRASTIC模型的地下水脆弱性评价综合赋权研究

胡旭东 ，聂晶晶 ，梅红波 ，李远远，任晓杰，李梦迪

(1.中国地质大学(武汉)资源学院,武汉 430074; 2.云南省环境监测中心站，昆明 650034)

地下水脆弱性一词最早是在1968年由法国的Albinet和Margat首次提出[1]，目前国际上比较公认的定义是1993年美国国家科学研究委员会给定的“地下水脆弱性是污染物到达最上层含水层之上某特定位置的倾向性与可能性”[2]。国内对地下水脆弱性的研究始于20世纪90年代中期[3]，虽然起步较晚，但是近十几年发展较快。地下水资源对于人们生活和社会发展起着不可替代的作用，已经越来越成为人们的关注的焦点。

地下水脆弱性评价方法主要有三类：迭置指数法、过程数学模拟法和统计方法[4]。三类方法各有优缺点，其中迭置指数法以其低成本、操作简单、数据易获取、表达直观等优点得到广泛的运用。迭置指数法中最常用也是最经典的评价模型是美国环保局在1987年提出的DRASTIC法[5,6]。该方法选取了7种与地下水脆弱性相关的指标，根据指标自身的属性建立评分系统，然后按照不同指标对脆弱性影响程度的大小对其分配权重，将评价区划分为若干个单元，对各单元的各评价指标进行加权求和，即得到脆弱性评价值，如公式(1)所示。

(1)

式中：Rij表示第i个评价单元第j个指标的评分；ωj表示第j个指标相应的权重。

DRASTIC模型的评价指标在传统权重分配方法上是综合了美国多位水文地质学专家的经验给出的。而在实际运用中，照搬这一套评权重值显然不合理，因为各个评价区的地理、地质以及水文地质条件都不尽相同，需要根据评价区的具体情况，结合对评价区属性的了解，合理选择评价指标以及判断出各个指标的相对重要程度。指标权重赋值直接决定评价结果的精度。地下水脆弱性研究中赋权方法主要包括主观赋权法和客观赋权法。主观赋权法对经验具有较强的依赖性，权值大小取决于分析者对实际情况的了解程度，决策结果具有较强的主观随意性，客观性较差；客观赋权法具有较强的数学理论依据，克服了主观意愿，然而赋权结果依赖于数据质量和数量，往往导致评价结果与实际情况不符，比如最重要的评价指标并未赋予最大的权重值。综合来看，主观方法和客观方法各利弊，而基于DRASTIC模型的地下水脆弱性评价对评价指标的赋权过程具有主观特点和客观特点[7]，因此本文结合两者进行综合赋权，其中主观方法选取的是改进的层次分析法(Analytic Hierarchy Process，AHP)，客观方法选取的是因子分析法(Factor Analysis，FA)。将层次分析法与因子分析法综合运用于地下水脆弱性评价之中，旨在确定相对合理的指标权重，最终提高评价结果的可信度。

1 DRASTIC评价指标的综合权重分配方法

1.1 主观赋权的层次分析法

层次分析法是1973年美国运筹学家Saaty创建的一种非常重要的决策方法[8]。作为主观赋权法[9]，层次分析法通过主观驱动，使用数学转换将性质明确但难以量化的问题定量化表达，具有操作简单、实用性和适应性强等优点[10,11]。层次分析法计算过程包括建立层次结构模型、构建判断矩阵、计算各指标的权重、一致性检验等步骤，其中首要的步骤是构建判断矩阵。传统的层次分析法以九尺度原则确定判断矩阵，然而指标间对应的重要程度不好把握，难以确定合理的判断矩阵。本文采用三标度法简化模型[12,13]，有利于比较相对关系，经过数学运算可由标度矩阵间接得到判断矩阵。此外，判断矩阵的一致性检验也是层次分析法中的核心问题，一致性检验通过加入平均随机一致性指标的检验系数CR衡量[14]，CR小于0.1即通过一致性检验。反之若CR大于0.1，表示偏离了一致性，则此时求得的权重矩阵W不可靠。

然而三标度法并未逃离层次分析法固有的缺陷，即一致性检验需要多次调试，调试过程中比较盲目，并不能确切地掌握是哪些因素导致的不一致结果，若一直不能通过一致性检验则要耗费大量的工作量[15]。因此本文在三标度的基础上引入最优传递矩阵的方法[16]，采用自调节方式将构建的标度矩阵转化为一致性矩阵，从而计算各个指标的权重值而不需要再进行一致性检验。具体计算过程如下：

利用三标度判断指标间重要程度关系，构建标度矩阵A=(aij)n×n，矩阵A满足aij=-aji，为反对称矩阵。三标度准则如表1所示。

表1 三标度判断值Tab.1 Standard based on 3 scale

设矩阵T=(tij)n×n为矩阵A的最优传递矩阵，其中：

(2)

若矩阵F中的元素满足fij=1/fji(互反矩阵)且fij=fik/fjk，即为一致性矩阵，利用传递矩阵确定一致性矩阵F=(fij)n×n，其中：

fij=exp(tij)

(3)

根据一致性判断矩阵F计算出各指标权重。F矩阵的最大特征值对应的特征向量作为各个指标的相对权重向量，即FX=λmaxX。其中，X=[X1,X2,…,Xn]T为特征向量，其近似值作为评价指标的相对权重。本文采用根法计算特征向量的近似值：

(4)

归一化得各个指标权重：

(5)

1.2 客观赋权的因子分析法

客观方法选用因子分析法，因子分析法是一种将高维数据降维的方法[17]。在地下水脆弱性评价中，一种被称为主成分-因子分析的方法被广泛运用于评价指标赋权方面[18,19]，其本质上还是因子分析法，只不过在因子荷载矩阵的计算上使用了主成分法。除了主成分法，还有主轴因子法、最小二乘法、极大似然法等方法可以计算出因子荷载矩阵[20]。

因子分析法是在主成分分析法基础上发展而来的，其基本思想是，在保证原始信息量丢失最少的情况下，使用降维方法，分析原始变量之间的公共关系，将原始变量进行归类，归类后的因子称为公共因子，使得原本需要许多信息重叠的变量描述的问题，通过因子分析法后变成少数几个带有主要信息的公共因子即可描述。

因子分析法的步骤是：对原始变量进行标准化，计算样本相关系数矩阵R、求解R的特征根λi(λ1≥λ2≥…≥λp>0)和相应的标准正交的特征向量li，确定公共因子数m(按前m个特征值之和占特征值总和的百分比来确定)，计算主因子载荷矩阵A=[aij]；根据需要对载荷矩阵进行旋转，得到能被更好解释的公共因子，最后计算因子得分矩阵。整个计算过程可以通过软件SPSS快速实现。因子分析的主要目的是计算可解释的公共因子、各个样品在公共因子上的得分及各变量的权重。由得分矩阵可得出各主因子的得分，如公式(6)所示。

(6)

式中：fi为第i个主因子的得分；βij为相应的得分系数。

由于主因子可以代替原来的变量研究问题，而每个主因子fi对事件的贡献度可以用相关系数矩阵的特征根λi衡量，则原始变量的权重值是由每个主因子的特征值做权数对每个主因子得分系数进行加权求和得到，如公式(7)所示。

(7)

由公式(6)和(7)可以计算各变量的权重，如公式(8)所示。

(8)

归一化后得最终的权重值，如公式(9)所示。

(9)

需要指出的是，由主成分分析求出的因子荷载矩阵只是一个很基础的矩阵，理论上因子荷载矩阵有很多种，一般求解过程会进行因子旋转，目的是使因子荷载值两极分化，趋向于0或者±1，相关系数矩阵的特征值则会发生变化，即方差贡献度会变化，但是主因子的总贡献度保持不变。之后由因子荷载矩阵求得的因子得分系数以及后续得到的权重值发生改变。上述内容表明理论上得出的权重值不唯一，介于因子旋转之后更符合实际意义和解释，本文在求解权重时使用因子旋转之后的结果。

1.3 综合赋权

综合赋权结合了主观赋权和客观赋权，综合两者信息，既尊重主观又不失客观[21]。计算方法一般包括积法以及和法。和法的公式添加了一个人为估计的参数，用来衡量主观权值和客观权值的重要程度，导致该方法操作较为复杂，而且对于参数尺度也不好把握，因此本文选择积法求取综合赋权值，如公式(10)所示[22]。

(10)

2 实例应用

2.1 研究区概况

昆明安宁工业园草铺片区位于云南省安宁市草铺镇中部，占地面积约为62 km2。研究区属中亚热带低纬度高海拔地区，平均海拔1 800 m，年平均气温14.8 ℃，年平均降雨量1 087.2 mm。区内地表水系发育，主要为鸣矣河和螳螂川，鸣矣河是螳螂川的一级支流，在连然镇通仙桥汇入螳螂川。地下水类型主要包括碎屑岩裂隙水、火成岩裂隙水以及孔隙水，富水性为中等。区内地下水主要接受大气降水补给，局部受地表水补给，多以分散的隙流或片状散流形式向当地最低排泄基准面螳螂川干、支流排泄。

经过近15年的发展，草铺片区已成为云南省主要石油及磷化工基地，由于工业的快速发展，以氟化物、烟(粉)尘以及二氧化硫等为主的企业污染物对当地大气环境、土壤环境、植物农作物等造成不同程度的影响[23]。研究区基本处于地下水的排泄区，且大部分区域浅层地下水埋深较浅，为易受污染区。当地地下水资源正受到严重的潜在威胁。

2.2 研究区地下水脆弱性评价

(1)评价指标选取。本文基于DRASTIC模型，结合研究区地质、地理、水文等条件选取适合的指标。考虑到评价区的实际情况以及指标数据的可获得性，选取地下水埋深、河网密度、降雨量、地形坡度、含水层厚度、包气带介质以及含水层渗透系数等7个指标来描述评价区地下水脆弱性。传统的DRASTIC模型指标还应包括含土壤类型，研究区内土壤类型与包气带介质分布比较一致，该指标对研究区地下水脆弱性评价并无太大意义，故舍弃。区内水系发达，河网密集分布，河网切割侵蚀易影响包气带介质，进而影响地下水脆弱性[24]，故选用河网密度代替土壤介质。各个指标评分如表2所示。

表2 指标等级划分以及评分Tab.2 Ranges and ratings for indexes

(2)权重计算。根据评价区水文地质条件特点，结合专家意见，确定该研究区指标对地下水脆弱性影响程度关系为：地下水埋深>降雨量=包气带介质>含水层厚度>含水层渗透系数>河网密度=地形坡度。依据三标度原则确定标度矩阵(表3)，构造传递矩阵进而间接求出层次分析法的一致性判断矩阵(表4)，计算出的AHP权重值如表7所示。本次脆弱性评价借助GIS平台[25]，将评价区划分为24 801个单元(单元大小为50 m×50 m)，把每个单元内包含的7种指标属性导入到SPSS软件，包气带介质为定性数据，没有具体的数值即选用评分值代替，算得的因子旋转后的特征值与方差贡献度如表5所示，选择特征值大于1且累加贡献度大于80%的为前3个主因子，得分系数矩阵如表6所示，则由因子分析法得到的权重如表7所示。将两种权重值带入公式(10)，得到最终的权重值(表7)。

表3 标度矩阵Tab.3 Scale matrix

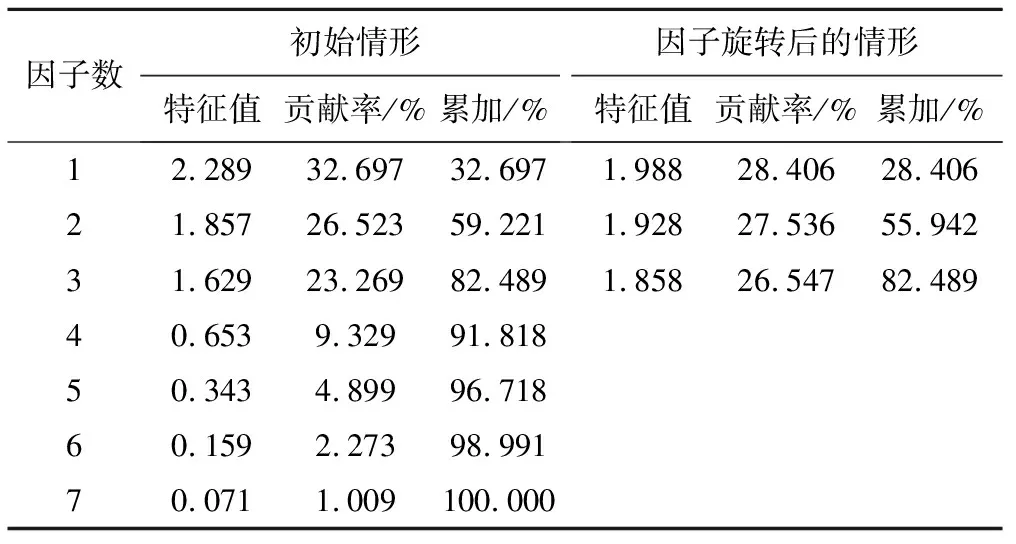
表5 特征值与方差贡献度Tab.5 Eigenvalues and variance contribution rate

表6 得分系数矩阵Tab.6 Factor score matrix

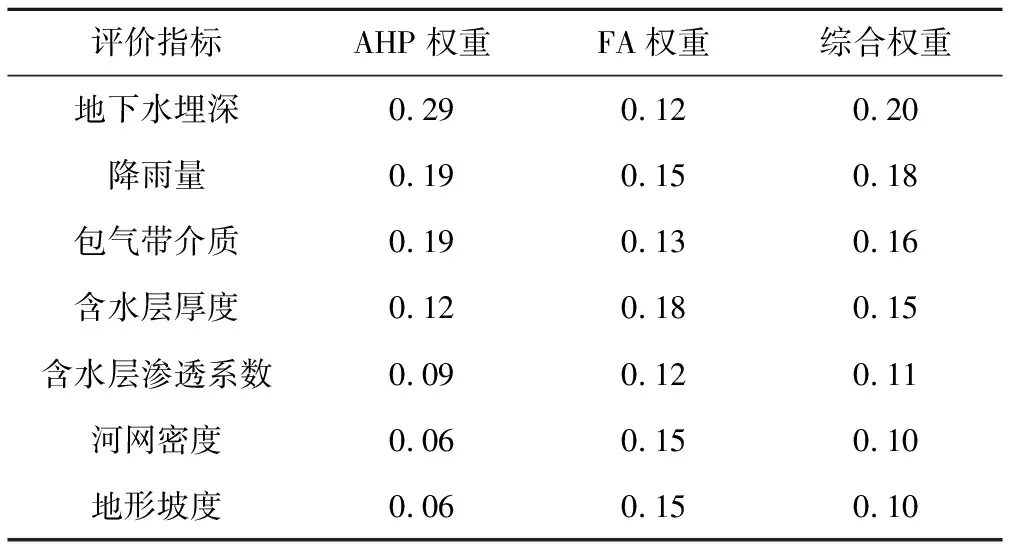
表7 评价指标权重分配统计表Tab.7 The table of index weight distribution

(3)地下水脆弱性评价。利用得到的综合权重值，按照公式(1)将各个指标的评分进行加权求和，得到研究区地下水脆弱性评价值。理论上脆弱性评价值范围为1～10，按照等间距分为5个级别，即低级别、较低级别、中等级别、较高级别、高级别，评价结果如图1所示。级别为低的区域占研究区面积的18.45%，主要分布在研究区东侧；级别为较低的区域分布最多，占研究区的50.64%；中等级别的区域分布也较多，约占28.29%，主要位于研究区中部以及少量分布在西侧；较高级别的区域分布较少，约占1.71%，主要在研究区中心地带，此区域地下水埋深浅且含水层厚度小；高级别的区域分布最少，约占0.91%。研究区地下水脆弱性整体情况比较良好。此外，为验证综合权重法的合理性，本文分别使用层次分析法以及因子分析法得到各指标的权重值并计算出研究区地下水脆弱性分级进行比较(图2)。

图1 研究区地下水脆弱性评价结果图(综合赋权)Fig.1 Groundwater vulnerability assessment of study area(combination)

图2 研究区地下水脆弱性评价结果图Fig.2 Groundwater vulnerability assessment of study area

(4)评价结果验证与对比。采用单点特征污染物浓度和该点地下水脆弱性指数之间联系的强弱的斯皮尔曼相关系数ρ进行评价结果验证[26]，如公式(11)所示。

(11)

式中：ui和vi分别为两变量按等级大小或优劣排序后的秩；n为样本数量；ρ为斯皮尔曼相关系数。

评价区共布置了14个地下水监测点(图1)，监测点信息见表8。云南省环境监测中心站在2017年4月25日-4月26日进行了地下水采样，采集了pH、氯化物、硫化盐、硝酸盐氮、亚硝酸盐、氨氮、石油类、挥发酚、铅等污染物数据信息。氨氮浓度是衡量水体受污染程度的重要指标之一[27]，选取氨氮为特征污染物，参照《地下水质量标准》(GBT-14848-2017)中的规定分级，结合脆弱性评价结果，得到各监测点氨氮含量等级及脆弱性等级分类对照表(表9)。根据公式(11)分别算出3种赋权方法的斯皮尔曼相关系数，结果显示综合权重法的相关系数最高，在95%的置信度下为0.604；因子分析法的相关系数次之，为0.373；而层次分析法最低，仅为0.308。上述结果表明相比主观权重法以及客观权重法而言，综合权重法的评价结果精度得到提高。并且经过综合权重法后研究区脆弱性评价等级与氨氮含量呈中度相关性，评价结果具有可靠性。

表8 研究区地下水监测点氨氮数据信息Tab.8 Information of surveillance site in study area

3 结 语

本文基于DRASTIC模型就脆弱性评价中评价指标的权重问题展开讨论。指标权重大小反映该指标对地下水脆弱性的影响程度，其分配结果直接影响评价结果的合理性，赋权过程需要考虑主观判断和客观信息，分别采用层次分析法和因子分析法进行赋权，并结合两者得出最终的权重值。通过在云南省安宁市工业园草铺片区的实例应用，验证了综合赋权方法的可靠性。本文主要结论如下：

(1)传统层次分析法不便于使用，故引入三标度准则以及传递矩阵，有利于判断指标间重要程度关系和简化一致性检验，推广了层次分析法的使用。

表9 各监测点氨氮含量等级及脆弱性等级分类表Tab.9 Ratings for ammonia nitrogen and groundwater vulnerability at surveillance site

(2)综合赋权结果显示，地下水埋深和降雨量占有较大比重，而河网密度和地形坡度比重较小，符合研究区实际情况。主观赋权结果与客观赋权结果差异最大的3个指标分别是地下水埋深、河网密度以及地形坡度。根据主观判断，地下水埋深应具有最大的权重值而河网密度和地形坡度的权值应最小；然而客观赋权结果显示地下水埋深对脆弱性的影响并不大，反而河网密度以及地形坡度的作用得到大幅增长。就脆弱性评价结果而言，主观赋权的结果略显平缓，基本处于较低级别，而客观赋权的结果显示研究区地下水脆弱性基本处于较高级别，造成这一现象可能是由于两种赋权方法给予河网密度以及地形坡度的权重差异造成的。客观赋权法中脆弱性评价级别较高的区域里，河网密度值以及坡度值都比较大，加上较高权重的影响因此最终的评价值较高，反观主观赋权由于权值的稀释而造成这些区域的评价值不高。

(3)以云南省安宁市工业园草铺片区地下水脆弱性评价为例，经过斯皮尔曼系数的验证，综合权重法的相关系数最高，氨氮含量等级与脆弱性等级呈现中度相关性。相比之下，主观赋权及客观赋权下的氨氮含量等级与脆弱性等级仅为弱相关，表明在地下水脆弱性研究中综合权重法具有一定的合理性，有必要结合主观判断以及客观信息综合考虑。而主观赋权的相关系数最低，可见决策时决不能仅凭主观臆断，应充分尊重事物的客观性。

安宁市工业园草铺片区地下水整体情况比较良好，基本处于中等级别及以下，然而情况也不容乐观。排污量较大的石油炼化产业和磷盐化工产业基本位于中等级别区域，这些区域地下水埋深较浅，包气带介质吸附净化能力较差，地下水资源受污染的潜在可能性仍然较大，相关政府部门及企业应做好防护处理，尽量避免在工业正常生产条件下，发生废料下渗污染地下水的情况。