基于冗余联动的六轴联动数控机床加工轨迹误差优化
2019-03-06张鹏翔李学崑
张鹏翔 周 凯 李学崑
(清华大学机械工程系, 北京 100084)
0 引言
六轴联动数控机床是一种具有3个平动联动轴和3个旋转联动轴的多轴联动数控机床。与五轴联动数控机床相比,该类机床增加了一个旋转联动轴。因此,六轴联动主要应用于刀具不绕自身轴线旋转的加工设备,如电火花加工机床和焊接加工设备[1-2];或者用于齿轮加工等制造设备[3-8]。在刀具旋转时,六轴联动的特点是所增加的旋转联动轴可认为是冗余联动或者冗余自由度。该特点能保证设备满足运动关系的前提下,实现额外的约束功能[9-11]。
加工轨迹误差主要由于刀具相对于工件的实际运动与理论运动不一致所产生。迄今,针对该误差的优化研究,均需结合机床运动学模型,如在数控系统中,根据该模型对联动轴的运动量进行实时修正[12],该类方法能够根据联动轴的实际位置响应对加工轨迹误差进行在线修正。因此,误差优化效果最优,但必须在数控系统的实时算法层面实现。当机床采用第三方数控系统时,该类方法无法应用。或者,在计算联动轴的运动量时,根据模型优化刀具中心点运动轨迹误差[13-14],或者优化刀具轴线矢量转动误差[15-16],此类方法主要在刀具中心点运动轨迹中插入新的刀具中心点,或者在刀具轴线转动轨迹中插入新的刀具轴线矢量,从而实现加工轨迹误差的优化。该类方法可用于机床的后置处理,具有较好的通用性,但由于所插入的刀具中心点或新的轴线矢量无法考虑到刀具与工件之间的接触或方向关系,因此,该类方法并不能保证误差优化具有很好的效果。
本文以用于抛光加工的六轴联动数控机床为研究对象,通过建立其运动学模型,研究其冗余联动特点。建立加工轨迹误差与联动轴运动之间相互关联的数学模型,提出以冗余联动轴优化加工轨迹误差的方法。在该机床上应用所提出的加工轨迹优化算法进行对比实验,对实验中的加工轨迹误差和抛光后工件表面粗糙度进行分析,以验证本文所提出优化方法的有效性。
1 六轴联动机床运动学模型与冗余联动
机床运动学模型的主要作用为将刀具相对工件的运动映射成联动轴的运动,即将工件静止时,刀具相对于工件的运动轨迹转换成机床联动轴的运动轨迹。当工件静止时,刀具运动轨迹可以用刀具中心点p和刀具轴线矢量u描述,其中p和u分别表示为
(1)
式中px、py、pz——刀具中心点p在X、Y和Z方向上的分量
ux、uy、uz——刀具轴线矢量u在X、Y和Z方向上的分量
本文所研究的六轴联动数控机床应用于卫浴产品的抛光加工,刀具为抛光轮,其结构图如图1所示,具有X、Y和Z3个平动联动轴,A、B和C3个旋转联动轴,其中B、C轴位于工件处。在图1中,机床的B轴和C轴处于可360°旋转的转盘上,为了上下料方便,此时,B轴处于-90°,使得此时的C轴轴线和A轴轴线平行。为了描述该机床联动轴的运动,建立机床坐标系如图2所示,其中OmXmYmZm为机床坐标系,OwXwYwZw为工件回转坐标系,OtXtYtZt为抛光轮平动坐标系,抛光轮中心点p与Ot重合,OtlXtlYtlZtl为抛光轮摆动坐标系。为了研究方便,设机床坐标系与工件回转坐标系相重合,则rm为零矢量。机床的初始状态为各个联动轴的运动量为0时对应的状态。矢量rn为该状态下抛光轮摆动坐标系原点在抛光轮平动坐标系下的坐标,以齐次坐标表示为
rn=(nx,ny,nz,1)
式中nx、ny、nz——矢量rn在X、Y和Z方向上分量
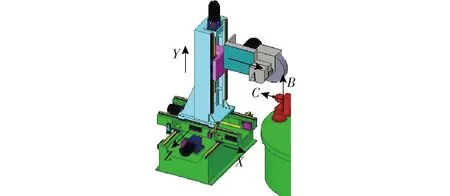
图1 六轴联动数控机床装配图Fig.1 Assembly drawing of six-axis linkage CNC machine tool

图2 六轴联动数控机床坐标系示意图Fig.2 Diagram of coordinate systems of six-axis linkage CNC machine tool
由图1和图2关于机床联动轴和坐标系的描述,能够建立联动轴运动与抛光轮中心点p和抛光轮轴线矢量u之间的数学模型。因此,本文研究的六轴联动数控机床运动学模型可表示为
[p1]T=R(-θC)R(-θB)T(s+rn)·
R(θA)T(-rn)[0 0 0 1]T
(2)
[u0]T=R(-θC)R(-θB)T(s+rn)·
R(θA)T(-rn)[0 0 1 0]T
(3)
其中
s=(sx,sy,sz,1)
式中θA——A轴转动角θB——B轴转动角
θC——C轴转动角sz——Z轴运动量
T——平移运动齐次坐标变换矩阵
R——旋转运动齐次坐标变换矩阵
sx——X轴运动量sy——Y轴运动量
将式(3)展开可得
(4)
由于抛光轮轴线矢量u为单位矢量,式(4)只有两个独立方程,同时具有3个未知数(3个旋转联动轴的运动量),因此,式(4)为冗余方程组。对于给定的抛光轮轴线矢量,式(4)的解,即A、B、C轴的运动量理论上有无穷多组。
如图1所示,由于机床的C轴通过夹具与工件直接连接,C轴的转动可以直接驱动工件转动,而不依赖于其他旋转联动轴,将C轴视为冗余联动轴,即C轴的运动量设为已知,则其余5个联动轴的运动量为
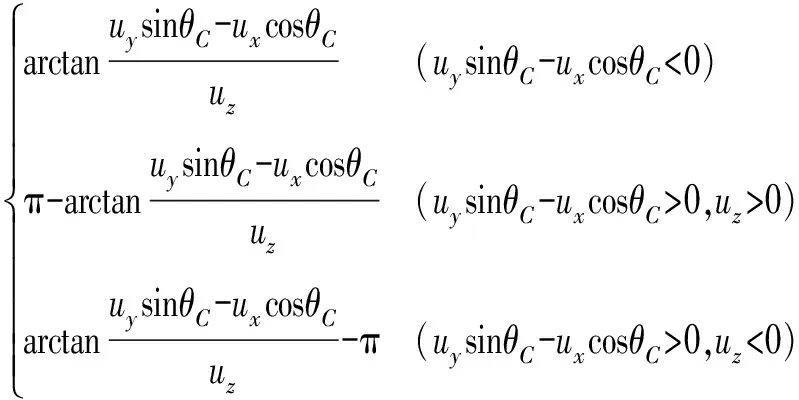
(5)
(6)
由式(5)、(6)可知,需先以附加约束条件确定C轴的运动量,进而计算出其他5个联动轴的运动量。因此,本文研究的六轴联动数控机床为冗余系统,联动轴的运动在满足抛光轮中心点位置和抛光轮轴线矢量方向的前提下,可以实现额外的附加功能。本文所研究的附加功能为加工轨迹误差的最小化。
2 加工轨迹误差
2.1 接触点轨迹
在本文研究的六轴联动数控机床中,加工轨迹为抛光轮与工件的相对运动轨迹,即抛光轮上与工件相接触的点在工件表面上的运动轨迹。当抛光轮相对于工件出现转动时,无法仅以其中心点的运动轨迹来准确描述加工轨迹,需同时考虑抛光轮相对于工件的转动。抛光轮与工件的接触关系如图3所示。
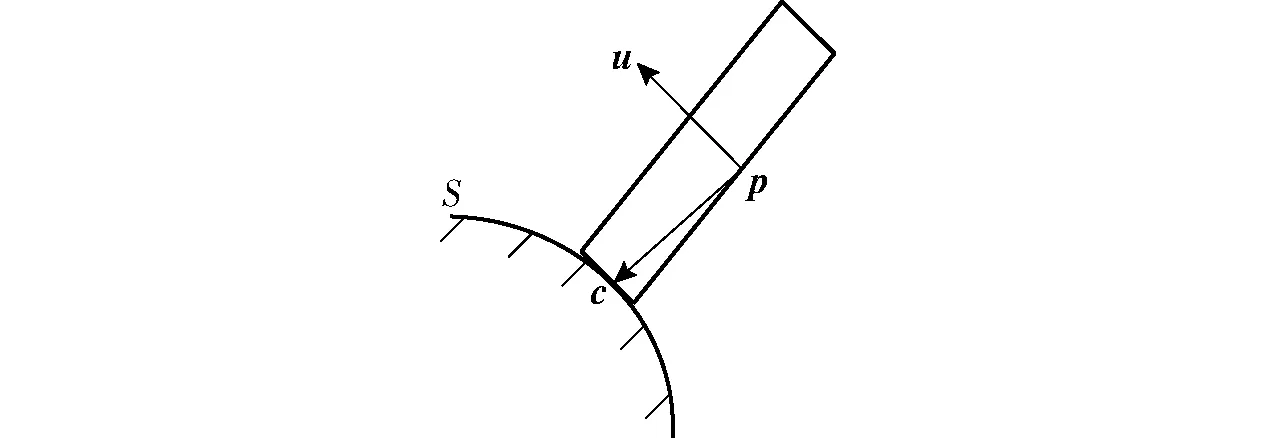
图3 抛光轮与工件接触点示意图Fig.3 Diagram of contact point between polish wheel and workpiece
在图3中,p为抛光轮中心点,u为抛光轮轴线矢量,c为抛光轮与工件的接触点,S为工件表面。为了研究方便,设抛光轮转速为0,加工轨迹可转换为抛光轮上与工件相接触点的运动轨迹,即点c的运动轨迹。
定义在某个加工轨迹段中,起始点处抛光轮中心点坐标为p1,抛光轮轴线矢量为u1,对应X、Y、Z、A、B和C轴的运动量为sx1、sy1、sz1、θA1、θB1、θC1;结束点处抛光轮中心点坐标为p2,抛光轮轴线矢量为u2,对应X、Y、Z、A、B和C轴的运动量为sx2、sy2、sz2、θA2、θB2、θC2。
由刚体运动规律可知,接触点c的运动可分解为:跟随抛光轮中心点p的平移和相对于该中心点的定点转动。则接触点c的运动轨迹可表示为
c=p+Ruax(θax)pc
(7)
式中pc——抛光轮中心点p至接触点c的矢量
θax——接触点绕抛光轮中心点的转动角
下标uax表示接触点c绕抛光轮中心点p的转动轴线。
转动轴线uax由抛光轮轴线确定,可表示为
uax=u1×u2
(8)
因此,接触点运动轨迹,即加工轨迹,由抛光轮中心点的平动轨迹和接触点绕该中心点的转动轨迹合成而得。
2.2 抛光轮中心点轨迹误差
在本文所研究的六轴联动数控机床中,抛光轮中心点的理论运动轨迹pr(t)可以用直线段拟合,表示为
pr(t)=
(tpx2+(1-t)px1,tpy2+(1-t)py1,tpz2+(1-t)pz1,1)
(9)
式中t——在[0,1]之间的无量纲自变量
px1、py1、pz1——p1在X、Y和Z方向上的分量
px2、py2、pz2——p2的X、Y和Z方向上的分量
数控系统一般采用线性插补控制联动轴的运动,因此机床各个联动轴的运动轨迹为
(10)
由于抛光轮相对于工件的运动是由机床联动轴的运动合成而得,因此抛光轮中心点实际运动轨迹p(t)为
[p(t) 1]T=R(-θC(t))R(-θB(t))T(s(t)+n)·
R(θA(t))T(-n)[0 0 0 1]T
(11)
由式(11)可知,抛光轮中心点的实际运动轨迹为曲线。结合式(10),抛光轮中心点的理论运动轨迹与实际运动轨迹的误差εp(t)为
εp(t)=|p(t)-pr(t)|
(12)
由抛光轮中心点平动误差所导致的接触点运动误差同样可由式(12)表示。
2.3 抛光轮轴线转动轨迹误差
为了研究方便,设抛光轮中心点静止,则此时接触点的运动由抛光轮轴线转动引起。一般而言,在设计抛光轮运动轨迹时,希望抛光轮轴线在u1处以恒定角速度转动至u2处,该转动轨迹ur(t)可表示为
ur(t)=ξ1(t)u1+ξ2(t)u2
(13)
式中ξ1(t)、ξ2(t)——与u1、u2和t有关的函数
因此,抛光轮轴线的理论转动轨迹,即ur(t)的转动轨迹为在u1和u2所组成的平面内,从u1至u2且半径为1的圆弧,圆心为中心点p,重新表示为
(14)
式中θ——轴线矢量u1和u2的夹角
由机床运动模型式(3)和联动轴运动轨迹关系式(10)可知,抛光轮轴线的实际转动同样由旋转联动轴的运动合成而来,即为
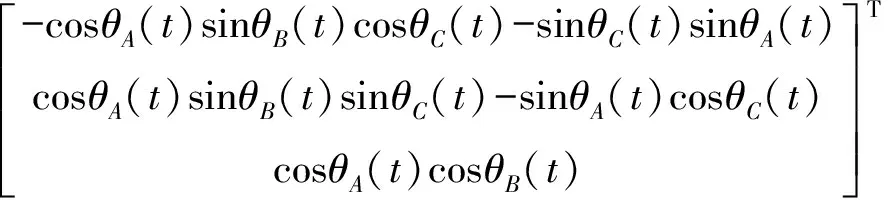
(15)
由式(15)可知,抛光轮轴线的实际转动轨迹为在半径为1的球面上的曲线,且起始点为u1,结束点为u2,球心为中心点p。
可知抛光轮轴线的理论转动轨迹和实际转动轨迹两者之间存在夹角误差θr(t),可表示为
θr(t)=arccos(u(t)ur(t))
(16)
因此,由于抛光轮轴线转动夹角误差导致的接触点运动误差εu(t)为
(17)
由式(17)可知,当轴线夹角误差越大,所引起的接触点运动轨迹误差也越大。
2.4 接触点轨迹误差
由2.2节和2.3节可知,由于接触点相对于抛光轮中心点的平动和转动相互正交,接触点运动的平动误差和转动误差也相互正交。结合式(12)、(17),接触点实际运动轨迹误差ε(t)为
(18)
由于本文所研究的六轴联动数控机床具有冗余联动特点,由式(5)、(6)可知,接触点轨迹误差同时与冗余旋转联动轴C轴的运动量有关,则其可表示为
(19)
3 加工轨迹误差优化
由第2节可知,加工轨迹误差,即接触点运动轨迹误差,是由抛光轮中心点平动轨迹误差和抛光轮轴线转动轨迹误差所引起的。因此,需要对这两个误差进行优化,从而实现接触点轨迹误差的优化。
由式(19)可知,本文所研究的六轴联动数控机床具有冗余联动特点,通过冗余旋转联动轴C轴的运动,可以实现抛光轮中心点平动误差和抛光轮轴线转动误差的最优,从而达到加工轨迹误差的优化。
3.1 抛光轮中心点运动轨迹误差优化
为了研究抛光轮中心点平动轨迹误差εp(t)的优化,根据式(12),将该误差在X、Y和Z方向上分解,可表示为
(20)
式中εpx(t)、εpy(t)、εpz(t)——误差εp(t)在X、Y、Z方向上的分量
将式(20)中的三角函数在t为0处以泰勒级数展开,可表示为
(21)
因此,在该段抛光轮中心点轨迹段内,当A、B、C3个旋转轴的变化量越小,结合式(21),则机床X、Y、Z联动轴运动量越接近中心点的理想运动轨迹在对应方向上的分量,即为
(22)
进一步根据机床运动学模型式(2),可以得到A、B、C3个旋转轴的变化量与抛光轮中心点轨迹误差的X、Y、Z方向分量之间的关系为
(23)
由式(23)可知,在该段轨迹内,当A、B、C轴的运动量越小时,抛光轮中心点运动轨迹误差也越小,即有如下关系
(24)
由于A、B、C3个旋转联动轴相互正交,因此式(24)可转换为

(25)
式(25)表明,当C轴的转动使得A、B轴及自身的运动量最小,可使得抛光轮中心点轨迹误差最小。
3.2 抛光轮轴线转动轨迹误差优化
如式(17)所示,当实际轴线矢量与理论轴线矢量之间的夹角误差越小,由此引起的接触点轨迹误差也越小。因此,可以通过C轴的转动,使得式(16)中的夹角误差最小,从而优化其引起的接触点轨迹误差。根据本文机床的冗余联动特点,两个轴线矢量的夹角误差大小同时与C轴的运动有关,由式(17)可以定义二元函数
(26)
式中g(θC(t),t)——抛光轮实际轴线与理论轴线的点积
由于式(26)在t为0和1时取值为0,因此存在t0符合如下关系
(27)
结合式(16)可知,在θC固定时,夹角误差在t0时为最大值。此时,抛光轮轴线矢量实际值为

(28)
由于式(28)在式(27)的条件下,只有θC(t0)为变量。因此,有如下条件
(29)
式(29)中,由于3个旋转联动轴的运动量只和初始和结束状态有关,可重新表示为
(30)
结合式(17),当3个旋转联动轴的运动量均为最小时,由抛光轮轴线转动误差所导致的接触点运动误差为最小,即为

(31)
式(31)表明,当C轴的转角使得A、B轴及自身的运动量最小时,可使得抛光轮轴线转动轨迹误差及其导致的接触点运动轨迹误差最小。
3.3 接触点轨迹误差优化
由3.1、3.2节研究结果可知,关于抛光轮中心点运动轨迹误差和抛光轮轴线矢量转动误差的优化条件完全相同,因此,该优化条件可以优化接触点运动轨迹误差,则该条件下对应的C轴运动可表示为
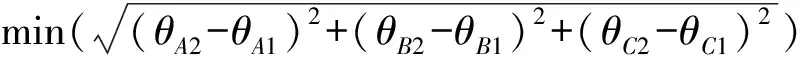
(32)
式中f(θC2)——C轴优化接触点轨迹误差的函数
式(32)中,起始点处3个旋转联动轴的运动量为已知,即θA1、θB1和θC1已知。因此,在该式中,结束点处C轴的转角使得在对应加工轨迹段内A、B、C轴的变化量最小,可以使得接触点的运动轨迹误差最小,即加工轨迹误差为最小。
式(32)的边界条件为该式所得到的各联动轴运动量需处于表1的行程范围之内,否则无法进行实际加工。如联动轴运动量出现超程,则重新计算,取符合所有联动轴行程限制且式(32)最小的一组联动轴运动量。本文所研究的机床各联动轴的实际行程如表1所示,同时rn为(0,80 mm,0,1)。

表1 机床联动轴行程Tab.1 Strokes of linkage axes of machine tool
由表1可知,C轴没有行程限制,即能实现-180°~180°的旋转,如果θC2直接在该区间内取值计算,则计算比较繁琐。因此,引入一种寻优算法以减小计算量。当一个加工轨迹段内,抛光轮轴线u1和u2平行时,由机床运动学模型式(2)、(3)可知,3个旋转联动轴均保持静止,机床以XYZ3轴联动进行加工,此时加工轨迹误差为0。由于C轴的转动可以改变u1和u2之间的夹角,可使得两者之间的夹角最小,即存在θC2p,有如下条件成立
max(Rot(θC2p)u2u1)
(33)
由式(33)可以进一步计算θC2p,可表示为
θC2p=90°-φ
(34)
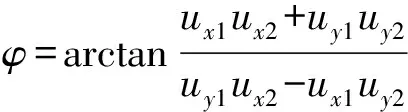
(35)
式中φ——与u1和u2有关的角,取为-90°~90°
由于式(33)的C轴转动无法改变抛光轮轴线矢量在Z方向上的分量,该情况下加工轨迹误差大于式(32)所对应的误差。因此,接触点轨迹误差最小对应的C轴角θCop区间表示为
θCop∈[θC1-|θC2p|,θC1+|θC2p|]
(36)
在实际计算中,可在式(36)对应的区间中,C轴以数控系统旋转轴分辨率0.001°为变化量,寻找满足表1前提下,符合式(32)的6个联动轴运动量,从而减小该优化方法的计算量。
4 抛光加工实验
为了验证所提出的加工轨迹误差优化算法有效性,在六轴联动数控机床(图1)上进行加工实验。抛光加工主要是为了降低工件表面粗糙度,抛光轮与工件为半刚性或者柔性接触,即抛光轮的变形产生与工件之间的接触压力。因此,当加工轨迹出现误差时,接触压力同时也出现误差[17-18]。由于在其他条件(如加工轨迹等)不变时,工件表面的抛光去除率由接触压力决定。当加工轨迹误差使得接触压力出现变化时,导致出现欠抛现象,从而影响工件抛光后的表面粗糙度和粗糙度均匀一致性[19-20]。因此,可以用工件抛光后的表面粗糙度和均匀一致性衡量加工轨迹误差。测试工件如图4所示。
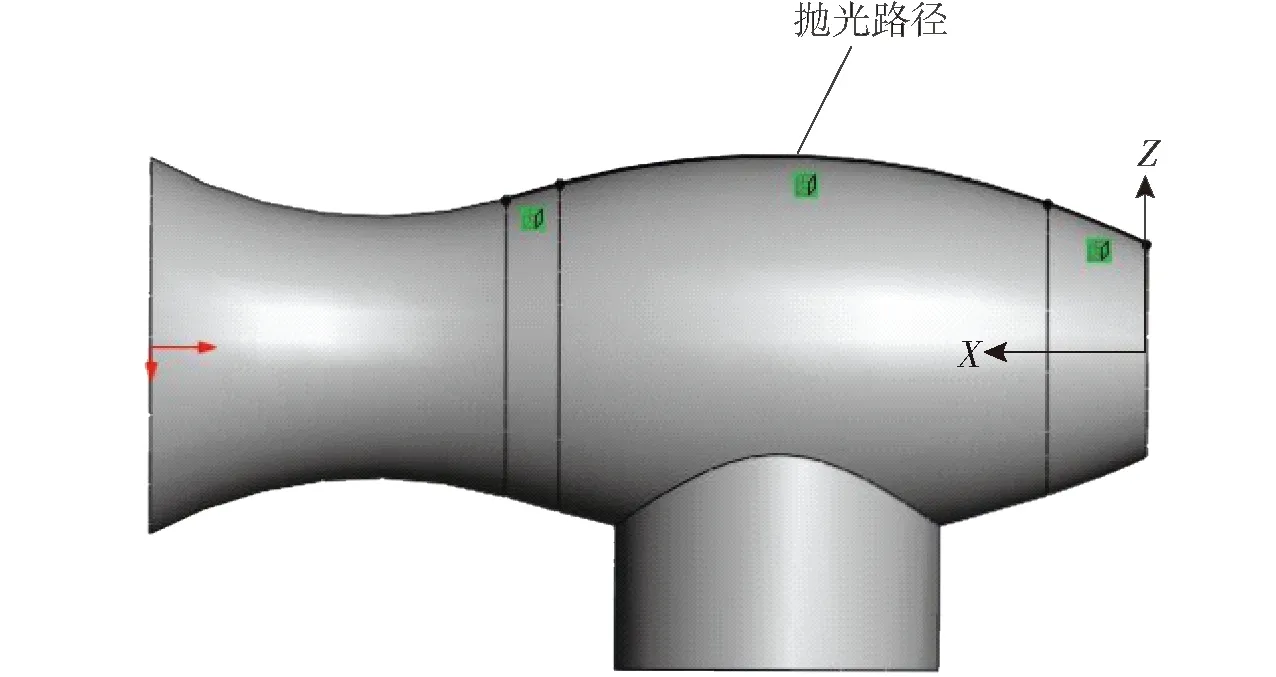
图4 加工工件示意图Fig.4 Diagram of processing workpiece
如图4所示,在初始状态时,工件的X轴与机床的X轴平行,Z轴与机床的Z轴平行。由于工件的表面由曲面组成,且在加工时为了保证抛光轮轴线与抛光路径的切线相平行,机床需要五轴联动才能实现加工。为了比较加工轨迹误差,实验采用了XYZAB五轴联动和XYZABC六轴联动分别对工件进行加工,且抛光路径完全相同,抛光轮转速均为1 000 r/min,抛光轮中心点沿工件表面的运动速率均为3 000 mm/min,抛光轮直径为300 mm,厚度为25 mm。因此,这2种联动情况下,抛光质量的差别源于加工轨迹误差。其中,在五轴联动时,C轴保持静止,且转角为0°;在六轴联动时,C轴的运动量由式(32)和表1确定。
为了验证优化算法的可行性,选取工件的其中一段加工轨迹进行详细计算和仿真说明。该轨迹的起始点处抛光轮中心点坐标为(-6.226 853 292 mm, 14.675 038 069 mm, 25.876 051 55 mm),抛光轮轴线单位矢量为(0.944 281 36, 0.324 139 00, 0.057 154 45);结束点处抛光轮中心点坐标(4.005 985 873 mm, 17.138 363 010 mm, 30.219 558 04 mm),抛光轮轴线单位矢量为(0.999 327 03, 0.036 123 61, 0.006 369 57)。
在XYZAB五轴联动情况下,起始点处各个联动轴的运动量为:(-26.205 mm,10.356 mm,-30.583 mm,-18.913°,-86.536°,0°)。
结束点处各个联动轴运动量为:(-30.193 mm,17.086 mm,1.309 mm,-2.070°,-89.635°,0°)。
在六轴联动情况下,C轴的运动由式(33)确定,起始点处各个联动轴运动量为:(-26.205 mm,10.356 mm,-30.583 mm,-18.913°,-86.536°,0°)。
结束点处各个联动轴运动量为:(-30.210 mm,16.202 mm,-12.923 mm,-10.494°,-89.630°,8.424°)。
此时,式(34)对应的θC2p为16.875°,式(32)得到的θC2属于式(36)对应的区间之内,符合实际情况,同时式(32)的计算量得到简化。
由各个联动轴在上述两种不同联动方式的运动量可知,结合式(33),五轴联动下AB轴的变化量之和大于六轴联动下ABC轴的变化量之和。由表1可知,两种联动方式下各联动轴的运动量均处于对应的行程之内,即均可以实现加工。
根据式(2)、(3),由Matlab软件分别绘制出在五轴联动和六轴联动情况下,该段加工轨迹下的抛光轮中心点实际运动轨迹和抛光轮轴线矢量实际转动轨迹,分别如图5、6所示。
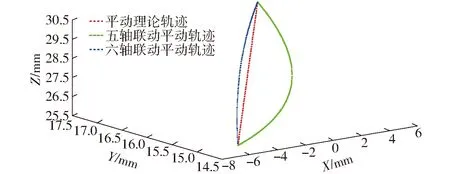
图5 抛光轮中心点运动轨迹Fig.5 Trajectory of polish wheel center point
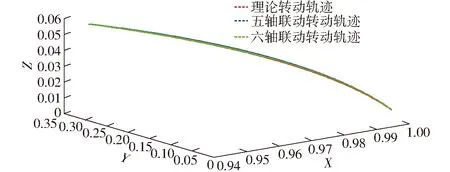
图6 抛光轮轴线矢量转动轨迹Fig.6 Trajectory of polish wheel axis vector
由于图5和图6均为三维曲线,为了直观表示在五轴联动和六轴联动情况下抛光轮中心点平动轨迹误差,根据式(12),绘制出该误差的变化曲线,如图7所示。
同样,根据式(17),绘制出在五轴联动和六轴联动情况下,抛光轮轴线理论转动轨迹与实际转动轨迹之间夹角误差的余弦值,如图8所示。

图7 抛光轮中心平动轨迹误差Fig.7 Trajectory errors of polish wheel center point

图8 抛光轮轴线转动轨迹误差Fig.8 Trajectory error of polish wheel axis vector
如图5、7所示,以抛光轮中心点理论运动轨迹作为参考,五轴联动下实际运动轨迹的最大误差为0.864 mm;六轴联动下实际运动轨迹的最大误差为0.189 mm,即误差更小。同样,如图6、8所示,以抛光轮轴线矢量理论转动轨迹作为参考,六轴联动下抛光轮轴线转动夹角误差明显小于五轴联动情况。结合式(18)可知,五轴联动下实际转动轨迹的角度最大误差为0.049 7°,对应接触点轨迹误差为0.131 mm;六轴联动下实际转动轨迹角度最大误差为0.013 9°,对应接触点轨迹误差为0.037 mm,即误差更小。因此,结合式(20)可知,机床在六轴联动下的实际加工轨迹误差比五轴联动下的实际加工轨迹误差更小。
图4所示的工件其他部分加工同样按照式(33)产生机床各个联动轴的运动量,从而实现加工轨迹误差的优化,其实际加工过程如图9所示。

图9 六轴联动数控机床实际加工过程Fig.9 Polishing process of six-axis linkage CNC machine tool
工件在机床中分别以五轴联动和六轴联动对工件进行抛光加工,通过白光干涉仪分别测量工件同一处两种联动模式下的表面抛光效果,结果如图10所示。图10a为五轴联动的抛光结果,工件的表面粗糙度为1 303.594 nm;图10b为六轴联动的抛光结果,其表面粗糙度为909.270 nm。图10a的表面粗糙度更大,且存在多处欠抛现象(黑色条纹),即表面粗糙度一致性更差。由于两种联动模式下理论加工轨迹和其他抛光条件均相同,可见,通过对加工轨迹误差的优化,降低了工件的抛光表面粗糙度,同时得到了均匀一致性更好的抛光表面。该优化方法可以应用于实际抛光加工。
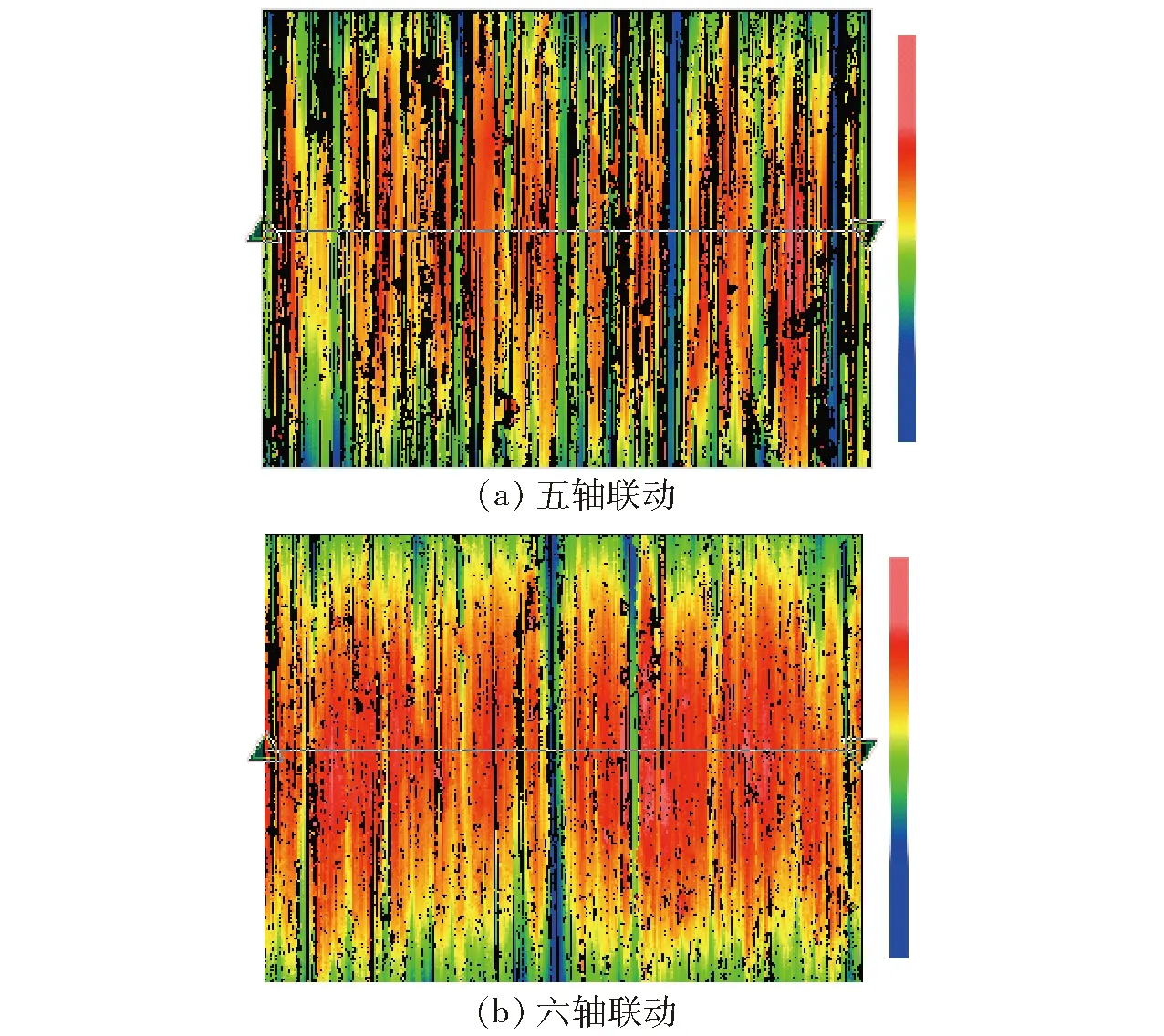
图10 两种联动模式的抛光加工结果Fig.10 Polishing results of two linkage modes
5 结论
(1)建立了具有3个平动联动轴和3个旋转联动轴的六轴联动数控机床运动学模型,研究了其冗余联动特点。
(2)在研究机床加工轨迹误差产生机理的基础上,提出了以冗余旋转联动轴的运动优化刀具中心点运动和刀具轴线转动的方法,降低了加工轨迹误差,提高了抛光加工质量。
