基于伪码锁相技术的高精度测距修正方法

(北京空间飞行器总体设计部，北京 100094)

星间通信及距离测量是实现卫星组网编队飞行及自主定轨的关键技术。测距精度直接影响自主定轨精度，最终影响终端用户的定位精度。双向单程测距体制(DOW)要求发送端和接收端严格按照统一的时钟节拍进行信号的发送与接收，即要求发送端按照本星时频单元输出秒脉冲的上升沿发送测距信号，接收端按照本星时频单元输出秒脉冲的上升沿(秒脉冲上升沿即为测距时刻)采样测距信号，计算传播延时产生伪距测量。但是由于测距接收机中跟踪测量FPGA的工作时钟与时频单元的时钟非同源，所以跟踪测量FPGA依据工作时钟计数形成的秒脉冲上升沿会早于或晚于时频单元秒脉冲的上升沿，又由于两个时钟的异步关系，也不可以用时频单元秒脉冲上升沿直接对测距信号进行采样(FPGA内部会产生亚稳态)，所以需要测量出这两个脉冲之间的时间差来对测距值进行修正。经调研，目前国内外测量两个脉冲时间差方法[1]包括直接计数法，模拟内插法、延迟内插法、不同长度导线测量法及游标法等。

(1)直接计数法，用高速时钟对这两个脉冲进行采样，测量两个脉冲之间的时钟个数。本方法测量精度较低，在十几纳秒范围内，而且由于是异步关系所以采样会存在亚稳态，导致存在整周期模糊度问题，而测距接收机要求的测量精度在百皮秒量级，所以不适用在高精度测距接收机中。

(2)模拟内插法，本方法基于电子计数方法，对待测脉冲填充计数时钟。需要使用模拟电路进行充放电，还要使用更高频率时钟进行采样，由于模拟电路容易受工作环境高低温影响，并且采用的更高频率时钟还是存在一个时钟周期的不确定度，测量精度依旧不高，在测距接收机中不适用。

(3)延迟内插法，原理是通过大量具有相同延时间隔的传输单元串联组成，开始信号进入延迟单元后启动监测结束信号，当开始和结束信号均进入延迟单元后统计通过的延时单元来计算时差，这些功能目前采用专用集成电路设计来实现，仅采用FPGA很难实现。

(4)不同长度导线测量方法需要过多的外围硬件，并且测量值易受工作环境高低温影响，仅采用FPGA很难实现。

上述几种测量方法要么是测量精度不满足需求,要么就是电路复杂，温度稳定性不好，均不满足使用要求。本文提出了一种测距修正方法，即采用伪码锁相跟踪环技术实现时钟同步与时差测量，优点是工作环境简单，资源占用少，采用1片FPGA就可以实现，能够与片内其它功能模块进行集成设计，减少接口传递，具有测量随机误差小、精度高(可达皮秒量级)，不易受高低温影响等优点。

1 测距原理

1.1 接收机工作环境

星间测距接收机接收时频单元输出的3个时频信号，如图1所示。这3个时频信号分别是10 MHz时钟信号，10.23 MHz时钟信号以及秒脉冲信号。其中，10 MHz时钟信号是由原子钟产生，10.23 MHz称为时频基准信号，由10 MHz时钟进行频率综合后产生。秒脉冲信号由10.23 MHz时频信号计数产生，整秒时刻输出脉冲。接收机将10 MHz进行倍频产生80 MHz给跟踪测量FPGA使用。

图1 跟踪测量FPGA外围时钟使用情况Fig.1 Clock environment of tracking FPGA

10.23 MHz是由10 MHz原子钟合成得到，但是长时间工作过程中，10 MHz时钟会由于元器件老化等原因导致频率发生微小变化，最终导致10.23 MHz发生变化。为了保证时频基准信号频率的准确性，当10 MHz频率发生变化时，需要对频综的参数进行调整，使得时频基准信号依然保持10.23 MHz输出，时频基准信号调整范围为±1.5 Hz。10.23 MHz时钟调整的过程，实际上是对10.23 MHz与10 MHz的频率与相位关系进行调整，上述两个时钟的异步关系导致跟踪测量FPGA工作时钟80 MHz与10.23 MHz信号所产生的秒脉冲也是异步的。

1.2 星间测距及修正测量

双向单程测距是指两颗卫星依据自己时间基准在本星时频单元的秒脉冲上升沿时刻按照10.23 MHz频率相互发送测距信号，同时在秒脉冲上升沿时刻互相测量对方信号的到达时刻，随后通过互相交换对方的伪距测量值以达到消除钟差实现真实距离的测量。

例如，A星按照秒脉冲上升沿，周期的发送测距伪随机码。经过空间传输后到达B星，B星通过测距接收机接收,并在本星时频单元输出秒脉冲上升沿时刻锁存跟踪环路恢复出来的A星发来伪码整数码片计数与小数码片计数，随后再按照式(1)计算出空间传播的时间。如果双星时间完全同步，则计算出来的就是双星之间真实距离，否则计算出来的就是伪距。跟踪测量FPGA取得的测距值t和双星之间的伪距T(单位：s)为

(1)

式中：tint为锁存的整码片计数；tfrac为锁存的小数码片计数；w为伪码跟踪环路NCO的累加器位宽，Δt为双星时差。

图2所示为跟踪测量FPGA的测距时刻与时频单元秒脉冲上升沿时刻不一致时形成的测距误差，式(1)中的t即是图1中的伪码传播延时，B星应该的测距时刻是整1 s时刻，而实际的测距时刻是80 MHz时钟产生的测距时刻，所以需要扣除td，则修正后的伪距T′为

T′=1-(t-td)=T+td

(2)

式中：td为时间修正量。

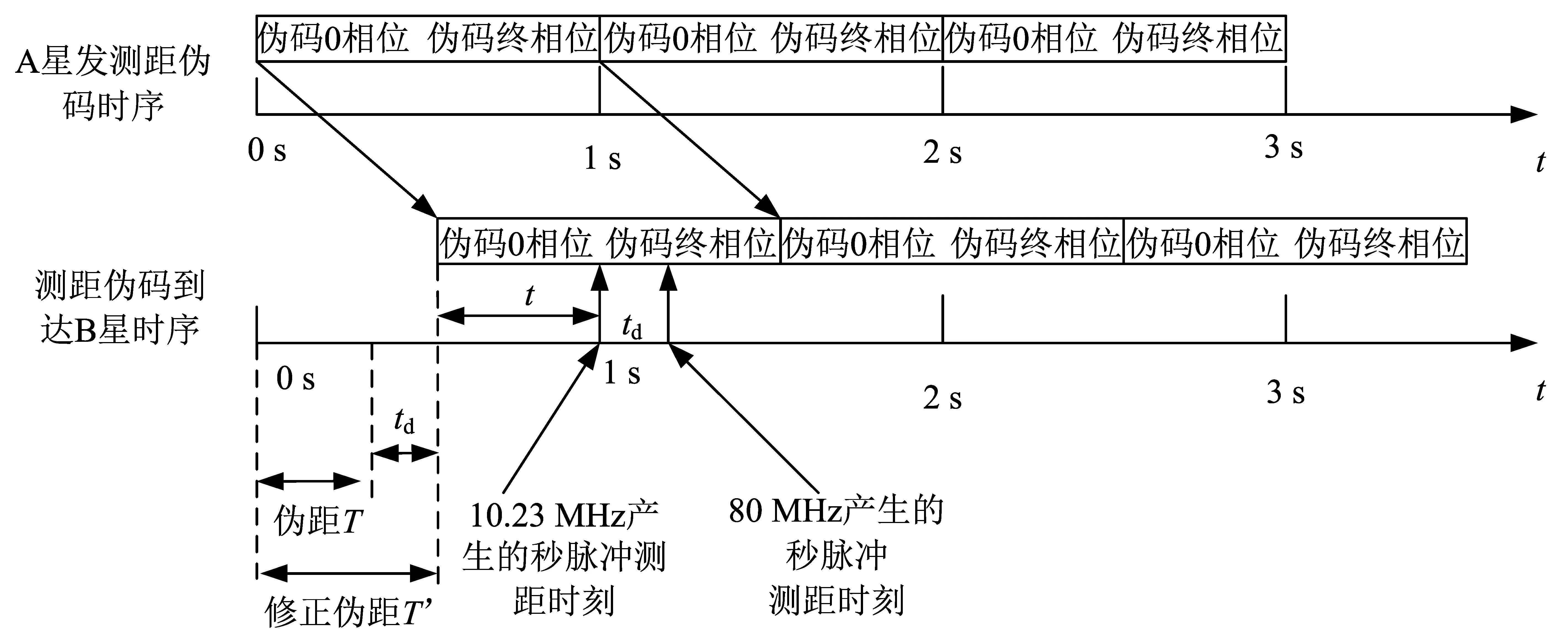
图2 A星发B星收测距码空间传播时序Fig.2 Ranging code propagation in space between two satellites

2 伪码锁相的修正量测量技术

2.1 锁相跟踪环路及实现方法

跟踪测量FPGA的输入信号10.23 MHz与80 MHz是异步关系，为了实现两个时钟产生的秒脉冲同步，首先必须同步这两个时钟，在时钟同步的前提下可以实现测量脉冲之间的同步。本文介绍了一种采用伪码锁相技术实现80 MHz与10.23 MHz信号进行同步的方法，跟踪环路FPGA实现见图3。时频单元输入的10.23 MHz与秒脉冲信号作为输入驱动“伪码序列A生成器”产生周期为1 s的伪随机序列A。由80 MHz作为工作时钟驱动“本地NCO”产生片内10.23 MHz，与外部时频输入的秒脉冲共同驱动“伪码序列B生成器”产生一个周期为1 s的伪随机序列B，序列A与序列B的生成多项式一样，随后序列B与序列A送“鉴相器”进行相关运算产生鉴相误差，并送“环路滤波器”，滤波器的输出来调整“本地NCO”来实现环路的跟踪。当环路锁定后就实现了片内10.23 MHz信号与时频单元输入10.23 MHz信号的同步，此时这两个时钟产生的秒脉冲就实现了同步。

图3 FPGA跟踪环路实现框图Fig.3 Tracking loop diagram in FPGA

2.2 伪码序列生成器

二进制数随机序列具有很重要的特点，它具有良好的自相关性[2]。一个二进制数随机序列x(t)的自相关函数，Rx(τ)定义为

(3)

其中，x(t-τ)是x(t)在时间上向右平移τ后得到的波形，所以自相关函数Rx(τ)是检查x(t)与它自身平移后的波形x(t-τ)两者之间的相似程度。二进制数随机序列的自相关函数Rx(τ)在原点中心呈一个三角形。这表明当τ=0时，波形完全重叠，具有最大相关性，如图4所示。

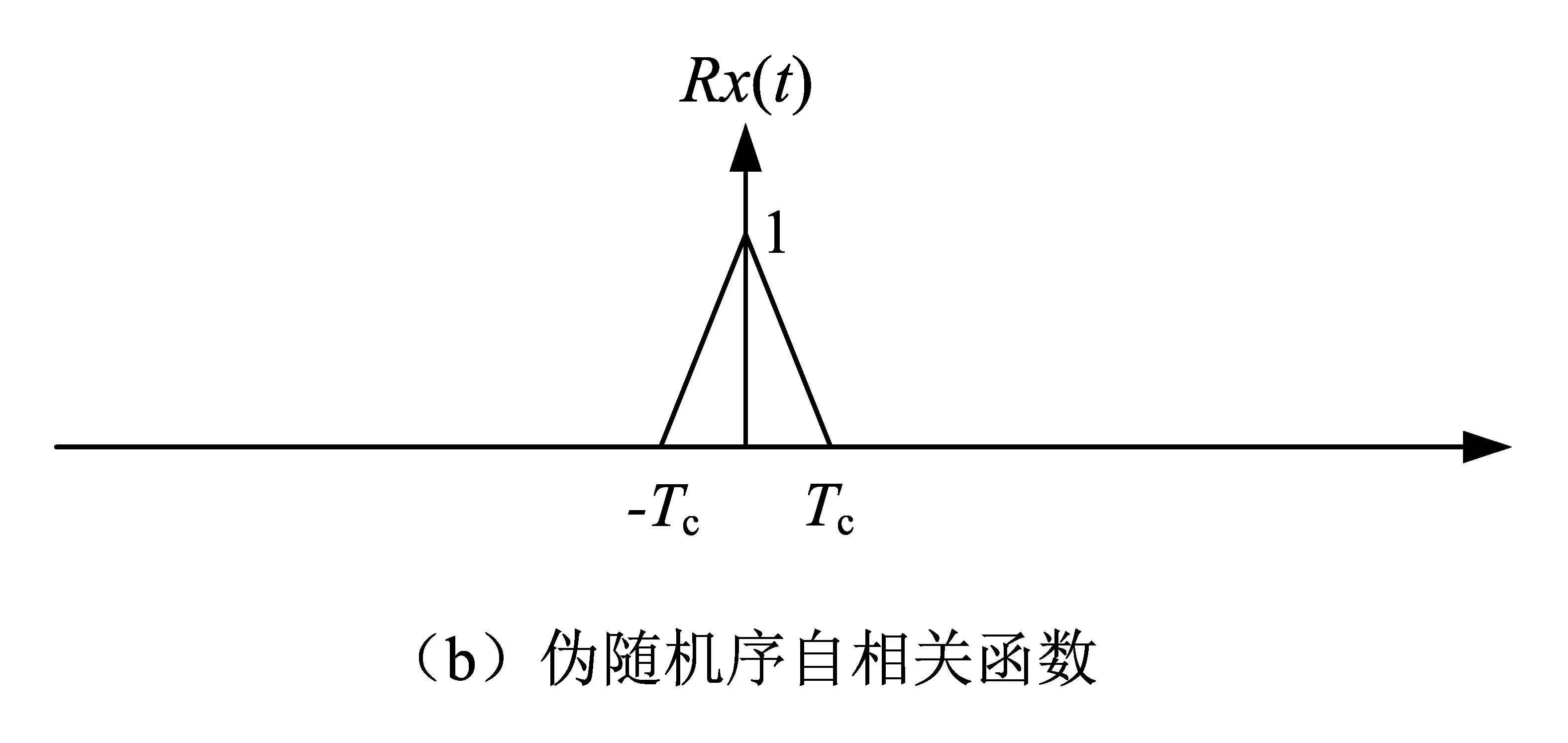
注：Tc为码元宽度。

图4 伪随机序列及自相关函数

Fig.4 PN code and the autocorrelation function

本应用中，选用的伪码生成多项式为：x24+x7+x2+x+1(初相全一)。

2.3 鉴相器

鉴相器是实现两个异步信号频率与相位的比较，输出相位误差。时频单元送来的10.23 MHz信号驱动伪码生成器A，由秒脉冲信号上升沿置码生成器初相状态。片内NCO输出的10.23 MHz信号驱动本地伪码生成器B，由80 MHz时钟采样到输入秒脉冲上升沿后置伪码序列B初相状态。上述两个伪码生成序列在80 MHz的工作时钟节拍采样下进行相关运算，整秒时刻(或毫秒时刻)输出相关结果作为鉴相误差送环路滤波器。令：x(n)是对伪码序列A的采样序列，y(n)是对伪码序列B的采样序列，则相关运算可以表示为

(4)

式中：N是相关运算累加长度,n是序列编号。

伪码跟踪采用延迟锁定跟踪算法，在生成伪码序列B时产生一路超前(Early)码Be，一路即时(Prompt)码Bp和一路滞后(Late)码Bl，其中超前码Be的相位相比即时码Bp的相位超前π相位，滞后码Bl相对即时码Bp滞后π相位。当跟踪锁定时，即时支路的伪码与输入的伪码同频同相关系。鉴相算法可以采用式(5)计算。归一化的鉴相误差计算公式为[3]

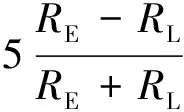
(5)

式中：RL为迟路相关结果；RE为早路相关结果。

相关时常决定了鉴相误差的精度与随机误差，长时间的相关运算可以减小鉴相随机误差，提高鉴相精度,但同时又会影响环路的收敛时间。当对收敛时间要求并不严格的场合，可以尽量延长鉴相时间。本例中由于采用的是1 s周期的伪随机码，故鉴相时间可以选择1 s。

2.4 环路滤波器

环路滤波器采用理想二阶环路，可以对频率阶跃信号无误差的跟踪。环路滤波器经双线性变换后的数字化实现形式如图5所示。

图5 理想二阶环路数字化模型Fig.5 Ideal two order loop filter

令ts为环路鉴相误差更新频率，ε为环路阻尼系数，bl为环路带宽。则环路无阻尼振荡频率为

ωn=(8εbl)/(4ε2+1)

(6)

令环路增益K=KaKb，Ka为鉴相增益，Kb为压控增益，fs为数控振荡器NCO的工作频率，w是NCO的累加位宽，则Ka=1/π，Kb=2π×fs/2w。通过式(7)、(8)[4]可以计算出环路滤波器的积分系数与直通系数[4]。

积分系数为

(7)

直通系数为

(8)

2.5 时差提取与测量

数控振荡器是通过调整累加值大小来控制累加器溢出频率的快慢来形成不同震荡频率的。令：NCO累计器位宽是w，输出的中心频率是fo，工作频率为fs，则频率控制字fc为

(9)

式中：R(·)表示四舍五入。则在某个溢出时刻，相位累加器溢出后剩余的值为

Pi=M(kfc,2w)

(10)

式中：M(·)表示取模运算，k是满足kfc>2w的最小整数。

Pi均匀地分布在[0，fc)范围内，当Pi为零时，本地NCO恢复出的10.23 MHz的上升沿与时频单元输出的10.23 MHz的上升沿完全对齐，当溢出值不为零时，本地NCO恢复出的10.23 MHz的上升沿将会滞后时频单元输出的10.23 MHz的上升沿，并且滞后时间的多少由溢出值Pi来度量。

图6是使用32 bit相位累加器，80 MHz工作时钟，中心频率10.23 MHz，连续300多个采样点NCO累加器溢出时刻的相位值转换为时间的仿真曲线。

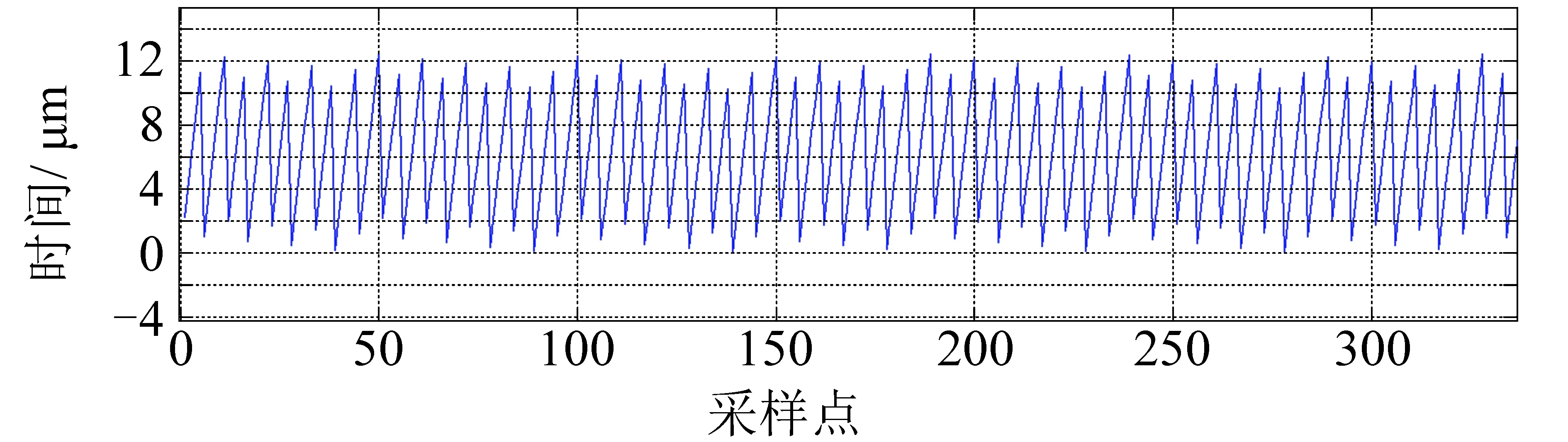
图6 NCO溢出值的分布Fig.6 Overflow value of NCO

将溢出值转换成时间(单位：s)为

(11)

从图6中可以看出，时间呈锯齿状均匀分布在[0，12.5]ns范围内。在取得td后再依据式(2)可以计算出修正后的伪距。

2.6 测量误差分析

上述锁相跟踪环路的相位测量误差源包括相位抖动和动态应力误差，而造成相位抖动误差源主要分为热噪声、机械振动引起震荡频率抖动以及艾兰均方差三种[5-6]。综合起来，环路跟踪相位抖动方差如式(12)所示。

(12)

采用上述方法设计的伪码锁相跟踪环路当环路锁定后本地NCO输出的10.23 MHz时钟与时频单元输入的10.23 MHz信号实现了同步，并且由这两个时钟各自生成的秒脉冲也实现了同步。两个秒脉冲上升沿的相位差由式(11)给出，相位差的随机抖动方差由式(12)给出。

3 FPGA设计实现

上述伪码锁相同步及时差测量方法采用FPGA实现，分成如下几个模块，实现框图见图7。

(1)时频单元时钟驱动伪码产生模块。该模块输入时频单元时钟10.23 MHz与秒脉冲信号，并按照2.2节的伪码生成多项式产生伪码序列。伪码的初相时刻由秒脉冲信号的上升沿置位。

(2)本地伪码产生模块。该模块输入NCO产生的10.23 MHz信号与启动信号，由启动信号上升沿置伪码相位初相。

(3)乘法运算模块。对时频单元驱产生的伪码与本地伪码模块的早路伪码、迟路伪码按照80 MHz的时钟频率采样相乘输出。

(4)积分清零模块。该模块对乘法运算模块的输出进行积分累加，每次清零脉冲到达时刻输出累加值同时清零。

(5)鉴相模块。该模块依据公式(5)进行相位检测，输出鉴相误差。

(6)环路滤波器模块。该模块依据2.4节描述的滤波器进行设计。

(7)本地伪码NCO模块。该模块工作时钟80 MHz，根据“开始跟踪脉冲”信号启动输出10.23 MHz时钟信号以及积分清零脉冲。本模块受环路滤波器输出的误差控制字动态调整输出频率，达到对时频输入的10.23 MHz时钟的锁相跟踪。

(8)锁定检测模块。依据伪码自相关函数的特性，如果积分时常为1 s，则早(或迟)支路为准支路相干积分的一半，即是40 000 000，适当考虑余量，当早(或迟)支路相干积分大于20 000 000时认为环路锁定，此时输出的时差测量值有效。

(9)等待计数器模块。当本地伪码与输入伪码码相位相差一个码片以上时，环路无法跟踪锁定。通过设置等待计数器延迟本地伪码初相生成时刻，保证本地伪码与输入伪码相位基本对齐，跳过捕获过程直接进入跟踪状态。

本设计是星间通信测距接收机基带模块通信测量FPGA程序中的一个小模块，FPGA选用Xilinx公司的XC4VSX55芯片，该模块的使用资源情况见表1。

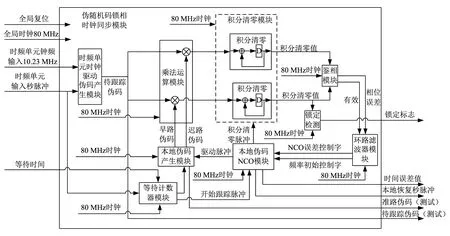
图7 FPGA设计实现框图Fig.7 Project diagram of FPGA

逻辑资源使用数量/个可用量/个百分比/%Slice registers4251228800Slice LUTS4711228800Full used LUT-FF pairs29560149

4 仿真及测试验证情况

4.1 跟踪环路仿真

为了验证伪码锁相环路及环路跟踪参数设计的正确性，采用系统工作时钟80 MHz，设置时频单元输入时钟10.23 MHz+1 Hz，采用周期1 ms的伪随机序列进行跟踪，相关积分时间1 ms。设计环路带宽为5 Hz、7 Hz、9 Hz、11 Hz的情况下，环路跟踪仿真曲线如图8所示。从图8中可以看出，环路带宽大收敛速度快。由于频差在环路的快捕获带内，所以均经过一个周期的频率捕获后进入了相位跟踪[7]。

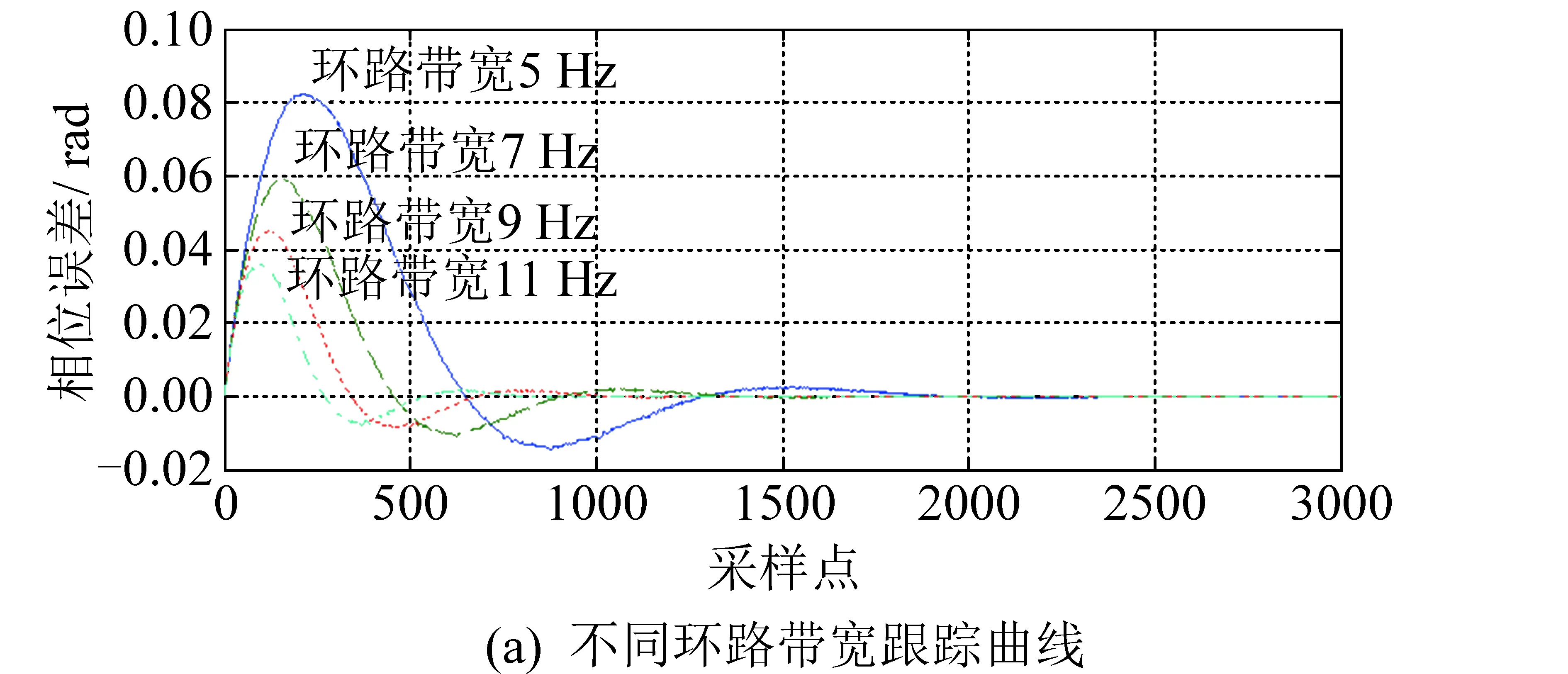
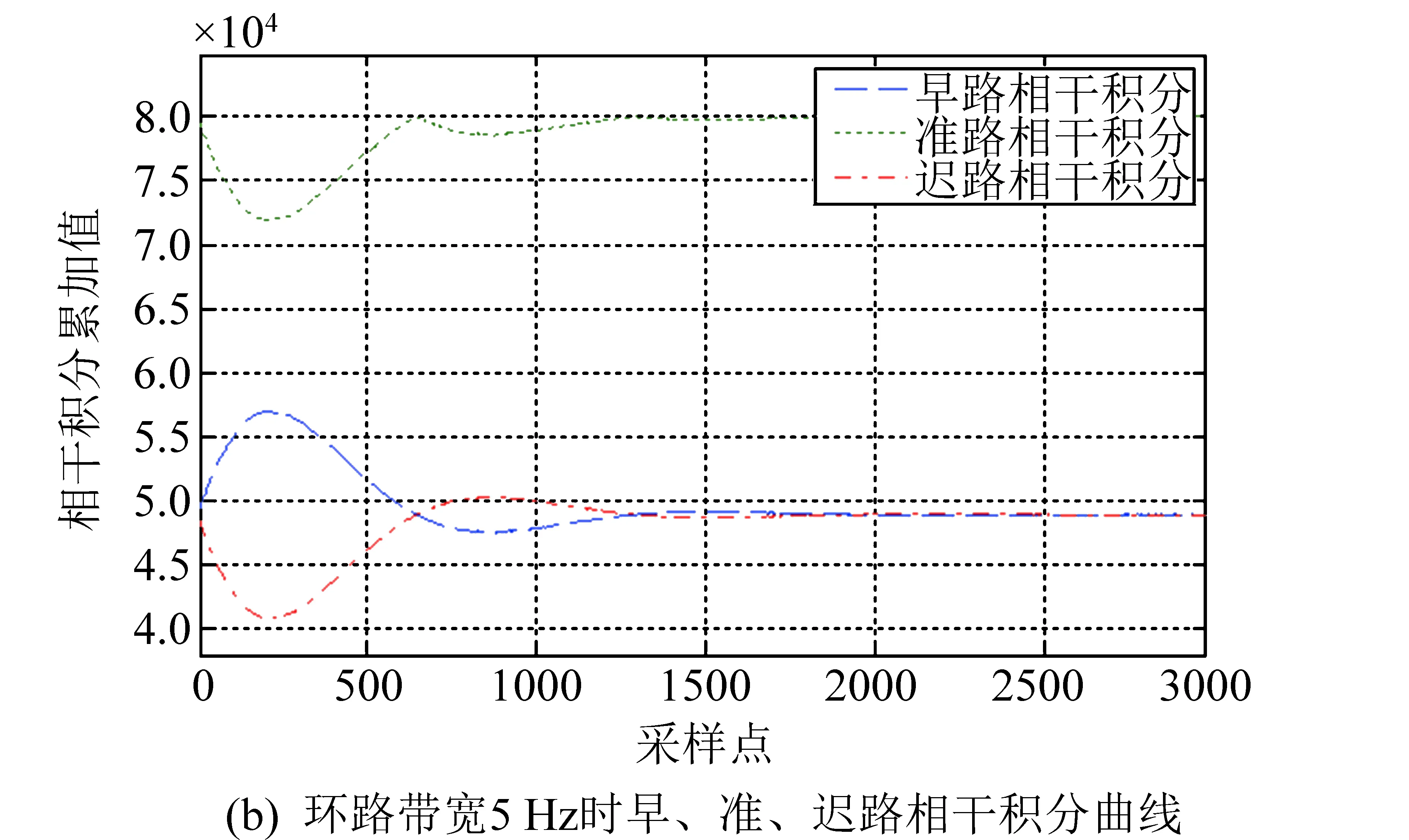
图8 1 Hz频差时不同环路带宽下的跟踪曲线Fig.8 Trace curve of 1Hz frequency difference in different loop width

设置同一环路带宽5 Hz，不同的输入频差0.2 Hz、-0.6 Hz、1 Hz、-1.5 Hz情况下进行仿真，环路的跟踪特性如图9所示。从图9中可以看出，当输入不同频差信号时环路均可以跟踪锁定，并且当锁定后准支路的相干积分值基本维持在2倍的早路与迟路的相干值，与理论计算预期一致。

在不同输入频偏下当环路锁定之后，NCO的溢出值表征的是本地恢复出的秒脉冲与时频单元输入的秒脉冲之间的时间差，可以作为修正量对测距值进行修正。将溢出值转换为时间(见图10)，时间差呈锯齿状均匀分布在0～12.5 ns之间。

图9 当输入不同频差信号时环路的跟踪曲线Fig.9 Trace cure in different frequency difference

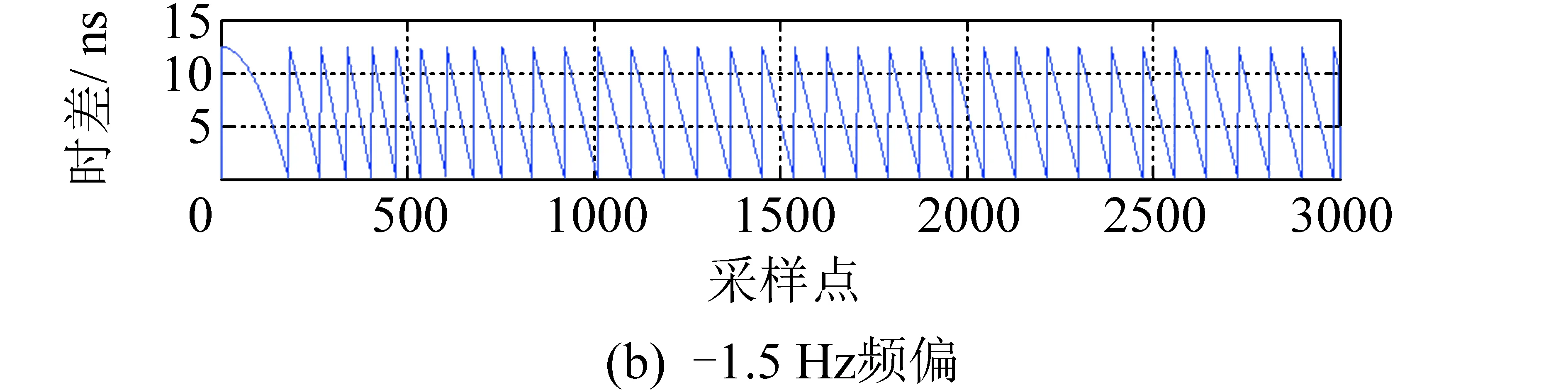
图10 当输入不同频差信号时NCO溢出时刻Fig.10 Overflow of NCO under different frequency difference

4.2 FPGA测试验证

测试环境硬件组成包括时频单元，两个测距接收机基带模块(模拟A/B双星)，以及测距接收机的单检设备。时频单元输出的10 MHz与10.23 MHz信号同时接上述两个基带模块。当10 MHz与10.23 MHz相位完全固定时，这两个时钟产生的秒脉冲相位保持稳定，所以测距曲线稳定。此时调整10.23 MHz为10.23 MHz+1 Hz再观察补偿前与补偿后的测距值，如图11所示。

从图11的测试曲线可以看出，调整时钟频率后，由于两个时钟产生的秒脉冲相位相对滑动，导致测距值呈锯齿状波动，补偿后测距值稳定。此时信号的C/N0=56.5 dB·Hz。补偿后测距随机误差为0.306 ns，由于补偿值的随机误差是皮秒量级，为星间无线电测距随机误差的1%，所以对最终测量结果无显著影响。

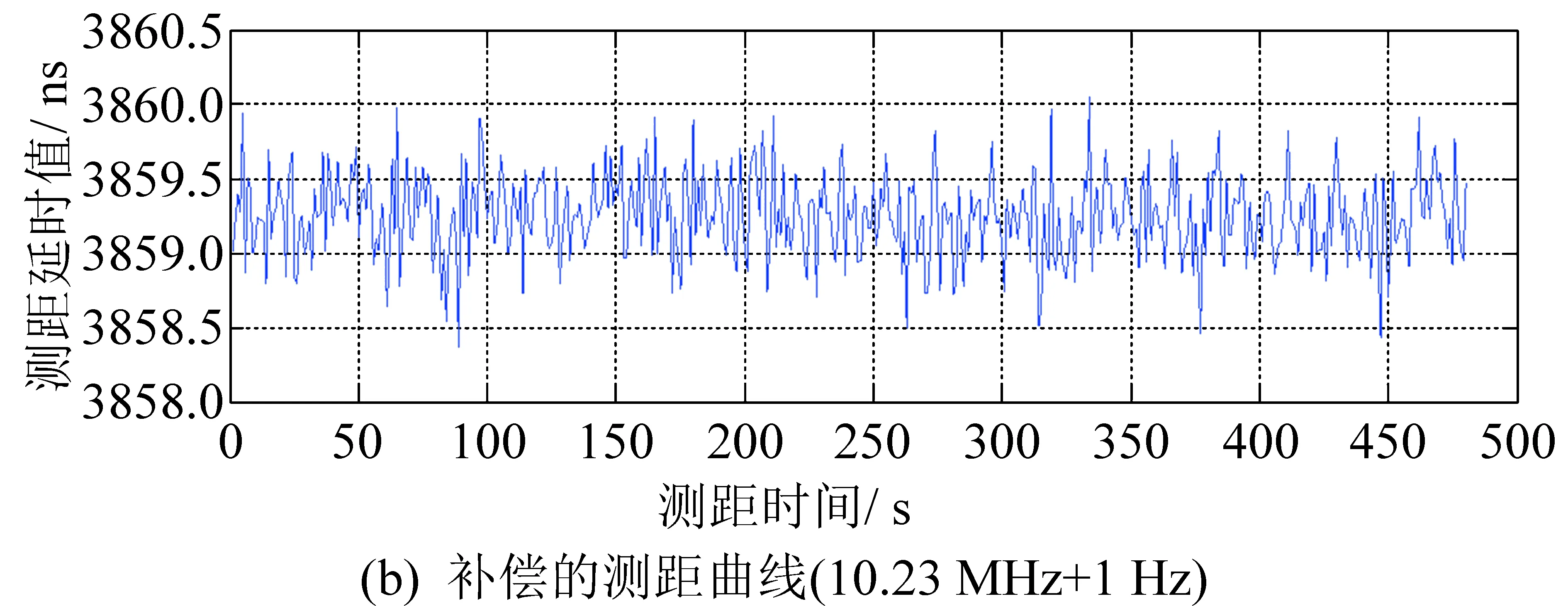
图11 补偿前与补偿后的测距延时值Fig.11 Range values before and after compensation

5 结束语

本文提出了一种采用伪随机码跟踪锁相方法对两个不同源时钟产生的异步测距时刻进行同步的方法。跟踪环路使用的伪随机码为截断的小M序列，并利用伪随机序列良好的自相关特性，采用延迟锁定环路计算鉴相误差，环路滤波器采用理想二阶环，可以无误差的跟踪频率阶跃变化。最终实现FPGA工作时钟对时频单元10.23 MHz信号的良好跟踪。经分析与测试，验证了跟踪精度高达到皮秒量级，修正后对原始测距值随机误差影响较小，满足高精度星间测距的要求。