探测器月地转移入射变轨策略优化设计

(北京空间飞行器总体设计部，北京 100094)

在月球采样返回任务或载人登月任务中，都可能涉及探测器从环月轨道出发，通过变轨机动进入月地转移轨道。月地转移入射(Trans-Earth Insertion，TEI)变轨策略的优化设计是一个经典的月球探测轨道设计问题，也是我国实现探测器月球采样返回必须突破的一项关键轨道设计技术。

国内外诸多学者已对探测器月地转移入射变轨策略的设计进行了深入的研究[1-5]。文献[1]针对从环绕月球的圆形轨道出发进入逃逸轨道的问题，研究了一脉冲和两脉冲变轨方案，其中第一个脉冲在环绕轨道上施加，而两脉冲变轨方案的第二个脉冲是在月球影响球边界上施加的，主要用于改变轨道平面。文献[2]研究了从椭圆轨道上采用最优三脉冲变轨方案实现给定逃逸双曲线超速矢量，得到了计算变轨序列的分析公式，然后采用数值方法进行轨道优化。文献[3]则考虑了从环月轨道出发进入月地转移轨道的问题，先针对一脉冲变轨方案推导得到了变轨位置和变轨量的分析求解公式，然后在此基础上推广讨论了在环月轨道通过三次变轨机动，实现从环月轨道进入月地转移轨道的算法。文献[4-5]则考虑了在月球探测任务燃料预算紧张情况下的月地转移变轨策略，通过一次环月轨道变轨机动进入低能月地转移轨道，之后在日地或地月拉格朗日点附近执行一次速度增量很小的轨道机动，来瞄准地球再入条件。上述月地转移入射一脉冲、两脉冲、三脉冲和低能月地转移轨道方案在速度增量、月地转移飞行时间等方面有显著差别，所以各有优缺点和工程适用范围。本文在综合月地转移入射多方案研究成果的基础上，对各方案分别进行分析，发展了文献[1,3]中月地转移入射一次变轨策略的优化算法，并根据工程设计中的实际需求，针对月地转移入射变轨策略从一脉冲改为两脉冲的问题进行了研究，提出了月地转移入射两脉冲变轨策略的优化算法。另外，为了应对因故障原因导致的错过月地转移窗口、剩余推进剂余量不足等情况，需要制定轨道故障预案，所以还对月地转移入射三脉冲方案和低能月地转移轨道展开了讨论，得到了一些对工程设计有重要参考价值的结果。最后，对这些方案进行了比较分析，确定了各方案的优缺点和适用条件，可供开展月球采样返回任务时制定月地转移入射变轨策略参考。

1 问题的提出

在月球采样返回任务的月地返回阶段，轨道器和返回器的组合体(简称组合体)在环月轨道上等待数天，在预定的月地转移日期，通过轨道器发动机实施变轨机动，组合体进入月地转移轨道，其终点是位于地球大气边界的再入点。工程设计中发现，月地转移入射如果采用一次变轨方案，为了减少重力损耗和减轻热控、电源等分系统的负担，变轨时间不能太长，这就需要采用大推力发动机；另一方面，由于月地转移入射时组合体的质量比采样返回任务初期时小了很多，若采用大推力发动机，对组合体结构柔性振动的激励较大，难以实现高精度轨道控制，存在较大轨道控制风险。为此，考虑将月地转移入射一次变轨机动的方案改为分成两次执行，这样每次变轨的时间不长，可以采用较小推力的发动机实施。

月地转移入射两脉冲方案的轨道示意如图1所示，其中第1次变轨的目标是从环月近圆轨道进入周期约为8 h或12 h的大椭圆轨道，第2次变轨的目标和月地转移入射一脉冲方案类似，即瞄准理想的再入点参数：再入点高度、再入角、再入点轨道倾角、预定着陆点地心矢径和轨道面夹角(0°)。

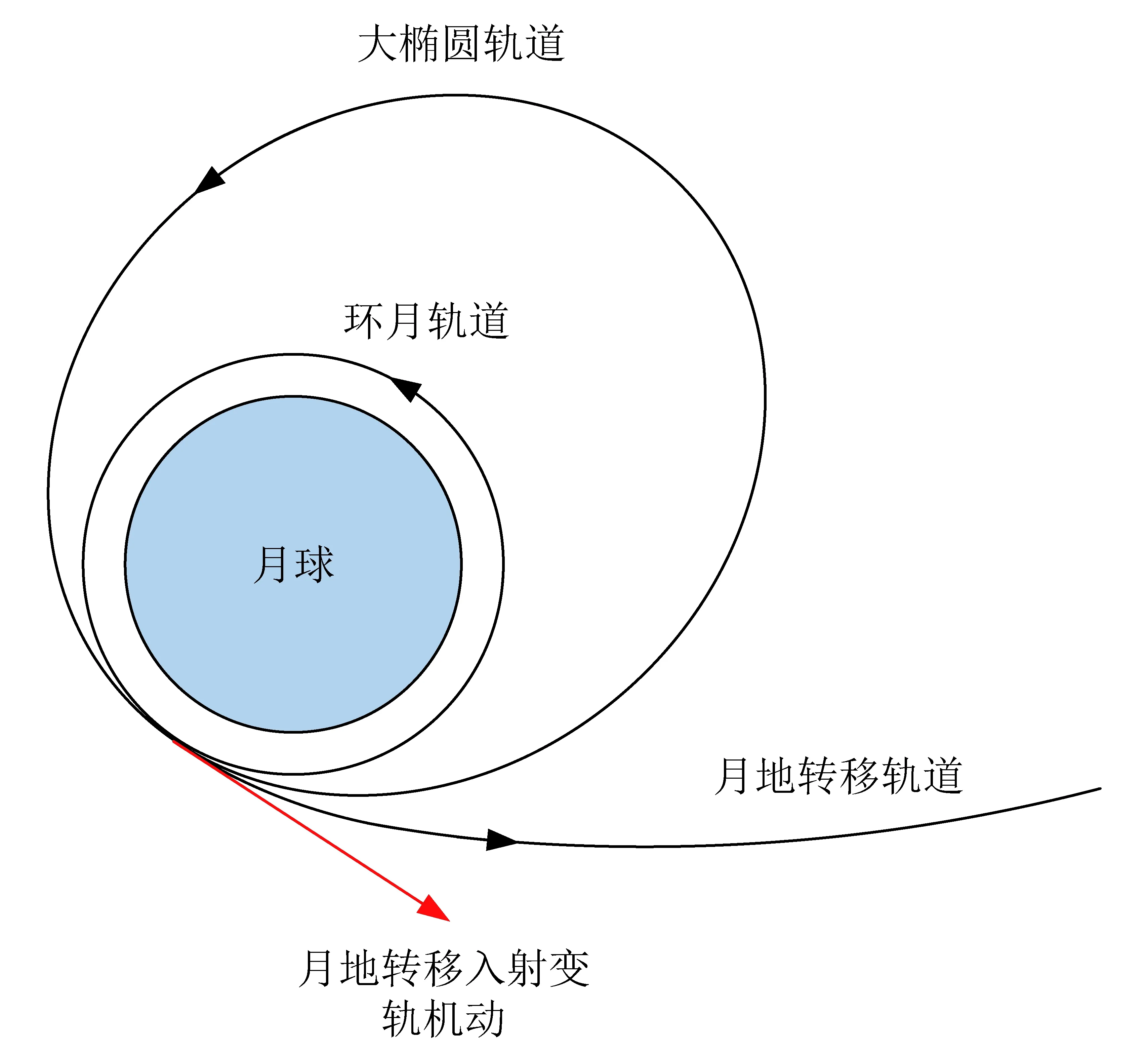
图1 月地转移入射两脉冲轨道方案Fig.1 Two-impulse TEI strategy illustration

从以上讨论可以看出，这里的两脉冲方案和文献[1]中的两脉冲方案考虑的出发点是不同的。由于这里的两脉冲方案是由一脉冲方案演变而来的，其两次变轨速度增量的方向和一脉冲方案变轨速度增量的方向基本一致。其中，第1次变轨的控制目标是轨道周期(调相)，是1对1的控制(设计变量是变轨速度增量大小)；第2次变轨是4对4的微分修正控制，其设计变量和控制目标均与一脉冲方案类似，即设计量为变轨速度增量的3个分量和到达再入点的时间，控制目标是前面提到的4个再入参数的理想数值。

本文的主要目的就是对月地转移入射一脉冲和两脉冲方案的变轨策略进行详细讨论，并进一步拓展讨论三脉冲方案和低能月地转移轨道方案，在此基础上对不同方案的适用范围开展比较分析。

2 月地转移入射一次变轨策略

2.1 月球逃逸双曲线超速的近似计算

图2为月地转移轨道在地心天球上的示意图，图2中给出了月地转移轨道起点(远地点)的月球位置和月地转移轨道终点(近地点)的位置。其中，远地点的月球位置矢量可以根据月球星历得到，而近地点的位置矢量可以认为近似沿远地点月球位置矢量的反方向，近地点高度可取60 km。

图2 月地转移轨道在天球上的投影Fig.2 Moon-to-earth transfer on celestial sphere

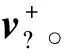
另一方面，当月地转移轨道终点的位置矢量是严格沿着远地点月球位置矢量的反方向时，如果没有其它约束，Lambert问题有无穷多个解。为得到唯一解，可以取月地转移轨道终点的位置矢量稍微偏离远地点月球位置矢量的反方向(图2中转移轨道终点B稍微偏离终点A)，同时使得月地转移轨道的倾角近似为理想的再入点轨道倾角。

2.2 一次变轨优化算法

参考图3，初始环月轨道参数已知，设轨道角动量为h0，月地逃逸轨道的轨道角动量为hf，月地转移轨道和环月轨道的交点(变轨点)月心矢径为r1，月地转移入射变轨速度增量矢量为Δv1。在下面的讨论中，下标0表示已知初始环月轨道参数，下标f表示月地转移轨道参数，下标1表示变轨点参数。如果未作特殊说明，后续轨道参数均为在月心惯性系下定义的参数。

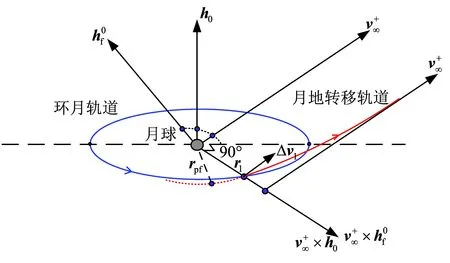
图3 月地转移入射一次变轨Fig.3 One-impulse TEI strategy

(1)

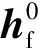
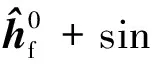
(2)

上标 ^ 表示单位矢量，下同。

1)计算变轨点轨道参数

(3)

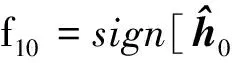
(4)

(5)

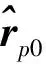
2)计算月地转移轨道相对月球的轨道参数

(6)

(7)

(8)

3)计算变轨量Δv1

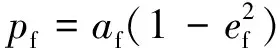
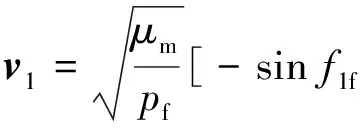
(9)

遍历θ(0°-360°)后，取变轨速度增量最小对应的Δv1为最佳变轨量，最佳变轨纬度幅角为u10=ω0+f10，其中ω0为已知环月轨道近月点幅角。

需要说明的是，在月地转移入射一脉冲方案变轨策略优化设计中，需要在入射前若干天额外引入一次调相机动来保证在指定入射时刻取得最佳月地转移入射纬度幅角。另外，测控分析对月地转移入射变轨策略的实际工程应用是十分必要的，这是因为测控分析能给出月球对测控站可见的时间范围(测控弧段)，其开始和结束时间可作为规划月地转移入射变轨策略的天然时间参考[9]。在下一节关于两次变轨策略的讨论中将给出测控分析的进一步说明和算例。

2.3 计算过程

总结以上讨论，并考虑实际工程中的测控条件等约束，得到月地转移入射一脉冲方案变轨策略优化设计的计算过程如下：

(1)根据测控条件分析结果，选择月地转移入射变轨机动的时刻；

(2)根据测控条件分析结果，在月地转移入射变轨机动前若干天选择调相机动时刻；

(3)根据前述基于二体模型的分析算法，计算最佳月地转移入射纬度幅角u10和变轨量Δv1；

(4)采用精确轨道动力学模型和4对4微分修正，求解变轨量Δv1的精确值；

(5)在月地转移入射纬度幅角u10附近小步长调整变轨纬度幅角，求得月地转移入射纬度幅角u10和变轨量Δv1的优化解；

(6)根据调相机动时刻、月地转移入射时刻和最佳月地转移入射纬度幅角u10，计算调相脉冲；

(7)重复迭代计算(3)→(4)→(5)→(6)→(3)→……，直到最佳月地转移入射纬度幅角u10收敛。例如，当连续两次迭代计算所得u10数值的差别小于0.1°，即可认为迭代计算收敛。数值分析表明，通常迭代2～3次即可，本算法具有良好的收敛性。

3 月地转移入射两次变轨策略

3.1 基于测控条件分析的深空探测轨道设计

在深空探测实际飞行任务中，通常要求变轨机动在地面测控监视下进行，且变轨前留有足够的测控时长用于定轨、注入等操作。为此，本文提出了一种基于测控条件分析的深空探测轨道设计方法[9-13]。其基本思想是：月球、火星等自然天体(中心点)对地面测站可见的开始时刻和结束时刻可作为进行天体探测轨道设计的天然时间基准；在轨道设计中，变轨机动的时间应当安排在天体中心点对测站可见的时间段内，并为变轨前后的定轨、注入等操作留有足够的测控时长；尽量把轨道机动的位置(纬度幅角)设置在测控可见对应的纬度幅角范围内，以便变轨机动在地面测控监视下进行。

例如，假定月地转移入射的最佳日期是2019年1月4日，由于月球轨道测控条件大约每25 h重复一次[9]，在采用月地转移入射两次变轨方案时，为了保证两次变轨均有国内站测控监视且变轨前留有足够的测控时长，可安排第1次变轨在2019年1月3日实施，而第2次变轨在2019年1月4日实施。计算月心对国内站的测控可见时段，结果见表1。

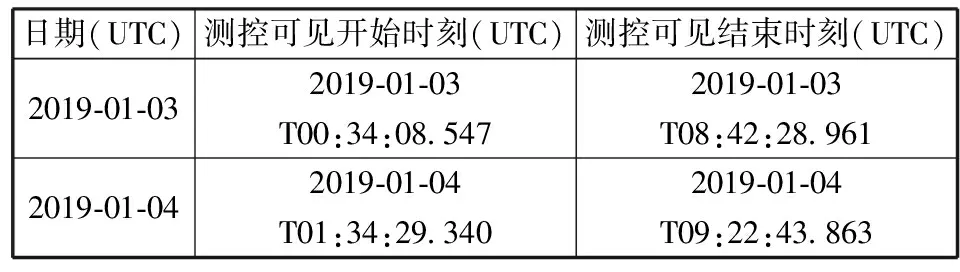
表1 月心对国内站的测控可见时段

根据表1中的测控分析结果，可以安排第1次变轨在2019年1月3日的测控可见开始时刻(2019-01-03T00:34:08.547)之后，当探测器飞至前述最佳变轨纬度幅角时执行，控制目标是在第2次变轨时刻取得最佳变轨纬度幅角，而第2次变轨时刻可取为2019年1月4日的测控可见开始时刻(2019-01-04T01:34:29.340)加上30 min，即2019-01-04T02:04:29.340。

3.2 计算过程

前面得到了月地转移入射一次变轨方案的最佳变轨纬度幅角u10和变轨量Δv1，在此基础上可进一步计算月地转移入射两次变轨方案的优化变轨策略。月地转移入射两脉冲方案变轨策略优化设计的计算过程如下。

(1)取第2次变轨时刻和月地转移入射一次变轨方案的入射时刻相同(当天测控可见开始时刻加上30 min)，变轨量初值为一次变轨方案变轨量的1/2，即Δv1/2；

(2)根据测控分析结果，安排第1次变轨在第2次变轨前一天的测控可见开始时刻之后，当探测器飞至变轨纬度幅角u1=u10时执行，变轨速度增量大小的初值取为|Δv1|/2，变轨速度增量的方向(方位角α、高度角δ)和Δv1相同，控制目标是在第2次变轨时刻取得纬度幅角u2=u10(调相)；

(3)采用高精度轨道动力学模型和微分修正，计算两次变轨的精确解，其中第1次变轨为1对1微分修正，第2次变轨和一次变轨方案类似，为4对4微分修正；

(4)若有必要，可考虑在以上u1、α、δ和u2所取初值附近小范围内进行调整(优化)，使得总的速度增量∑Δv最小。

可以看出，由于在两次变轨方案中的第1次变轨具备调相功能，无需像一次变轨方案那样在月地转移入射前若干天额外增加一次调相机动。

3.3 算例

假定月地转移入射的最佳日期是2019年1月4日。表2和表3给出了前面所述优化算法流程对应的月球采样返回任务月地转移入射具体数值计算结果。表2中x、y、z表示位置坐标，vx、vy、vz表示速度三分量。可以看出，两脉冲方案总的速度增量只比一脉冲方案略微有所增加，前面提出的在一脉冲方案计算结果基础上进行两脉冲方案变轨策略优化计算的算法是有效的。

表2 环月轨道参数(月心J2000)

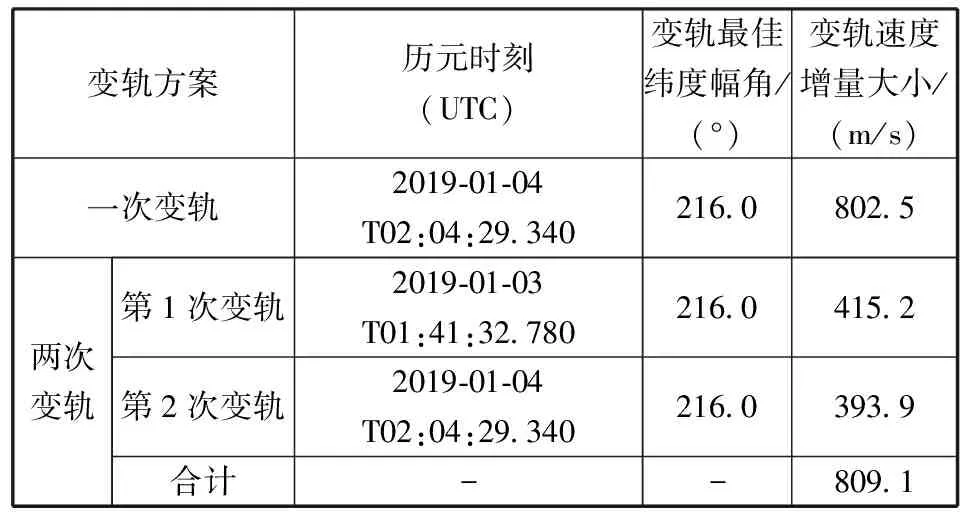
表3 一次变轨方案和两次变轨方案分析结果比较

4 月地转移入射三次变轨策略

在月球采样返回任务实施过程中，如果由于故障原因错过了预定月地转移窗口，但仍需要尽快实施月地转移返回地球，这种情况下环月轨道面和月球逃逸轨道面的非共面度(夹角)较大，为避免大的月地转移入射轨道面修正速度增量，可以考虑采用三脉冲入射方案：先在环月轨道的适当位置实施第一次(平面内)变轨，抬高远月点高度，进入周期为若干天的大椭圆轨道；然后，当探测器到达远月点时，实施第二次变轨机动，其主要目的是调整轨道平面，使得调整后的轨道面与逃逸轨道面一致；最后，当探测器飞至近月点时，沿速度方向施加速度增量，探测器进入逃逸轨道(即月地转移的开始段)[3]。三脉冲入射方案适用于非共面度(夹角)过大条件下的转移入射，其基本原理是利用远月点速度较小的特点来减小平面调整的速度增量需求。三脉冲入射方案的具体设计方法简述如下。

4.1 二体分析

需要说明的是，在三脉冲入射方案中，第二次变轨所在的远月点高度和第三次变轨所在的近月点高度是设计量。下面讨论中选择近月点高度为200 km，远月点高度可根据选择的大椭圆轨道周期计算。

4.2 摄动模型分析

在上述二体分析中，仅考虑了月球对探测器的中心引力。在工程应用设计中，还需要考虑月球非球形引力摄动、太阳和地球三体引力摄动等摄动因素的影响。这些摄动因素会导致实际飞行轨道偏离理想的圆锥截线，从而对具体设计结果包括速度增量等产生较大影响，详见下面讨论。在摄动模型分析中，首先需要进行测控条件分析，确定执行Δv3的具体时间，并使得探测器在国内站共视条件开始时刻后飞至f10时执行Δv1。

为了保证在预定时刻执行Δv3，需要通过调整Δv1的大小进行调相，而Δv1的方位角(α1)和高度角(δ1)采用二体设计值；为了保证执行Δv3的近月点高度为200 km和瞄准再入点参数，采用Δv2的3个分量、Δv3的大小(Δv3方向为速度方向)和再入点时刻为微分修正设计变量。总起来说，采用Δv1的大小、Δv2的3个分量、Δv3的大小和再入点时刻瞄准Δv3执行预定时刻、近月点高度200 km和再入点参数，是一个6对6微分修正过程。

在摄动模型分析中，还可以调整f10、α1和δ1，对总的速度增量进行优化，使得总的速度增量∑Δv最小。

4.3 大椭圆轨道周期的选择

表4给出了针对某算例开展月地转移入射三脉冲方案设计时，分别选择大椭圆轨道周期为1～5天的设计结果。

从表4中可以看出，当选择大椭圆轨道周期为4～5天时，远月点平面修正机动速度增量的二体设计结果和摄动模型差别很大。参考图4，图4中虚线表示二体模型分析中第二次变轨前后的轨迹，实线为摄动模型下的轨迹，显然摄动模型下第二次变轨前后的轨道面变化比二体模型下大幅增加。究其原因，这是因为当大椭圆轨道周期较大导致远月点高度过大时，地球的摄动影响增强，三体效应导致环月轨道面发生“翘曲”，从而需要修正的轨道面非共面度大幅增加的缘故。

综合考虑，建议选择大椭圆轨道周期为2～3天。另外，从分析结果可以看出，环月轨道面和月球逃逸轨道面的夹角较大时(推迟时间返回)采用月地转移入射三脉冲方案，所需速度增量比夹角较小时(预定时间返回)采用一次或两次变轨方案多100 m/s左右。但事实上，夹角较大时采用一次或两次变轨方案所需速度增量远大于三脉冲方案，例如图4中环月轨道面和月球逃逸轨道面的夹角约为45°，采用一次或两次变轨方案时，平面修正所需速度增量的分量高达1200 m/s。所以，在比标称设计增加100 m/s速度增量可以接受的条件下，由于采用三脉冲方案有助于扩大月地返回窗口，在故障条件下是较好的选择。

表4 月地转移入射三脉冲方案大椭圆轨道周期的选择

值得一提的是，为避免大的轨道面调整导致的过多推进剂消耗，还可以考虑实施月球逃逸机动，绕飞地月拉格朗日点L2，并再次实施逃逸机动返回地球的月地转移轨道方案。这一方案和三脉冲原理类似，这里不展开讨论。

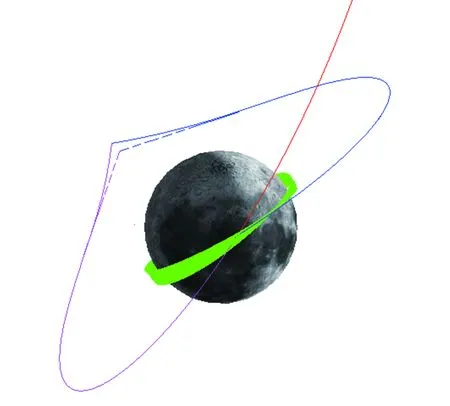
图4 翘曲现象Fig.4 Warping phenomena

5 低能月地转移轨道

除了上面讨论的常规月地转移入射轨道方案外，还可以考虑低能月地转移轨道方案。月球采样返回任务飞行阶段多，出现应急轨道故障的风险较大[10]。例如，如果新型运载火箭发射探测器入轨时偏差较大(特别是半长轴不足)，就需要在地月转移段消耗较多的推进剂来进行轨道修正；类似这样的轨道故障处置可能导致月地转移入射前发现推进剂余量已不足以完成预定的月地转移变轨任务，这种情况下可以考虑采用低能月地转移轨道方案作为应急轨道预案。低能月地转移轨道方案充分利用地月和地日拉格郎日点的特性来节省月地转移能量，月地转移入射仅需630 m/s左右的速度增量，比前面讨论的常规月地转移入射方案节省150 m/s～200 m/s速度增量，所以在剩余推进剂余量不足以实施常规月地转移方案时，可以采用低能月地转移轨道方案来保证月球采样返回任务的完成。不过，转移时间需要增加到3～5个月。

图5展示了月球采样返回任务轨道设计中的一条典型低能月地转移轨道。

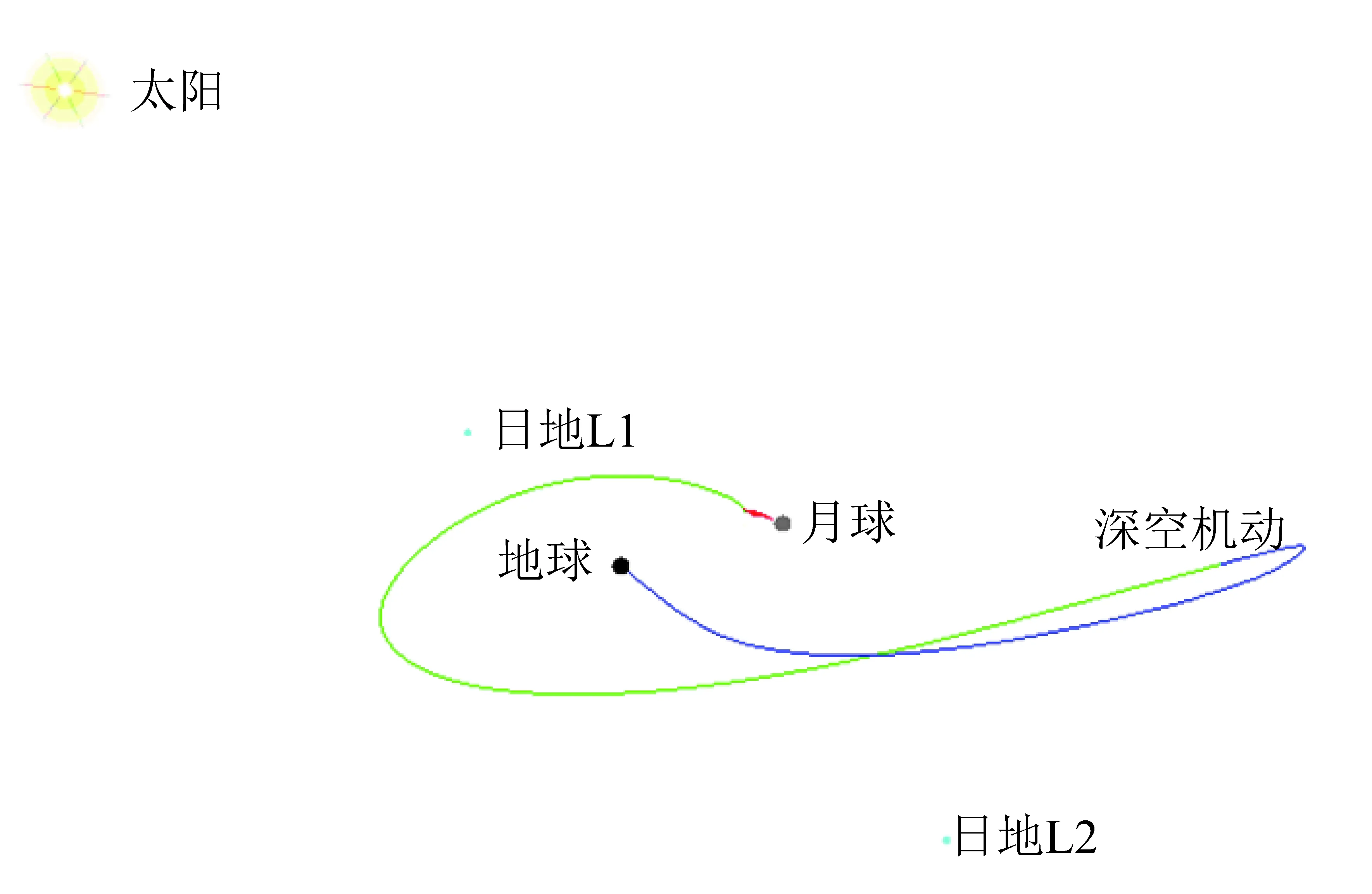
图5 月地低能转移轨道示意图Fig.5 Low energy moon-to-earth transfer

低能月地转移轨道设计的基本步骤是：①完成月球轨道交会对接和样品转移后，探测器在近圆环月轨道上飞行，考虑沿着当前轨道位置的速度方向施加630 m/s左右的速度增量(TEI)，对施加速度增量后的轨道进行外推，直到探测器飞出月球影响球到达近地点，如果近地点高度较大(例如大于10 000 km)，则放弃考虑在当前环月轨道位置实施TEI，这样，按照一定时间步长(例如1 min)沿环月轨道逐步搜索若干天，直到找到实施TEI后轨道外推的近地点高度较小的环月轨道位置和时间；②在找到的候选低能月地转移轨道上的适当位置(例如TEI后第50天)增加一次深空机动(Deep Space Maneuver，DSM)，选取深空机动速度增量矢量三个分量和到达再入点时间作为设计量，采用4对4的微分修正精确瞄准理想再入点条件(类似前述常规TEI方案)；③综合考虑速度增量、测控、再入航程等设计约束，对环月轨道TEI时间、深空机动位置进行优化设计，得到低能月地转移轨道的优化设计。表5给出了低能月地转移轨道的一个典型设计结果。

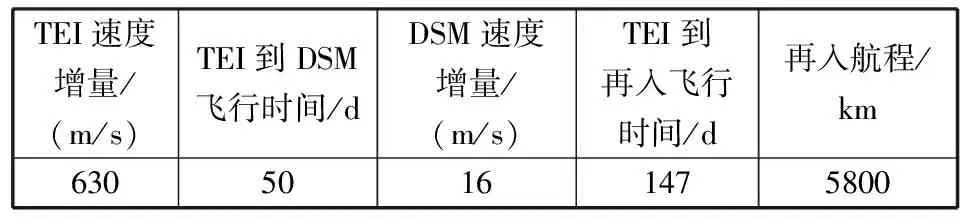
表5 低能月地转移轨道的典型设计结果

6 多方案比较分析

总结上述月地转移入射策略和轨道方案，得到多方案比较分析结果见表6。显然，考虑到我国开展月球采样返回任务的实际工程约束，任务正常实施情况下应采用月地转移入射两次变轨策略；如果由于故障原因错过了预定月地转移窗口，为避免大的月地转移入射轨道面修正速度增量，可以考虑采用月地转移入射三次变轨策略；如果由于故障处置导致月地转移前推进剂余量不足以完成常规月地转移入射和返回地球，应采用低能月地转移轨道。

表6 月地转移入射多方案比较分析

7 结束语

本文在改进月地转移入射一次变轨策略优化算法的基础上，采用基于测控条件分析的月球探测轨道设计方法，针对工程设计中提出的月地转移入射变轨策略从一脉冲改为两脉冲的问题进行了研究，给出了月地转移入射两脉冲变轨策略的优化算法流程。数值仿真计算结果表明：本文提出的优化算法是有效的，在工程设计中有重要应用价值。

另外，还针对月地转移入射三脉冲方案和低能月地转移轨道方案展开了讨论，分析表明：在月地转移入射需要进行大的轨道面调整的情况下采用三脉冲方案可以降低速度增量需求，有助于扩大月地返回窗口，月球采样返回任务中应用三脉冲方案时大椭圆轨道的适宜周期为2～3天；采用低能月地转移轨道比常规月地转移入射方案节省150～200 m/s速度增量，可以在常规方案所需剩余推进剂余量不足的条件下实施月地转移任务。论文提出的相关轨道方案的工程设计方法可应用于轨道应急预案的制定，是保障我国月球采样返回任务目标完成必需的关键轨道技术。