斜交45°现浇箱梁设计计算研究

万梦

招商局重庆交通科研设计院有限公司 重庆 400067

1 引言

由于项目路线跨越河道或者结构物，为减小对结构物的干扰或让桥梁顺适河道水流的流向，减小桥墩对河道的干扰同时能满足通航需求等原因，在选取桥梁方案时采用斜交布跨的方式较多。特别在高速公路、一级公路等建设条件下，在采用斜交的情况下不仅能减小对结构物和河道等因素的干扰，让路线平面更加的舒适，还可以减小桥梁长度、节省造价，所以斜交桥梁在上诉工程中应用广泛。在采用斜交梁桥时其受力特性和正交梁桥在受力上有着较大的差异，由于支座是斜向布置导致了其扭剪效应特别的突出。同时多跨的斜交连续梁结构受力比简支结构更为复杂，在计算时对应力，扭矩等控制更为的严谨。

坳头大桥为了适应路线变宽故采用四跨预应力连续斜桥箱梁。坳头大桥为整体式桥梁，桥跨布置为8×30m，共2联，本桥平、立面均处在曲线上，且桥跨处在变宽段，为了顺应浏源河的水流方向和满足行洪要求，桥跨斜45°布置。本桥上构采用预应力砼现浇箱梁桥，下构桥墩为桩柱式桥墩，桥台为重力式U型桥台和扩大基础。

2 斜桥受力特点

斜桥的主要受力特点：

（1）在桥梁的钝角位置的支座反力要大于其锐角位置的支座反力，同时锐角位置可能会出现支座脱空现象；斜交的角度越大，钝角处的支座反力和锐角处的支座反力相差越大。

（2）斜交时支座采用的是斜向布置，支座位置有很大的扭矩。

（3）斜交桥梁在弯扭耦合作用下，跨中弯矩要比正交桥梁要小，斜角角度进一步加大，其跨中弯矩折减越大；不过在弯扭作用下其跨中扭矩越越来越大。

（4）在活载、制动力、温度梯度、预应力效应等作用下，由于平面各个方向的位移不一致，使得平面出现弯矩，该作用让桥梁出现钝角方向朝锐角方向转动的趋势；如果出现了使桥梁伸缩出现限制的因素出现，如梁端伸缩缝缝隙被堵住和预留空间不足等这类的情况出现，箱梁转动的形势更大。

对于梁格法的横向刚度，Midas帮助文件中有如下描述：“对斜交桥梁多用梁格法进行建模。 可用斜交梁格或正交梁格来建模。对于斜交角度小于20时，使用斜交梁格是非常方便的。但是对于大角度的斜交桥，根据它的荷载传递特性，建议选用正交梁格，而且配筋时尽量沿正交方向配筋。”

坳头大桥的构件形式采用现浇预应力混凝土连续箱梁桥，跨径为2x（4x30）m，斜交角度45度，汽车荷载采用公路Ⅰ级，箱梁选用C50混凝土，箱梁顶板厚度为25～50cm，底板厚度为22～37cm，腹板厚度为50～80cm，腹板变化段长度为5m，桥面宽度为21.13～30.17m，箱室为三室变四室。桥梁横截面布置图如图1。

图一 箱梁跨中横截面布置图

3 结构建模分析

本桥采用Midas Civil建模分析，由于考虑到斜桥效应本文建立两种模型进行对比，分别为正交梁格模型和单梁模型，Midas模型如图二至图四所示

图二Midas梁格模型

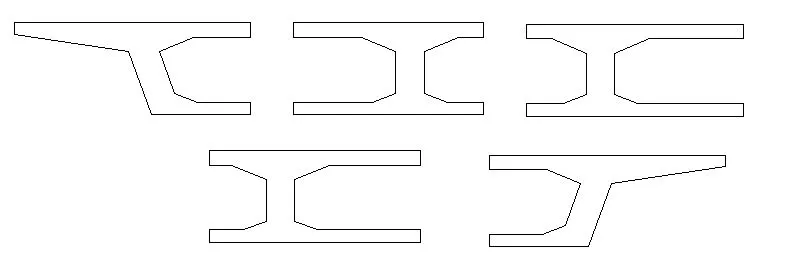
图三 划分的梁格断面

图四 Midas单梁模型

Midas梁格模型中把箱梁划分为五个纵梁，在实际的横隔板处用横梁模拟，横向连接梁间用虚拟横梁模拟，定义梁截面时选择梁上缘对齐方式，支座点的建立，可由梁上缘对应节点向下复制支座节点，并用刚性进行梁与支座的连接，支座沿桥轴线法向方向斜45度布置。Midas单梁模型中支座点的建立采用正交布置。

4 梁格模型与单梁模型计算分析

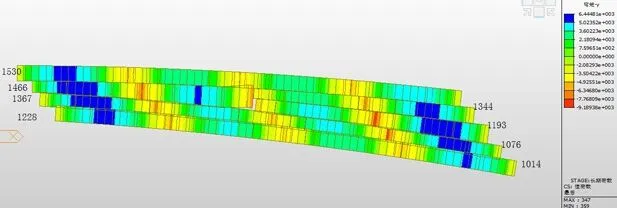
图五 梁格模型弯矩M-y图

图六 单梁模型弯矩M-y图

图七 梁格模型扭矩图

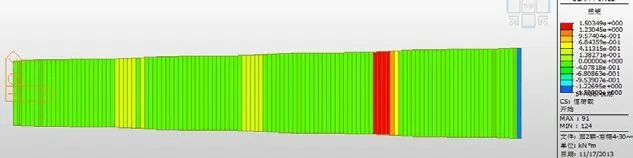
图八 单梁模型扭矩图

经计算梁格模型弯矩M-y在第一跨支点为-2628.8KN*m，第一跨跨中为6352.5KN*m；第二跨支点为-8288.5KN*m，第二跨跨中为5057.3 KN*m；第三跨支点为-6318.2 KN*m，第三跨跨中为4244.6KN*m；第四跨支点为-9189.4KN*m，第四跨跨中为6444.8KN*m。单梁模型弯矩M-y在第一跨支点为-4205.5KN*m，第一跨跨中为23108.9KN*m；第二跨支点为-37033.7KN*m，第二跨跨中为13137.4KN*m；第三跨支点为-21781.3KN*m，第三跨跨中为18442.1KN*m；第四跨支点为-48691.7KN*m，第四跨跨中为31949.2KN*m。

经计算梁格模型扭矩在第一跨支点为1563.4KN*m，第一跨跨中为2684.3KN*m；第二跨支点为951.0KN*m，第二跨跨中为1262.0KN*m；第三跨支点为1320.0KN*m，第三跨跨中为923.0KN*m；第四跨支点为1054.7KN*m，第四跨跨中为2168.3KN*m。单梁模型扭矩计算结果几乎为0。

由上述可以看出，用单梁模型的跨中和支点的弯矩M-y远大于梁格模型的弯矩M-y，但是单梁模型中扭矩几乎处处为零，这样子不符合斜桥的弯扭耦合作用计算依据。所以在计算斜桥时应采用正交梁格模型。

根据梁格模型结算结果0号支点左侧墩顶反力为634.6kN，右侧墩顶反力为1367.3 kN；1号支点左侧墩顶反力为1249.7 kN，右侧墩顶反力为2855.3 kN；2号支点左侧墩顶反力为1445.8kN，右侧墩顶反力为1682.0kN；3号支点左侧墩顶反力为1079.2 kN，右侧墩顶反力为2855.3kN；4号支点左侧墩顶反力为2739.5 kN，右侧墩顶反力为1374.1kN。

斜交箱梁在自重作用下的支座反力不相同，锐角处出现较小反力，当斜交角度越大时，锐角处有可能出现支座脱空现象，斜交箱梁最大弯矩向钝角方向靠拢，同时在自重作用下，斜交箱梁存在较大的扭矩，具有明显的空间受力特性，这些效应的大小与斜交角度大小也有很大的关系，斜交角度越大，上述效应就越大，一般来说斜交角度小于20时，对于斜交桥的上述影响可以忽略，如果斜交角度超过20度，就必须考虑上述效应的影响。

5 预应力效应

预应力效应见图九。

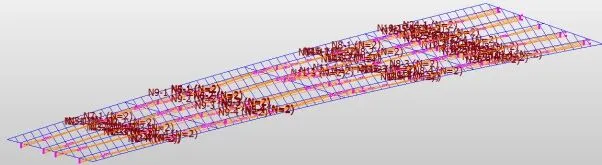
图九 梁格法预应力束形

计预应力与不计预应力时墩的反力取用该桥两端的支座反力，其具体数据如下所示。

计预应力时左侧墩顶的反力总和为6214.2KN，右侧墩顶的反力总和为8296.6KN；不计预应力时左侧墩顶的反力总和为6270.1KN，右侧墩顶的反力总和为8307.6KN。计预应力时1号支点左侧墩顶反力为949.7KN, 右侧为2855.3KN；不计预应力时1号支点左侧墩顶反力为538.5KN, 右侧为4292.7KN。

由此可以得出：（1）由预应力效应引起的反力在合计的情况下几乎与未计预应力效应下一样，但是在各个支座上的有着区别。（2）预应力效应使得各个支座的反力更加的均匀。（3）预应力效应对于斜交在各个支座上桥梁钝角大和锐角处小的现象没有影响。

6 结论

梁格法是桥梁结构空间分析的一种有效方法，由于其具有基本概念清晰，易于理解和使用的特点，在进行斜桥分析时往往采用该方法。斜交梁桥在弯扭耦合作用下其扭矩，剪力等要比正交梁桥大，空间受力特性更加明显，故对于斜角角度大于15度的梁桥不宜采用单梁法来建模计算，而应该采用更为合理的梁格法来进行分析。

根据前几节的结论，斜交梁桥其自身的受力特性，在耐久性和经济性等因素上有所欠缺。不过在设计上可以通过采用梁格法进行计算后对于跨径较大的桥梁增加跨中横隔板，在横梁处加大横向钢筋的配置，增设钝角和锐角角域钢筋等措施来缓解上述因素。