微型力敏操纵杆的结构优化设计

李宝生, 王 政

(中国电子科技集团公司第四十九研究所，黑龙江 哈尔滨 150001)

0 引 言

微型力敏操纵杆是武器装备火控系统中操作手柄的核心敏感器件，将操作者作用力实时转化成电信号并输出到信号采集处理单元，辅助操作者完成目标搜索、瞄准与锁定、打击等任务[1]。随着力敏操纵杆的广泛应用，传统产品的一些缺陷逐渐暴露出来：1)敏感元件封装空间狭小[2]，导致工艺繁琐，成品率底，限制产能;2)采用刚性结构梁，导致操作手感僵硬，操作难度大。针对以上情况,本文对微型力敏操纵杆进行结构优化设计。

1 传感器原理简述

力敏操纵杆原理为：采用应变电测技术，测量悬臂梁微应变[2]，如图1所示，在悬臂梁根部封装敏感元件感应操作者作用力导致的悬梁应变，悬臂梁根部4个平面分别封装敏感元件，组成两组惠斯通半桥，如图2所示，实现对x，y轴向力的实时测量。

图1 悬臂梁示意

图2 敏感元件桥路连接

2 柔性梁设计

传统力敏操纵杆采用圆柱形刚性悬臂梁结构，如图3所示，梁根部磨4平面，用于封装敏感元件。这种结构形式的缺点是用于敏感元件封装的平面狭小，且所采用的刚性梁位移量很小。

图3 圆柱形刚性悬臂梁结构示意

为增加悬臂梁敏感元件的封装空间与拨动位移，设计了一种新型柔性梁结构，该结构由弹性元件与柔性元件组成。

2.1 弹性元件结构设计与力学分析

弹性元件采用外方内圆的空心结构，如图4所示，在增加敏感元件封装面积的同时满足应变值要求。弹性元件应变值为

(1)

式中ε为应变值，F为满量程载荷，L为在力臂长度，E为材料弹性模量，IZ为截面惯性矩，B为外方尺寸，A为内孔尺寸。

2.2 柔性元件结构设计与力学分析

2.2.1 柔性元件几何描述

为了在有限空间内实现操纵杆的拨动行程，柔性元件采用螺旋切口结构，如图5所示。柔性元件上端固定，下端作用横向力F时，将向右偏转，假设螺旋有n圈。在未受力的自然状态下，螺旋中心的轨迹为一等螺距螺旋线[3]，按照图示坐标，其参数方程为

(2)

式中 0≤t≤2nπ施力点坐标为(0,0，np+l)，在操作过程中，人手所感知的为该点的位移。

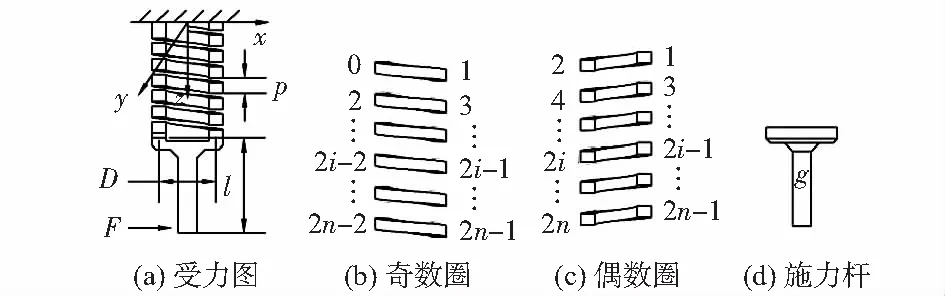
图5 柔性元件几何模型分解

2.2.2 柔性元件受力分析

可将柔性元件的几何模型分解为奇数半圈、偶数半圈及施力杆进行力学分析[4～6]。对每一个半圈与施力杆进行力学分析，构建柔性元件在横向力F作用下的变形计算模型，如图5所示。

在受到横向力F作用下，柔性元件将发生横向弯曲，在初始平衡状态下，图6中各截面所受载荷为

F21=F12=F32=…=F2i-2,2i-1=F2i,2i-1=F2i-1,2i=F2i+1,2i=…=F2n-2,2n-1=F2n,2n-1=F2n-1,2n=Fg,2n=F2n,g=F

(3)

各截面1所受扭矩为

T2i+1,2i=T2i,2i+1=F(2n-2i)p+Fl

(4)

(5)

式中T为各端点所受力矩；p为螺旋节距，在变形过程中不断发生变化，需要进行修正。

2.2.3 柔性元件形变量分析

当发生弯曲时，各端点在x-z平面内将发生位移，其中一个端点的位移包含两部分：横向平动产生的位移δ″和因截面扭转角φ产生的旋转位移δ‴。

1)截面扭转角

图6(a)示出的(0,1)段的螺旋半圈，是0端固定、1端自由的半圆形梁，根据莫尔积分，可求得1端截面对0端截面的扭转角φ1为

(6)

式中G为弹簧材料的切变模量；E为材料的弹性模量；μ为泊松比；I为螺旋截面对对称轴的惯性矩；Ip为螺旋的截面极惯性矩，由螺旋丝截面形状决定。

同理可得

(7)

(8)

2)平动位移的计算方法

如图6(a)所示(0,1)段半圆形，根据变形叠加及莫尔积分，可求得1端的位移，将求得的位移按夹角γ分解到x方向和z方向，夹角γ为半圆梁所在平面与x-y平面的夹角

(9)

可得1端在x方向的位移为

(10)

在z方向的位移为

(11)

同理，根据图6(b),(1,2)段半圆形梁的受力关系求得2端的位移，分解得到2端在x方向的位移为

sin(π+γ+φ1)

(12)

在z方向的位移为

cos(π+γ+φ1)

(13)

根据图6(c)所示(2i-2,2i-1)段半圆形梁的受力关系求得2i-1端的位移，分解得到2i-1端在x方向的位移为

(14)

在z方向的位移为

(15)

根据图6(d)所示(2i-1,2i)段半圆形梁的受力关系求得2i端的位移，分解得到2i端在x方向的位移为

(16)

在z方向的位移为

(17)

2n端所产生的平动位移量受之前的各点影响，其x方向平动位移为

(18)

z方向的平动位移为

(19)

3)截面扭转变形所产生的位移计算方法

2i-1端截面的偏转角φ2i-1导致该端点以后的螺旋线中心线发生偏转，角度为φ2i-1/2，螺旋线最后端点2n在x方向的位移为

(20)

z方向的位移为

(21)

2i端偏转角φ2i对引起2n端x向位移为

(22)

z向位移为

(23)

可得各端点偏转导致2n端x方向的位移为

(24)

z方向位移为

(25)

4)施力点位移

施力点的位移由螺旋末端2n端，与圆柱杆偏转位移组成，如图6(g)所示，施力点偏转角为

(26)

施力点的x方向位移为

(27)

施力点的z方向位移为

(28)

3 算例分析

常用力敏操纵杆有多种，如拇指力操作、手扳力操作等，根据使用方法不同其外形体积与性能参数各有不同，本文以拇指力微型操纵杆为例，目前市面上常用的拇指力微型操纵杆如图7所示。按以往经验，拇指力操纵杆量程为3LB(13.3N)，拇指易感知拨动行程不小于3 mm。

图7 拇指力用微型操纵杆实物与尺寸

为了增大弹性元件的应变值与柔性元件的拨动位移，选择强度高，弹性模量小的钛合金(TC11)为材料，弹性模量E=1.18×1011Pa，泊松比μ=0.3。根据产品空间并布局以量程需求，设计柔性机构的具体尺寸参数如图8所示，从图中可以得出，弹性元件力臂L=35.4 mm，贴片处外方尺寸B=2.6 mm，内孔直径A=2.1 mm。柔性元件螺距p=2 mm，共8圈，直径D=7.2 mm，螺旋丝截面宽b=2 mm，高h=1.4 mm，施力杆长度l=13 mm。

图8 柔性机构具体尺寸

由式(1)得，弹性元件应变值为1817×10-6，满足一般应变敏感元件的测量要求[7]。

计算柔性元件施力端位移量为

φg=0.089=10.2°

δg,x=3.8 mm

δg,z=-0.28 mm

施力杆所产生移动如图9所示。

图9 施力杆移动示意图

4 测试与误差分析

按图8完成柔性梁制作，并完成敏感元件封装，组装测试，如图10所示。采用图2的桥路连接敏感元件，采用±5VDC供电，加载3LB后测试桥路输出为1.48 V，x向位移为4.2 mm，z向位移-0.31 mm。

图10 组装及测试实物照片

可得应变值

(29)

式中u为桥路输出，为1.48 V；E为桥路单端电压，为5 V;K为敏感元件灵敏度，所选用的敏感元件灵敏度为170。

通过计算结果与测试结果对比可得，弹性元件的应变值与柔性元件的位移值均存在误差，应变值的误差产生主要由以下几方面：1)敏感元件灵敏度系数(K值)误差；2)机械加工误差，尤其是空心敏感部位形状误差直接导致应变值误差；3)敏感元件封装位置误差，弹性元件为悬臂梁原理，粘贴位置改变力臂长度，引起误差。

柔性元件位移误差产生由以下几方面：1)机械加工误差；2)计算过程忽略了微小的弹性元件与施力杆的弹性位移。

5 结 论

1)设计一种微型操纵杆用柔性梁结构，弹性元件采用空心结构，满足应变要求的前提下，有效增加了敏感元件的封装空间，柔性元件采用螺旋结构，施力过程中产生操作者易感知的拨动行程，改善操作手感。

2)为微型力敏操纵杆用柔性梁设计提供了一种有效的计算方法。