基于人工鱼群算法的光纤应变传感网络布置优化
2019-03-05刘雨博任洋洋
刘雨博, 任洋洋
(辽宁工程技术大学 机械工程学院, 辽宁 阜新123000)
0 引 言
目前在桥梁等结构复杂的大型工程结构中对于健康监测系统的应用非常广泛,在结构上布置的传感器能够实现监测的持续性,能够得到真实运行状态下的响应[1,2]。传感器布设系统在结构健康监测系统中发挥着非常重要的作用,监测结果在很大程度上受到传感器数量、位置以及类型的影响,在健康监测系统中传感器的优化布置是非常关键的组成部分。
在结构健康监测系统中传感器系统的作用是非常重要的。但在现场安装以及经济因素的影响下,在结构上只能安装数目有限的传感器。因此,越来越多的学者开始致力于研究如何利用有限的传感器来保证所获得的信息更大化,并开始致力于研究如何优化布置传感器[3,4]。
目前传感器布置优化研究的重点是针对用于结构振动情况监测的加速度传感器进行优化,很少有研究集中在优化用户安全评估的静力监测项目的应变传感器上,同时在获取应变传感器布置方案时通常以简单桥梁结构的整体为基础来进行[5,6]。因此,本文针对光纤应变传感网络,使用人工鱼群算法进行光纤应变传感器网络的节点布置优化研究。
1 光纤应变传感器原理
作为一种光学器件,光纤Bragg光栅(fiber Bragg gra-ting,FBG)具有波长选择特性。可以将其看作反射镜或者光滤波器,将宽带光注入到光栅中时,反射很窄的一部分符合光栅选择条件的光,保证其不穿透该光栅,光在光纤中的传播性质可以利用FBG改变,在反射特定波长光时避免其继续传播。如图1所示。
Bragg 波长λB为光纤Bragg光栅的波长选择条件,光栅周期Λ和有效折射率neff决定了Bragg 波长λB

图1 光纤传感基本原理
λB=2neffΛ
(1)
在不将温度因素考虑在内的基础上分析FBG的应变传感。由于光纤光栅波长只会受到应变的影响,有效折射率neff和光栅的周期Λ在弹光效应作用下发生变化,因此可以得到
ΔλB=2neffΔΛε+2ΔneffεΛ
=λBKεΔε=λBΔε(1-Pe)
(2)
式中 ΔΛε为在应变的作用下光栅波长漂移量,Δneffε为在应变作用下FBG光栅有效折射率变化量,Pe为[9]光纤的有效弹光系数。
2 光纤应变传感网络布置优化问题描述
常规研究中习惯将传感器检测区域设定为一个以传感器为圆心,半径为R的圆形检测区域。并认为在圆形区域内的检测信号被识别的概率为1,圆形区域外的检测信号被识别的概率为0。
圆形检测区域的假设不能完全适用于光纤光栅传感器,原因是由于光纤光栅传感器的特殊结构使得其轴向波长漂移和横向波长漂移量不相等,因此,急需要对传感器的安装角度进行考虑。
假设需要优化的光纤应变传感网络中设置有N个光纤应变传感器,待检测的信号设定为Pj,则该信号被传感网络检测到的概率设定为
(3)

当需要优化的光纤应变传感网络中存在M个待检测信号,则这些信号被传感网络检测到的概率以其概率均值表示[10]
(4)
则光纤应变传感网络布置优化的问题可描述为令信号未被传感网络检测到的概率均值最低
maxf1=1-PA
(5)
3 基于人工鱼群的布置优化算法
人们根据动物的行为研究出了人工鱼群算法,这种群体智能优化算法具有非常明显的优势。通过对随机、追尾、聚群以及觅食等海洋中鱼类群居行为的模拟人工鱼群算法就能够在解空间中找到最优解[11]。因此,本文使用人工鱼群算法进行光纤应变传感网络布置的优化研究。
定义觅食行为是第i条人工鱼的目前状态为Xi,visual表示其视野范围,其中移动步长为step,则可以通过下式计算第i条人工鱼的视野范围内选取下一个所在状态Xj
Xj=Xi+visual×rand()
(6)
如果相比于上一状态的解,状态Xj得到的解更优,那么就可以按照下式描述第i条人工鱼向该方向前进一步
(7)
如果相比于上一状态的解,状态Xj得到的解较差,则回到上一状态为Xi,对下一个所在状态Xj重新进行选取,在对设定的允许尝试次数进行设定后仍然无法得到最优的解,那么令第i条人工鱼进行随机行为[12]。
随机行为指的就是在视野范围内令第i条人工鱼向随机选择的一个状态移动
(8)
聚集行为指的就是在视野范围内使第i条人工鱼对领域范围内的其他人工鱼的数量nj进行搜寻,同时还要搜寻其中心的位置Xc,且Xc的解是Yc,这里将拥挤因子设定为δ,当满足Ycnf<δYi的条件时就说明该第i条人工鱼会向其他人工鱼的中心的位置Xc移动
(9)
鱼群的追尾行为指的就是在视野范围内第i条人工鱼会对具有最优解的人工鱼进行搜寻,当满足Ycnf<δYi的条件时就说明第i条人工鱼会移动向该伙伴Xj
(10)
人工鱼群,通过比较随机、追尾、聚群以及觅食等四种行为,其移动方法能够保证获得最优解,如果解满足最优解或者迭代次数满足设定值人工鱼群算法就会结束。
全局人工鱼群算法将全局最优信息引入到人工鱼的位置更新方法中,进而保证人工鱼群算法的全局搜索能力得到提升。在人工鱼进行觅食、聚群、追尾这三种行为的移动方向上加入全局最优信息Xbest_af,如第i条人工鱼选取向Xj方向移动是常规人工鱼群算法的表现形式,但是在全局人工鱼群算法中,该人工鱼的移动方向为Xj方向和全局最优位置Xjbest_af的合成向量,其具体的描述为

step×rand()
(11)
通过对这种全局人工鱼群算法进行应用就能够保证全局最优解获取的准确定和效率,避免在人工与更新位置时常规算法没有全局信息,避免局部信息造成精度低以及收敛速度慢等问题[13]。
4 光纤应变传感器网络布置优化实验研究
使用本文研究的光纤应变传感器网络布置优化方法进行薄钢板载荷响应实验的传感器优化研究,同时使用人工随机布置传感器的方式进行对比分析。该薄钢板由4个支撑点支撑,在钢板表面固定应变传感器。钢板尺寸为300 mm×300 mm×3 mm,钢板的密度为7 800 kg/m3,弹性模量为2.1×1011Pa,泊松比为0.3。实验系统简图如图2所示。薄钢板测试传感器布置平面图如图3所示。

图2 实验系统简图
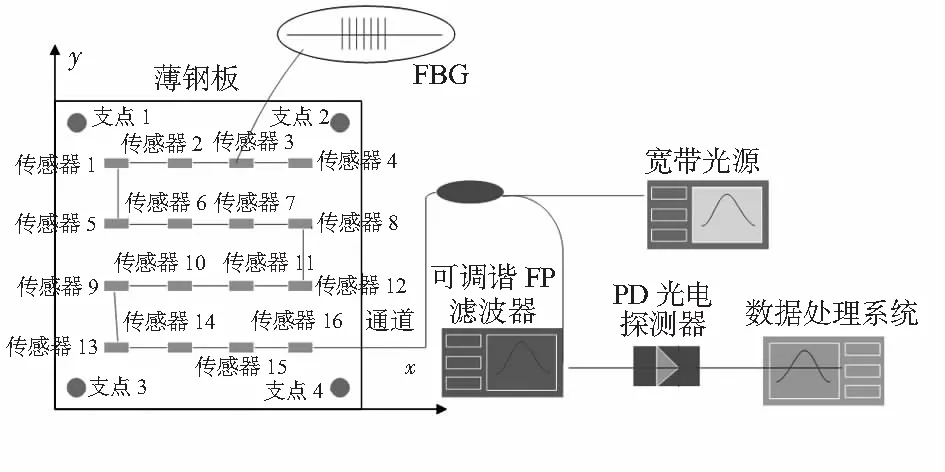
图3 薄钢板测试传感器布置
实验测得由人工随机布置传感器得到钢板的应变测量情况如图4所示,优化后布置传感器得钢板的应变测量情况如图5所示。

图4 人工随机布置传感器得钢板的应变

图5 优化后布置传感器得钢板的应变
对比薄钢板四角的实际应变以及光纤应变传感网络布置优化前后的结果如图6所示。

图6 薄钢板四角应变测试结果
将各个传感器节点测量误差平均值以图7形式表示。

图7 各个传感器节点测量误差平均值
光纤应变传感器网络布置优化实验研究表明:优化前,传感器测量应变误差最大值为28.08×10-6、最小值为14.92×10-6,平均误差为22.66×10-6。
使用本文研究的优化方法后,传感器测量应变误差最大值为8.72×10-6,最小值为2.54×10-6,平均误差为6.61×10-6。相比优化前分别降低了68.9 %,82.9 %和70.8 %。
5 结 论
1)本文针对光纤应变传感网络,使用人工鱼群算法进行传感器的节点布置优化研究。
2) 使用本文研究的优化方法后,使得测量的应变相比人工随机布置传感器测量值更接近真实值,具有较好的测量精度。
