基于相似日与EPSO LS-SVM的光伏发电功率预测*
2019-03-05龚尚红潘庭龙
龚尚红, 潘庭龙
(江南大学 物联网工程学院,江苏 无锡 214122)
0 引 言
光伏(photovoltaic,PV)发电受太阳辐射变化等天气因素的影响,发电功率表现出随机性、间歇性和不稳定性,并网时会造成对大电网系统的冲击[1]。因此,对光伏发电功率进行精确预测,是光伏发电并网后电网安全稳定运行的重要环节。目前,光伏发电功率预测在方法上主要包括物理方法以及统计方法。其中,物理方法过于依赖地理信息和气象天气预报,建模过程繁琐。统计方法是对光伏发电数据的输入输出统计规律建立预测模型,过程得以简化,目前运用较多。如文献[2]采用遗传算法优化反向传播(back propagation,BP)神经网络模型进行预测,但容易陷入局部最小,使问题得不到最优解。文献[3]通过模糊C均值聚类算法对原始样本进行聚类,生成模糊样本,再采用支持向量机(support vector machine,SVM)进行模型的训练,解决了样本小和维数高的问题,具有较强的泛化能力。最小二乘支持向量机(least square support vector machine,LS-SVM)[4]是标准SVM的扩展,采用二次规划法求解函数估计问题,使求解速度相对加快,泛化能力加强,在预测精度上也有所提高。
本文将对数据样本进行相似日选取,采用改进粒子群优化(particle swarm optimization,PSO)LS-SVM算法建模并预测,以实际光伏电站数据为例,验证模型的有效性。
1 相似日选取
1.1 光伏发电功率的影响因素分析
光伏阵列发电量受天气和地理等因素的影响,其输出功率[5]为
Ps=ηpvSI[1-0.005(T0+25)]
(1)
式中ηpv为光伏电池板的光电转换效率,%;S为光伏阵列总面积,m2;I为太阳辐照强度,kW/m2;T0为环境温度,℃。
一般情况下,光伏阵列的面积和光电转换效率可以认为是恒定的[6]。因此由式(1)可得出,太阳辐照强度和温度是影响光伏发电最重要的两个因素。
选取与预测日相似的数据样本作为训练集能有效提高预测精度,因此在预测前本文需要选取相似日。首先选取与预测日相同季节与天气类型的历史数据构成初步样本,然后将辐照强度数据和温度数据作为相似日判断的气象特征向量。考虑到光伏发电只在有辐照的时间段进行,故选取每天07∶00~18∶00时间段内12个整点时刻作为每日预测,因此第i日的气象特征向量为Yi,包括逐时辐照强度数据和温度数据的共24个元素,即
Yi=[yi1yi2…ym],m=1,2,…,24
(2)
1.2 相似日选取方法
本文采用加权灰色关联投影法进行相似日的评定,强调了关键影响因素,克服了灰色关联系数评价的劣势:
1)选取每天的辐照强度和温度作为气象特征,则历史日第i天特征向量如式(2)所示,式中,i=1,2,…n,n为历史样本;Yi前12个元素为辐照强度,后12个元素为温度,为了减少不同量纲对结论的影响,本文将气象特征向量数据进行归一化处理。
2)以待预测日的气象特征Y0为母序列,历史日第i天特征向量Yi为子序列,计算子母序列的关联值,建立灰色关联判断矩阵
(3)
可知,矩阵母序列所在第1行元素全为1,子序列任意值Fnm表示第n个样本中第m个因素所对应的关联值。
3)用CRITIC权重法[7]计算各个影响因素的权重
W=[w1w2…wm]
(4)
4)根据灰色关联矩阵F和权向量W计算加权灰色关联决策矩阵F′
(5)
5)计算各个历史日向量的加权灰色投影值Di。矩阵F′中第1行为待预测向量A0,后面各行对应历史日第i天的向量Ai。第i天历史向量的灰色关联投影值由Ai与A0向量间的夹角得出,计算Di
(6)
6)对比各个历史样加权本灰色关联投影值的大小,找出投影值较大的样本,作为训练预测模型的相似日样本集。
2 基于改进PSO算法的LS-SVM
在对光伏数据进行相似日的选取后,将建立基于LS-SVM的光伏功率发电预测模型。在LS-SVM算法中,有2个参数对算法功能表现有重要影响,即惩罚参数和核参数[8,9],本文提出采用改进的PSO算法对LS-SVM模型的参数进行优化。
2.1 进化粒子群算法
PSO算法[10]适用于非线性问题的优化,具有精度高、收敛快等优点。但其惯性权重和加速常数易早熟,且易陷入局部最优。
本文提出一种改进PSO算法,即融入线性递减权重和进化算法,并将其称为进化粒子群算法(evolution particle swarm optimization,EPSO)。首先,对权重进行线性递减,能有效避免早熟和后期振荡现象;其次,对权重和全局最优进行变异操作,改善算法的收敛性能。进化算法的进化机制来源于选种和突变,具有自适应、自组织、自学习特征,将其融入传统PSO中,能使优化效果更好,其过程如下:
1)粒子速度与位置更新遵循基本PSO的规律
(7)
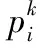
2)*代表该参数会通过突变而进化,其过程如下
(8)
式中wmax,wmin分别为惯性权重最大值与最小值;t为迭代次数;τ,τ′为学习因子,控制变异的幅度;N(0,1)为服从高斯分布的随机数。
2.2 EPSO-LSSVM的训练算法
本文用EPSO算法优化LS-SVM,能有效改善传统PSO和LS-SVM算法的不足,提高寻优的精度,有效平衡模型的复杂度与误差的精度。训练算法流程如图1所示。
适应度函数采用预测值与真实值间的平均相对误差
(9)

3 基于EPSO-LSSVM的光伏发电功率预测模型
3.1 设计预测模型
本文对不同天气条件下的发电功率进行预测,根据光伏发电特征,选取待预测日07∶00~18∶00时间段内12个整点时刻的数据用于建立模型。模型的输入变量为相似日气象数据与发电功率,其中气象数据包括太阳直接辐射、太阳漫辐射、温度、湿度、风速、风向;模型的输出变量为逐时发电功率值。建立模型后,根据天气预报给出的气象因素,对待预测日的功率进行预测。
3.2 参数设置
EPSO算法和PSO算法中进化迭代次数K=300,种群规模N=30。PSO中惯性权重w=0.8,学习因子c1=2,c2=2;EPSO中惯性权重最大值wmax=0.9,最小值wmin=0.9,学习因子τ=2,τ′=2。
4 算例分析
本文以国外某光伏电站2016年6月~2017年6月的实测发电功率数据和其对应的天气信息作为样本,选取电站2017年6月不同类型天气下12个整点时刻的发电功率进行预测,并将本文方法与SVM,LSSVM,PSO-LSSVM的预测结果进行对比。
在光伏电站2017年6月中,选取晴天、阴天和雨天3种典型的天气条件进行定性分析,其预测结果分别如图2。

图2 不同天气下预测结果
由图2(a)中,晴天时光伏电站的功率输出具有一定的规律性,3种预测结果都与实际功率比较接近,效果都较理想。
图2(b)中在实际测试时,阴天训练样本数较少,且天气情况复杂多变,云层频繁无规律运动对辐射影响大,气象因素会发生突变,影响对发电功率的预测。由图可知,3种方法的预测功率都能跟踪实际功率,但效果明显没有晴天条件下要好。在09∶00~12∶00和15∶00~16∶00时间段中,有突变发生,功率预测偏差较大,图中对比可知,在这些时间段中EPSO-LSSVM模型的预测曲线更接近实际曲线,能明显降低预测误差。
图2(c)中雨天辐照不强整体功率较低,电站有更多的随机性和不确定性,可以看出,EPSO-LSSVM模型的预测曲线更接近实际曲线,说明EPSO-LSSVM有更好的学习和映射能力。
本文选取了2个评价指标:平均绝对百分比误差(mean absolute percent error,MAPE)和希尔不等系数(Theil inequality coefficient,TIC)。其中,TIC为
(10)
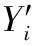
由表1可知,晴天时,太阳辐照较少受其他因素的影响,因此发电功率规律性强;而阴天和雨天为突变天气,辐照和温度等天气因素受云层和风速变化而变化,预测精度相对降低。对比4种预测模型误差可发现,3种天气条件下,EPSO-LSSVM模型的MAPE和TIC均最小,有着更优越的性能,表明EPSO-LSSVM模型在传统模型基础上,有更高的预测精度,更能适应随机性和波动性较大的天气类型。

表1 4种预测模型在不同天气条件下的误差估计
5 结束语
通过对光伏电站数据及相应天气因素相关性分析,提练影响光伏发电功率的主要因素(太阳辐射强度和温度)作为相似日的选取标准,使用加权灰色关联分析选取相似日,基于相似日用EPSO-LSSVM方法建立预测模型进行预测。从预测结果可以看出:相比传统预测模型,EPSO-LSSVM预测模型在不同的天气条件下都表现出更高的预测精度,以及更强的适应性,对光伏并网有较高的应用价值。
