基于SWD-AVDIF的齿轮箱复合故障诊断方法
2019-03-05程军圣黄祝庆卿宏军
李 娟,程军圣,黄祝庆,卿宏军,
(1.湖南大学 机械与运载工程学院,长沙 410082;2.常州湖南大学 机械装备研究院,江苏 常州 213100)
滚动轴承、齿轮作为齿轮箱的核心部分,其状态好坏直接影响整个设备的运行[1]。目前,国内外学者对齿轮箱诊断方法已经进行了大量研究,这些研究大多是基于齿轮箱某一部件的单一故障而展开,但齿轮箱中复合故障更为常见[2],其故障多表现为强度分布不均且相互叠加、彼此干扰[3],增加了故障诊断难度。因此,研究新的齿轮箱复合故障诊断方法具有重要的现实意义。复合故障信号主要包含啮合频率被转频调制的调制型齿轮故障信号和以轴承故障频率及其倍频为周期的脉冲型轴承故障信号[4]。传统的复合故障诊断方法以频带划分为基础,将故障信号分解到不同频带,进而提取故障特征进行故障诊断。经验模态分解(Empirical Mode Decomposition,简称EMD)具有类似二进滤波器组的特性[5],将振动信号分解成若干个不同频段且瞬时频率具有物理意义的固有模态函数(Intrinsic Mode Function,简称IMF)之和,并在故障诊断中得到了广泛应用[6]。但是,EMD分解高频分量带宽较大,频率分辨率低,在分解频率成分较为接近的复合故障信号时容易造成模态混叠[7],影响诊断的准确性。
文献[8]提出了一种基于群体智能算法的非线性滤波器——HS滤波(Hunting Swarm Filter,简称HSF),相比传统中值滤波器,HS滤波器具有更好的抗噪性。文献[9]对HS滤波器进行改进提出群滤波(Swarm Filter,简称SwF),在此基础上,提出了一种新的信号处理方法——群分解(Swarm Decomposition,简称SWD),并成功的将该方法运用到非线性、非平稳信号处理中。SWD借鉴EMD迭代滤波的思想,经迭代SwF滤波将原始信号自适应的分解为若干单一模态的振荡分量(Oscillatory Components,简称OCs)。SwF滤波器相当于一个带通滤波器,通过设计SwF参数可以控制OC分量主模态频率,使得SWD分解在模态分离方面,可以将频率相近的两个谐波信号分离,相比EMD具有更高的频率区分能力。本文将SWD方法引入故障诊断领域,用于分解齿轮箱复合故障振动信号。
SWD方法能够将故障信号分解到不同频率范围的OC分量中,但是无法从OC分量中直接读取故障信息,因此需要对OC分量进行解调分析。常见的解调方法有包络解调、广义检波滤波等[10],但包络解调两端会产生调制现象,致使解调误差增大;广义检波滤波则出现混频现象,在频率准确值的提取方面效果不尽人意。形态学解调是一种基于数学形态学的方法,通过设计具有滤波窗作用的结构元素对信号进行边缘匹配和处理[11]。平均差值形态算子(Average Difference Filter,简称 AVDIF)[12]作为一种基于形态学解调的新型组合差值算子,在抑制随机噪声和突出冲击信号上有很好的效果,对OC分量进行AVDIF解调能够降低带内噪声干扰、增强故障特征,相比前两种解调算法具有更高的准确性和精度。
基于上述分析,本文对比分析EMD与SWD方法的频率区分能力并提出一种基于群分解和平均差值形态算子(Swarm Decomposition-Average Difference Filter,简称 SWD-AVDIF)的齿轮箱复合故障诊断方法。该方法首先对齿轮箱复合故障振动信号进行分解;然后采用平均差值形态算子对分量信号进行解调;最后根据解调结果判别故障类型。齿轮箱复合故障仿真信号和实验信号验证了本文所提方法的优越性。
1 群分解方法
1.1 SWD分解
SWD通过迭代SwF滤波[9],将输入信号分解为多个OC分量之和。分解过程如下:
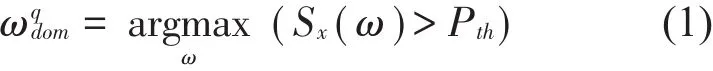
其中:sx(ω)表示韦尔奇功率谱[13],q表示该频率在SWD分解过程中第q次作为中心频率,Pth为阈值;
2)对输入信号x[n]进行SwF滤波[9],得到输出信号y[n],计算输出信号与输入信号的方差值StD值

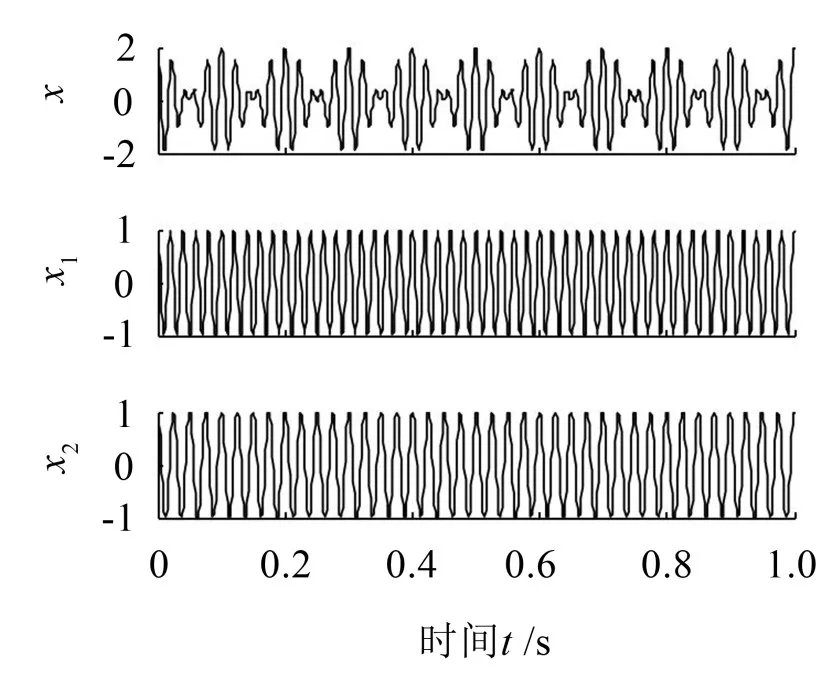
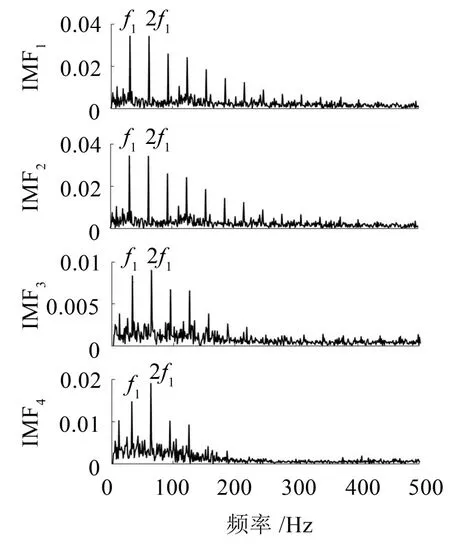
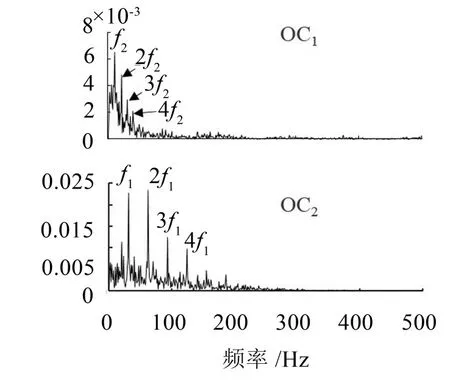
当StD>StDth时,以y[n]为输入信号重复SwF滤波,直到StD 3)更新输入信号 其中:R.,.(τ)为互相关函数(-(L-1)≤τ≤(L-1)),τ为时延。 4)利用新的“输入”信号,重复步骤(1)-(3)直到Sx(ω)≤Pth,∀ω,此时的输入信号为余量r[n]; 5)计算OC分量 考察下式所示仿真信号,采样频率为1 024Hz,采样时间为1 s 两个余弦分量频率比f2/f1=40/50=0.8,仿真信号及其时域波形图如图1。 图1 仿真信号时域波形 分别用EMD与SWD方法对仿真信号进行分解,为减小端点效应对结果的影响,采用互相关匹配端点延拓[14]对SWD的端点效应进行处理,分解结果如图2,分别求其有效分量的Hilbert时频谱如图3。 图2 EMD和SWD分解结果 图3 原始信号及两种分解结果的Hilbert谱 从结果可以看出,EMD在分解时将频率相接近的两个成份看成是一个调幅调频信号分解到同一个IMF分量中,得到的IMF1和IMF2时域波形呈现调幅特性,其Hilbert时频谱不能反映原始信号的瞬时幅值和瞬时频率,由此可以看出EMD不能分解频率接近的谐波信号。而SWD可以有效地对原始信号进行分解,并得到各个频率成分的OC分量,其中分量1和分量2分别对应OC1和OC2,其Hilbert时频谱和原始信号基本一致。 为进一步分析频率比对SWD分解结果的影响,利用式(5)构造一组等幅谐波信号,频率比范围满足:f2/f1∈[0.1,0.9]。首先对其进行SWD和EMD分解,然后利用Hilbert变换得到其平均幅值和频率,对结果进行归一化处理,得到归一化幅值和归一化频率与频率比的关系如图4。 图4 EMD和SWD频率区分能力 从图中可以看出当频率f2与f1相差较大,即f2/f1<0.5时,EMD可以有效的将原始信号分离开,得到的分量频率和幅值具有较高的准确性,但随着频率比的增大,在0.5 复合故障信号多表现为强度分布不均,直接对振动信号进行特征提取存在弱故障被强故障和噪声掩盖的问题,鉴于SWD方法提取谐波分量的优越性和AVDIF在强化冲击信号的作用,提出基于SWDAVDIF的旋转机械复合故障诊断方法。利用SWD将复合故障信号分解到不同频段的OC分量中,对OC分量进行AVDIF算子解调提取故障信息,通过其滤除带内噪声、强化冲击达到增强故障特征的作用。SWD-AVDIF方法具体步骤如下: 首先,通过SWD分解得到OC分量; 然后,对得到的OC分量进行AVDIF算子变换解调,即 其中:g(n)表示结构元素,Θ、⊕、∘、·分别表示形态学滤波的腐蚀运算、膨胀运算、开运算和闭运算四种基本运算; 最后,对解调后的OC分量进行频谱分析,得到多个SWD-AVDIF谱,提取故障特征。 为验证论文所提出方法的有效性,利用仿真信号进行分析。齿轮和滚动轴承是齿轮箱中最为重要的两个零件,因此,本文选取齿轮故障仿真信号和滚动轴承故障仿真信号来模拟复合故障信号,齿轮和滚动轴承的故障仿真信号如下 其中:A为齿轮故障幅值;fr为齿轮调制频率;fz为载波频率;M为轴承冲击个数;Bm为第m个冲击信号幅值,β为衰减系数;fn为共振频率;Tp为模拟冲击间隔;u(t)为单位阶跃信号。仿真信号采样频率fs:8 192 Hz,采样点数:8 192,并加入高斯随机噪声。仿真信号各参数如表1。 表1 故障仿真信号参数 故障信号及其分量如图5。 图5 复合故障仿真信号及其分量复合 齿轮故障特征频率为fr,滚动轴承故障特征频率fc=1/TP运用SWD-AVDIF方法对模拟复合信号进行处理,得到仿真信号SWD-AVDIF谱如图6。 图中看出,该方法能够将齿轮和滚动轴承故障分解到不同分量,在相应的故障频率及其倍频处能看到明显的谱线。证明了本文所提方法的有效性。 图6 复合故障仿真信号SWD-AVDIF谱 为了验证本文所提出的方法在工程实践中的实用性,以湖南大学齿轮箱复合故障振动信号数据为例验证该方法的应用效果。齿轮箱试验台为单级传动,如图7所示。 图7 齿轮箱故障实验台 通过激光切割的方式在齿轮和轴承上设置局部故障,其中滚动轴承的型号为SKF6307-2RS,在轴承的外圈上切割宽0.15 mm,深0.2 mm的槽来模拟轴承外圈故障;齿轮的齿数为37,在齿轮上切掉一个齿来模拟断齿故障。轴承和齿轮故障示意图如图8所示。 图8 故障齿轮和轴承 实验采样频率为8 192 Hz,采样时间为1 s。采集到如图9所示的故障信号。 图9 故障信号时域波形图 对其进行包络谱分析,得到其频率在0到500 Hz之间的包络谱如图10,从图中可以看出,轴承外圈的故障频率及其倍频在包络谱中表现明显,但是齿轮故障特征频率被掩盖,无法判断是否发生齿轮故障。 图10 故障信号包络谱 为了对比分析本文提出的方法,分别运用基于EMD-AVDIF、基于SWD分解的包络解调法和本文提出的方法对振动信号进行分析。其EMD分解得到7个IMF分量和余量,选取前4个分量进行AVDIF解调得到EMD-AVDIF谱,如图11。 图11 IMF1~IMF4分量EMD-AVDIF谱 从图中看出,在轴承故障频率及其倍频处存在明显谱线,但齿轮故障频率仍然被掩盖,无法判断是否发生齿轮故障,说明EMD-AVDIF不能实现复合故障诊断。 接着运用基于SWD分解的包络解调法和本文提出的方法对振动信号进行分解,选取幅值为0的直线型AVDIF解调算子,运用能量特征比[15]确定AVDIF算子结构元素尺寸为31。将故障信号进行SWD分解,得到的OC分量如图12。 图12 复合故障信号OC分量 对前两个分量分别进行包络解调和AVDIF解调得到SWD-包络谱和SWD-AVDIF谱,如图13、图14。 图13 SWD-包络谱 图14 SWD-AVDIF谱 由两种频谱图可以看出SWD可以实现复合故障信号分解,但相比SWD-包络谱,本文所述方法在解调时加强了冲击信号并削弱了随机噪声的干扰,得到的SWD-AVDIF谱降低了高频处噪声谱线的干扰,加强了低频部分故障特征。综上,充分说明了相比EMD-AVDIF法和SWD-包络法,本文所提出的方法更适合用来进行齿轮箱复合故障诊断。 针对旋转机械复合故障诊断方法的不足,提出了一种基于SWD-AVDIF的齿轮箱复合故障诊断方法。 (1)与EMD对比,分析了SWD方法在频率区分能力上的优越性,SWD在分解不同频率的等幅周期信号时,分解能力受频率比f影响较小,能够有效分离频率相接近的谐波分量; (2)将SWD方法引入齿轮箱故障诊断领域,提出了SWD-AVDIF方法; (3)运用SWD-AVDIF对齿轮箱复合故障振动信号进行分析,仿真信号和实验信号结果表明该方法能够提取复合故障中的微弱信号,提高了故障诊断的准确性。

1.2 SWD频率区分能力研究
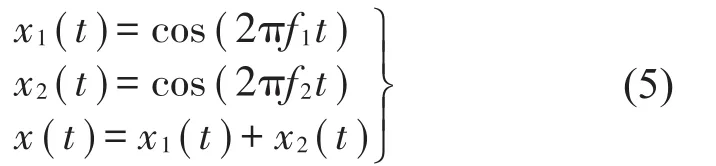



2 SWD-AVDIF方法
2.1 SWD-AVDIF算法

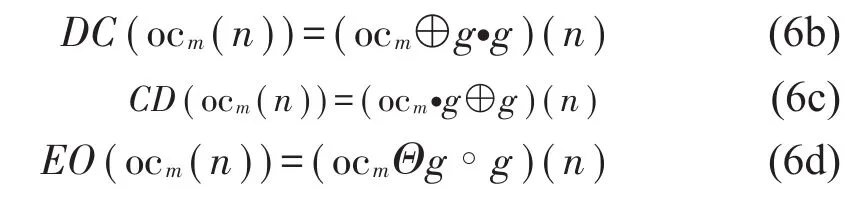
2.2 齿轮箱复合故障仿真分析




3 齿轮箱复合故障实验信号分析






4 结语
