汽车悬架衬套静动特性分析中缩径量影响研究

2019-03-05代正莉付江华陈哲明许言明

噪声与振动控制 2019年1期

陈宝，代正莉，付江华，陈哲明，许言明

（1.重庆理工大学车辆工程学院，重庆 400054；2.河北华密橡胶有限责任公司，河北邢台 054000）

车用橡胶衬套通常由多种材料（如金属、塑料等）组合硫化而成，通过调整材料配方可使同形状衬套得到不同的静、动态特性；车用防振橡胶部件主要应用在整车动力、传动、转向、排气、悬架等系统中[1-3]。橡胶衬套的基本作用是衰减振动，其相应高阻尼特性能将车轮与路面产生的激励迅速衰减，减少通过底盘传递到车身的振动，保证整车的行驶平顺性。在橡胶衬套特性研究的工作中，橡胶衬套特性的分析要比对金属元件的分析复杂得多。金属的力学性能只需要较少的几个参数（如弹性模量和泊松比）来表征，而橡胶的材料特性和几何特性都呈非线性，因此，在早期的橡胶产品开发中，大多采修正的方法[4]。但该方法成本高、时间用反复试验长，精度低。

对于橡胶件特性的研究，国内外汽车相关研发制造部门一直将其视为汽车关键零部件研究中的难重点。王文涛[5]研究了Mooney-Rivlin模型、Yeoh模型及3阶Ogden模型计算橡胶悬置刚度的适用范围，结果表明，较小应变和中等应变状况下3种模型的计算值与实测值均具有较好的一致性；在较大变形情况下（最大应变大于1）3阶Ogden模型具有相对较为稳定的预测精度。同年，刘万里[6]对某车用橡胶悬置进行了应力松弛试验，在ABAQUS中获得了橡胶材料拟合应力松弛系数，建立了橡胶的超-黏弹性材料模型，对该悬置的静动刚度、阻尼特性进行了仿真分析，并进行了试验验证。胡启国[7]采用显式有限元计算方法对大型矿车的发动机橡胶悬置进行了静、动态刚度特性分析，并在试验台上进行试验来检测数值仿真的精度，得到了理想的仿真精度。

综上所述，以往橡胶衬套的研究中考虑缩径量对其静动特性的影响并不多。橡胶衬套在实际应用中都通过硫化与刚性部分过盈配合，其过盈量（即缩径量）大小对静动特性乃至隔振效果、整车平顺性都有重要影响。所以本文以某汽车悬架橡胶衬套为研究对象，通过改变其缩径量大小对其静、动特性进行了研究，并结合试验验证仿真的正确性，结果显示橡胶衬套静、动刚度随缩径量的增加而增大，当缩径量小于0.6 mm时静、动刚度与缩径量呈近似线性关系；当缩径量大于0.6 mm后静、动刚度随缩径量增大而增大的速率急剧变大。研究表明仿真模拟衬套静动特性的方法可行，能指导类似结构特性研究并为考虑衬套影响的整车性能研究提供快速、准确的参数属性支撑。

1 有限元模型

橡胶衬套如图1所示，橡胶胶体与内外金属刚性圈都是通过硫化的方式相连安装在车身上。橡胶衬套承受外力作用时，橡胶材料呈现几何和边界双重非线性特征。大位移或大应变问题是指几何非线性，对于变形过大的物体，不可忽视变形量导致的非线性平衡方程；另外，边界条件可引起边界非线性即接触非线性；同时，橡胶材料本身也是非线性的，当需要开展橡胶衬套有关分析时，应将3种非线性特征一起综合考虑。

图1 某汽车橡胶衬套

对该橡胶衬套模型进行网格划分时，可以简化部分结构，采用六面体单元（C3D8H），衬套中心孔处的内刚性圈使用二维的Shell4单元来模拟；衬套在结构静刚度试验时通常将外刚性圈完全固定，同时外刚性圈与金属内刚性圈都采用硫化方式与橡胶体连接，有限元建模时选择金属内刚性圈与橡胶节点公用，而外刚性圈因与车架为过盈配合，通过对橡胶外表面上的节点施加强迫位移来实[8]。有限元模型如图2所示。

图2 橡胶衬套有限元模型

2 材料参数

橡胶材料被认为是一种典型的各向同性且不可压缩的超弹性材料，在确定橡胶材料的本构关系时，其材料参数是由试验数据和理论计算公式进行最小二乘拟合得到。除此之外，橡胶衬套受到动态载荷作用时，除了表现超弹性特征外，还具有黏性特征，所以在对橡胶衬套进行动态特性研究时还应建立橡胶材料的黏弹性本构模型。

本文是通过单、双轴向拉伸和平面剪切3种类型试验对橡胶材料参数进行拟合得到3阶Ogden模型材料参数，Ogden模型应变能是以λ1，λ2，λ33个主伸长率为变量。其应变能密度形式为：

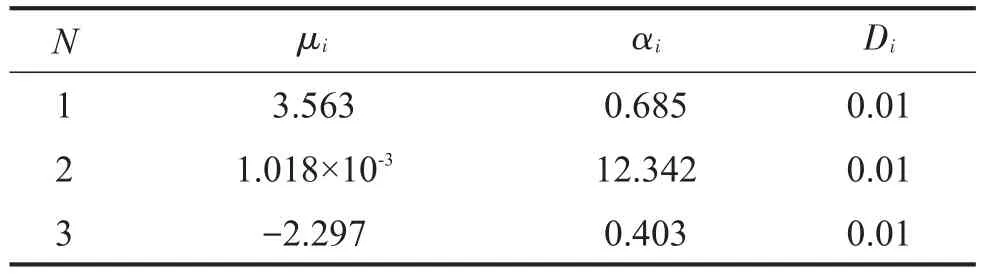
表1 3阶Ogden模型材料参数

黏弹性本构关系建立为3阶PRONY级数，对于橡胶类超弹性材料当不考虑温度影响时松弛过程中剪切应力τ(t)可表示为时间的卷积。

式中：G0是初始剪切模量；g(t)=G(t)/G0是无量纲。将G(t)用PRONY级数展开得

式中：gi、τi为与材料相关的常数。橡胶材料黏弹性参数如表2所示[9]。除橡胶之外，钢材密度为ρ=7 850 kg/m3，E=210 000 MPa，μ=0.3。

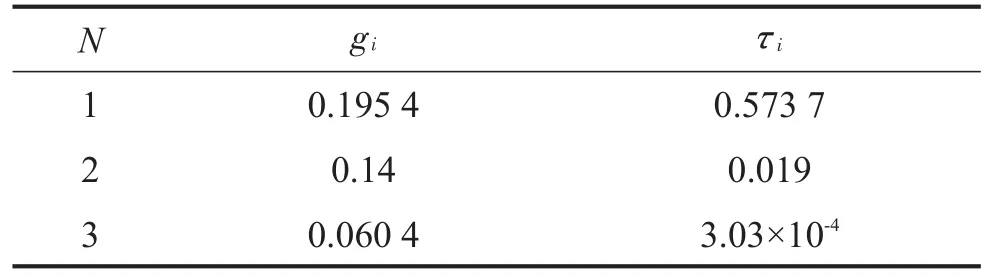
表2 3阶PRONY级数系数

3 静、动刚度仿真

采用ABAQUS/Standard模块对橡胶衬套进行不同缩径量下静、动刚度仿真，具体缩径设置如表3所示。

表3 不同缩径量值/mm

在进行静刚度仿真时创建4个通用分析步，首先在初始分析步中固定衬套中心点6个自由度，并在第一个分析步中沿衬套径向设置不同缩径量，以预紧橡胶衬套；在第三分析步中固定衬套外圈节点6个自由度使外圈节点保持在压缩位置，最后在第四个分析步中释放中心点处径向自由度并加载径向载荷F=3 000 N。

对衬套进行动刚度仿真时创建3个通用分析步和一个隐式分析步，前3个通用分析步与静刚度仿真时相同，在最后一个隐式分析步中沿衬套径向施加位移正弦激励信号U0sin(ωt)，取位移激励信号的频率为15 Hz，幅值为0.5 mm。

4 橡胶衬套静、动刚度仿真结果

图3为0.2 mm、0.4 mm、0.6 mm缩径量下静刚度仿真得到的力与位移关系曲线，其斜率则为静刚度值。各缩径量下橡胶衬套静刚度值如表4所示。

图3 不同缩径下力与位移关系曲线

由表4可知橡胶衬套静刚度随缩径量增大而增大，静刚度值与缩径量大小接近线性关系，将缩径量与静刚度值进行线性拟合后得到静刚度与缩径量关系曲线如图4所示。

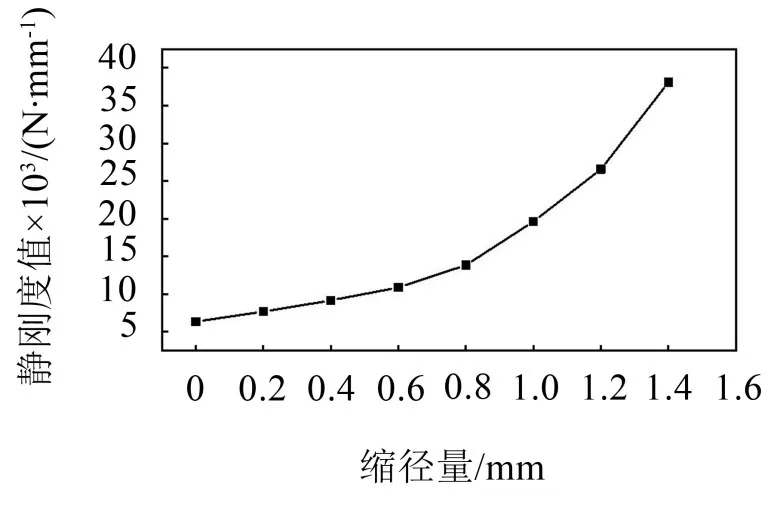
图4 静刚度与缩径量关系曲线

表4 各缩径量下静、动刚度仿真结果

如图5、图6和图7所示，分别为0.2 mm、0.4 mm、0.6 mm缩径量下动刚度仿真得到的力与位移之间的关系曲线，该曲线呈现环形圈是因为出现了动特性反应滞后现象。

图5 缩径量为0.2 mm时力与位移关系曲线

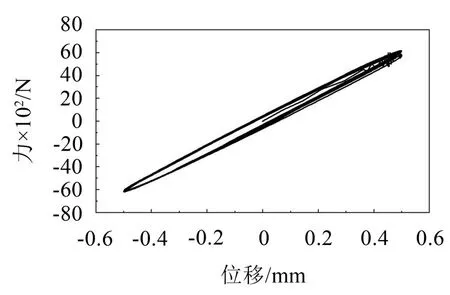
图6 缩径量0.4 mm时力与位移关系曲线

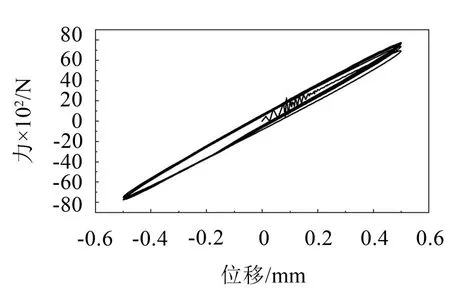
图7 缩径量0.6 mm时力与位移关系曲线

在计算动刚度时，取该迟滞曲线的中心线，对其进行拟合，然后取拟合直线的斜率计算动刚度，各缩径量下橡胶衬套动刚度值如表4所示。对各缩径量下动刚度值进行拟合的到动刚度值与缩径量大小的关系曲线如图8所示。

由图4、图8可知不管是静刚度还是动刚度均随缩径量的增大而变大，当缩径量小于0.6 mm时静、动刚度与缩径量呈近似线性关系；当缩径量大于0.6 mm后静、动刚度随缩径量增大而增大的速率急剧变大。

由表3可知随着缩径的增大橡胶衬套的动静比也略有增大，而动静比橡胶衬套静、动态刚度特性的一重要参数，动静比过大会降低橡胶衬套的寿命[10]，通常情况下，橡胶衬套应具有较小的动静刚度比，橡胶衬套动静比一般在1～2之间。

图8 动刚度与缩径量关系曲线

5 静、动刚度试验

为了验证仿真的准确性，对橡胶衬套静、动态刚度特性进行试验来检测，用于试验的橡胶衬套缩径量为0.2 mm。静刚度试验是通过如图9所示微机控制的MTS试验机测试所得，衬套通过专用夹具固定在试验机上，通过螺杆将安装在夹具中的衬套与U形叉固连以测量其静刚度。试验加载方式为径向加压，力从零随时间线性增加至设定值，加载力设定范围是0～3 000 N。试验过程是从零时刻起开始，试验机作动部的运行速度为1.0 mm/min，相应MTS试验机的微机控制系统自动记录每一时刻的载荷与衬套变形量的大小。

图9 MTS试验机

动态试验是利用一台如图10的U-CAN动态特性试验台，安装方式如图11所示。

图10 动态特性试验台

图11 橡胶衬套安装方式

动态载荷采用位移控制，振幅为0.5 mm频率为15 Hz的稳态正弦位移激励，采集得到橡胶衬套的位移与作用反力，通过计算得到该频率下的动刚度。

试验测试0.2 mm缩径量下橡胶衬套静刚度值为7 152 N/mm，动刚度值为9 369 N/mm。静刚度试验曲线与仿真曲线对比如图12所示，动刚度对比时为保证对比曲线清晰取动刚度仿真曲线中的一条与试验曲线对比如图13所示。

图12 0.2 mm缩径量下静刚度对比曲线

图13 0.2 mm缩径量下动刚度对比曲线

将测试得到的数据与仿真的数据进行对比，可知静刚度值相对误差为7.7%，说明以上有限元仿真结果比较准确；动刚度值相对误差为8.1%，相对与静刚度误差较大，这是因为动刚度仿真的准确度是基于对橡胶衬套本身固有频率的准确计算，要求对其橡胶材料的力学性能、质量等参数的准确性更高，以及橡胶衬套动态特性具有迟滞现象，在进行动刚度数据处理时出现误差也较大。总体来讲，该橡胶衬套静、动刚度仿真值与试验测试相对误差均在可接受范围以内，说明仿真具有一定的参考性。