GMR-1 3G卫星通信系统频率偏移估计算法*

李质彬，司伟立，韩 娟

（1.重庆邮电大学通信与信息工程学院，重庆 400065；2.北京中科晶上科技股份有限公司，北京 100180； 3.中国科学院计算技术研究所无线通信技术研究中心，北京 100190；4.中国科学院大学，北京 100049）

0 引 言

地面蜂窝通信系统近年来发展迅猛，用户对移动通信的需求也在日益增长。为了顺应这种需求，地面蜂窝通信系统的改进主要集中在现有制式的服务质量和5G研究上[1-3]。但在一些特殊时期或者地点，地面基站很难保障其通信服务。例如，海上、山区以及自然灾害地区，地面基站覆盖困难以及遭受到损坏时，卫星通信作为地面通信的补充和应急通信手段，其覆盖范围广、不受地理条件和通信距离限制等优势的价值得以体现[4]。GMR-1 3G系统空中接口保留了在卫星系统中成熟的TDMA/FDD体制[5]。作为新一代卫星移动通信系统空中接口技术规范，GMR-1 3G卫星通信系统在我国不断发展，产业链也逐步形成。

通信系统中，频偏估计与补偿的精度是数字接收机整体性能和正确解调的关键。频偏估计算法主要有数据辅助算法和无数据辅助算法，两者的区别在于是否在突发中加入已知的辅助数据。有数据辅助的频偏算法大多基于最大似然估计，其中的经典算法如Fitz算法[6]、Kay算法[7]、L&R算法[8]和M&M算法[9]等。无数据辅助频偏算法主要基于数据辅助算法的改进。文献[10]采用时域信号相关与相位旋转的方式去除QPSK信号的调制相位，再用Kay算法或者L&R算法进行频率偏移计算。当使用Kay算法时，估计范围较大但算法的噪声门限较高；使用L&R算法估计时，提高估计精度会降低估计范围。文献[11]通过Q次倍归一化信号进行自相关差分相位的加权求和得到频率偏移。文献[12]对M&M进行改进，提出了A&C算法，并使用A&C算法粗估计后用L&R算法精估计的方法实现了低信噪比时的大范围频偏估计，但是其两步法的估计方式时间复杂度较高。

针对目前无数据辅助频偏估计算法在低信噪比时无法兼顾估计范围和估计精度的问题，本文提出了一种新的频偏算法。该算法通过对π/4-CQPSK调制信号去累加调制相位差的方式去除调制相位，延时差分得到相位增量信息，再经过平滑处理和函数加权后线性拟合得出频偏。仿真结果表明，该算法在低信噪比的情况下保持了高估计精度，同时兼具较大估计范围，实用价值高。

1 频偏估计原理

假设接收信号进行了准确的信号同步，对于PSK调制信号，其模型可以表示为：

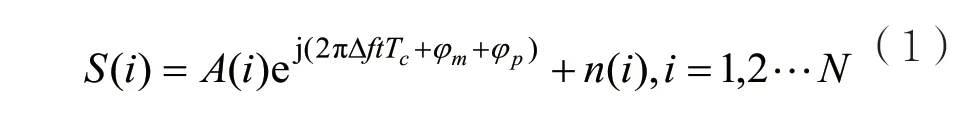
其中i为符号位置，A(i)表示复数幅度值，Tc为符号周期，Δf为频偏，φm为调制相位，φp为初始相偏，N为符号数。n(i)为复高斯白噪声序列，其实部与虚部皆均值为0，方差为σ2。首先，对S(i)取差分相位：

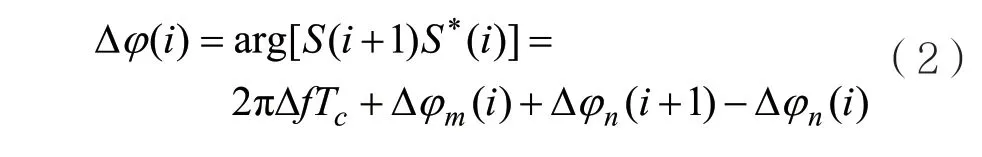
其中S*(i)表示S(i)的共轭，arg[·]表示取相位运算，幅角范围(-π,π]，φn(i)表示由n(i)引起的相位噪声，Δφm(i)表示两个符号调制相位差。对于PSK调制信号的无数据辅助频偏估计算法，采用M次方非线性变换[13]后，可以消除调制信息的影响。

定义目标函数为：

向 量Δφ=[Δφ(1),Δφ(2),…Δφ(i)]T，e=[1,1,…1]T，[·]T表示转置运算，C是Δφ(i)的协方差矩阵。根据Kay算法原理，当目标函数J取最小值时可以得出估计值Δf，其给出的解为：

Kay算法在信噪比较高时可以对大范围的频偏进行估计，但是噪声门限较高，在估计低信噪比信号频偏时估计精度较差。在对实际信号进行频偏估计时，频偏值往往要在低信噪比的信号中估计出来。为了在低信噪比时提高估计精度，现有的估计算法通常会降低估计范围。以Fitz为例，以下直接给出无数据辅助的Fitz算法频偏计算公式：

其中，待估计信号通过M次方去调制。R(m)表示延时m个符号的自相关函数，表达式为：

Fitz在低信噪比时可以通过提高延时值L获得高估计精度，此时估计范围会减小；减小L值增大估计范围，但会降低估计精度。实际使用Fitz算法进行频偏估计时，需要权衡估计精度和估计范围，选择合适的延时值L。或者采用两步法先粗估计大致频偏，对原信号补偿后再精估计得出精准估计值。以下Fitz算法与新算法进行对比试验，会根据对比的需要选择合适的延时值L，尽可能发挥Fitz算法某个单一方面的性能。

2 频偏估计新算法

考虑π/4-CQPSK信号调制特点，它实质是两个相位相差π/4的QPSK星座图交替调制。所以，直接采用常规的M次方去调制法时，需要M=8。较之QPSK调制频偏估计范围会小一半，且非线性变化会放大噪声的影响[13-15]，提高算法的噪声门限。另外，在自相关运算时，延时奇数个符号与延时偶数个符号，自相关会有π/4相位差，因此直接使用高时延自相关运算的频偏算法在用于π/4-CQPSK调制信号时较为困难。

新算法信号采用式（1）的信号模型，对其前后符号共轭复乘，得：

其中Δφm(i)为前后符号调制相位差。π/4-CQPSK调制方式时，它的取值为

对式（7）取相位，有：

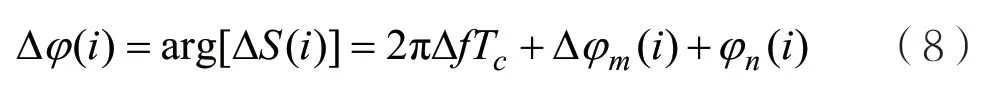
不考虑噪声φn(i)的影响，同时假设由频偏Δf引起的相偏时，可通过对相位差Δφ(i)直接判决得到实际调制相位差Δφ´m(i)，判决方式 如下：

只考虑符号S(i)的调制相位，可以看作是符号S(i-1)的调制相位和两符号调制相位差之和。通过递推可知，当前符号的调制相位可以看作是第一个符号的调制相位与当前符号之前所有前后符号调制相位差的和。那么，各符号的调制相位可以通过去除累加调制相位的方式去除：

其中Δφ´m(0)为符号S(1)取相位后通过式（9）判决所得。通过上述方法，可在不增大噪声影响的情况下去除调制相位。这里重写去除调制相位后的各符号相位：

由式（11）可知，相位φ´(i)中包含频偏相位，同时还残留着相偏和噪声相位。频偏相位与符号位置i呈线性关系。为了去除相偏的同时平滑噪声的影响，定义相位增量R(m)为：

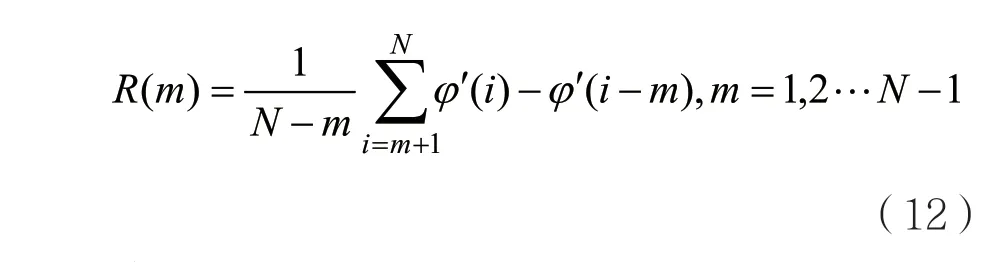
其中：

R(m)中相位由频偏相位和噪声两项组成。其中，频偏相位与延时值m呈线性关系；噪声项为0均值的加性高斯白噪声，对于所有m值的R(m)都是同分布的。可知，低m值时，式（12）中相位增量φ´(i)-φ´(i-m)噪声项的影响较大，但由于R(m)累加的数据较多，取平均后可以平滑噪声项的影响。随着m值的增大，累加数据减少，但高时延的R(m)中Δf与m的乘性关系增强了频偏相位项，使其具有了更好的抗噪性能。此时，频偏估计实际上是在混入噪声后的相位增量R(m)中估计出Δf。不考虑噪声影响，R(m)与m满足R(m)=km+b，其中k=2πΔf Tc。因此，利用线性拟合就可得到频偏估计值。

在进行线性拟合前，还需要对不同m值的相位增量R(m)加以不同的权值，以进一步减小低m值噪声项带来的相位误差和高m值累加数据少、随机性大对估计精度的影响。

令：

根据线性拟合公式得出频偏值Δf为：

3 仿真验证

3.1 估计均值与估计范围比较

仿真数据符号速率fs=16 kSps，采样速率fs×480，滤波器滚降系数0.35，同步后取最佳采样一路数据，仿真数据取长度N=40。对比算法有本文所述算法NEW和采用M次方去调制相位的Fitz算法（M=8）。无数据辅助时，仿真结果如图1所示。其中，图1对比有噪声和无噪声时NEW算法的估计范围。图2对两种算法的估计范围进行比较，SNR为0 dB。

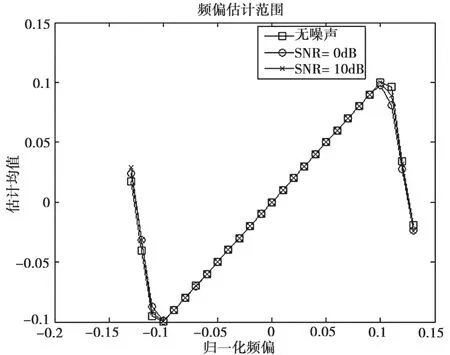
图1 噪声对估计范围的影响

由图1可以看出，在SNR=0 dB和无噪声时，估计范围基本一致，且噪声对估计范围的影响不大，其归一化估计范围为±0.1。图2比较了不同L值Fitz算法与新算法的估计范围，由于Fitz算法不同的L值会影响算法的估计范围，为了尽可能表现Fitz算法的估计范围，在M次方去调制后采用L=1和L=2的Fitz算法进行仿真。根据仿真结果可以得出，新算法的估计范围大于M次方去调制的Fitz算法。

图2 各算法频偏估计范围比较

3.2 均方误差对比

均方误差可以衡量算法的精度。仿真数据长度N=40，加以归一化频偏Δf=0.001，对比算法为不同L值的Fitz算法，均方误差值由每个SNR值测试 3 000次计算。仿真结果如图3所示。

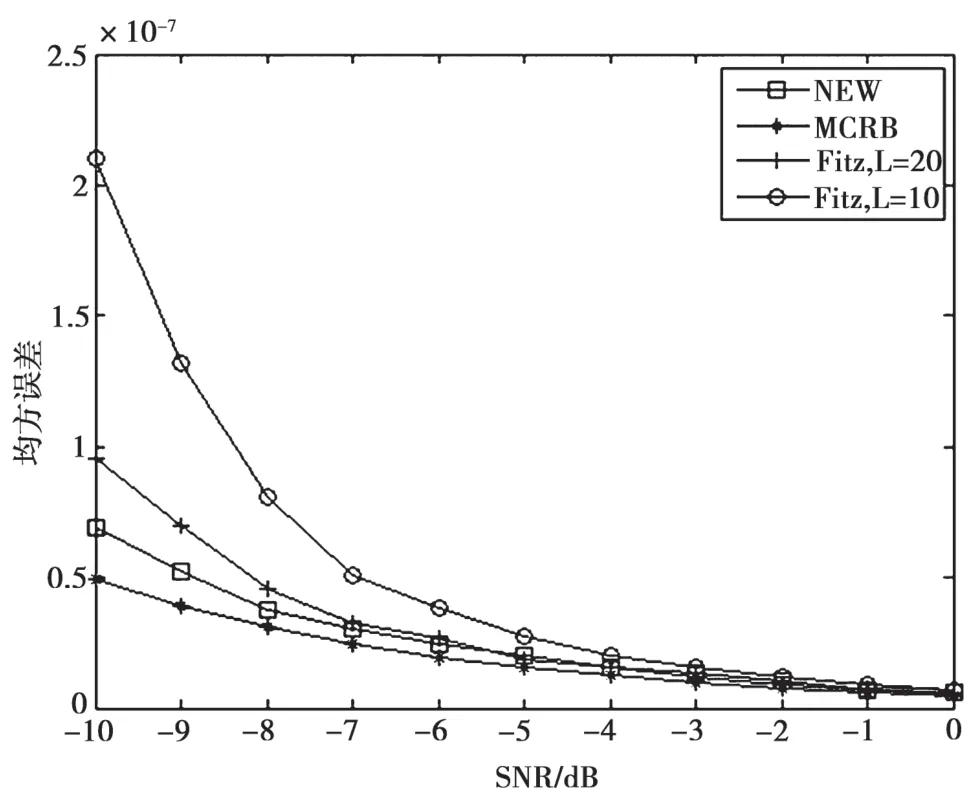
图3 均方误差

Fitz算法L值越大，其估计精度越精确。对比试验采用的Fitz算法L=N/2和L=N/4，即L=20和L=10。由图3可以看出，低信噪比时，新算法估计精度要优于Fitz算法；随着信噪比的提高，两种算法性能逐渐接近，SNR=-5 dB时，L=N/2的Fitz算法与新算法估计精度基本一致；在SNR=0 dB时，两种算法都逼近克拉美罗界。

令SNR=0 dB，Δf T=[-0.15,0.15]，对比不同L值Fitz算法和新算法的频偏与均方误差的关系，结果如图4所示。

图4 归一化频偏与均方误差

可以看出，新算法均方误差在估计范围内估计性能无明显变化，且会优于Fitz算法；Fitz算法随着L值的增加估计精度提升，估计范围下降；三种算法在频偏超出估计范围后，估计值迅速偏离理想值。

4 结 语

本文研究了GMR-1 3G卫星通信系统的频偏估计问题，针对π/4-CQPSK调制信号的特点，提出了一种基于各符号累加调制相位差去调制相位的方法，保留了各符号频偏引起的相位与噪声相位之间的关系。与传统M次方去调制的方法不同，该方法不引入非线性变化，所以不会放大噪声的影响。通过延时作差得到相位增量信息，根据频偏相位与噪声相位的关系，采取平滑处理和函数加权的方法抑制噪声的影响，最后进行线性拟合得到频偏估计值。新算法具有高估计精度，同时兼具较大的估计范围。经过仿真试验对比，新算法在估计精度和估计范围上都优于M次方去调制的Fitz算法，可以完成GMR-1 3G系统的频偏估计，具有较高的使用价值。