基于反向传播神经网络的自适应SCL译码算法*

义 炫，刘爱军

（陆军工程大学，江苏 南京 210007）

0 引 言

当N→∞，Polar在SC译码算法下的性能可以达到香农极限[1]，但是对于短码和中长码，其译码性能将下降很快，其性能比已提出的Turbo码和LDPC码性能差很多。因此，为了解决这一问题，SCL译码算法被提出[2]。不像SC译码器只保留一条译码路径，SCL译码器同时保留L条译码路径，其复杂度相应的也为SC译码器的L倍，为O(NlogN)。当列表大小L很大时，SCL译码器的性能已经超过了Turbo码和LDPC码等码字。然而，较大的列表大小也导致了较高的译码复杂度和译码延时，从而限制了SCL译码在实际中的广泛运用。为了解决这个问题，许多自适应SCL译码方案被提出[3-4]。

文献[3]提出了一种上升模式的自适应的SCL译码器，通过不断扩大L值，直至L条路径中有能通过CRC校验的路径才停止译码。这种上升模式的SCL译码器能够在同样的性能下有效减小计算复杂度，同样复杂度的情况下有效地提升了性能。但是，这种上升模式的自适应SCL译码器控制逻辑过于复杂，且每一帧重复译码次数不固定，导致译码延时也不可控。相比于上升模式的自适应SCL译码器，文献[4]提出了一种下降模式的自适应SCL译码器，根据路径特性差值特征来适当缩减列表大小L。该方法在牺牲较小的性能情况下有效地减小了复杂度，但是在中高信噪比下，复杂度减少并不可观。

反向传播神经网络是1986年由Rumelharth和McClelland为首的研究者提出。反向传播神经网络是一种基于误差反向传播算法的多层前馈神经网络。通过反向传播学习算法，不断调整神经元之间连接的权值，使得神经网络的实际输出值与期望输出值的误差均方差逐渐降至最小，因此可以从输入中得到任何非线性映射关系输出[5-7]。目前，在人工神经网络的实际应用中，反向传播神经网络是应用最广泛的一种神经网络模型。它主要应用于函数逼近、模式识别、分类器和数据压缩四个方面。因此，可以利用反向传播神经网络预测每一帧Polar码码字所受到的信道干扰程度，自适应地选择列表大小，从而进行自适应的SCL译码。

本文充分利用了Polar码码字的结构特性——冻结位。冻结位作为收发双方都已知的数据，和信息位一样，受到信道噪声的干扰。它的软信息同样可以反映出信道条件。因此，首先通过人造信号和干扰，通过软件仿真得到相关的冻结位信息作为反向传播神经网络的训练数据。其次，利用所得训练数据训练反向传播神经网络，以致能够准确预测每一帧Polar码码字所经过的AWGN信道的信噪比等级。根据事先设定的信噪比等级与列表大小的映射关系，自适应地调整列表大小，从而自适应地进行SCL译码。结果表明，所提出的方案能够在保证SCL译码器性能的情况下，有效地降低SCL译码算法的计算复杂度。

1 反向传播神经网络

1.1 拓扑结构

反向传播神经网络是一种多层前馈网络，由输入层、输出层和隐含层三种层次结构的完全连接形成，其中可以包含多层隐含层。图1所示的是一个三层的反向传播神经网络，即只包含一层隐含层。在反向传播神经网络中，输入层包含n个输入层节点p1,p2,…,pn，隐含层包含k个隐含层节点z1,z2,…,zk， 输出层包含m个输出层节点q1,q2,…,qm。其中，n、k、m为任意的正整数。输入层节点pi与隐含层节点zj之间的连接权值为wij，隐含层节点zi与输出层节点qj之间的连接权值为vij。

图1 三层神经网络的拓扑结构

反向传播神经网络包括信号的前向传播过程和误差的反向传播过程。在信号的前向传播过程中，输入信号自输入层节点输入，经隐含层节点的非线性变换，最后到达输出层节点产生输出信号。如果实际的输出信号与期望的输出信号有所差别，它们之间的误差将逐层反传，并各层节点与节点之间所有连接的权值根据反传的误差根据一定算法进行调整，通过修改各个节点之间连接的权值，使得实际的输出信号逐渐逼近期望的输出信号，这就是误差的反向传播过程。当有多层隐含层时，每一层节点的状态仅仅影响下一层节点的状态。隐含层的所有节点与外界没有直接的联系，但其任何一个节点状态的改变都会影响到输入与输出的关系。

1.2 反向传播算法

所有的神经网络在接受训练时，不断将输出信号与理想信号相比较，并按学习算法改变权值，直到网络的输出信号对所有训练样本与理想输出信号之差在要求的误差范围之内。与大多数学习算法类似，反向传播算法能够使得反向传播神经网络产生尽可能逼近理想的反应。在经过反向传播神经网络信号前向传播过程后，实际的输出信号与期望的输出信号的偏差反向传播。在大多数反向传播神经网络中，用误差平方和描述实际输出信号与期望输出信号之间的偏差。反向传播神经网络通过负梯度下降算法，利用迭代运算，反复调整和训练网络的权值，使得输出信号与期望信号尽可能接近。

以如图1的三层神经网络为例。在输入为P=(p1,p2,…,pn)时，假设所期待的理想输出和网络的实际输出分别为T=(t1,t2,…,tm)和Q=(q1,q2,…,qm)，那么反向传播算法的描述如下。

（1）定义一个损失函数：

（2）计算隐含层到输出层的连接权值vij的 梯度：

其 中，δ1i=(ti-zi)f´(N1i)，N1i=∑vijqj-θ1i，θ1i是隐含层到输出层的一个阈值函数，f´(·)是激活函数的反函数。在神经网络中，阈值函数是指神经元节点接受到的刺激大于这个阈值时才会触发该神经元节点去影响下一个神经元节点的刺激动作。如果小于这个阈值，该神经元的刺激就不会刺激到下一个神经元。激活函数则是用来加入非线性因素的，通常有Sigmoid函数、tanh函数、ReLU函数和Softmax函数等。本方案中，采用tanh函数，表达式为，具有零均值和收敛速度更快的优点。

（3）计算隐含层到输出层的连接权值wij的 梯度：

其中，δ2i=f´(N2i)∑δ1ivij，N2i=∑wijpj-θ2i，θ2i是输入层到隐含层的一个阈值函数，f´(·)是激活函数的反函数。

（4）更新权值wij和vij：

其中，

η、η´是学习速率，反映了反向传播过程中梯度下降的步长。

（5）更新阈值θ1i和θ2i：

从反向传播算法的过程可以看出，它的主要思想是利用正向传播后实际输出与期望输出的误差来估计输出层前一层的误差，再用这一层误差估计更前一层的误差，如此获取各个层的误差估计，进而利用这个误差估计更新各层之间的连接权值和阈值，并利用更新后的权值和阈值重新计算输出误差，直至输出误差达到符合的要求或者已经达到了最大迭代次数。

2 自适应SCL译码算法

本节主要介绍基于反向传播神经网络的自适应SCL译码器方案。方案中通过训练好的反向传播神经网络来预测每一帧所受到的干扰程度的大小，并用信噪比等级衡量这个干扰的大小。根据每一帧所受到的干扰程度的大小，SCL译码器自适应选择列表大小进行SCL译码。本节提出的自适应SCL译码器，控制逻辑简单，相比原始的SCL算法，能在保证译码性能的前提下，有效降低译码复杂度，尤其在高信噪比条件下，复杂度降低的程度明显。

2.1 信噪比等级预测算法

对于不同列表大小的SCL译码器的译码性能，存在这样一个事实：对于一些特定的信噪比，不同的列表大小却有相似的FER性能。例如，如图2所示，在信噪比SNR=2 dB时，列表大小L=8的SCL译码器和列表大小L=32的SCL译码器FER性能几乎完全一样，因此完全可以在该信噪比条件下，用列表大小L=8的SCL译码器取代列表大小L=32的SCL译码器进行译码。基于此，将信噪比区间 [1 dB,3 dB]划分为5个信噪比区间，每一个信噪比区间是一个信噪比等级，由低信噪比到高信噪比依次为信噪比等级1至5，且分别对应使用不同的列表大小进行SCL译码。本方案中，[1 dB,1.5 dB]为信噪比等级1，对应使用列表大小L=32的译码器；(1.5 dB,2 dB]为信噪比等级2，对应使用列表大小L=16的译码器；(2 dB,2.5 dB]为信噪比等级3，对应使用列表大小L=8的译码器；(2.5 dB,2.75 dB]为信噪比等级4，对应使用列表大小L=4的译码器；(2.75 dB,3 dB]为信噪比等级5，对应使用列表大小L=2的译码器。

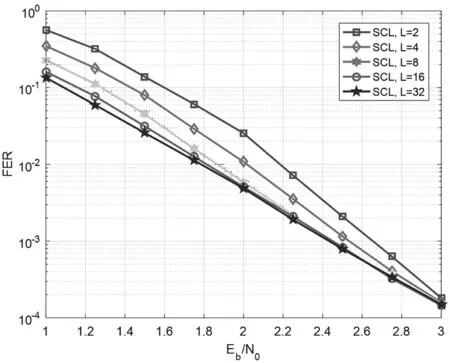
图2 不同列表大小的SCL译码算法性能，码长N=1 024，码率R=0.5

另一方面，一个码长为N、码率为R的Polar码，由K=N·R个信息比特和N-K=N-N·R个冻结比特组成。冻结比特是收发双方都已知的数据，通常设为0。每一帧Polar码码字经过AWGN信道，不仅仅信息位比特受到了信道的高斯白噪声干扰，冻结位比特同样也受到了同样信道条件下的噪声干扰。在大多数译码算法中，不管译码后冻结位比特的LLR值为多少，都将冻结位比特译码为0，而忽略它在一定程度上也包含了信道信息。目前，也有少量文献利用了冻结位进行信噪比估计。文献[8]在理论上证明了码长无限长时，[-5 dB,5 dB]范围内信噪比与冻结比特错误概率呈线性关系，如图3所示，且提出了有限码长下的信噪比预测算法，但是该算法包含了大量的蒙特卡罗仿真，实用性不强。因此，为了简单充分地挖掘冻结位信息，利用经过一次SC译码后的冻结位的LLR值作为反向传播神经网络的输入，然后估计每一帧所处的信噪比等级。

为了找到反向传播神经网络最佳的连接权值，必须知道一个已知的输入输出的映射关系和损失函数。根据前述内容，本方案中输入是每一帧冻结位比特的LLR值，输出是信噪比等级，损失函数是实际输出与期望输出的均方误差。通过使用梯度下降算法、反向传播算法和最小化损失函数，该神经网络能够对未知的输入产生正确的输出。

一般来说，获得神经网络的训练数据通常是一件很难的事情。但本方案是一个特殊例子，因为可以人为地产生任意多的输入信号和设定特定的信噪比[9]，且产生对应的输出信号非常简单，只要受过特定信噪比条件下干扰的码字一产生，就可以轻松得到其对应的输出，也就是该特定信噪比所处的信噪比等级。

图3 冻结比特错误概率与信噪比的映射关系

2.2 系统模型

在发送端，传输(1 024,512)Polar码，经过AWGN信道传输得到噪声帧。如图4所示，首先对接收到的噪声帧进行SC译码，取出其中M个冻结比特的LLR值，其中M≤512，M的大小是一个经验获得的值。对于Polar码而言，一些冻结比特的信道容量趋近于0，没有必要选择这些冻结比特的LLR值。一方面它很有可能降低结果的准确性，另一方面会带来巨大的计算复杂度。因此，对于 (1 024,512)Polar码，选择了150位冻结比特的LLR值作为神经网络的输入。

图4 基于反向传播神经网络的自适应SCL译码器

本方案采取了60-30-15-5的反向传播神经网络，即有2层隐含层，其节点数分别为30和15。至于神经网络的参数最优化问题，文献[9]已经提出了几种超参调优算法。但本方案中并没有更深入考虑这个问题，因为已经实现了较好的结果。通过反向传播神经网络，可估计每一帧的信噪比等级，再根据前述的信噪比等级与列表大小的映射关系选择列表大小，最后进行SCL译码，选择L条路径中最好的路径特性值作为译码输出。

3 仿真结果分析

对提出的自适应SCL译码方案进行仿真。仿真中，Polar码字构造方法采用高斯近似构造法，物理信道为AWGN信道，调制方式为二进制相移键控（Binary Phase Shift Keying，BPSK）。本节比较了自适应SCL译码器与原始的SCL译码器的FER性能和计算复杂度。

图5给出了不同列表大小的原始SCL译码器和自适应SCL译码器的FER性能比较。相比于列表大小L=2的原始SCL译码器，提出的自适应SCL译码器在中低信噪比条件下有近0.5 dB的增益，FER性能几乎与L=32的原始SCL译码器FER性能相近。

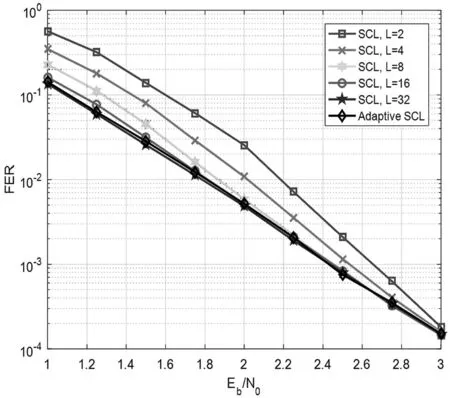
图5 原始SCL译码器与自适应SCL译码器FER性能比较，码长N=1 024，码率R=0.5

表1给出了不同信噪比等级下自适应SCL译码器和下降模式的自适应SCL译码器[4]的平均列表大小的比较。在所提方案中，首先进行SC译码，然后根据SC译码结果自适应地选择列表大小再进行SCL译码。因此，所提方案对每一帧都进行了两次译码，译码延时固定。一旦列表大小确定，提出的自适应SCL译码器的理论列表大小值应该为Lavg=L+1。由于反向传播神经网络存在一定预测误差，实际的平均列表大小值将会轻微大于或小于理论的平均列表大小值。因为通过反向传播神经网络预测信噪比等级和列表大小后进行SCL译码，所以所提方案在中高信噪比条件下能够有效减小SCL译码器的译码复杂度。因此，当在低信噪比条件下，自适应地选择较大的列表，就能保证SCL译码器的性能。

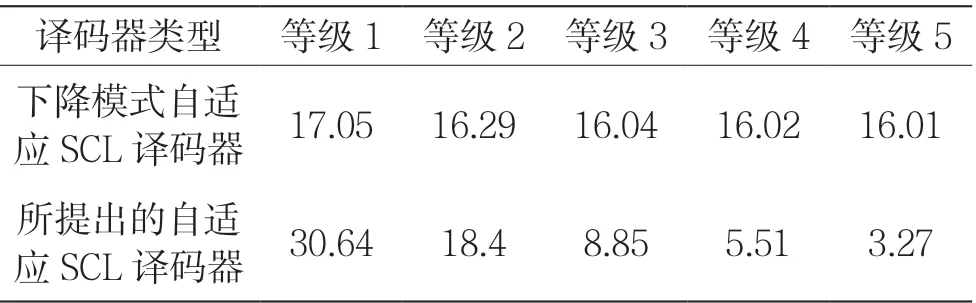
表1 下降模式自适应SCL译码器与所提出的自适应SCL译码器的平均列表大小比较

4 结 语

本文主要介绍了基于反向传播神经网络的自适应SCL译码算法，根据反向传播神经网络估计的信噪比等级，自适应地选择列表大小进行SCL译码。仿真结果表明，所提方案相比于L=32的原始SCL译码器，在中高信噪比条件下能够有效减小译码复杂度；相比于L=2的原始SCL译码器，在中低信噪比条件下能够有效提升FER性能。此外，所提方案对每一帧都是两次译码，其译码延时固定，且控制逻辑简单可控。