适用不同粒径含盐砂壤土水分扩散率的通用模式

古莱姆拜尔·艾尔肯，虎胆·吐马尔白,马合木江·艾合买提

(新疆农业大学水利与土木工程学院 ，新疆 乌鲁木齐 830052)

土壤水分运动参数包括土壤水分扩散率D(θ)、导水率K(θ)以及比水容量C(θ)，这些参数综合反映了土壤的持水性能及运移能力[1]。土壤水分扩散率反映了土壤孔隙度、孔隙大小分布以及导水性能，它是表征土壤水动力学的重要参数之一，并影响土壤中水分运动状况[2-3]。土壤水分扩散率也是研究水盐运动规律与调控的主要参数[4]。土壤扩散率受质地、粘粒含量、土壤密度、孔隙度和有机质等诸多因素的影响[5]。因此，半干旱地区土壤水分扩散率的研究具有极其重要的理论和实践意义，早已为人们所重视。长期以来，很多学者针对干旱、半干旱地区做了大量的研究工作[6-9]，但是研究土壤盐分对土壤水分扩散率的影响较少见。

用水平入渗实验计算土壤水分扩散率的方法最早是由Bruce和Klute提出的[10]。该方法是利用一个半无限长的水平土柱来进行入渗试验，忽略重力作用，根据一维水平流动的偏微分方程和定解条件，引入Boltzmann变换参数后，将偏微分方程化为常微分方程，用解析法求得计算公式，再由试验资料列表计算土壤水分扩散率[11]。随后，Kirkham和Powers[12]详细论述了这种方法的应用。因为该方法的关键是获得土壤水分分布的光滑曲线，因此得到了广泛应用[13-20]。此法为室内测定D(θ)的重要方法，在非饱和土壤水分运动研究中起到了重要作用。

土壤中的盐分运动十分复杂，盐分一般随着土壤水分的运动而迁移。由于新疆石河子121团是典型的重盐碱土，因此确定含盐土中水溶质运动的综合扩散系数是十分必要的。对盐碱地土壤水盐运动的定量描述是控制区域土壤次生盐碱化的基础，其中的土壤水分扩散率是研究土壤水盐运动不可缺少的参数之一[21-23]。本研究在建立Boltzmann变换参数η与土壤体积含水率θ定量函数关系的基础上，采用类似于Bruce和Klute的方法对新疆石河子121团灌区膜下滴灌棉田不同粒径含盐砂壤土土壤水分扩散率进行比较,以及对土壤盐分运动规律进行研究。通过水分扩散率的测定可定量模拟单位时间内土壤水分扩散率的距离及其与含水率之间的关系，预测土壤次生盐碱化的发展速度，为土壤次生盐碱化的监测与防治提供理论依据。

1 试验地概况

试验在新疆石河子121团进行，该团位于天山北麓，准噶尔盆地南缘，E85°20′～85°48′，N44°45′～44°58′。该地属于温带大陆性气候，日照时间长，年平均日照时间2 864 h，最高气温35℃，无霜期达160 d，年降水量140.2 mm,平均蒸发量1 789.2 mm，地下水埋深3～5 m，土壤质地为砂壤土。0～100 cm土层平均体积质量1.48 g·cm-3,田间持水率为20.6%(重量含水率)。

2 材料与方法

2.1 采样方法与数据测定

土样采自新疆石河子121团试验地，采用50 m×50 m网格取样，用自封袋装扰动土土样，采集117点共702个土样样品，试验地面积为450 m×650 m。土壤容重采用环刀法测定；土壤颗粒分析是用国际SL237-1999中密度计法测定颗粒组成，土壤类型由美国土壤类型三角图确定。其中粉粒占0.7%(0.002～0.05 cm)，粘粒占23.7%(<0.002 cm)，砂粒占75.6%(0.05～2 cm),土壤质地为砂质壤土，经自然风干后的土壤过0.5、0.5～1.0 mm和1.0～2.0 mm筛，按1.40 g·cm-3容重装入水平土柱中。

2.2 测定原理

测定原理参见文献[24]。在水平土柱中，使进水端维持接近饱和的稳定边界的土壤含水率，使水分在土柱中作水平渗吸运动，在不计重力影响的条件下进行测定。其一维水平流的微分方程和定解条件为：

(1)

θ(x,t)=θix>0,t=0

(2)

θ(x,t)=θs,x=0,t>0

(3)

式中,t为时间(min)，x为水平入渗距离(cm)，D(θ)为非饱和土壤水分扩散率(cm2·min-1)，θi为水平土柱初始含水率，θs为饱和含水率(开始试验后在边界处瞬时形成)

对式(1)进行波尔兹曼变换(Boltzmann),利用定解条件(2)和(3)式，可以求得：

(4)

式中,η为波尔兹曼参数，η=xt-1/2。

为了便于计算，通常将式(4)改变为差分的形式，其表达式为：

(5)

通过对(5)式的计算，便可根据实验数据，用列表法计算土壤水分扩散率D(θ)。

2.3 实验装置

水平土柱试验装置见图1，土柱由有机玻璃圆筒(内径为4.6 mm)组成。试样段由13个长4 cm的圆环组成。在进水边界处(x=0)，为保证土壤体积含水率为饱和含水率但又不产生重力水流的条件，在进水室与土柱之间装设低气泡压力和高传导率的多孔板或滤网。供水装置用以控制水平土柱的作用水头(可考虑保持土柱作用水头略低于大气压力)，测量进水量。

图1 土壤水分扩散率试验装置示意图Fig.1 Schematic diagram of test equipment for determining soil water diffusivity

2.4 实验步骤

(1)制备土样及装填土柱，准备好足够的试样(风干含水量)。按一定容重装填土柱，将螺杆旋紧然后水平放置。(2)瞬时给进水室充水并使供水装置定位。(3)计时并记下供水箱初始水位读数。(4)经过相当时间(湿润锋面未达土柱末端之前)后，即可结束试验，此时停止供水，松开坚固螺杆，按节取出土壤测定含水率，记下整个试验的历时及总水量。3个重复试验。(5)利用烘干法将烘干土样粉粹，取土水比例1∶5搅拌均匀，沉淀后利用DDSJ-308A土壤含盐率仪测定土壤的含盐率(3个重复)。

3 结果与分析

3.1 土壤体积含水率与Boltzmann变换参数和土壤含盐率的关系

通过非稳定流水平土柱试验，得到三组试验数据，用式η=xt-1/2算出不同θ值对应的η值，并绘制θ-η曲线(图2)，Boltzmann参数η=xt-1/2(x为水平入渗距离，t为时间)反映了水分在土壤中水平入渗时，湿润峰向前移动的快慢程度[7]。在进水端土壤体积含水率接近饱和，Boltzmann变换参数应为零；当土壤体积含水率取初始体积含水率时，Boltzmann变换参数趋于无穷大。从图可知土壤体积含水率随着Boltzmann变换参数的增大而减少。

对粒径<0.5 mm、0.5～1.0 mm和1.0～2.0 mm，当体积含水率范围分别在0.367、0.332、0.317 cm3·

图2 土壤体积含水率(θ)与Boltzmann参数(η)的关系Fig.2 Relationship between soil water content θ and Boltzmann transformation parameter η

cm-3以上时，Boltzmann变换参数随体积含水率缓慢下降；在体积含水率低于0.367、0.332、0.317 cm3·cm-3时，随着体积含水率的降低，Boltzmann变换参数迅速下降。

土壤盐分一般随着土壤水分的运动而迁移。由土壤体积含水率与土壤含盐率的变化关系(图3)可知，土壤含盐率随着土壤体积含水率的增大而减少，<0.5 mm粒径的砂壤土的含盐率最高；接下来是0.5～1.0 mm粒径的砂壤土；最低的是1.0～2.0 mm粒径的砂壤土。这是因为土壤累计入渗时间和总入渗水量随着粒径的增大而减少。土壤含盐率与土壤体积含水率的关系可用线性函数来表示(表1)。从土壤体积含水率与Boltzmann变换参数和土壤含盐率之间的关系分析可知Boltzmann变换参数和土壤含盐率随着土壤体积含水率的增大而减少。

图3 土壤体积含水率(θ)与土壤含盐率(S)的关系Fig.3 Relationship between soil water content (θ)and soil salt content (S)

3.2 土壤体积含水率与土壤水分扩散率的关系

根据实验数据计算不同体积含水率对应的土壤水分扩散率，并绘制土壤体积含水率与土壤水分扩散率的关系曲线(图4)。

从图中可以看出，对于同一容重、相同水平距离情况下粒径不同时含盐砂壤土的土壤水分扩散率随土壤体积含水率的增加而增加。当含水率接近饱和时，水分扩散率趋于无穷。1.0～2.0 mm的砂壤土扩散率最大，而且变化比较迅速，其次0.5～1.0 mm的砂壤土，最小的是小于0.5 mm的砂壤土。这表明土壤机械组成对土壤水分扩散率有较大的影响，表现为随着土壤粒径的减小，土壤水分扩散率逐渐降低。这与Xie Senchuan等[25]的砂性土的非饱和土壤水分扩散率大于粘性土的结论一致。用指数函数拟合土壤水分扩散率与土壤体积含水率之间的关系，具体结果见表2。

3.3 土壤水分扩散率的综合通用表达式

在实际情况中，仅仅土壤体积含水率与土壤水分扩散率的经验公式受到一定的限制，不能较好地反映出土壤水分扩散率的变化曲线。因此要找到一个计算不同粒径含盐沙壤土水分扩散率的通用公式。

表1 土壤体积含水率与土壤含盐率的线性函数拟合分析

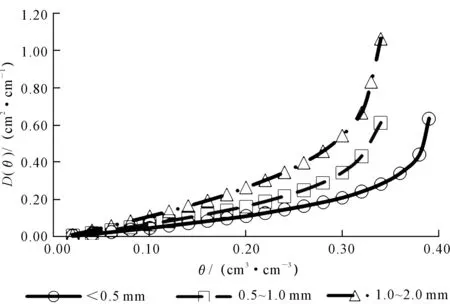
图4 土壤体积含水率θ与土壤水分扩散率D(θ)的关系曲线Fig.4 Relationship between soil water content (θ) and soil water diffusivity D(θ)

由土壤体积含水率与土壤含盐率的变化关系可知，土壤含盐率随着土壤体积含水率的增大而减少，土壤含盐率与土壤体积含水率的关系可用线性函数来表示(表1)。通过分析土壤体积含水率与土壤含盐率之间关系，再结合土壤体积含水率与土壤水分扩散率之间关系，可知土壤含盐率随着土壤水分扩散率的增大而减少。本文通过上述分析了土壤水分扩散率与土壤体积含水率和土壤含盐率的变化关系，得到了土壤水分扩散率的综合表达式(见表3)。试验分析得出，同一容重、相同水平距离情况下粒径不同时含盐沙壤土拟合的经验公式，拟合程度和回归程度较好。

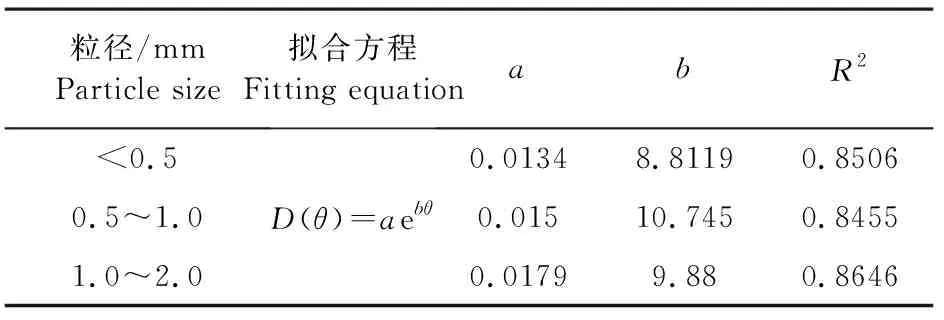
表2 土壤体积含水率与土壤水分扩散率的指数函数拟合分析

表3 土壤水分扩散率的综合表达式

4 结果与讨论

1)对于同一容重、相同水平距离情况下粒径不同时含盐砂壤土的土壤体积含水率与土壤水分扩散率呈单调递增关系。1.0～2.0 mm的砂壤土扩散率最大，而且变化比较迅速，其次为0.5～1.0 mm的砂壤土，最小的是小于0.5 mm的砂壤土。随着土壤粒径的减小，土壤水分扩散率在逐渐降低。当土壤体积含水率接近饱和时，水分扩散率趋于无穷。

2)对于同一容重、相同水平距离情况下粒径不同时含盐砂壤土的土壤含盐率与土壤水分扩散率呈单调递减关系。<0.5 mm粒径的砂壤土的含盐率最高，其次为0.5～1.0 mm粒径的砂壤土,最低的是1.0～2.0 mm粒径的砂壤土。

3)新疆盐碱地土壤面积较大，土壤水分运动参数计算中考虑土壤的含盐量是较为符合实际。土壤水分扩散率D(θ)的通用模式中综合考虑土壤体积含水率和土壤含盐率，得出的经验公式能够较好地反映不同粒径含盐砂壤土的土壤水分扩散率。