沼液穴灌入渗特征及Philip入渗模型拟合

郑 健,张彦宁,王 燕,张恩继

(1.兰州理工大学西部能源与环境研究中心，甘肃 兰州 730050；2.甘肃省生物质能与太阳能互补供能系统重点实验室，甘肃 兰州 730050；3.兰州理工大学能源与动力工程学院，甘肃 兰州 730050)

我国在“十二五”规划期间，户用沼气和规模化沼气工程发展迅速，利用生物质能已经是我国村镇能源建设的主要方向之一。截止2015年底，我国已有5000多万口户用沼气池[1]。但沼气的生产伴随着沼液的产生，大量沼液的随意排放，必然会对环境造成危害。中国农业部于2015年印发的《到2020年化肥使用量零增长行动方案》[2]中提倡采用有机肥替代化肥，而沼液是一种含有水溶性及多种养分的速效有机肥，更易于植物吸收利用[3]。国内外相关研究也多集中于沼液灌溉对作物产量[4-6]及品质[7-9]、地下水水质[10]、土壤中重金属累积[11-12]以及土壤肥力[13-15]的提高等方面，而对于沼液土壤入渗机理的基础性研究鲜见报道。课题组在调研过程中发现农民灌溉施用的沼液粘性较纯水高且含有一定量的有机悬浮颗粒，而研究表明沼液中的有机悬浮颗粒有利于土壤环境改善[16-17]，但从土壤入渗角度分析液体的粘性[18]和颗粒含量均会对土壤入渗特性产生不可忽略的影响[19-21]。因此，为使沼液在农田中更科学、合理的应用，有必要针对沼液特点开展入渗特征研究。

沼液穴灌技术是农民在设施农业生产中总结的一种节水、节肥技术，具有简单、低成本、易操作的特点，现在已经成为农村沼液应用的最主要方式之一。但目前该技术的实施主要根据经验，对其相关的试验研究和理论分析还少见报道。基于此，本文以沼液穴灌技术为基础，通过室内试验研究分析沼液配比、穴孔直径和土壤容重对土壤入渗特征的影响，利用数理统计方法分析影响沼液穴灌入渗的因素和湿润体变化规律，同时应用具有明确物理意义的Philip入渗模型对沼液穴灌累积入渗量进行拟合分析。以期为获得合理的沼液穴灌技术参数提供理论支撑，解决水/沼液一体穴灌技术在实际应用中遇到的问题。

1 材料与方法

1.1 试验材料及装置

试验土壤取自甘肃省兰州市周边正常使用的温室大棚表层0～40 cm的土壤，经过自然风干、粉碎后，过2 mm孔径的土壤筛备用，土壤颗粒级配见表1，按照中国土壤分类标准其土壤类型为粉质壤土，田间持水量为22.23%(质量含水率)。沼液取自正常使用的户用沼气池，原料以牛粪和麦秸为主，发酵物总固体质量分数(TS)为8%，经曝气静置2个月，待其理化性质稳定后，用纱布过滤掉沼液中较大的颗粒备用。试验装置主要由土箱和马氏瓶组成，如图1所示。土箱为30°扇形有机玻璃装置，高和宽分别为50 cm和40 cm，马氏瓶用来提供恒定水头，容量520 mL。

1.2 试验设计

试验设置土壤容重、沼液浓度和穴孔直径3个控制因素。土壤容重为1.35 g·cm-3和1.45 g·cm-3，依据前期预试验结果，设置4个沼液与水的配比(沼液∶水，体积比)，分别为1∶4、1∶6、1∶8和纯水(CK)，3个穴孔直径，分别为3、5 cm和7 cm，设定孔深为5 cm。每组试验设置两组重复，共计72组试验，取平均值作为试验结果。

1.3 试验方法

1.3.1 沼液理化性质 试验开始前测定不同配比的理化性质，采用电导率仪(雷磁DDS-11A)测定不同浓度沼液的电导率值；利用烘干称量法测量不同浓度沼液中的干物质质量；利用奥氏粘度计测定不同浓度沼液的相对粘度；全氮含量采用凯式定氮法测定；硝态氮含量采用紫外分光光度计测定[22]；铵态氮采用纳氏试剂比色法测定[22]。测定结果见表2。

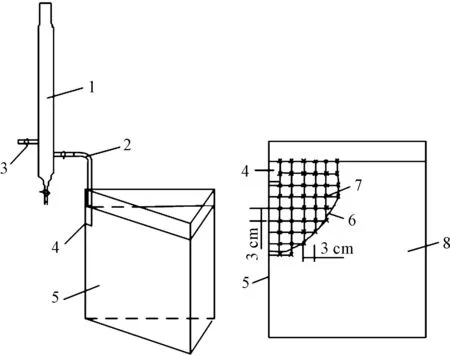
1.马氏瓶;2. 进水管;3.排气管;4.穴孔; 5.土槽;6.湿润峰;7.取样点;8.土体1. martensitic bottle;2. inlet pipe;3. exhaust pipe;4. soil hole; 5. soil bin;6. wetting front;7. sampling point;8. soil图1 试验装置及取样示意图Fig.1 Schematic diagram of the test equipment and sampling

1.3.2 穴灌试验 试验土体采用分层填装(每层5 cm)，依据土壤容重计算每层装土质量，用电子秤(感量为0.01 g)称量；按设定沼液与水的配比装入马氏瓶，用乳胶软管将马氏瓶出水孔与试验土槽连接。为方便在试验中记录数据，根据实际穴灌湿润体的形状，在土槽边壁绘制间距5 cm的网格线。然后，同时打开马氏瓶出水孔和排气孔阀门，当沼液进入穴孔时开始计时，随着试验的进行，当湿润峰运移到与水平或者垂向的网格线相切时(网格密度5 cm×5 cm)，记录一次入渗时间和累积入渗量，并用记号笔在土槽边壁上绘制湿润锋运移曲线。当入渗量达到520 ml(马氏瓶最大容量)或者入渗时间达到10 h以上时，关闭马氏瓶的进水孔和排气孔阀门，待穴孔内沼液入渗完，试验结束，立即取土样测定土壤质量含水率。

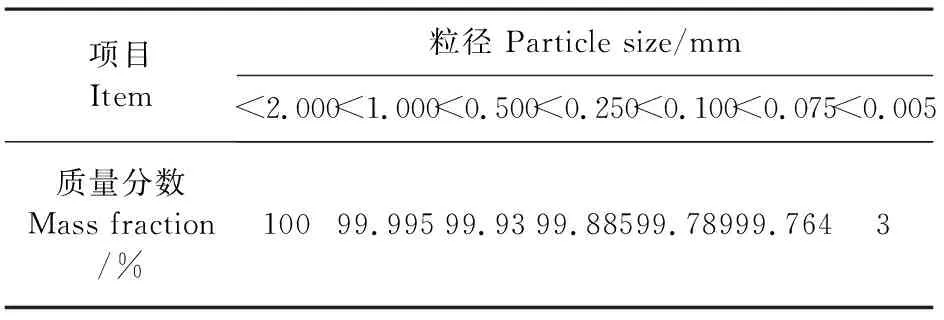
表1 土壤颗粒级配

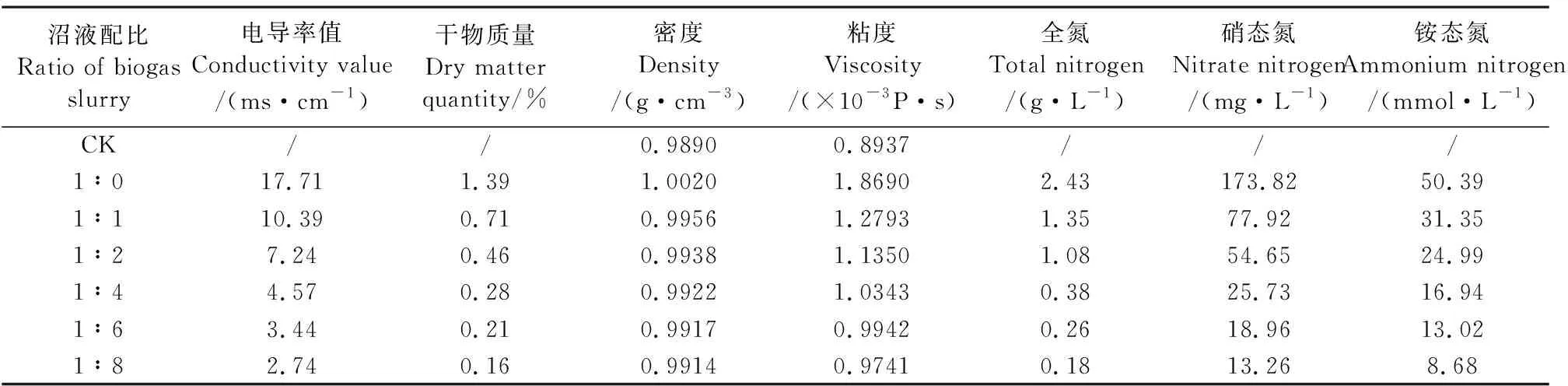
表2 不同配比沼液理化性质

2 结果与分析

2.1 沼液穴灌土壤入渗规律

2.1.1 累积入渗量变化规律 由图2可以看出，不同试验处理的累积入渗量在初始阶段增加较快，随着入渗历时的延长，累积入渗量增加幅度逐渐降低，其中CK处理累积入渗量增加幅度明显大于沼液处理。相同土壤容重及沼液配比条件下累积入渗量随着穴孔直径的增加而增大。在相同土壤容重及穴孔直径条件下累积入渗量随着沼液配比的降低而增大。当入渗历时180 min时，容重为1.45 g·cm-3的CK处理累积入渗量分别是沼液配比为1∶4、1∶6、1∶8处理的3.47、2.64、2.16倍；容重为1.35 g·cm-3的CK处理累积入渗量分别是浓度为1∶4、1∶6、1∶8处理的3.62、3.12、2.77倍。

初步分析产生的原因为：(1)在入渗初始阶段，表层土壤干燥，含水率较低，土壤基质势较大，基质吸附力起主要作用，另一方面，由于表层土壤存在相互连通的大孔隙和传导孔隙[23]，水分入渗的气相阻力较低，其毛管作用也较为明显，故初始累积入渗量增加较快，随着入渗试验的进行，土壤的含水率逐渐增加，土壤表层水分饱和层也逐渐加厚，土壤基质的吸力梯度逐渐减弱，加上通气孔隙的减少，气相阻力逐渐增大，毛管作用随之降低，入渗速率也逐渐降低，当入渗进行到一定时间后，土壤基质的吸力梯度和毛管作用趋于零，在重力作用下，入渗速率会维持在一个较为稳定的水平上[24-25]。(2)穴灌过程中，累积入渗量受到土壤基质势作用影响，同时重力势的影响也不可忽略。随着穴孔直径的增加，重力势的作用越显著，在入渗过程中，土壤基质势作用逐渐降低，重力势起主导作用，致使累积入渗量随着穴孔直径的增加呈递增趋势。(3)沼液入渗过程中，沼液中的有机悬浮颗粒在土壤的表层沉积，形成沉积层，与CK处理相比，该沉积层改变了穴灌入渗的边界条件，起到了阻渗作用，并且随着沼液中有机悬浮颗粒含量的增加阻渗作用越明显。同时，由于液体在土体中的流动速度慢，土壤孔隙小(当土壤容重为1.35 g·cm-3时，当量孔径0.03 mm以上占10.26%、0.03～0.0038 mm占16.50%、0.0038～0.0004 mm占7.7%，而0.0004 mm以下占64.54%[26])，液体在土壤中的流态为层流，而层流状态下液体的粘性会增加液体运动的阻力[18]。

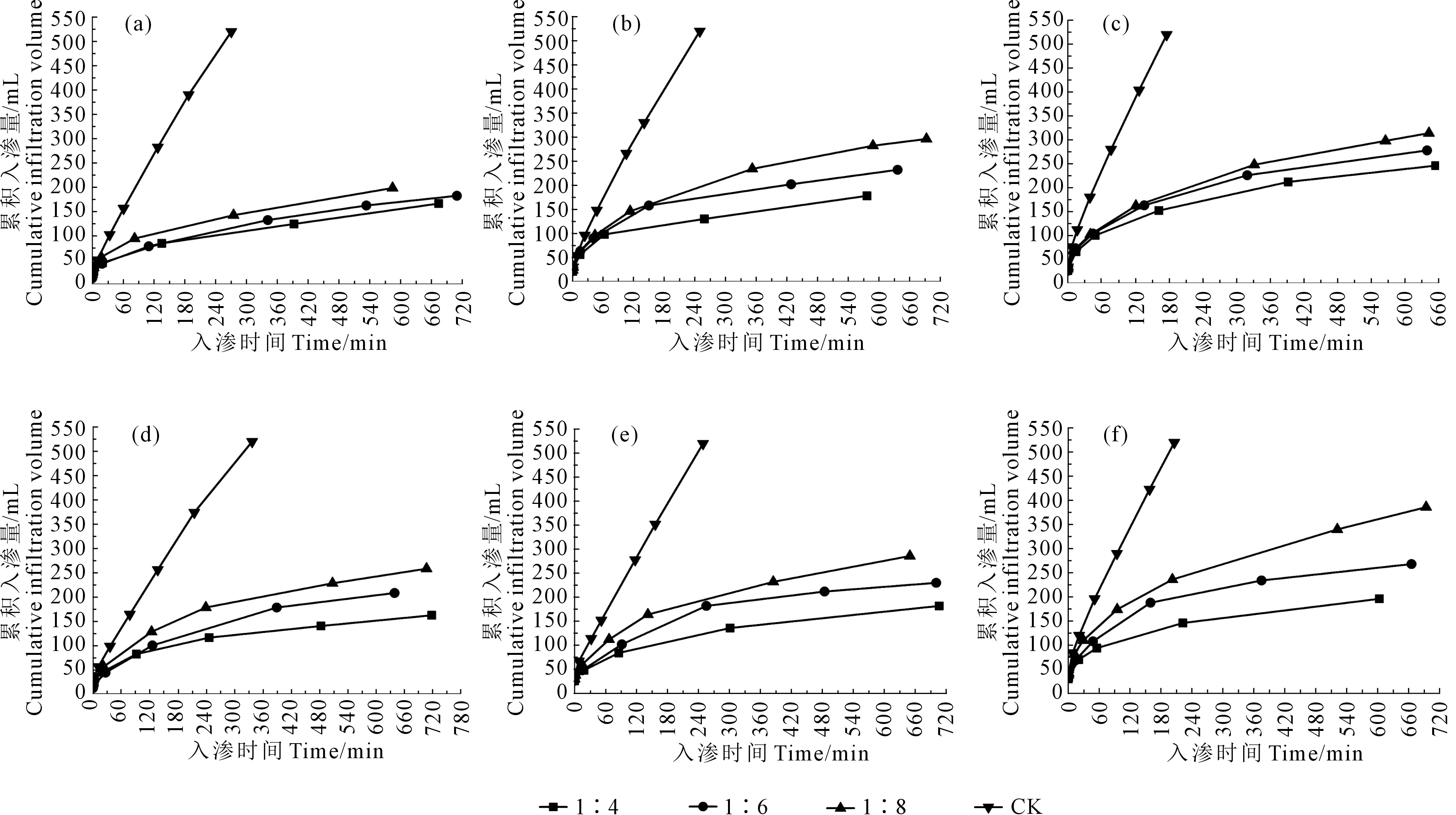
注：a.土壤容重1.35 g·cm-3, 孔径3 cm;b. 土壤容重1.35 g·cm-3, 孔径5 cm;c. 土壤容重1.35 g·cm-3, 孔径7 cm;d. 土壤容重1.45 g·cm-3, 孔径3 cm;e. 土壤容重1.45 g·cm-3, 孔径5 cm;f. 土壤容重1.45 g·cm-3, 孔径7 cm。Note: a. soil bulk density 1.35 g·cm-3, hole diameter 3 cm; b. soil bulk density 1.35 g·cm-3, hole diameter 5 cm; c. soil bulk density 1.35 g·cm-3, hole diameter 7 cm; d. soil bulk density 1.45 g·cm-3, hole diameter 3 cm; e. soil bulk density 1.45 g·cm-3, hole diameter 5 cm; f. soil bulk density 1.45 g·cm-3, hole diameter 7 cm.图2 不同处理对沼液累积入渗量的影响Fig.2 The influence of different treatment on the cumulative infiltration volume of biogas slurry

2.1.2 累积入渗量影响因素分析 为进一步阐明不同土壤容重、穴孔直径和沼液配比与累积入渗量之间的关系，应用数理统计方法建立了累积入渗量(It)与土壤容重(x1)、穴孔直径(x2)和沼液配比(x3)间的经验模型，并对其偏回归系数值进行了检验。回归分析及方程检验结果如式(1)所示。

(1)

式中,It为累积入渗量,x1为土壤容重,x2为穴孔直径，x3为沼液配比，*为P=0.05水平上差异显著，**为P=0.01水平上差异显著。

由式1可以看出，累积入渗量与土壤容重、穴孔直径和沼液配比回归方程的决定系数(R2)值达到了0.91，各影响因子t检验分别为0.40、2.94、-13.86，均到达了显著和极显著水平，P检验均小于0.05。表明该回归方程拟合度较高，适应性较好。回归方程中累积入渗量与土壤容重、穴孔直径和沼液配比的偏回归系数检验均达到显著或极显著水平，即土壤容重、穴孔直径和沼液配比的变化均会对累积入渗量产生影响。

从回归方程各因素的拟合系数分析，穴孔直径与累积入渗量呈正相关，土壤容重、沼液配比与累积入渗量呈负相关，即随穴孔直径增加累积入渗量呈逐渐增大趋势，而随土壤容重、沼液配比的增加累积入渗量呈逐渐减小趋势。从系数值的大小来看，试验中沼液穴灌受沼液配比的影响最大，土壤容重次之，穴孔直径最小。因此，沼液穴灌过程中，要充分考虑土壤容重、穴孔直径和沼液配比耦合作用对累积入渗量的影响。

2.2 沼液穴灌湿润体形状变化规律

以穴孔底部的水平直线为水平轴，穴孔侧壁与土壤接触面为垂直轴建立坐标系，量取实测不同处理的水平最大湿润距离(H)和垂向最大湿润距离(V)，并建立函数关系，分析湿润体变化规律，结果如表3所示。由表可知：穴孔直径为3 cm时水平最大湿润距离大于垂向最大湿润距离，穴孔直径为5 cm和7 cm时水平最大湿润距离小于垂向最大湿润距离，且差异随穴孔直径的增加而增大，表明随穴孔直径的增加，湿润体形状会逐渐由水平轴大于垂直轴的椭球体趋向于水平轴小于垂直轴的椭球体；土壤容重为1.45 g·cm-3各处理的湿润体水平最大湿润距离与垂向最大湿润距离差异明显小于土壤容重为1.35 g·cm-3的各处理，结果表明相同处理条件下土壤容重的增加会使湿润体趋向于球体。

形成上述规律的主要原因为：(1)入渗初期基质势作用是湿润锋运移的主要驱动力，穴孔直径为3 cm时，沼液与穴孔边壁的接触面积大于其底面积，因而受到基质势的影响作用比穴孔直径为5 cm和7 cm时更大，使得水平湿润距离大于垂向湿润距离。随穴孔直径的增加，重力势作用逐渐大于基质势，使湿润锋在水平方向上的运移速率逐渐小于垂直方向上的运移速率；(2)同一质地土壤大孔隙比例均随土壤容重增大而递减[27]，而土壤中大孔隙比例的降低减弱了压力势对土壤垂向入渗的影响。

2.3 沼液穴灌湿润锋运移拟合分析

穴灌入渗中水平最大湿润距离(H)与垂向最大湿润距离(V)呈线性关系(见表3)，为进一步分析穴灌条件下湿润锋运移与时间的关系，将水平最大湿润距离(H)随时间的变化曲线采用y=mxn进行拟合，结果如表4所示。拟合结果中各处理拟合指数(n)均小于1，说明当入渗时间趋于无穷大时，单位时间湿润距离的增加速率逐渐减小并最终趋于稳定。拟合方程决定系数(R2)均在0.97以上，说明穴灌入渗时湿润锋的最大湿润距离与时间的函数关系可以用幂函数进行描述。

2.4 沼液穴灌Philip入渗模型拟合分析

Philip入渗模型具有结构简单、参数少、物理意义明确的特点，便于建立其特征参数与土壤物理特征间关系，并在田间入渗试验资料中得到了很好的验证[28]。因此，本文采用Philip入渗模型对沼液穴灌累积入渗量进行拟合分析。

Philip入渗模型是根据垂直入渗的级数解获得的，其累积入渗量可表示为[29]：

I(t)=St0.5+At

式中,I(t)为累积入渗量(mL)，t为入渗时间(min)，S为土壤吸渗率(mL·min-0.5)，A为土壤稳定入渗率(mL·min-1)。

分析Philip入渗模型拟合结果发现(见表5)：(1)Philip入渗模型中土壤稳定入渗率(A)在沼液处理中的值均为负值，CK处理中均为正值，且随着穴孔直径的增加而增大。(2)Philip入渗模型能够准确描述沼液穴灌累积入渗量随时间的变化规律，决定系数R2均在0.98以上。(3)土壤容重及沼液配比一定时，土壤吸渗率(S)随穴孔直径的增大而增加；土壤容重及穴孔直径一定时，土壤吸渗率(S)随沼液配比的降低而增加，即1∶4<1∶6<1∶81.45 g·cm-3。

Philip入渗模型表明，在入渗初期，土壤吸渗率(S)起主要作用，随着入渗时间的增长，土壤稳定入渗率(A)则成为影响入渗的主要因素[29]，且通常为正值。管瑶等[30]在土壤点源入渗自动测量系统监测滴头下土壤湿润过程研究中采用Philip入渗模型进行拟合分析时出现土壤稳定入渗率(A)为负值的结果，作者分析这可能与Philip模型的衰减系数固定为-0.5相关，-0.5的衰减系数限制了Philip入渗模型只能适用于某些特定土壤。但范严伟等[28]采用Philip入渗模型对中壤土、沙壤土、壤土和沙土进行拟合分析的结果表明土壤累积入渗量变化过程符合Philip模型，且土壤稳定入渗率(A)为正值。国内外学者王全九[31]、史晓楠[32]和Alagna V.[33]等对Philip入渗模型的研究也表明Philip入渗模型对不同土壤均具有较好的适应性。同时，本文采用Philip入渗模型进行拟合分析时，沼液处理土壤稳定入渗率(A)为负值，而CK(纯水)处理为正值。因此，本文认为沼液穴灌中土壤稳定入渗率(A)为负值，与沼液的粘性及所含有的有机悬浮颗粒有关。土壤吸渗率(S)随穴孔直径、沼液配比和土壤容重变化规律产生的原因，与累积入渗量变化规律形成原因相同。

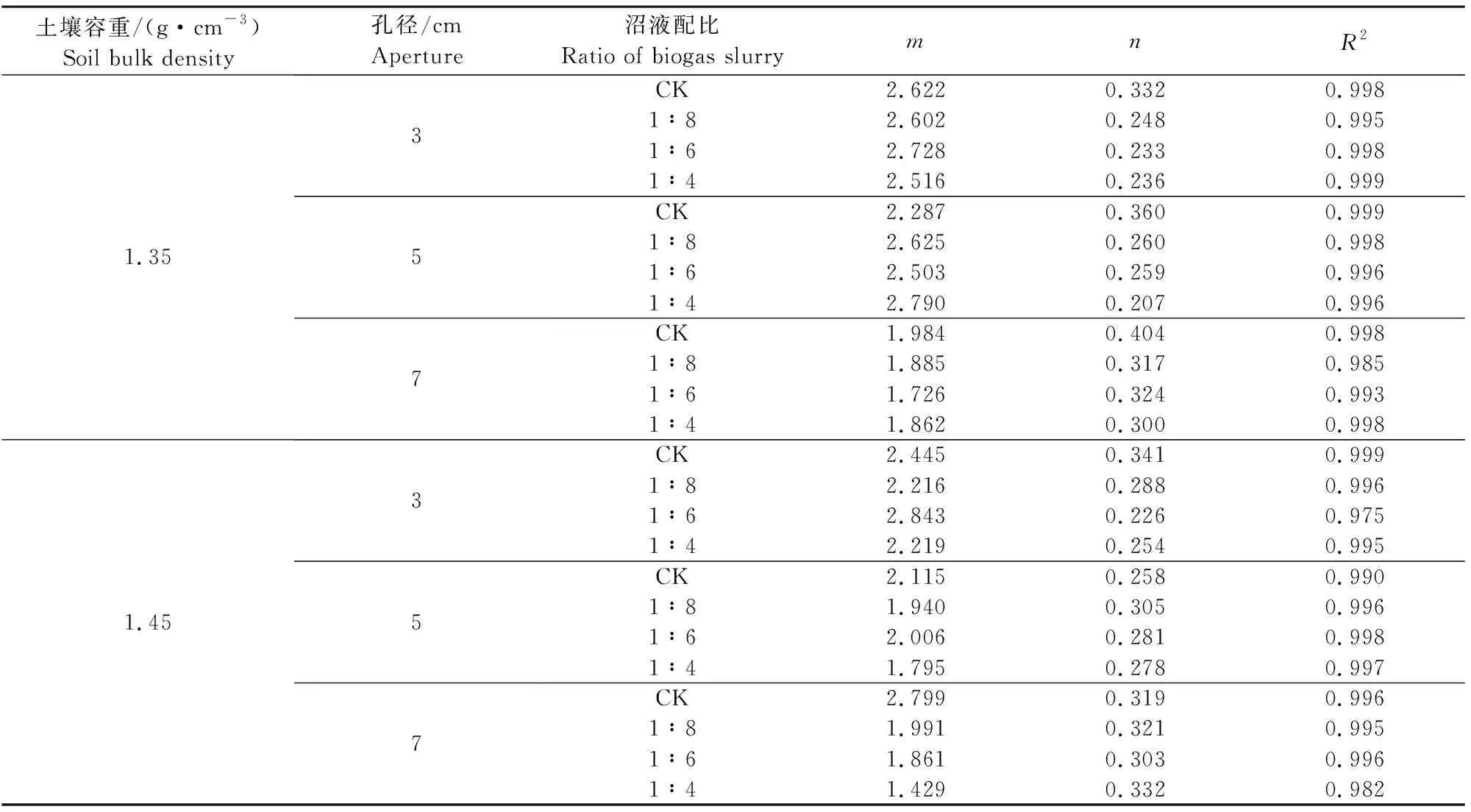
表4 水平最大湿润距离与时间拟合参数

表5 Philip入渗模型拟合参数

Table 5 Fitting parameters of Philip infiltration model

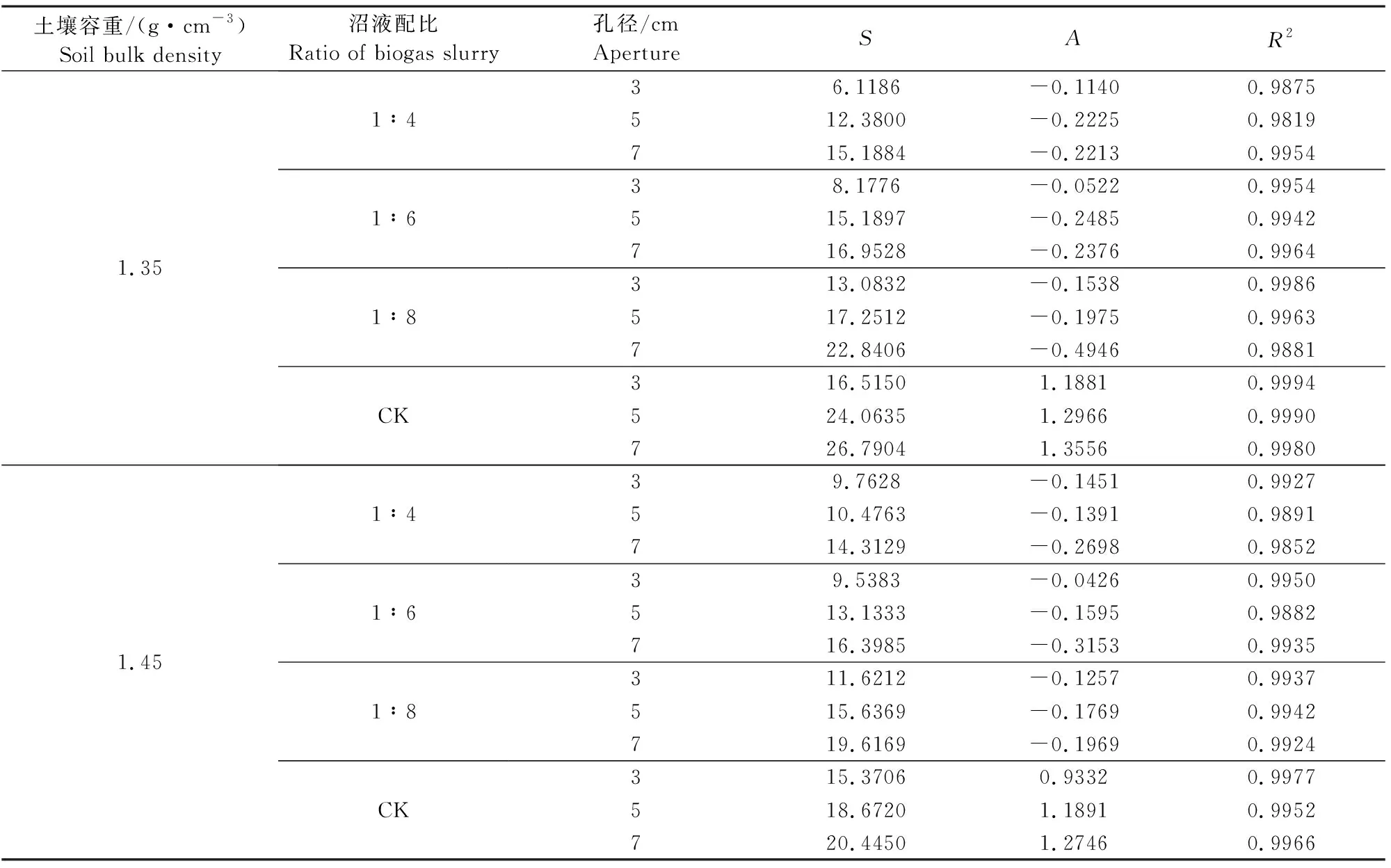
土壤容重/(g·cm-3)Soil bulk density沼液配比Ratio of biogas slurry孔径/cmAperture SAR21.351∶41∶61∶8CK36.1186-0.11400.9875512.3800-0.22250.9819715.1884-0.22130.995438.1776-0.05220.9954515.1897-0.24850.9942716.9528-0.23760.9964313.0832-0.15380.9986517.2512-0.19750.9963722.8406-0.49460.9881316.51501.18810.9994524.06351.29660.9990726.79041.35560.99801.451∶41∶61∶8CK39.7628-0.14510.9927510.4763-0.13910.9891714.3129-0.26980.985239.5383-0.04260.9950513.1333-0.15950.9882716.3985-0.31530.9935311.6212-0.12570.9937515.6369-0.17690.9942719.6169-0.19690.9924315.37060.93320.9977518.67201.18910.9952720.44501.27460.9966

3 结 论

1)沼液穴灌累积入渗量随着沼液配比和土壤容重的增大而降低，随着穴孔直径的增加而增大；CK处理累积入渗量增加幅度明显大于各沼液配比处理；应用数理统计方法建立的累积入渗量与土壤容重、穴孔直径和沼液配比的回归方程，决定系数R2值达到0.91，拟合良好。表明在沼液穴灌实施中要充分考虑土壤容重、穴孔直径和沼液配比耦合作用对累积入渗量的影响。

2)随穴孔直径的增加，沼液穴灌形成的湿润体形状会逐渐由水平轴大于垂直轴的椭球体趋向于水平轴小于垂直轴的椭球体；相同沼液配比和穴孔直径条件下土壤容重的增加会使湿润体趋向于球体；沼液穴灌湿润锋最大湿润距离与时间的函数关系可以用幂函数进行描述。

3)Philip入渗模型能够准确描述沼液穴灌累积入渗量随时间的变化规律，决定系数R2均在0.98以上；土壤吸渗率(S)随穴孔直径的增大而增加，随沼液配比和土壤容重的增加而降低；土壤稳定入渗率(A)为负值，与沼液的粘性及所含有的有机悬浮颗粒有关。

4)综合考虑土壤容重、穴孔直径和沼液配比对累积入渗量和湿润体变化的影响，建议的实施方案为：1.35 g·cm-3、5 cm、1∶6和1.45 g·cm-3、7 cm、1∶8。