基于病态指数循环分析的评价指标筛选研究

陈洪海

(南京财经大学金融学院，江苏 南京 210023)

1 引言

评价是人类最为常见的一种认知活动，是科学决策的基础。而评价一个事物所涉及因素通常较为繁多，这就需要在多个因素相互作用下对评价对象的水平或状态做出一种综合性的判断[1]。这便是多指标(多属性)综合评价，简称综合评价。

评价指标体系是进行综合评价的基础。协同学理论认为一个复杂系统的有序结构仅仅通过少量的参量即可有效描述，所有子系统主要受少数指标支配[2]。由此可见，一组评价指标作为相互影响、相互作用的一个系统，其内部评价指标的数量绝非多多益善。因此，评价指标体系的建立离不开评价指标的筛选。其内在原因主要有二：一是众多指标中不可能每个指标均对评价结果有显著影响，即不可能每个指标都重要。事实上，有些指标对评价结果的影响是微弱的，仅是评价者经验性地认为这些指标重要而已，而主观经验却未必客观可靠。二是即使被保留的指标均对评价结果影响显著，这些指标间也极有可能存在较严重的相关性，即指标间的信息重叠程度可能较高。这些重叠信息若不加处理，在综合评价时会被反复强调，进而扭曲综合评价结果[3]。尽管主成分分析、因子分析等降维方法在理论上回避了指标间的信息重叠，但却产生了主成分的经济含义难于确定及因子载荷矩阵不唯一等问题。因此，指标间信息重叠的降低依然主要通过剔除指标集中部分指标的方式实现。而且，根据评价指标筛选的内在原因可知，综合评价指标定量筛选的两大核心任务就是剔除重要性差的指标，及降低指标集的信息重叠。

评价指标体系及综合评价方法是综合评价理论最核心的两部分内容。其中，评价指标体系是综合评价的基础，直接影响综合评价的科学合理性。但遗憾的是，目前已有研究在关注综合评价方法的同时，却并未对用于建立评价指标体系的指标筛选方法予以足够的重视。这直接导致评价指标筛选方法研究的明显滞后。目前，评价指标的筛选主要以定性与定量两种方式实现。定性筛选指标的主观性太强，所以先利用专家经验进行评价指标的海选，再对海选指标进行定量筛选的方法日益受到欢迎。根据指标筛选目的的差异，通过指标筛选建立评价指标体系的定量方法主要分为两类。

一是以剔除重要性较差指标为目的的指标筛选方法，这里称之为关键指标遴选方法。比如Changki等[4]通过剔除信息增益相对较小的指标，实现了指标的筛选。Zhu Zexuan等[5]结合遗传算法与马尔可夫毯网络算法筛选关键指标。Inza等[6]基于贝叶斯网络估计算法提出了一种随机搜索指标筛选方法。Zhang Yudong等[7]基于决策树方法提出了一种带变异算子的二进制指标筛选方法。Aytug[8]基于广义的Benders分解法及支持向量机算法进行了指标的筛选。迟国泰等[9]通过比较信息敏感性的相对大小，剔除了解释原始指标集信息能力较弱的指标。李鸿禧和迟国泰[10]通过DEA-t检验遴选了对效率评价影响显著的指标。

二是以降低指标间信息重叠为目的的指标筛选方法，这里称之为信息重叠指标筛选方法。剔除重要性较差指标的筛选方法并未考虑大量指标彼此之间错综复杂的相关性，即信息重叠。而指标间的重叠信息在综合评价时会被重复性地予以强调，导致综合评价结果的失真。因此，已有研究在剔除了重要性较差的冗余指标后，通常会以剔除部分指标的方式降低评价指标间的信息重叠，以保证评价指标体系的科学合理。遗憾的是，目前降低指标集信息重叠的指标筛选方法较为少见。根据降低指标间信息重叠方式上的差异，已有信息重叠指标筛选方法的研究可分为两类。

(1)通过剔除相关程度高的两个指标中相对不重要的一个指标，降低指标集的信息重叠。范柏乃[11]、张昆等[12]、迟国泰等[13]、陈洪海等[14]及赵志冲等[15]通过剔除Person相关系数绝对值大的任意两个指标中相对不重要的一个指标，降低了指标集的信息重叠。这是目前应用得最为广泛的信息重叠指标筛选方法，称之为Person相关分析法。而韩伯棠等[16]、Destrero等[17]则分别通过剔除偏相关系数绝对值、互信息大的任意两个指标中相对不重要的一个指标，实现了指标集信息重叠程度的降低。

(2)仅保留通过R型聚类分析确定的每个子类内最重要的一个指标，实现指标集信息重叠程度的降低。具体而言，这类方法首先通过R型聚类分析将指标集划分为若干个不同的子类，属于不同子类的指标间相关程度比较低，而同一子类内的指标间相关程度比较高。在此基础上，仅保留每个子类内最重要的一个指标，剔除子类内其余全部指标，从而实现评价指标集信息重叠程度的降低。如顾雪松等[18]通过剔除R型聚类后各子类内因子载荷最小的指标，对科技评价指标进行了筛选。周立斌等[19]、赵宇哲等[20]通过仅保留R型聚类后各子类内变异系数最大的指标，分别建立了人的全面发展及生态港口评价指标体系。而Chen Honghai等[21]通过剔除R型聚类后各子类内近似分类质量系数小的指标，对城市绿色发展指标进行了筛选。

现有信息重叠指标筛选方法在降低指标集信息重叠方面虽进行了有益的探索，但仍然存在着一些亟待解决的问题。这些问题主要体现在以下四个方面。

已有研究存在的问题一：已有研究[11-17]仅仅剔除相关程度高的任意两个指标中相对不重要的一个指标，难以保证被删除的指标恰是对指标集整体信息重叠贡献大的指标，极易误删对指标集整体信息重叠贡献小的指标，或错误地保留对指标集整体信息重叠贡献大的指标。评价指标集作为一个系统，指标集内各指标彼此之间的相互影响、相互作用是错综复杂的。一个指标与指标集内某个指标间的相关程度高，不意味着该指标与其余全部指标整体间的信息重叠程度也高；同样地，一个指标与指标集内某个指标间的相关程度低，也并不意味着该指标与其余全部指标整体间的信息重叠程度也低。因此，已有研究[11-17]降低指标集信息重叠的方式并不合理。

已有研究存在的问题二：已有研究[18-21]通过保留每个子类内最重要的一个指标降低指标集的整体信息重叠，仅能保证被保留的指标与不同子类内指标间的相关性低，却无法保证保留的指标与指标集内其余全部指标间的整体相关性也低。同时，一个指标与同一子类内其余指标相关性较高，也不意味着该指标与指标集内其余全部指标间的相关程度也高。显然，在降低指标集信息重叠时应该优先剔除与指标集内其余全部指标相关程度高，即应该优先剔除对指标集整体信息重叠贡献大的指标。显而易见，已有研究[18-21]这种指标筛选方法并不能有效地降低指标集的整体信息重叠。

已有研究存在的问题三：已有研究[11-21]虽然能够在一定程度上降低指标集的信息重叠，但是却无法判断剩余评价指标间的整体信息重叠程度是否已经较低，是否还有必要进一步遴选指标。相对而言，剔除指标集内指标的数量越多，剩余指标间整体信息重叠程度也会越低，但评价信息的全面性也会相对越差；相应地，指标集内指标剔除得越少，剩余指标间整体信息重叠程度越高，但综合评价时反映信息的全面性也会越好。因此，指标遴选应适可而止，否则极易造成指标筛选的过度或不足。但显然已有研究[11-21]并不能做到这一点。

已有研究存在的问题四：已有研究[11-21]虽然能够降低指标集的信息重叠水平，但却无法检验其合理性，亦无法比较不同信息重叠指标筛选方法的优劣。

针对上述问题，本研究聚焦于指标集整体信息重叠程度的有效降低，提出了一种基于病态指数循环分析的信息重叠指标筛选方法。首先，以剔除一个指标后指标集病态指数的减小幅度表示该指标对指标集整体信息重叠贡献的大小，循环剔除对剩余指标整体信息重叠贡献最大的指标，实现指标集整体信息重叠的高效降低，克服上述已有研究的前3项不足。之后，通过剔除相关程度高的任意两个指标中相对不重要的一个指标，避免评价指标间整体信息重叠程度不高但少部分指标间信息重叠依然较高。此外，提出指标集整体信息重叠降低效率的概念，通过对比本文方法与已有研究方法的整体信息重叠降低效率，检验本研究所提出的信息重叠指标筛选方法的合理性。最后，以一组科技评价指标的筛选为例，说明本研究所提出的信息重叠指标筛选方法的可行性及有效性。

2 指标筛选原理

如上文所述，信息重叠指标的筛选是在剔除重要性差的指标后进行的。因此，这里假设在利用本文方法筛选指标前已经剔除了重要性较差的指标。

2.1 信息重叠指标筛选的难点

通过上文的分析不难得出信息重叠指标筛选的难点主要有三。

一是如何测度一组指标的整体信息重叠水平？目前，已有信息重叠指标筛选方法均未能实现指标集整体信息重叠水平的测度。这样，在指标筛选过程中无法确定剩余指标的整体信息重叠水平，极易导致指标筛选的过度或不足。

二是如何高效率地降低一组指标间的整体信息重叠水平？已有研究在降低指标集整体信息重叠时仅仅局限于部分指标之间，必然难以高效率地降低指标集整体上的信息重叠。因此，如何在剔除指标数量较少(即评价信息损失较少)的情况下，快速降低指标集的整体信息重叠水平，是一个亟待解决的难题。

三是如何衡量一种信息重叠指标遴选方法的优劣？如果有衡量信息重叠指标遴选方法优劣的标准，就可以实现不同信息重叠指标筛选方法的择优。但遗憾的是，目前已有研究中尚没有此类标准。

2.2 信息重叠指标筛选的基本思路

(1)以病态指数表示指标集整体的信息重叠

在计量经济学理论中，测度变量间多重共线性水平的病态指数越大，越说明该组变量的多重共线性水平越高。不难理解，综合评价中常被提及的“信息重叠”与多元回归模型中的“共线性”意义相同，仅是应用背景不同而已。据此，本文以评价指标集病态指数的大小表示指标集整体的信息重叠程度，解决已有信息重叠指标筛选方法无法测度指标集整体信息重叠程度的不足。显然，指标集的病态指数越小，指标集的整体信息重叠水平越低。从而，难点一得以解决。

(2)确定指标对指标集整体信息重叠的贡献

据上文可知，病态指数可以表示指标集的整体信息重叠程度。而一个指标Xi与指标集内其余指标间存在着一定的信息重叠。自然，从指标集内剔除指标Xi后，指标Xi与原指标集内其余指标间存在的信息重叠在新指标集中便不复存在。从而，不难理解从指标集内剔除一个指标Xi后，该指标集病态指数必然减小，即指标集的整体信息重叠水平必然降低。同时，显然从指标集内剔除一个指标Xi后指标集病态指数减小的幅度，就是指标Xi与指标集内其余全部指标间的整体信息重叠程度。它反映了指标Xi对原指标集整体信息重叠贡献的大小，这里称其为指标Xi的整体信息重叠贡献度。

(3)信息重叠指标的筛选标准

根据整体信息重叠贡献度的定义，不难理解一个指标的整体信息重叠贡献度越大，该指标与指标集内其余全部指标间的整体信息重叠程度越高，该指标对其所在指标集整体信息重叠的贡献越大，剔除该指标后指标集整体信息重叠下降得就越快，该指标越应予以剔除；反之，一个指标的整体信息重叠贡献度越小，该指标对其所在指标集整体信息重叠的贡献越小，剔除该指标后指标集的整体信息重叠下降得越慢，该指标越应予以保留。这便是基于整体信息重叠贡献度的信息重叠指标筛选标准。

(4)基于病态指数循环分析筛选信息重叠指标

假设初始指标集共有n个指标X1,X2,…,Xn，且对综合评价结果而言均比较重要。将这n个指标的病态指数CIn与剔除指标Xi(1≤i≤n)后剩余n-1个指标的病态指数CI(n-1)i的差值CIn-CI(n-1)i，称为指标Xi的整体信息重叠贡献度。

假设在n个指标X1,X2,…,Xn中指标Xi的整体信息重叠贡献度最大，则说明如果从初始的n个指标中剔除指标Xi，则指标集整体信息重叠程度下降的幅度最大。因此，根据基于整体信息重叠贡献度的信息重叠指标筛选标准，应首先剔除指标Xi。我们称这一过程为信息重叠指标的第1轮筛选。这样，指标集内就剩余了n-1个指标。类似地，再剔除剩余的这n-1个指标中信息重叠贡献度最大的一个指标。称这一过程为信息重叠指标的第2轮筛选。依此类推，循环往复，直至剩余指标集的信息重叠程度已经不高为止，解决难点二。计量经济学理论通常认为，如果一组指标的病态指数不大于10，则该组指标的多重共线性就已不高[22]。因此，这里就以剩余全部指标的病态指数不大于10，作为信息重叠指标循环筛选的停止条件。

由于逐轮次地筛选指标的过程中指标集内指标的数量是在递减的，因此不同指标的整体信息重叠贡献度仅在同一轮次内的指标集内可以比较，而不同轮次互异指标的整体信息重叠贡献度不具比较意义。

(5)基于相关性分析进一步筛选信息重叠指标

基于相关性分析进一步筛选信息重叠指标的原因。就指标集整体信息重叠而言，通过上述逐轮剔除整体信息重叠贡献度最大的指标就已经基本完成了降低指标集信息重叠的任务。这与计量经济学中主要着眼于解释变量整体去考虑多重共线性本质上是一致的。但指标集整体信息重叠水平低，并不意味着个别指标间信息重叠也都会低，个别指标间可能存在的较高的信息重叠亦会对综合评价结果造成负面影响。因此，有必要进一步降低个别指标间较高的信息重叠。

基于相关性分析进一步筛选信息重叠指标的思路。这里，借鉴已有研究最常采用的降低个别指标间信息重叠的思路，即剔除任意两个相关性高的指标中相对不重要的一个指标。那么如何衡量指标的相对重要性呢？这里的重要性是指指标对综合评价结果影响的相对大小。众所周知，变异系数(Coefficient of Variance)是衡量指标观测值变异程度的一个统计量。与其它衡量指标观测值变异程度相比，变异系数不受不同指标单位或均值差异的影响，更能简便客观地反映不同指标间相对变异程度的差异。而综合评价理论认为如果一个指标的变异程度不大，则该指标对综合评价结果的影响也不大[23]。正因为此，变异系数成为目前最为常用的一种表示指标相对重要性的统计量。有鉴于此，我们就通过剔除Person相关系数绝对值大的任意两个指标中变异系数相对较小的一个指标，实现个别指标间信息重叠水平的降低。

需要说明的是，剔除整体信息重叠贡献度大的指标应优先于基于相关分析剔除信息重叠指标。信息重叠指标剔除的主要目的在于降低指标集的整体信息重叠水平，避免指标间的重叠信息扭曲综合评价结果。而一个指标的信息重叠贡献度反映的是该指标与指标集内其余全部指标间的整体信息重叠程度，但Person相关系数却仅能反映某两个指标间的信息重叠水平。显然，将指标集的整体信息重叠降低到同一较低的水平，基于相关性分析比基于整体信息重叠贡献度需要删除更多的评价指标才能实现，而这却不利于保持评价信息的全面性。因此，为了保留更丰富的评价信息，应该选择先基于整体信息重叠贡献度快速降低指标集的整体信息重叠水平，再利用相关性分析降低个别指标间的信息重叠水平。下文应用实例通过对比两者信息重叠降低效率(表5)，进一步验证了优先剔除整体信息重叠贡献度大的指标更能快速实现指标集整体信息重叠水平的降低这一结论。同时，通过信息重叠指标的筛选虽能降低评价指标间的信息重叠，但同时也会因评价指标的减少导致评价信息全面性的减弱。因此，在筛选信息重叠指标时应注意权衡指标剔除的数量与评价信息全面性间的关系，避免信息重叠指标遴选的过度或不足。

(6)信息重叠指标筛选方法合理性的检验

为了检验本研究所提出信息重叠指标遴选方法的合理性，我们以指标集病态指数的减小比例与剔除指标数量的比值，即以平均每剔除一个指标后指标集病态指数减小的比例，表示信息重叠指标筛选方法降低指标集整体信息重叠的效率，简称为整体信息重叠降低效率。显然，指标集的整体信息重叠降低效率越大，平均每剔除一个指标后指标集的整体信息重叠下降的幅度越大，这个信息重叠指标筛选方法越合理。这便是基于整体信息重叠降低效率的信息重叠指标筛选方法合理性检验标准。从而，难点三亦得以解决。据此，通过横向比较本文方法与已有方法的整体信息重叠降低效率，体现本研究方法的优势，进而实现本研究方法合理性的检验。当然，这种合理性是一种相对的合理性。

确定整体信息重叠降低效率时除以剔除指标数量的原因：如果确定整体信息重叠降低效率时不除以剔除指标的数量，则仅能在剔除指标数量相同情况下比较不同信息重叠指标筛选方法的整体信息重叠降低效率。而如果确定整体信息重叠降低效率时除以剔除指标的数量，则即使剔除指标数量不相同，仍可比较不同信息重叠指标筛选方法的整体信息重叠降低效率。

综上，本文方法可广泛应用于一般综合评价问题，以降低评价指标间的信息重叠，减弱指标间信息重叠对综合评价结果产生的负面作用，进而构建更加科学合理的评价指标体系。为便于描述，称上述方法为基于病态指数循环分析的信息重叠指标筛选方法，其原理如图1所示。

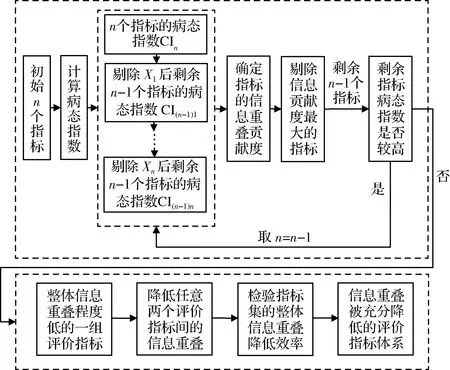
图1 基于病态指数循环分析的指标筛选原理

3 指标筛选模型

为了避免不重要的评价指标在信息重叠指标筛选过程中被保留，假设一组指标X1,X2,…,Xn均是剔除重要性较差的指标后保留下来的。基于病态指数循环分析降低该组指标信息重叠的步骤如下。

(1)基于整体信息重叠降低的指标筛选

步骤1：通过以下特征方程计算矩阵XTX的特征值λ1,λ2,…,λn。

XTX-λjEn=0

(1)

特征方程式(1)中，矩阵XT为指标集对应的样本数据矩阵X的转置矩阵[22]；En为单位矩阵。

步骤2：计算n个评价指标的病态指数CIn[22]。

(2)

病态指数CIn的经济含义：病态指数CIn反映的是指标集X1,X2,…,Xn整体的信息重叠程度，其值越大，越说明这n个指标的整体信息重叠程度越高，对综合评价结果客观性的负面影响也越显著，这n个指标的信息重叠越应予以降低。

步骤3：计算剔除单个指标Xi(i=1, 2, …,n)后剩余n-1个评价指标的病态指数CI(n-1)i。按照上述步骤1-步骤2计算剩余n-1个指标的病态指数CI(n-1)i，不赘述。

步骤4：计算指标Xi(i=1, 2, …,n)的整体信息重叠贡献度Ci1(i=1, 2, …,n)。

Ci1=CIn-CI(n-1)i

(3)

整体信息重叠贡献度Ci1的经济含义：Ci1表示剔除指标Xi后剩余n-1个评价指标的病态指数CI(n-1)i，较之剔除Xi前全部n个评价指标病态指数CIn减小的幅度。其值越大，指标Xi对n个指标的整体信息重叠贡献越大，指标Xi越应被剔除；反之，其值越小，指标Xi对n个指标的整体信息重叠贡献越小，指标Xi越应予以保留。

步骤5：剔除n个指标中整体信息重叠贡献度最大的指标。若

Cj1=max{Ci11≤i≤n}

(4)

则说明在n个指标X1,X2,…,Xn中指标Xj对指标集的整体信息重叠贡献最大，剔除之。

为了描述方便，称上述过程为信息重叠指标的第1轮筛选。类似地，再剔除剩余n-1个指标中整体信息重叠贡献度最大的一个指标。如此循环往复，每轮都剔除剩余指标中整体信息重叠贡献度最大的一个指标，直至满足如下的信息重叠指标筛选的停止条件。

步骤6：信息重叠指标筛选的停止条件。若剩余全部指标的病态指数不大于10，则停止信息重叠指标的筛选。否则，依照上述步骤对剩余指标继续进行信息重叠指标的筛选，循环往复，直至剩余指标集的病态指数已不大于10为止。

(2)基于个别指标间信息重叠降低的指标筛选

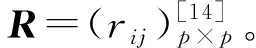
(5)

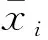
步骤8：计算指标Xi的变异系数[20]CVi(i=1, 2,…,n)。其计算公式为

cvi=

(6)

变异系数cvi的经济含义：变异系数cvi是指标Xi取值的标准差与均值的比值，反映了指标Xi取值的离散程度。而且，变异系数cvi越大，指标Xi相对越重要[20]。

步骤9：基于Person相关分析降低个别指标间较高的信息重叠。即若：

rij>r0

(7)

则剔除指标Xi和Xj中变异系数较小的一个指标，以避免指标集整体信息重叠不高但个别指标间信息重叠程度却依然较高。

式(7)中，r0是信息重叠指标筛选的阈值，通常取一个介于0与1之间较大的值。显然，阈值r0越大，个别指标间的信息重叠降低得越彻底。但与此同时，剔除指标的数量也会越多，损失的评价信息也越多，越不利于综合评价的全面性。因此，阈值r0的大小并无绝对标准，需要权衡确定。这里，取r0=0.7[20]。

(3)信息重叠指标筛选方法合理性检验

步骤10：确定指标集整体信息重叠降低效率ESk。

(8)

整体信息重叠降低效率ESk的经济含义：整体信息重叠降低效率ESk是平均每剔除一个指标后指标集病态指数减小的比例，反映了信息重叠指标筛选后指标集整体信息重叠程度降低的效率。显然，整体信息重叠降低效率ESk越大，信息重叠指标筛选方法越显相对合理。

步骤11：信息重叠指标筛选方法的合理性检验。若

ESk1>ESk2

(9)

则就指标集整体信息重叠降低效率而言，本文方法较之另一种信息重叠指标筛选方法更为合理。

式(9)中，ESk1为本文提出方法的整体信息重叠降低效率，ESk2为另一种信息重叠指标筛选方法的整体信息重叠降低效率。

综上，通过分别降低指标集整体及个别指标间的信息重叠，评价指标间的信息重叠得以系统地降低，以最大限度地减弱信息重叠对综合评价结果产生的负面影响。

4 实例分析

4.1 数据的来源

本文以“R&D人员折合全时当量”、“高新技术增加值占GDP比重”等体现城市科学技术发展水平的10个指标为例，说明本文所提出信息重叠指标筛选方法的可行性及有效性。这10个科技评价指标列于表1第2，4列。这10个指标2000-2013年的统计数据均来源于《大连统计年鉴》，列于表2第2-11列。

表1 实例指标

表2 指标数据

4.2 基于病态指数循环分析的指标筛选

(1)信息重叠指标的第1轮筛选

步骤1：计算由全部10个科技评价指标所构成指标集的病态指数CI10。将表2第2-11列中的数据代入式(1)，得到矩阵XTX的全部10个特征值。再将矩阵XTX的最大特征值5.591及最小特征值0.003代入式(2)，得到10个科技评价指标的病态指数CI10=44.538，列于表3第2列。病态指数CI10远大于10，从而说明这10个科技评价指标整体上存在比较严重的信息重叠，理应予以降低。特征值的计算结果通过基本的线性代数知识即可获得，因此这里不予赘述。

步骤2：计算剔除指标Xi(i=1, 2, …, 10)后剩余9个指标的病态指数CI9i(i=1, 2, …, 10)。将剔除单个指标Xi(i=1, 2, …, 10)后剩余的9个指标作为一个新的指标集，按照步骤1中的计算方式可以分别得到剔除指标Xi(i=1, 2, …, 10)后剩余的9个指标的病态指数CI9i(i=1, 2, …, 10)，依次列于表3第3列。

步骤3：计算指标Xi(i=1, 2, …, 10)的整体信息重叠贡献度Ci1(i=1, 2, …, 10)。将表3第2、3列的CI10及CI9i(i=1, 2, …, 10)的取值分别代入式(3)，得到10个指标各自的整体信息重叠贡献度Ci1(i=1, 2, …, 10)，分别列于表3第4列。

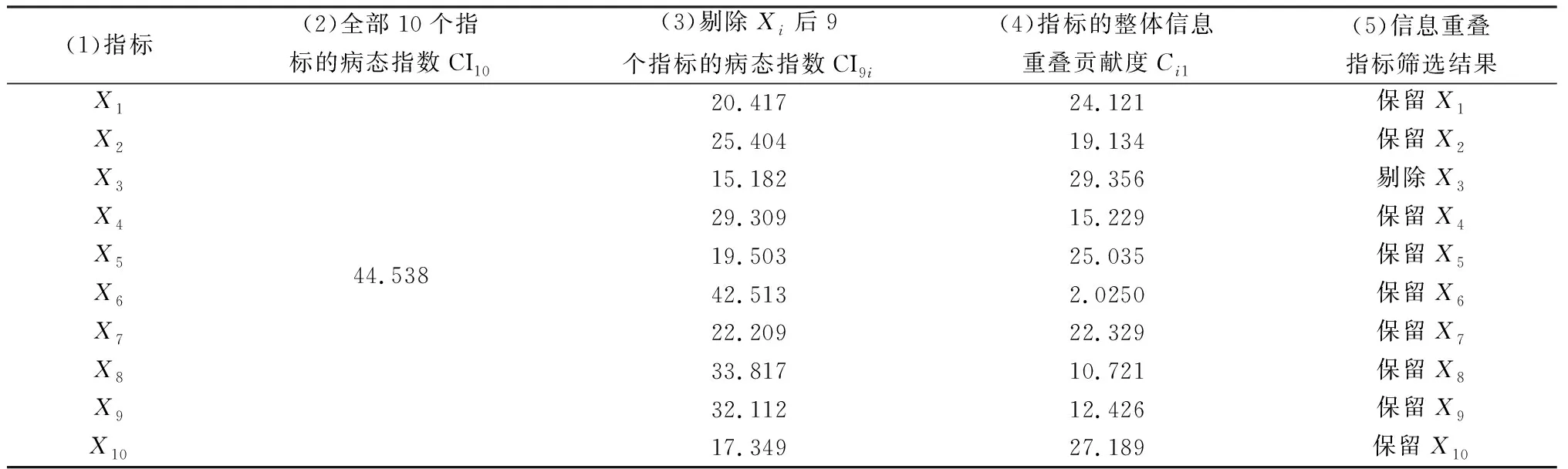
表3 指标的第1轮筛选

步骤4：整体信息重叠贡献度大的指标的剔除。由表3第4列不难发现，指标X3的整体信息重叠贡献度最大，为29.356。即，剔除指标X3后指标集整体信息重叠下降的幅度最大，达到了29.356。因此，应优先剔除指标X3。

步骤5：指标筛选停止条件的符合性检查。据表3第3列第3行可知，剔除指标X3后剩余的9个指标的病态指数为15.182，仍大于10。这说明剔除指标X3后剩余的9个指标间的整体信息重叠水平依然较高，指标集的整体信息重叠水平还需进一步降低。至此，信息重叠指标的第1轮筛选结束。将第1轮指标筛选结果列于表3第5列。

(2)信息重叠指标的第2轮筛选

步骤6：计算剔除剩余9个指标中某个指标后剩余8个指标的病态指数。依第1轮的指标筛选方式，可以类似地得到剔除剩余9个指标中的一个指标后剩余8个指标的病态指数，列于表4第3列。由于第1轮已经将指标X3剔除了，所以表4第3列第3行处以“—”标示。

表4 指标的第2轮筛选

步骤7：计算剔除指标X3后剩余的9个指标各自的整体信息重叠贡献度。再将表4第2、3列的数值分别代入式(3)，得到9个指标各自的整体信息重叠贡献度Ci2(i=1, 2, 4, …, 10)，分别列于表4第4列。

步骤8：第2轮指标筛选中整体信息重叠贡献度最大指标的剔除。由表4第4列不难发现，指标X9的整体信息重叠贡献度是最大的，其值为4.197。因此，剔除指标X9。至此，指标的第2轮筛选结束。

步骤9：再次检查指标筛选停止条件的符合性。据表4第3列第9行可知，累计2轮分别剔除指标X3和X9后剩余8个指标的病态指数为10.985，大于10。这说明剩余的8个指标还存在较为明显的信息重叠，仍然需要通过指标筛选继续降低这8个指标的整体信息重叠。

(3)信息重叠指标的第3轮筛选

步骤10：剔除剩余8个指标中整体信息重叠贡献度最大的指标。类似地，通过第3轮的指标筛选发现在剩余的8个指标中，指标X2的整体信息重叠贡献度最大，为2.000。因此，第3轮的指标筛选应剔除指标X2。而剔除指标X2后剩余7个指标的病态指数为10.985-2.000=8.985，小于10。因此，剩余7个指标的整体信息重叠水平已经不高，指标筛选暂且结束。

综上，通过信息重叠指标的遴选剔除了10个科技评价指标中3个对指标集整体信息重叠贡献最大的指标，即指标X3、X9和X2，暂时保留了其余7个整体信息重叠贡献较小的指标。

(4)降低个别指标间的信息重叠

步骤11：降低相关程度高的两两指标间的信息重叠。将列于表2中被暂时保留的7个指标的数据代入式(5)，容易得到7个指标的Person相关系数矩阵。据式(7)发现，不存在某两个指标间Person相关系数绝对值大于0.7的情况。因此，已无需再降低个别指标间的信息重叠。由此可见，利用病态指数循环分析法筛选信息重叠指标后，指标集不仅整体信息重叠已经较低，而且个别指标间的信息重叠也较低。

综上，本文方法剔除了全部10个科技评价指标中的3个。指标剔除似乎较少，其原因主要有三。一是如上文所述信息重叠指标的筛选是发生在剔除重要性较差的指标后的，因此两种指标筛选方式累计剔除的指标数量自然就会比较多。二是本文方法是在剩余全部指标的信息重叠不高，即剩余全部指标的病态指数不大于阈值10的条件下停止剔除信息重叠程度较高指标的。而决策者若希望评价指标集信息重叠程度更低，或希望评价指标集中指标数量更少一点，则可将本文指标筛选的停止条件中的阈值适度调低一些。因此，即使不结合其它指标筛选方法，仅利用本文方法也可解决待筛指标数量较多的问题。三是信息重叠指标剔除较多会降低评价信息的全面性，不利于综合评价结果的客观合理。因此，信息重叠指标的遴选也应尽量避免评价指标的过度剔除。

4.3 信息重叠指标筛选方法合理性的检验

通过与目前应用最为广泛的Person相关分析法的整体信息重叠降低效率进行对比，验证本文方法的相对合理性。

4.3.1 基于现有相关性分析法的指标筛选

由上文可知，本文方法剔除了3个指标。因此，为了客观对比指标筛选结果，在基于现有的相关分析法(上文模型中的步骤7至步骤9)筛选指标时亦剔除了3个指标，即先后剔除了指标“X9科技进步贡献率”、“X4地方财政科技支出占地方财政一般预算支出比重”和“X2R&D经费支出占GDP比重”等3个指标。

4.3.2 指标集整体信息重叠降低效率的对比

根据上文病态指数的计算方法可以得到全部10个指标的病态指数为44.538，基于Person相关分析法分别剔除1、2、3个指标后剩余指标的病态指数：32.112、23.441及18.238，以及基于相关分析法分别剔除1、2、3个指标后指标集整体信息重叠(病态指数)降低的比例，列于表5第5列。再据式(8)，以表5第5列的数值分别除以表5第2列相对应的剔除指标的数量，得到基于相关性分析法分别剔除1、2、3个指标后指标集整体信息重叠降低的效率，列于表5第6列。

表5 信息重叠降低效率的比较

类似地，根据上文实证数据得到本文方法分别剔除1、2、3个指标后的指标集整体信息重叠降低的比例及效率，依次列于表5第3-4列。再将表5第4列与表5第6列同行数据的差值，分别除以表5第6列同行的数据，得到两种方法指标集整体信息重叠降低效率的相对差距，列于表5第7列。以表5第7列第2行的“73.67%”为例，它是表5第2行中第4列的“37.67%”与第6列的“21.69%”的差值，再除以表5第6列的“21.69%”得到的。它表示同样是剔除2个指标，本文方法的指标集整体信息重叠降低效率，比现有相关性分析法相对地高73.67%。

综上，不难发现本文方法比现有基于Person相关分析的指标筛选方法，在降低指标集信息重叠方面优势十分显著。具体而言，优势有三：

(1)本文方法降低指标集信息重叠的效率更高

据表5第7列可知，就指标集整体信息重叠降低效率而言，在剔除指标个数均分别为1、2、3的情况下，本文方法比已有最常用的Person相关分析法分别高136.24%、73.67%和35.21%。因此，与现有最常用的相关性信息重叠指标筛选方法相比，本文方法降低指标集整体信息重叠的效率要高的多。

(2)现有方法易误删对信息重叠贡献小的指标

据上文指标筛选过程可知，指标X4并不是对指标集信息重叠贡献最大的3个指标之一。而现有Person相关分析法却在剔除第2个指标时就剔除了指标X4。这意味着基于Person相关分析的信息重叠指标筛选方法误删了对指标集整体信息重叠贡献较小的指标X4。而对指标集整体信息重叠贡献较小的指标是应该予以保留的。

(3)现有方法易保留对信息重叠贡献大的指标

据表3第3列可知，指标X3是初始的10个指标中整体信息重叠贡献度最大的指标。而对指标集整体信息重叠贡献越大的指标，越应予以剔除。显然，在指标筛选过程中指标X3理应被第1个剔除。但现有Person相关分析法保留了指标X3。因此，Person相关分析法容易错误保留对指标集整体信息重叠贡献大的指标。

综上，不难理解的是，正是由于现有Person相关分析法容易误删整体信息重叠贡献小的指标，及容易错误保留整体信息重叠贡献大的指标，才导致了该方法降低指标集整体信息重叠的效率明显偏低。而本文方法总是优先剔除指标集中整体信息重叠贡献最大的指标，并不存在容易误删对整体信息重叠贡献小的指标或容易错误保留对整体信息重叠贡献大的指标的弊端。

5 结语

本研究聚焦于评价指标间信息重叠程度的有效降低，提出了一种基于病态指数循环分析的信息重叠指标筛选方法。通过逐轮剔除指标集中整体信息重叠贡献度最大的指标，直至指标集整体信息重叠较低为止，实现了指标集整体信息重叠程度的快速降低。在此基础上，通过剔除Person相关系数较高的任意两个指标中变异系数较小的一个指标，避免指标集整体信息重叠不高但个别指标间的信息重叠却依然较高。从而较为系统地实现了评价指标间信息重叠水平的降低，最大限度地降低了指标间的信息重叠对综合评价的负面影响。最后，提出通过指标集整体信息重叠降低效率检验信息重叠指标筛选合理性的方法，实现了即使在剔除指标数量不同的条件下亦可比较不同方法降低指标集整体信息重叠效率的高低。

本研究提出的信息重叠指标遴选方法适用于评价指标体系的构建，即适用于在剔除重要性较差的指标后，进一步系统地降低剩余指标间的信息重叠水平。特别是，对于个别或部分指标间的相关程度较低而指标间整体信息重叠水平却较高这一情形，尤为适用。

本研究仅聚焦于指标集信息重叠的降低，因此同其它信息重叠指标筛选方法一样，还需要与以剔除重要性差的指标为目的的指标筛选方法结合使用，才能系统实现综合评价指标的筛选。此外，本研究虽通过指标集整体信息重叠降低效率实现了信息重叠指标筛选方法的合理性检验，但却需要与现有方法横向比较整体信息重叠降低效率才可实现信息重叠指标筛选方法的合理性检验。这些都是需要在今后的研究中进一步加以完善的。