一种基于Laplacian的半监督特征选择模型
2019-03-04吴锦华万家山霍清华
吴锦华 万家山 伍 祥 霍清华
(安徽信息工程学院计算机与软件工程学院, 安徽 芜湖 241000)
在机器学习和模式识别领域,传统学习算法在处理高维数据(如生物特征数据、基因数据、股票交易数据、社交网络数据)时容易遭遇“维数灾难”问题,即计算量随着维数(特征的数量)的增加而呈指数倍增长。目前的降维技术可分为2类:一类偏向于高维数据的有效表示,如特征选择、特征提取、稀疏表示等方法;另一种偏向于构建学习模型,如分类回归模型、聚类模型等。各种特征选择方法都有各自一定的优势,同时也存在一定的不足。本次研究,将提供一种同时引入LASSO稀疏项和Laplacian正则项的半监督学习特征选择模型。
1 LASSO法及其扩展模型
特征选择方法的目的在于从高维数据中提取有效表示形式,从而为目标学习模型提供帮助。具有代表性的特征选择方法有拉普拉斯积分(LS)、递归特征消除(RFE)、顺序向前移动选择(SFFS)、Fisher Score(FS)和套索算法(LASSO)等。基于稀疏理论的特征选择方法得到了较多的关注,比如LASSO方法。LASSO模型[1]引入的稀疏项保证有价值的特征能被选择,并且所选特征具有很强的可解释性,但它在处理高维数据时计算速度比较慢。基于LASSO方法,有人提出了Fussed Lasso方法[2],可优化计算速度;有人引入流形正则项,提出了一种基于流形正则化的多任务特征选择方法(M2TFS)[3];有人引入判别性正则化项,提出了判别性特征选择方法[4];有人为解决非线性问题,在LASSO方法基础上引入了核函数[5]。另外,Conrad等人提出了一种稀疏蛋白质组分析算法(SPA)[6]。这些方法都是利用稀疏理论的相关知识来进行数据降维,但在线性映射过程中往往忽略了一些有用的样本结构信息。
实际应用中,通常出现大量的无标签样本,而有标签样本不易获取。如医学图形图像数据、基因数据等,都需要人工对其进行分类。因此,半监督学习技术备受关注,半监督方法可利用少量的标签信息而获得较好的方法模型。Jie Biao等人在M2TFS模型的基础上提出半监督模型semi-M2TFS[7],并将其用于脑网络数据分析,对参数具有很强的鲁棒性。严菲等人提出了基于局部判别约束的半监督特征选择模型[8],充分利用已标记样本和未标记样本训练特征选择模型,并借助相邻数据间的局部判别信息,提高了模型的准确度。奚臣等人结合流形正则化框架,提出了一种流形与成对约束联合正则半监督分类方法[9]。叶婷婷等人提出的基于有效距离的多模态特征选择模型[10],也在于充分利用样本数据之间的结构分布信息。
近年来,随着正则化、稀疏化理论以及半监督模型的发展,相关技术已广泛应用于数据降维。基于前人的研究成果,本次研究将提供一种半监督拉普拉斯特征选择模型(semi-supervised laplacian feature selection,缩写为“SLFS”)。基本思路是:利用LASSO方法中的稀疏项,去除冗余特征;构建Laplacian正则化项,保存样本分布信息;通过重定义近似矩阵来构建半监督特征选择模型。
2 SLFS模型的建立
2.1 LASSO算法
LASSO方法最早是由Robert Tibshirani提出的,可将其简单刻画如下。
X=[x1,x2,…,xN]∈Rd×N
Y=[y1,y2,…,yN]∈RN
其中,X为给定的训练样本集;N表示样本的数量;xi表示样本X中的第i个特征向量;d为样本特征维数;Y表示类标签向量。在全监督分类问题中,yi表示Y中第i个样本的类标签,其值可以为离散值或具体数值。为方便数据处理,我们仅考虑2类分类问题,因此,yi∈{-1,+1}。
通常情况下,LASSO方法优化的目标函数如下:
(1)
其中,w表示特征向量的回归系数,维数为d。正则项‖w‖1为L1范式,用于在高维特征空间中产生稀疏特征解。如果wi=0,则表示对应的特征冗余;wi≠0,则为样本的有效特征,可用于后续的分类。λ是正则项的参数(λ>0),主要用于平衡模型复杂度和数据拟合程度之间的相对贡献,其值通常可以通过交叉验证的方法来获取。
2.2 引入Laplacian正则化项
在LASSO及其扩展模型中,一般采用线性函数即f(x)=xTW=WTx,将原始数据从高维映射到一维。这仅仅反映了样本和对应标签之间的关联关系,忽略了样本数据之间的内在关联信息。为了解决这个问题,引入Laplacian正则化项,保存样本间几何分布信息。同种类型样本经过投影后会产生比较大的偏差,但通常情况下,2个样本如果为同一个类,那它们应该靠得更近。
(2)

2.3 构建近似矩阵
为充分利用无标签样本,并反映其内在的几何分布信息,首先定义对角矩阵P∈RN*N,用于标出有标签数据和无标签数据。如果样本i的标签是已知的,则Pii=1;否则,Pii=0。
采用式(3)定义近似矩阵:
Sij=exp(-dist(xi,xj)t)
(3)
其中,t为经验参数,可以根据经验来选取。
dist(xi,xj)=‖xi-xj‖2
如果2个样本xi和xj来自于同一个类,那么其经过映射后的距离就更小;如果来自于不同类,那么它们之间的距离就会更大。
2.4 设立目标函数
在某种意义上,Laplacian正则化项主要保存同类样本数据之间的特征空间分布信息,而该分布信息可以提高模型的分类性能[3],且无标签样本更易获取。因此,以式(4)为半监督特征选择模型的目标函数。
(4)
式中:l和b为调谐参数(l>0,b>0),主要用于平衡稀疏项和Laplacian正则项之间的相对贡献度,其值可在训练数据时通过交叉验证的方法来确定;L是根据式(3)重新刻画的Laplacian矩阵。
需要注意的是:式(4)的第一部分(即加下划线部分)只利用有标签数据进行有监督学习;而重新构建的正则项利用数据集中所包含的无标签和有标签数据,保存了原始数据的相邻几何分布信息,用于产生更具判别力的特征。如果使用的样本全部为有标签样本,且b=0,则模型退化为LASSO;如果全部采用有标签样本,则模型退化为Lap-LASSO[11]。
在模型中,引入的LASSO稀疏项的主要作用是选择少量有效特征;重构的Laplacian正则项用于保留同类有标签和无标签样本内在的几何分布信息,从而帮助模型选出更具有判别能力的特征集,为后续分类器提供最有效特征。
2.5 优化算法
采用加速近似梯度(APG)来优化所提出的方法模型。
首先,将目标函数划分为平滑部分和非平滑部分。
平滑部分:
(5)
非平滑部分:
g(w)=λ‖w‖1
(6)
其次,构造函数Ωl,对式(5)和式(6)求近似解。
Ωl(w,wk)=f(wk)+[w-wk,▽f(wk)]+
(7)
式(7)中,▽f(wk)为第k次迭代的wk点的梯度;l为步长,其值可以通过线性搜索的方式来确定。对APG中w的更新步骤定义如下:
(8)
其中
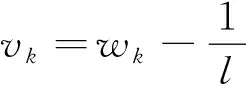
根据式(8)求解优化的问题可以划分成d个单独的子问题,这些子问题的解容易求取[12]。即
(9)
另外,根据文献[12]使用的方法,计算搜索点如公式(10),用其代替在wi上的梯度下降。
Qi=wk-αi(wi-wi-1)
(10)
其中
3 模型试验
3.1 试验数据集
为了检验方法的有效性,用5个数据集(见表1)对模型进行验证。试验过程中,将数据集分成2个部分,一部分被作为有标签数据,另一部分作为无标签数据。
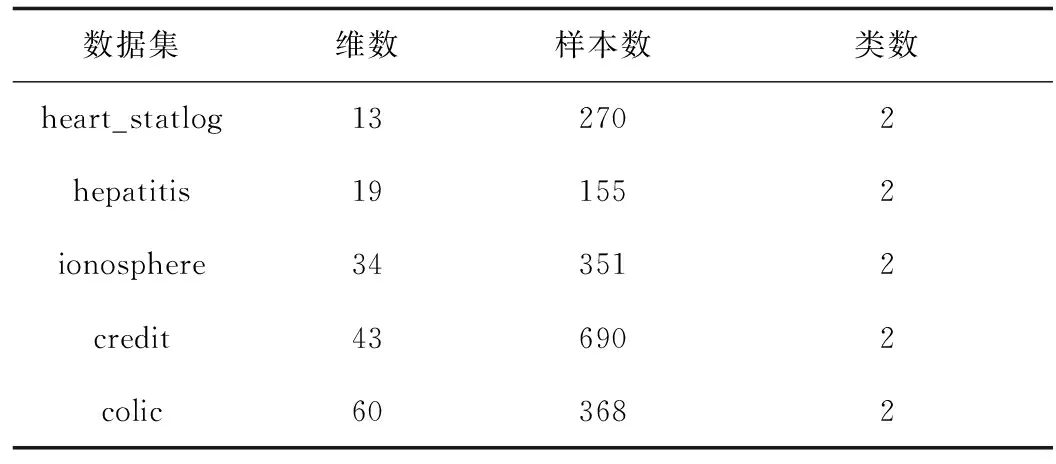
表1 试验数据集描述
3.2 试验方式及结果评价
对模型的性能分别从2个方面来评价[3]:(1)在使用和不使用无标签数据情况下,模型的分类性能表现;(2)固定有标签数据的占比,使用不同数量的无标签数据时,模型的分类性能表现。
在第一阶段试验中,固定50%的样本为有标签数据,其余的作为无标签数据,进行十折交叉验证。将有标签数据划分为10等份,在每次交叉验证中,将90%的有标签数据和所有无标签数据用于模型训练,剩余10%的有标签数据用于模型性能测试。试验重复10次,主要目的是避免样本的随机划分而导致结果偏差。比较试验结果与传统全监督模型的分类结果(见表2),可以看出,在所有数据上,所提方法的分类精度都要高于参与比较的其他方法,说明SLFS特征选择方法更能改进分类性能。

表2 不同方法的分类结果
在第二阶段试验中,测试模型在不同数量的无标签数据上的分类性能。固定50%的样本作为有标签样本,然后在剩下的样本中依次选择10%、20%、40%、60%、80%、100%的样本作为无标签样本,进行十折交叉验证。根据试验结果,绘制了模型的分类精度变化曲线,如图1所示。

图1 无标签数据量与模型分类精度的关系
试验结果显示,在5个UCI数据集的分类上,随着无标签数据数量的增加,分类精度能一致得到提升。由此可见,充分利用样本数据中的几何分布信息,有助于选出更具判别力的特征。
4 结 语
在处理高维数据时,为了克服“维数灾难”问题,LASSO及其扩展模型主要是采用线性函数来将原始数据从高维映射到一维。这样做,可以反映样本和对应标签之间的关联关系,但忽略了样本数据之间的内在关联信息。为充分利用无标签样本,反映其内在的几何分布信息,我们提出了基于Laplacian半监督的特征选择模型。通过引入Laplacian正则化项来保存样本分布信息,可以帮助获得更具判别力的特征。在UCI数据集上的分类试验结果表明,这种方法能有效提高分类性能,而样本的几何分布信息是不应该被忽略的。
