基于k-ε湍流模型的结构物水流中跌落过程数值分析

王永虎， 林天龙

(1. 重庆交通大学 航空学院，重庆 400074; 2. 中国民航飞行学院 飞行技术学院，四川 广汉618307)

0 引 言

目前结构物在水中跌落问题的研究涉及到许多领域，如水下航行器入水、失事船舶或航空器碎片水中跌落、深弹水下弹道等。结构物在水中跌落是连续的，水中的环境比较复杂，其轨迹很难准确预测。在2014年3月发生的马航MH370失踪事件中，为了搜寻坠毁的残骸，马来西亚政府及世界各国耗费相当大的财力和资源。然而海洋环境相当复杂并且瞬息万变，直至2017年1月，马来西亚政府不得已宣布对失踪的MH370客机进行搜查。此次失败的搜查结果也印证了结构物在跌入洋流之后，其真实的运动轨迹是难以人为预测的。物体跌落到水中会导致复杂的流体现象[1-2]，扰动也会对物体造成冲击载荷，从而改变了物体的运动轨迹。针对物体在水中跌落现象的研究有很长的历史[3]。K. T. HOLLAND[4]等在水中运动实验中观察到，当参数不一的圆柱体在体心、重心、方向以及下降路径等情况相同时，向重心的偏移致使物体发生竖直方向的变化等诸多复杂的实验现象。许多学者致力于圆柱体自由跌落到水中的现象研究，未考虑到水流的影响[5-6]。A. V. ABELEV等[7]做了大量的关于全比圆柱体的实验，同时对流体力学的特性进行了进一步的研究和争论。J. MANN等[8]建立计算模型来预测圆柱状的鱼雷机体撞击水表面和跌落到海底的水中运动情况。M. HOROBITZ等[9]对结构物(主要为圆柱体)在只受重力状况下，其入、出水方面动力学进行了更加深入的探究。陈宇翔[10]等用VOF方法对圆柱体入水进行了二维模拟仿真并与实验对比，讨论流体粘性的影响。屈秋林[11]等采用整体动网格法和VOF方法模拟分析飞机水上迫降情况。总之，针对物体在静止水中跌落的研究较多，而对运动水流情况下的结构物水中跌落问题研究较少。

主要通过ANSYS FLUENT软件对圆柱体在有水流的水中跌落进行三维模拟仿真，采用了可实现的模型的湍流模型，运用了动网格和六自由度模型对圆柱体与水面相对运动进行有效处理；同时采用VOF对自由液面附近的变化进行了较好的捕捉，对水中的运动进行了较好的模拟；通过对整个跌落过程进行模拟，重点针对水流跌落轨迹进行了详细分析。

1 问题描述

水流中跌落试验装置示意图如图1。

试验对象为圆柱体，具体参数如表1。实验水池的长宽高为2.0 m×0.60 m×0.60 m，水流速度为0.1 m/s，结构物入水时的初始速度设置为0.5 m/s。采用电磁铁控制夹具是否分离的方式，使圆柱体在12.739 mm的高度下以自由落体方式，落进实验水池内。利用高速摄像机，准确清晰地将圆柱体落水时的运动轨迹和现象完整的记录下来。

图1 跌落实验示意Fig. 1 Sketch of falling experiment

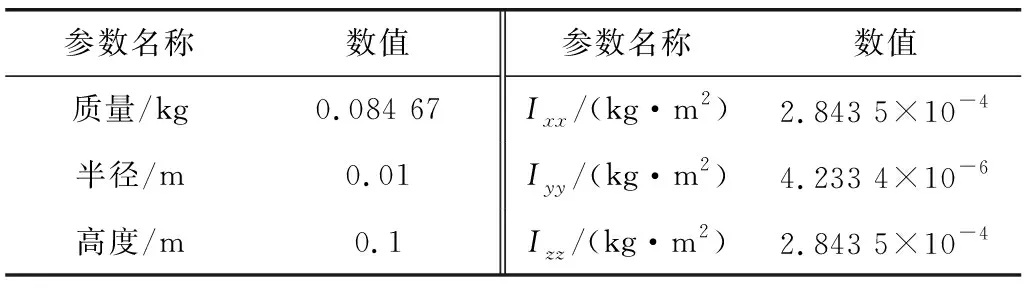
参数名称数值参数名称数值质量/kg0.084 67Ixx/(kg·m2)2.843 5×10-4半径/m0.01Iyy/(kg·m2)4.233 4×10-6高度/m 0.1Izz/(kg·m2)2.843 5×10-4

采用ICEM CFD16.0建立长宽高为0.2 m×0.16 m×0.25 m的三维数值实验水池。非结构四面体网格作为数值模型的整体网格的基础网格，结构物入水跌落轨迹作为实验的侧重点。为了提高实验效率，对圆柱体周围和气液交界面用进一步加密的密度盒网格，而在结构物撞击区之外的区域(也就是流固耦合区域)，采用粗网格的方式进行实验。为了模拟使得水流速度恒定，将流速为0.1 m/s的速度入口作为水流入口的边界条件，将压力出口作为出口水流的边界条件，数值水池的上下面的入口边界条件设为速度值为0，其余边界条件均设为对称边界条件。

2 软件介绍、理论基础和计算方法

结构物水中跌落涉及流固耦合和多相流等方面问题。结构物从空气中进入水中并在水中运动会改变流场、速度和压强场等，并且结构物运动会随水流的运动而改变。圆柱体水中跌落现象复杂，不仅仅受到重力和浮力，还受到湍流阻力和水流推力等的影响。使用VOF方法[12]对自由表面进行捕捉，且修改边界条件，打开明渠模型，用来制造水流。采用了可实现的k-ε模型的湍流模型，运用了有限体积法求解方程。有限体积法是CFD中比较成熟的一种运算方法。笔者将三维圆柱体视为刚体进行运算。三维圆柱体自由落体跌落到水中，并在水中下落是一个复杂的过程。笔者采用了六自由度动网格技术对圆柱体运行进行分析，并对其运动位置进行记录。

2.1 FLUENT软件介绍

ANSYS FLUENT是一款模拟流场、热传递和化学反应比较成熟的CFD软件。在采用非结构网格处理复杂模型时，FLUENT用其完整的网格适应性来解决采用非结构网格的流体问题。FLUENT支持的网格类型主要为二维网格(三角形与四边形网格)、三维网格(四面体、六面体、棱柱等多面体)和混合网格，并且能够根据具体情况细化或加粗网格。

2.2 控制方程

拉格朗日有限体积分析的质量守恒方程：

(1)

式中：ρ为密度；t为时间；u、v和w为物体x、y和z方向的速度。

动量守恒方程为：

(2)

(3)

因为入水和水中跌落问题几乎不考虑热量交换等热力学问题，所以只采用质量守恒方程和动量守恒方程。

2.3 VOF模型

用VOF模型来模拟多相流的方式是先求解一组动量方程，然后在区域内追踪各种流体的体积分数。VOF方程主要适用于两种或两种以上不相容流体。另外一种流体在添加到模型之后，其体积分数也将进入到计算网格中。在任何一个网格中的参数和属性不仅是单一相的代表，也是混合相的代表，其大小主要依赖体积分数。

假设第q种流体体积分数在网格下为αq，αq=0表示网格的第q种流体为空；αq=1表示第q种流体充满网格的条件下，主要包括第q种流体和其他流体。体积分数的离散公式：

(4)

式中：n+1为新时间步长的指数；n为前一时间步长的指数；αq,f为第q个相流体的体积分数面数值；V为网格体积；Uf为以一定速度流经面网格的体积通量。

2.4 明渠模型

水的流速设置通常情形下用明渠模型[13]。实验中为了防止自由液面崩溃现象的发生，在压力出口处调整了自由液面和底部的高度，用压力规范法、密度插值法来处理自由液面。

自由液面ylocal在控制方程中为：

(5)

试验仿真表明，自由液面的边界变化在使用明渠模型后并未出现崩溃的情形，结果如图2。

图2 自由液面变化Fig. 2 Changing diagram of free surface level

2.5 动网格的使用

一般采用动网格来把握流场的运动和追踪边界随时间的变化动态[14]。网格方法选用弹簧近似光顺模型和局部重构模型，其中弹性常数设置为0.5，网格重画方法为局部网格和局部面，打开尺寸函数，其他系数使用默认值，并且打开六自由度模型以便获取圆柱体的重心位移。使用UDF定义圆柱体的质量和转动惯量。

惯性坐标系中，重心移动的运动控制方程为：

(6)

2.6 湍流模型

使用可实现的k-ε模型的湍流模型，可实现的k-ε模型包含湍流黏度的可选择公式，在改良的运输方程中，湍流耗散率ε来自于有关平方涡度波动运输的精确方程。

其运输方程如式(7)、式(8)：

ρε-YM+Sk

(7)

(8)

式中：

(9)

(10)

(11)

式中：Gk为来自于平均速度的梯度湍流动能；Gb为浮力产生的湍流动能；YM为在可压缩流波动的膨胀值；C2与C1ε为常数；σk和σε是k与ε的湍流普朗特数。

2.7 SIMPLEC算法

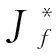
(12)

(13)

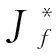
(14)

式中：

(15)

(16)

式中：p′为网格压力修正值。

将通量修正方程(14)、(15)带入方程(12)得到：

(17)

式中：

(18)

2.8 二阶迎风格式

采用二阶迎风格式，其具有较小的扩散性，方程为：

(19)

式中：

(20)

(21)

a+=max(a,0)

(22)

a-=min(a,0)

(23)

为了判断式(19)是否稳定，需满足：

(24)

2.9 计算方法

选用SIMPLC算法求解压力和速度耦合、最小二乘法求解梯度方程、PRESTO!求解压强差值、体积重构求解体积分数，其他均为二阶迎风求解。

3 计算结果及分析

对三维圆柱体在水流中跌落的相关问题，以利用动网格技术与VOF方法相结合方式来进行数值模拟试验，先分析整体阶段，进而深入分析圆柱体水中跌落阶段，将实验与模拟的成果相互对比，最后得出结论。

3.1 整体阶段的速度分析

空中圆柱体只在重力的作用下跌落水中，然后在水中持续运动。在整个过程中圆柱体先受到重力的作用，入水之后逐渐转变为重力、浮力以及水流产生的水动力等复杂的合力，单一力到复杂力的演变过程，致使其各方向的运动速度也随其情况的变动产生变动。

假设将试验物体在刚与水接触时设为0 s，此时速度为0.5 m/s。图3显示了结构物从入水后运动过程的竖直方向速度随跌落水中时间变化而发生的变化。可以观察到物体由于受到流体的浮力以及湍流阻力的影响，在与水面接触后，竖直方向速度变化由平缓逐渐递增；在试验物体完全入水中后，竖直方向的速度仍在增加，随后竖直方向加速度突然增加，然后随时间变化逐渐变得平缓。故物体在整个过程中受力逐渐趋于平稳，且其在水中竖直方向速度的变化对物体水中跌落的轨迹产生重大的影响。

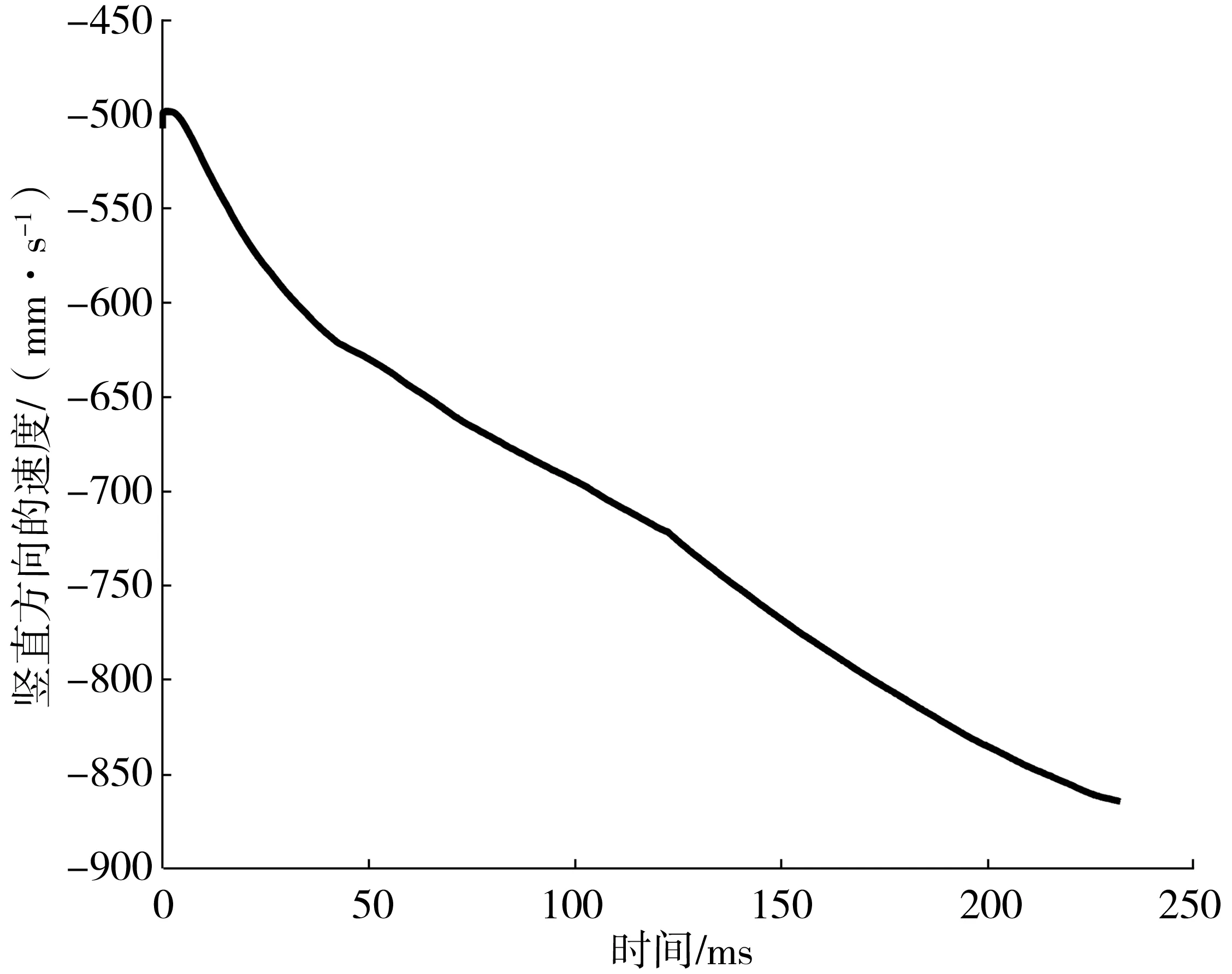
图3 竖直方向速度的时间历程Fig. 3 Vertical velocity time history diagram

图4显示的变化曲线为水平方向速度随时间的变化状况。由于水流的作用，圆柱体刚开始入水时与水的接触面略小，水流作用小，其速度也就越平缓。随着时间推移，在圆柱体全部浸入水中后，逐渐增加的水流作用力使得速度增加变快。当圆柱体水平方向速度约70 mm/s时，水平速度增加变得缓慢，结构物水平方向的位移也在不断地变大。

图4 水平方向速度的时间历程Fig. 4 Horizontal velocity time history diagram

因为结构物密度大于流体的密度，在水流中跌落运动中的速度一直增大，此时会受空穴的影响，使得空泡出现，减小其在水中运动过程受到的阻力。结构物在持续跌落运动中因为气泡发生溃散，圆柱体承受力也随之不断发生变化，甚至发生短暂的震荡。图5展示了结构物水中跌落加速度随时间的变化。在60 ms到70 ms间出现最大加速度时，结构物表面的空穴与其脱离，水流作用力达到最大。随着结构物周围气泡持续破散，随后物体的加速度持续降低，水流作用力逐渐减小，最后趋于平缓。当结构物的水平速度和水流速度相等时，水平方向的位移也呈现出直线的状态。

图5 水平方向加速度的时间历程Fig. 5 Horizontal acceleration time history diagram

3.2 水中跌落阶段分析

圆柱体入水相关的实验研究相当复杂，物体水中跌落运动是研究的重点。笔者主要研究完全入水后结构物跌落轨迹的状况。实验截取了4个典型入水时刻的数值结果和试验结果，具体实验结果如图6。

图6 数值仿真与实验记录图像对比Fig. 6 Comparison of numerical simulation and experimental results

因为流体会粘附在圆柱体的周遭，“空穴”效应和气泡现象就会在其入水的过程中显现出来，如图6。在结构物跌落入水时，周围的气体也一并被压进水里，在55 ms的时候，会有明显的空穴效应显现。圆柱体运动到75 ms时，空穴与圆柱体分开并破散，此时水面出现波动现象。受从右向左的水流速度的影响，在95 ms时，圆柱体周身的气泡在自由液面波浪与圆柱体最初位置关系在水平方向抵消时慢慢减小。对比发现，数值模拟很好演示出圆柱体在水流中跌落的运动过程，同时跌落空化的生成、瓦解等主要的水动力特征也很好的被再现出来。

通过准确的判断结构物落点的区域，分析其水平方向的位移变化，确定其在水底分散情形，更加科学的探究结构物在水流中跌落的运动轨迹。图7展示的是结构物水平方向的位移和时间变化的关系。采用工程偏差及实验值表现方式展现出结果。工程偏差通过总结大量的物体落水运动试验得出。

图7 水平方向位移的时间历程Fig. 7 Horizontal displacement time history diagram

通过采用FLUENT的数值模拟方法对圆柱体在水流中跌落过程进行仿真，仿真结果出现在试验结果工程误差的范围内，符合工程误差的要求，因此仿真结果与试验结果趋于相同。

结构物在水流中下落时，随着水平方向速度的增加，曲线变化率也由明显到渐渐趋于一致，当速度达到0.1 m/s，其速度不再增加，最后曲线渐渐趋于直线。从图7的仿真数据能大致得出每个时间段圆柱体的落点区域范围。

圆柱体水中跌落的运动轨迹见图8。结构物位置被清晰地展示出来，进而确定水流中结构物具体跌落位置的范围，对运动轨迹可以进行明确地分析和预测。

据图8，仿真的运动轨迹和实验结果非常切合，且处于合理误差内。

图8 水平方向与竖直方向位移之间的关系Fig. 8 Relation between horizontal and vertical displacement

通过对圆柱体在实验水流中轨迹进行拟合，可以得出结构物水流中跌落的轨迹方程为：

y=0.091 6x3-1.648 7x2+20.221 3x+4.38

(24)

式(24)虽然只涉及具体情形下圆柱体水中跌落的轨迹方程，但针对跌落速度与来流速度等因素不同状况的结构物水中跌落过程试验可提供借鉴，另一方面也有利于结合相似准则，用于不同的水中跌落情况探究。

4 结 论

为了获得结构物水流中跌落轨迹和散布规律，采用CFD对圆柱体自由落体跌入水中情况进行了数值模拟。采用明渠模型真实捕捉自由液面，利用可实现的k-ε模型来模拟湍流，数值模拟结果与实验结果吻合得较好，符合水动力特征，验证了模型的可行性。研究结果表明，圆柱体在水流中脱离空穴时受水动力较大，影响跌落轨迹和散布落点。通过采集圆柱体重心位置的三维数据，结合误差分析，拟合出水流中跌落轨迹方程，为后续研究不同入水速度和不同流速多工况的结构物水中跌落提供参考依据。