大型民用飞机气动外形典型综合设计方法

2019-03-04黄江涛高正红余婧郑传宇周铸

航空学报 2019年2期

黄江涛，高正红，余婧，郑传宇,*，周铸

1.中国空气动力研究与发展中心计算空气动力研究所，绵阳 621000 2.西北工业大学航空学院，西安 710072

随着高性能计算机与数值模拟技术的飞速发展，数值优化手段开始在飞行器气动外形综合设计中发挥重要作用。与传统“Cut and Try”试凑不同，数值优化设计避免了数字化模型修型、网格划分以及指标转换迭代等繁琐的重复性人工操作，极大程度上减少了设计结果验证需要开展的风洞试验次数，取而代之的是高效率的搜索算法、全自动化的网格重构以及智能决策体系等高效率模块，很大程度上对气动外形设计手段起到变革作用，促进了设计空气动力学的发展，更进一步丰富了气动优化设计的研究内容。

对于客机、运输机、长航时无人机等大型飞机而言，先进的数值优化技术显得尤为重要，尤其是大型民用飞机，气动设计直接关系到飞机的巡航经济性能，对民用飞机市场竞争力产生重要影响。与中小型飞机不同，大型飞机由于机体本身较大的参考面积，一个阻力单位(1 count=1.0×10-4)的减阻效果将带来较为明显的经济效益，因此，大型民用飞机气动设计更趋向于精细化，同时由于安全性等方面的要求，也更加注重于综合性能设计。

精细化、多目标综合设计是大型民用飞机设计的最明显特征，这对传统设计手段提出了挑战，对于新一代远程宽体飞机设计而言，巡航速度更高，在苛刻的设计要求条件下，由此带来的设计难度更大。目前，应用于气动外形综合设计的优化手段主要包含两类：基于非梯度信息类的气动优化(如进化类算法、模式搜索算法等)[1-7]，以及基于梯度信息类的气动优化[8-13]，每种方法均有各自的优缺点，在气动设计领域均得到了一定程度的应用。尤其是基于伴随方程的梯度类优化方法由于其极高的计算效率，倍受CFD工程师、气动设计工程师以及气动优化技术研发人员的关注，也是国内外空气动力学研究机构一个重要的研究方向，且开展了基于伴随方法的综合优化设计，典型有代表性的研究工作有，密歇根大学Lyu等基于离散伴随方法开展了CRM(Common Research Model)外形多点设计[14]，Kenway和Martins基于离散伴随开展了包含抖振特性的多点设计研究[15]。如何有效利用各种方法的优点，实现飞行器气动外形高效率综合优化，对于工程应用来讲，是一个值得探讨的研究方向。

面向气动外形多点综合优化设计问题，本文基于课题组自主研发的飞行器气动外形大规模并行化、分布式综合设计软件AMDEsign(Aircraft Multi-disciplinary DEsign)，结合主分量分析方法，研究了离散伴随方法在典型宽体飞机模型气动设计中应用研究，同时提出了基于“虚拟可行解”的权系数导向选择方式，及其在离散伴随多目标优化设计中应用的可行性，为气动设计人员在优化策略选择上提供一些有价值的参考。

1 AMDEsign飞行器多学科优化设计平台简介

本文的研究基于课题组面向航空航天飞行器自主研发的AMDEsign软件平台进行，该平台是基于并行环境下研发的分布式大型优化设计代码，可以应用于民用飞机、作战飞机、进气道、超声速飞机声爆抑制、旋翼/螺旋桨、高铁减阻设计等航空航天、工业空气动力设计工程领域。主要包含了基本功能、学科分析、伴随体系、传统体系等框架。几个框架由优化决策模块统一管理，其中：

1) 基本功能框架包含了网格重构、参数化建模等共用功能性模块。

2) 学科分析框架主要包含了流场分析、气动弹性、声爆计算、结构分析等学科分析模块。

3) 伴随框架包含了流场伴随、多学科耦合伴随等模块。

4) 传统框架主要包含了试验设计、代理模型等模块。

本文基于平台中的主分量分析、离散伴随系统等模块进行综合设计方法研究。

2 高维目标空间优化问题

民用大飞机气动设计需要综合考虑巡航升阻比、阻力发散、力矩特性以及抖振边界等问题，是典型的高维多目标优化问题。非支配解方法是处理多目标优化比较有效的手段。然而，在处理大于3个目标函数以上的优化问题时存在非支配解解集前沿推进速度慢、甚至不收敛，以及解集可视化水平不高等问题[16]。

针对该问题，课题组建立了基于主分量分析(Principal Component Analysis, PCA)的方法进行目标空间相关性分析、降维优化，在不失优化问题主特征的条件下，提取问题的主要特征，实现设计目标的有效降维，详细计算原理，可参考文献[16-17]，图1给出了具体的分析流程，本文研究为提高优化设计效率，在大规模抽样一次分析的基础上，开展PCA相关性分析进行目标空间降维，进一步基于伴随方法进行非冗余目标多目标优化分析。

3 基于“虚拟可行解”与伴随方法的加权函数多目标优化设计

3.1 虚拟可行解方法

毫无疑问，基于离散伴随方法的优化设计尽管在全局性优化问题上存在不足，但在高维设计变量精细化优化问题上具有传统方法不具备的天然优势，完全可以在飞行器气动设计中扮演一种重要的角色。如何高效利用这种优势开展多点优化是一个值得探讨的研究方向。

对于基于梯度信息的多点数值优化设计来说，通常采用的是加权函数处理方式进行高效优化，构造空间目标函数：

F=ω1f1+ω2f2+ω3f3+……

(1)

式中：F为加权目标函数；ωi为各个目标函数的权重；fi为各个目标函数。容易看出，基于这种形式的优化设计结果严重依赖于权函数的选取，在面向具体设计指标开展优化时，权函数的选择存在较大的盲目性。如何合理地、高效地选择权函数是减小设计计算量、提高设计效率、有效满足指标的关键因素，也是设计人员、优化决策系统最为关心的问题，尤其是基于灵敏度的优化设计，该问题显现的更加突出，该项技术是最大程度上挖掘伴随方法优化设计潜力的关键。

图1 基于PCA方法的优化流程[17]Fig.1 Optimization process based on PCA method[17]

为此，本文提出了一种“虚拟可行解”导向性优化方法，其本质是对权函数进行抽样，进行分布式加权优化设计，得到一组设计结果分布，利用神经网络逼近构建虚拟的Pareto前沿，去寻找靠近设计指标要求的权函数组合。具体流程为

1) 对各个设计指标对应的权系数进行抽样分析。与设计变量不同，由于目标函数个数远小于设计变量，因此抽样的个数并不需要太大。

2) 对不同权函数组合在并行环境下，进行独立性优化，由于伴随方法的高效性，此时的计算资源需求并不是很高。

3) 依据各个设计点的优化结果，利用合理数学模型逼近构造虚拟的可行解前沿。

4) 基于“虚拟可行解”前沿预测满足设计指标的权重组合，开展多目标优化，并加入抽样集合。

5) 根据优化结果，判断是否满足设计指标，如果满足停止优化，否则，转向步骤3)。

3.2 基于流场伴随方程求解梯度

飞行器气动优化设计中的最小化问题数学模型可以表达为

minI(W,X)

(2)

式中：目标函数I可以为升阻力、力矩、流量、压比等参数；W、X分别为流场守恒变量、设计变量。显然，在定常流场收敛解的条件下，残差约束R(W,X)=0，进一步引入拉格朗日算子Λ重新构造目标函数：

L=I+ΛTR

(3)

利用链式求导对式(3)进行展开：

(4)

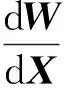
(5)

式(5)就是流场伴随方程，通过隐式迭代方法求解拉格朗日算子Λ之后，可以通过式(6)进行目标函数梯度信息快速求解。

(6)

(7)

可以看出，伴随方程求解完后，流场与伴随变量均保持不变，基于有限差分的导数计算通过扰动设计变量实现，差分步长取1.0×10-4，流场不需要再迭代，此时计算量取决于变形网格计算效率与设计变量个数，由于文中采用了效率极高的并行化RBF-TFI (Radial Basis Functions，TransFinite Interpolation)网格变形技术，64进程并行环境下，处理千万量级网格的时间小于5 s，因此，此时的计算量可以忽略不计。

本文离散伴随方程的结构采用二阶精度的中心格式，人工黏性以及剪切应力输运(SST)两方程湍流模型，采用手工推导方式进行Navier-Stokes方程离散伴随方程构造，并进一步引入虚拟时间项。对式(5)的迭代求解，采用LU-SGS方法隐式时间推进，离散伴随方程各项的物理边界条件采用矩阵形式，冻结湍流黏性系数，由于文中开展全湍流条件下的计算与优化，因此，尽管冻结湍流黏性系数带来一定的误差，但对于优化设计来讲仍然能够较为准确地给出下降方向进行有效设计。黏性项采用薄层近似，离散伴随方程求解时并行机制依然采用与流场并行计算一致的单元数衡量的负载平衡、对等式计算以及MPI消息传递模式。其中，通过MPI进行传递的信息是伴随变量。各个进程中分割面上的两层虚网格上的伴随变量信息以及对接边界条件处理方式，详细处理可以参考文献[18]。

4 宽体飞机标准模型多目标优化与分析

基于宽体飞机CRM标准模型[19]为优化研究算例，进行本文方法的有效性验证。不同的是，为方便进一步开展其他方面的研究，在CRM基础上加入了立尾，且参考点位置与文献[19]不同，但这并不影响本文综合设计方法的有效性验证。优化过程中主要部件同时包含机翼、机身、平尾以及立尾。网格划分为290块，半模网格规模为1 200万量级，如图2所示。流场求解采用自主研发的大规模并行CFD软件PMB3D[20]，伴随变量求解采用自主研发的大规模并行PADJ3D软件[18]，进一步采用并行化RBF-TFI网格变形技术[21]进行梯度信息求解。计算过程采用中心格式，SST湍流模型，LU-SGS时间推进以及多重网格加速收敛技术，64核进行并行计算。关于CFD数值模拟以及伴随梯度数值求解精度校核的具体细节详见文献[16,18]。

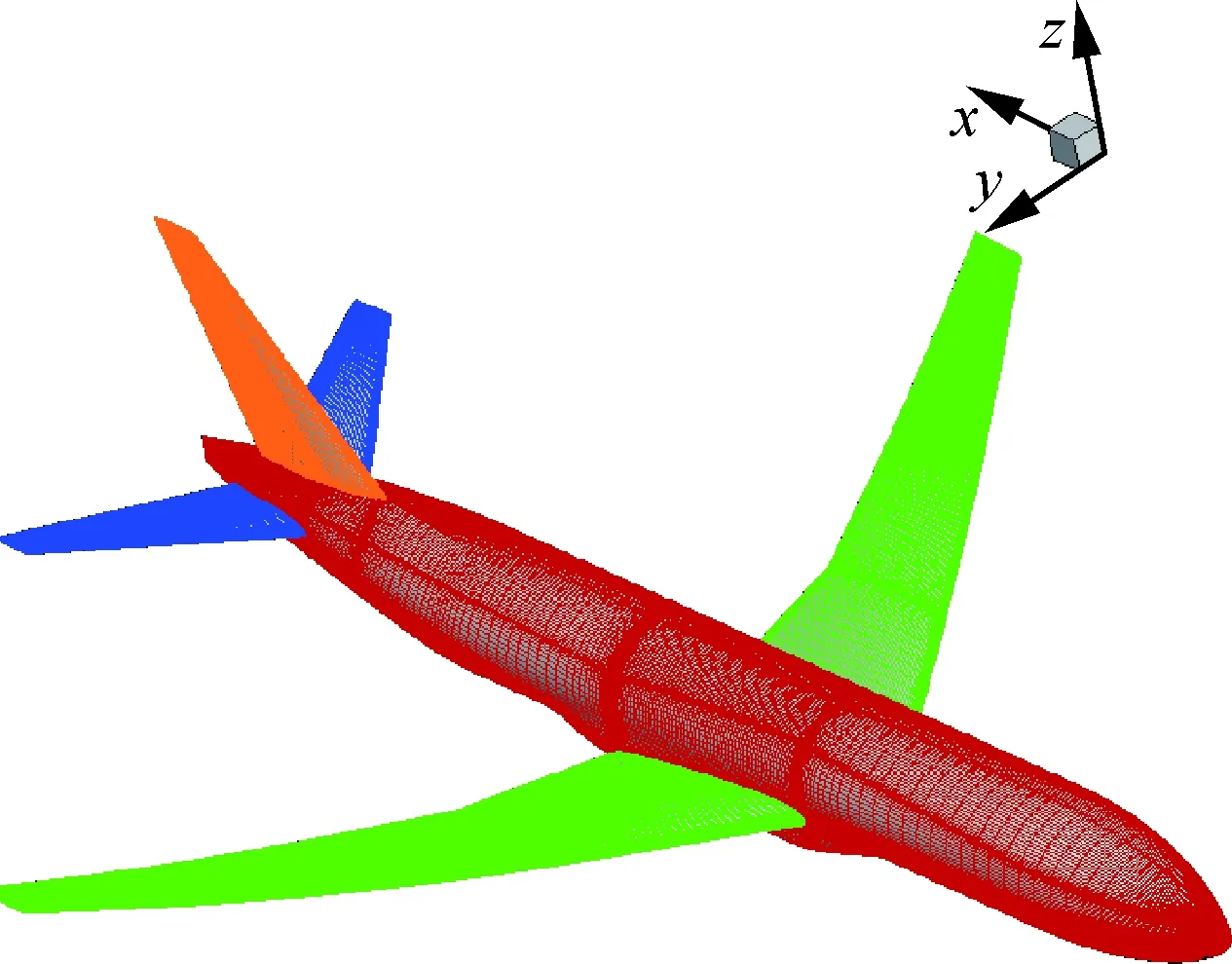
图2 CFD表面网格分布Fig.2 CFD surface gird distribution

超临界机翼采用了基于NURBS基函数的自由式变形(Free Form Deformation，FFD)进行参数化[21]，图3给出了示意图，共采用200个控制顶点实现机翼气动外形参数化建模。该模型的设计要求是在满足几何约束的前提下，对巡航状态升阻比、阻力发散特性、抖振边界以及力矩特性进行综合优化，设计状态为Ma=0.85,Re=5.0×106，其初始优化数学模型为

CL,design=0.5

图3 自由式变形参数化Fig.3 Parameterization of free form deformation

图4 特征值分布Fig.4 Distribution of eigenvalue

图5 相关性分析Fig.5 Correlation analysis

0.87、CL=0.5状态的阻力与Ma=0.85、CL=0.6状态的阻力系数增量的相关性分析示意图，这也是PCA的一个本质作用，即分析目标函数之间的相关性。

依据PCA相关性分析，最终选定f1、f2和f4两个状态为目标函数，其中力矩做约束处理，开展多点优化，并进一步对优化结果进行“冗余目标”验证。

结合伴随优化设计体系，建立加权形式的优化数学模型：

minF=ωf1+(1-ω)f2

式中：ω为权系数。

文中优化过程，为满足升力系数的等式约束条件，采用了定升力系数计算，此时迎角随设计变量变化而变化，是影响灵敏度计算的重要因素，且对灵敏度的计算具有变分贡献，为避免对迎角求解灵敏度，需要消去该项的显式表达[10]。对阻力系数变分：

(8)

进一步考虑升力约束δCL=0变分：

可以得到固定升力系数条件下，迎角变分表达式为

(9)

将式(9)代入式(8)可以得到定升力条件下的阻力系数灵敏度计算表达式：

(10)

基于序列二次规划(SQP)算法，在中国空气动力研究与发展中心1 590万亿次/秒的高性能集群上开展伴随方法加权优化，不同权函数伴随优化采用分布式计算，每个权函数的伴随方法优化采用64核，共采用256核。在为虚拟Pareto 前沿构建提供不同权函数组合数据后，基于虚拟Pareto前沿选择满足0.85～0.87阻力增量不大于20 counts的权函数。

表1给出了设计前后不同外形在不同马赫数的气动特性对比，K表示升阻比，基于“虚拟前沿”导向性权重的多点优化设计在阻力发散特性方面有明显改善，0.85～0.87阻力增量为19.1 counts，巡航升阻比也有明显提高。图6～图7给出了单点优化以及多点优化与初始构型压力系数云图的对比。可以看出，单点优化完全消除表面激波，多点优化呈现弱激波形态。图8给出了不同设计方法的优化历程，红线、绿线分别代表多点设计中Ma=0.85、Ma=0.87状态阻力优化历程曲线，蓝线代表Ma=0.85单点优化历程，各个方法均进行了20代优化。图9给出了展向绝对坐标Y=5、10、15、20 m站位压力分布优化前后对比，相对于初始外形激波强度均大幅减弱，单点设计与多点设计压力分布形态区别主要在kink外翼段。以Y=15 m站位压力分布来分析，单点设计压力分布呈无激波形态，阻力发散、抖振特性较好的多点设计气动外形典型压力分布形态压力恢复位置较初始外形靠前，压力恢复段呈现弱激波形态，紧跟一段较短的加速区(“鼓包状压力分布”)，如图9(c)所示，该加速区再次恢复过程没有出现第2道激波，实际上，该处加速区可以一定程度减缓马赫数增大时激波强度的增加，对阻力发散较为有利。图10给出了不同优化方法设计结果的阻力发散特性对比，图11～图13给出了不同外形的在CL=0.62下的表面极限流线，可以看出，初始外形已经大面积分离，单点优化与多点优化的流动均为小分离泡形式，一定程度上反映了抖振特性的改善，也验证了文中综合分析方法的可行性。

表1 不同设计结果气动特性对比Table 1 Comparison of aerodynamic characteristics between different design results

图6 单点优化设计前后压力云图对比Fig.6 Comparison of pressure contour before and after single-point optimization configuration

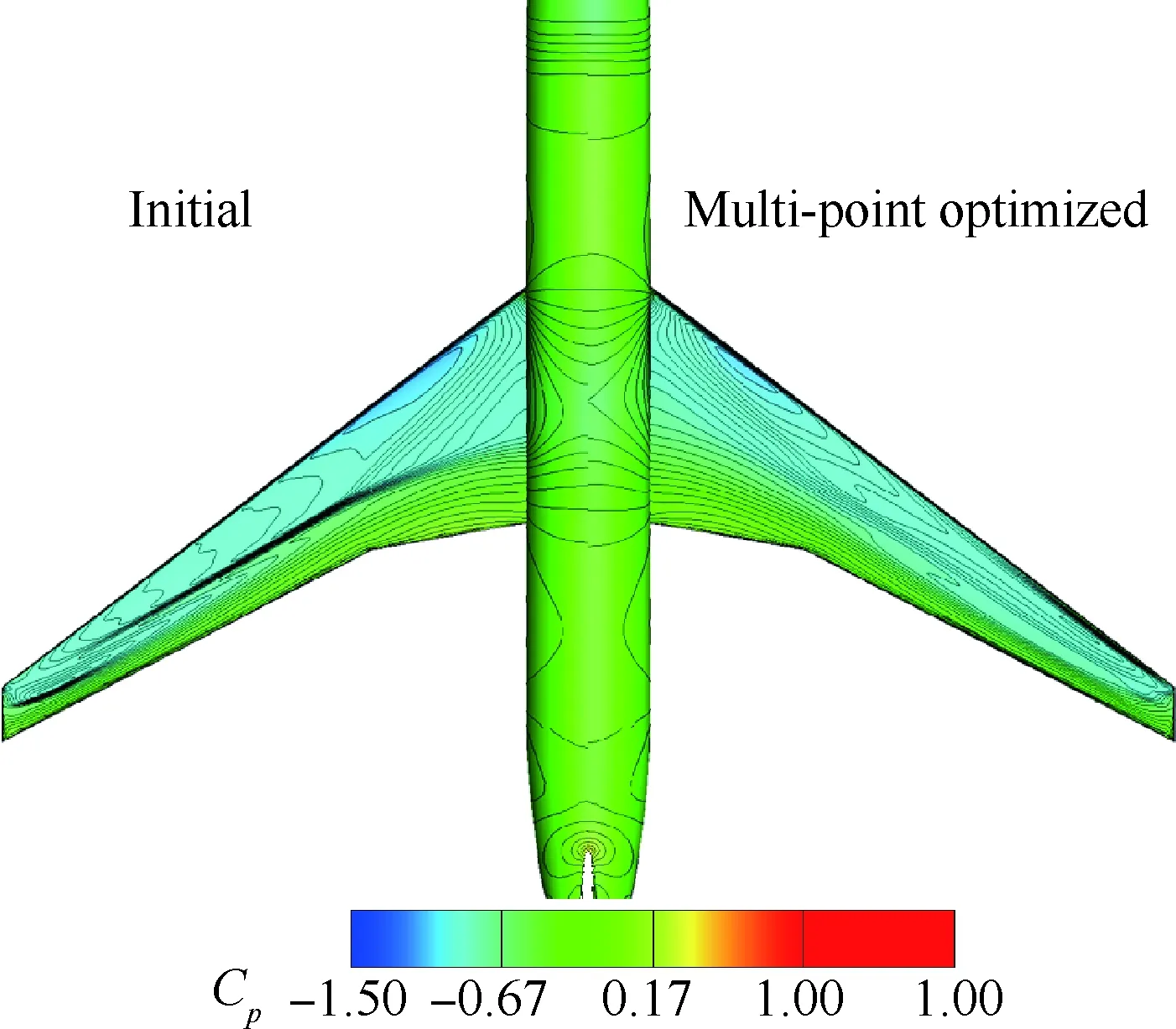
图7 多点优化设计前后压力云图对比Fig.7 Comparison of pressure contour before and after multi-point optimization configuration

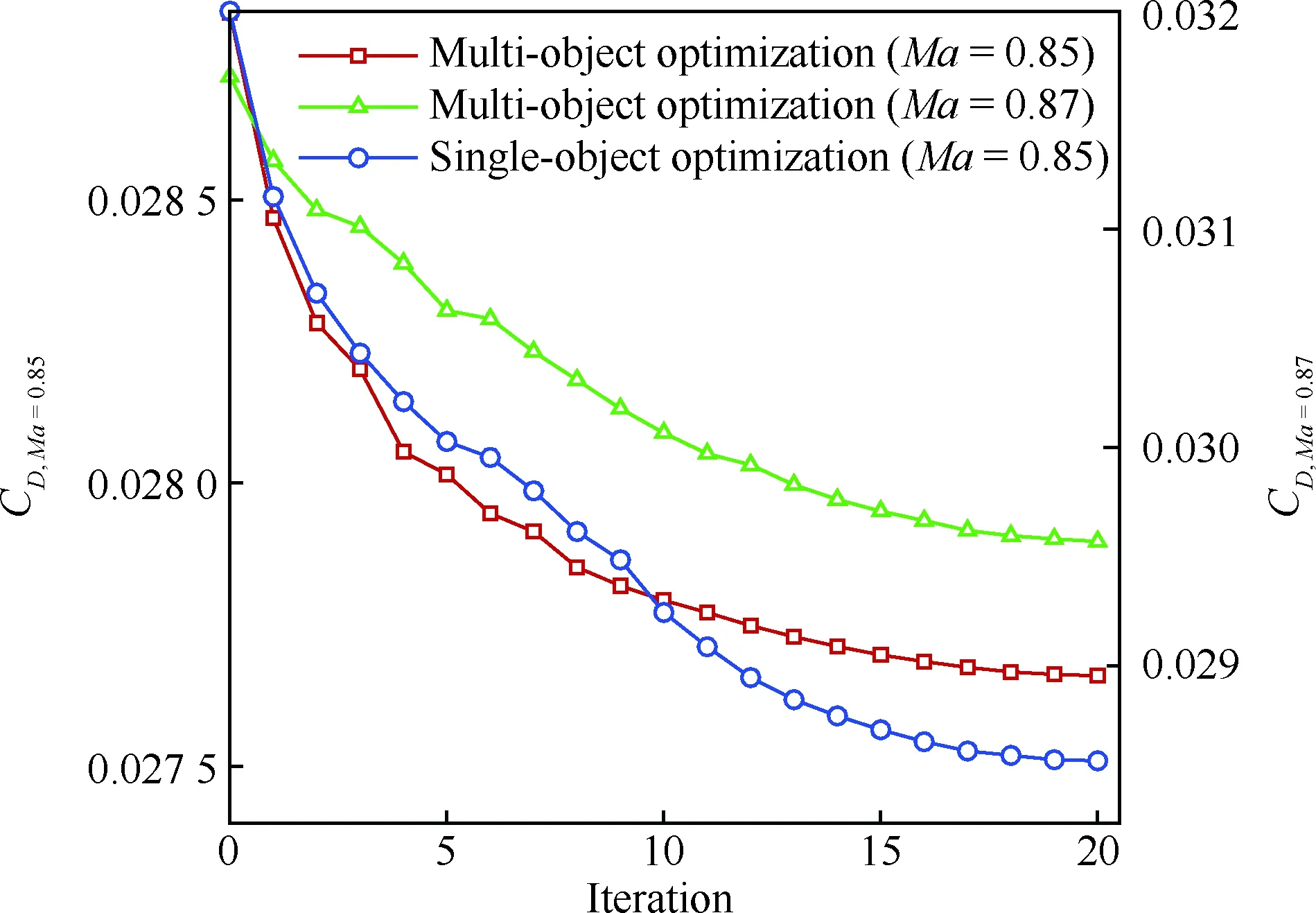
图8 不同方法优化设计历程Fig.8 Optimization design history of different methods

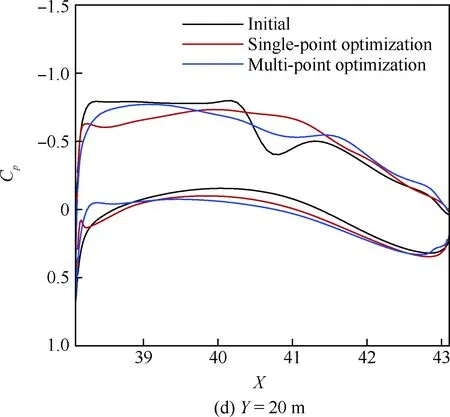
图9 站位优化前后压力分布对比Fig.9 Comparison of pressure distribution before and after station optimization

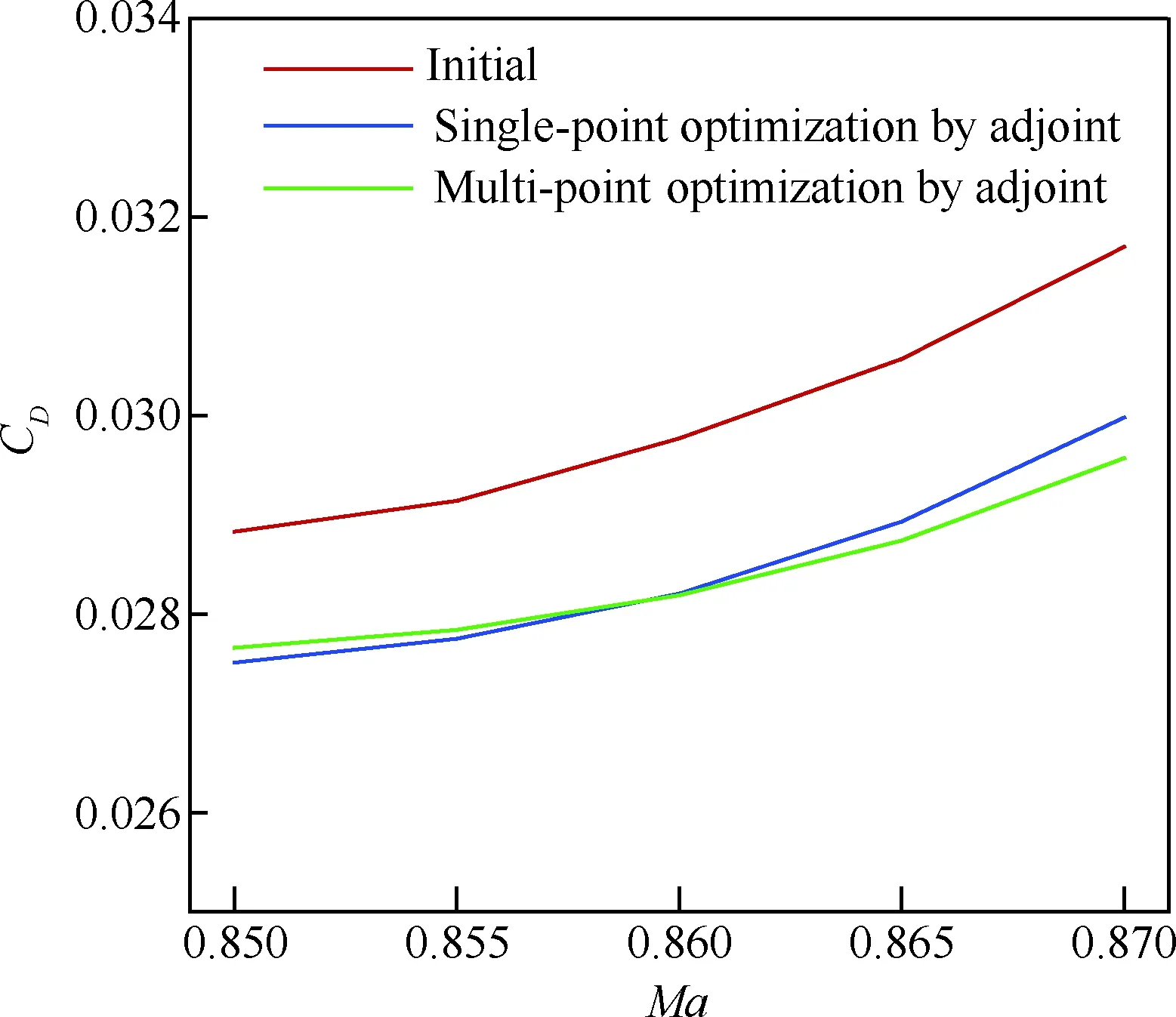
图10 单点与多点设计阻力发散特性对比Fig.10 Comparison of drag divergence between single-point and multi-point designs

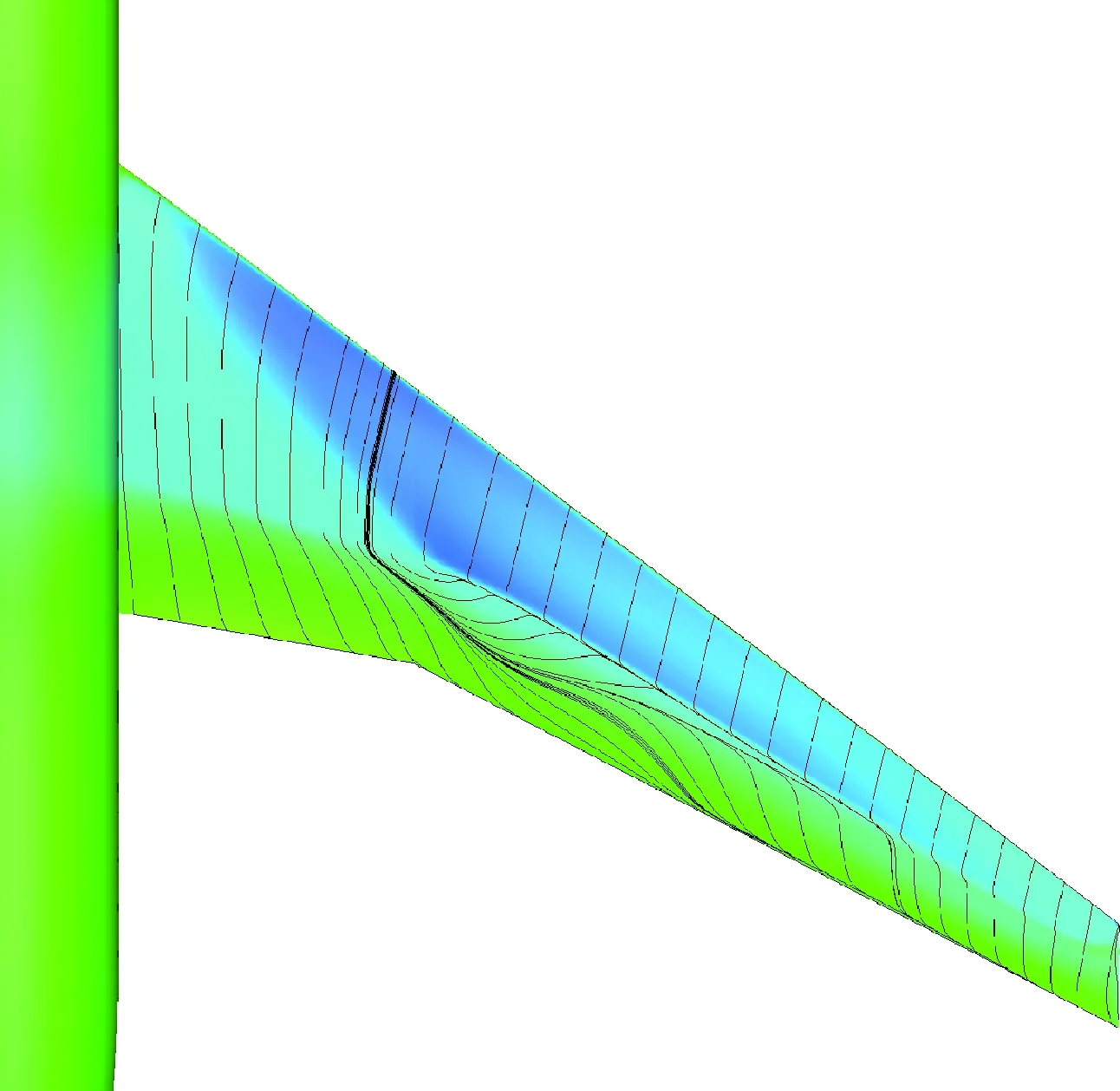
图11 初始外形表面极限流线(CL=0.62)Fig.11 Limit streamlines of initial configuration surface (CL =0.62)

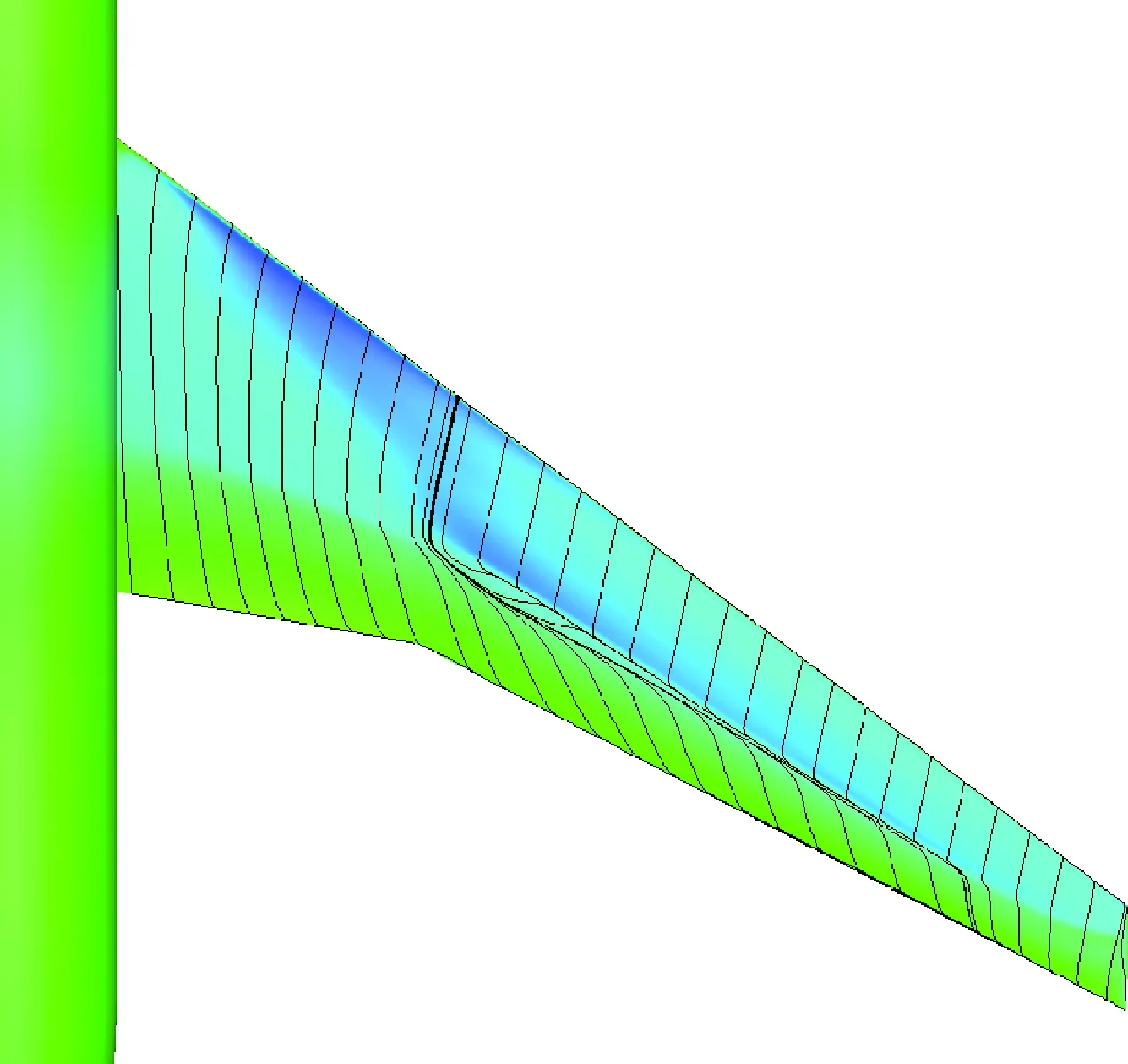
图12 单点优化外形表面极限流线(CL =0.62)Fig.12 Limit streamlines of single-point optimized configuration surface (CL =0.62)

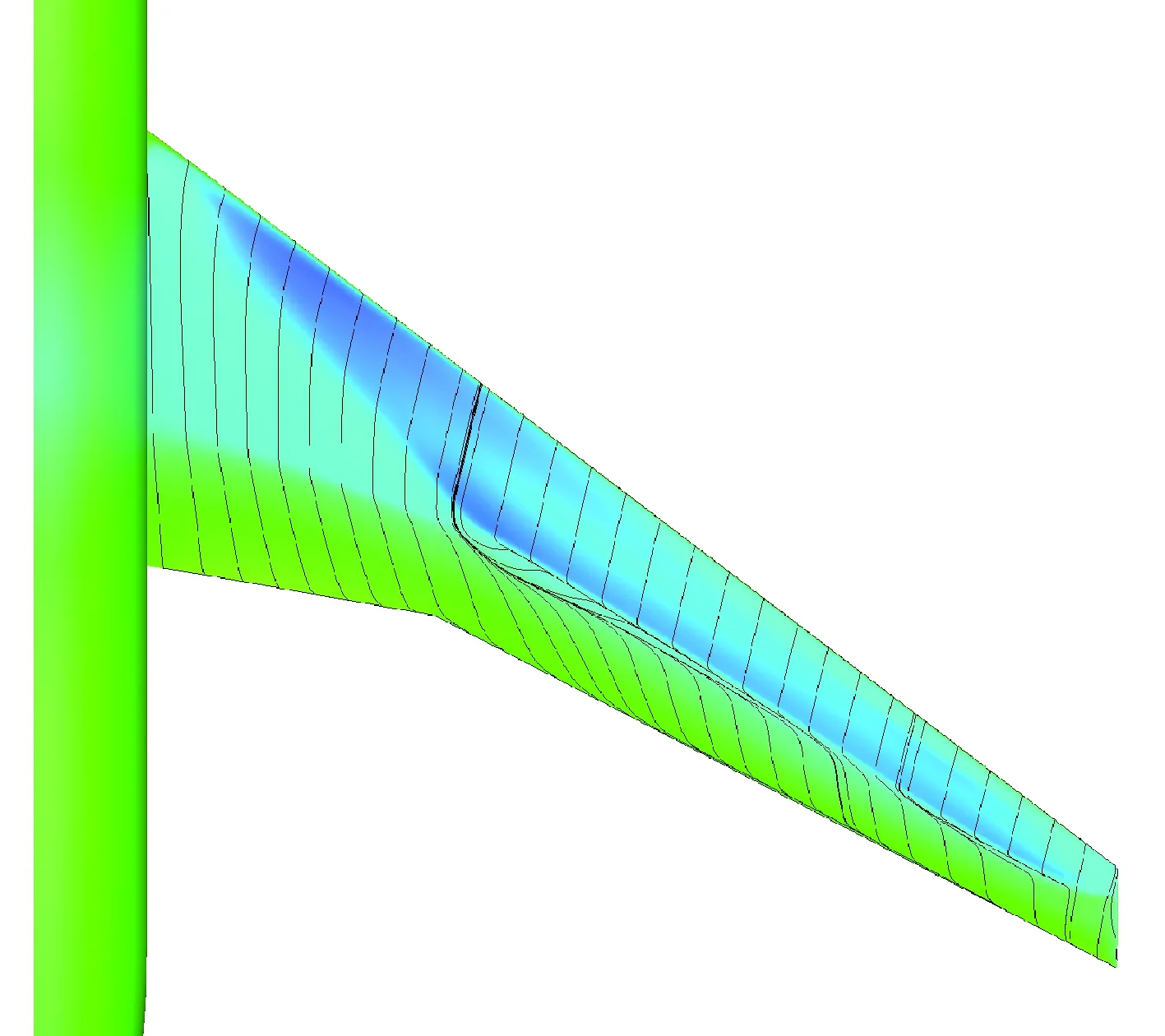
图13 多点优化外形表面极限流线(CL=0.62)Fig.13 Limit streamlines of multi-point optimized configuration surface (CL =0.62)

5 “虚拟可行解”结合伴随方法的进一步分析与讨论

容易理解，对于各个目标函数均为单峰值的问题，加权叠加后，目标函数的峰值特性可能出现两种情况，第一种，加权目标函数依然保持单峰值特性，另外一种，加权目标函数出现多峰值现象，这种依赖于具体问题，图14和图15给出了典型曲面函数叠加结果。

对于加权目标函数依然保持单峰值特性问题，尽管伴随方法具有局部最优特性，仍然可以保持与进化算法优化结果的一致性；对于加权目标函数依然出现多峰值特性问题，优化伴随方法的局部特性，“虚拟可行解”结合伴随方法求解的虚拟Pareto前沿推进效果将劣于进化算法。

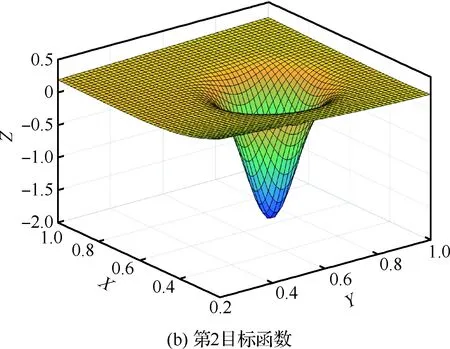
图14 目标函数曲面Fig.14 Surface of object function

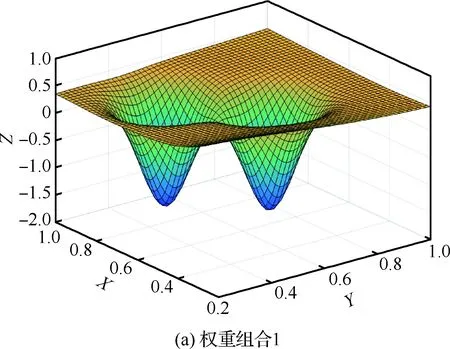
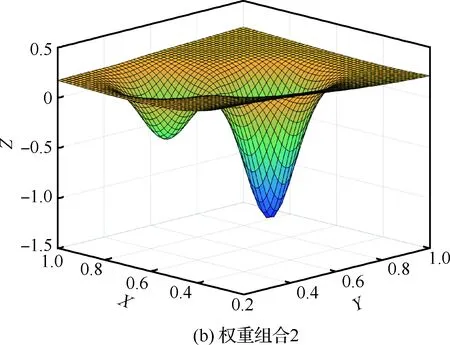
图15 权重组合目标函数曲面Fig.15 Objective function surface of weight combination

该类情况同样可以通过改变初始点的选择从一定程度上消除叠加函数多峰值带来的影响，而如何降低初始点选择的盲目性，是基于伴随理论与“虚拟可行解”方法在具体应用中值得关注的问题，这也是本文进一步的研究内容。在气动设计中，目标函数加权组合均有可能出现单峰值或多峰值情况，且目标函数本身若是多峰值问题，加之高维设计空间因素，加权组合会出现更复杂的现象，设计结果依赖于初始点选择，但对于工程型号设计问题来说，综合分析策略不失为一种简捷高效的优化设计方法，具有较强的工程应用价值。