基于FANP-GCE的“一带一路”PPP基础设施项目风险分担
2019-03-02刘畅旸石振武苗启香
刘畅旸, 石振武, 苗启香
(1. 青岛理工大学 琴岛学院, 山东 青岛 266106; 2. 东北林业大学 土木工程学院, 黑龙江 哈尔滨 150040)
“一带一路”是我国应对全球经济政治发展局势和改革开放重要节点作出的重大战略决策,对推进我国新一轮的对外开放具有重要意义。国家发展的基本要素是基础设施的健全化和网络化。而“一带一路”沿线国家多数为发展中国家,普遍受到资金短缺,建设能力不足等条件的制约,基础设施发展水平落后,从而严重制约了其经济文化的发展。基础设施的建设往往存在资金投入量大,建设周期长和资金回收期长等问题,传统融资模式无法满足基础设施发展的需要。而PPP(Public-Private Partnership)项目融资,即公私合营融资模式,可以通过引入私人资本的方式为政府部门解决这一融资难题。PPP项目融资模式是政府与私营资本针对公共基础设施服务项目,以特许经营权为基础建立的长期合作伙伴关系,其合作目的是利益共享,风险共担[1]。然而,由于“一带一路”沿线存在政治局面复杂,宗教多元化等问题,战争内乱、经济危机等风险系数较高,导致“一带一路”PPP项目在建设经营过程中可能遭遇的风险也随之增大[2]。因此,如何精准地分配PPP项目中公私双方的风险承担比例对于项目的成功至关重要。
为此,国内外专家学者针对PPP项目的风险分担方法进行了广泛深入的研究,然而对于如何量化风险分担系数的研究仍不完善。 王蕾[3]等人结合ANP(Analytic Network Process)理论和合作博弈理论,通过构建PPP项目风险分担模型确定风险分担比例。Jin Xiaohua[4]等人建立PPP项目风险分担人工神经网络模型,通过对模型进行训练和验证,将收集到的数据输入模型得到风险分担系数。王建波[5]等人建立风险分担流程模型,运用线性规划模型计算风险分担系数。总结国内外专家学者的研究结果,目前在PPP项目风险分担领域应用最多的方法是博弈论[6],但由于其无法考虑风险影响因素间的相互影响,因此存在一定缺陷。另外,各类方法普遍针对的是国内PPP项目,对于国际合作模式,尤其是对于环境更为复杂的“一带一路”PPP项目风险分担的研究较少。本文拟针对“一带一路”项目中存在的共担风险,构建FANP(Fuzzy Analytic Network Process)网络模型,综合考虑风险影响因素间的相互影响作用,得出各影响因素的权重。继而结合灰色聚类评价理论,构建白化权函数,得出共担风险在公私双方间的分担比例。
1 风险分担框架
1.1 风险分担原则
“一带一路”PPP基础设施建设项目的风险分担应遵循以下三个原则[7]:(1)由最具备承受能力的一方承担该风险,若双方均不具备完全承担风险的能力,则需要由双方共同承担该风险;(2)风险收益对等原则,即越高的风险承担比例对应越高的收益回报;(3)承担的风险有上限。而若不遵循以上原则,不必要的高额风险溢价可能会导致项目失败。
1.2 风险分担流程
风险分担主要分为三个阶段,分别为风险识别,风险分配和计算风险分担系数。
第一阶段为风险识别。本文通过阅读相关文献[8~10],并结合专家意见,对PPP项目风险因素进行归纳,将“一带一路”PPP项目面临的风险分为7种一级风险,以及由其衍生的25种二级风险,详见表1。
第二阶段为风险分配。本阶段是在风险识别的基础上,判断风险应由政府或私营部门单独掌控,还是由公私双方共同承担。本文通过总结相关文献[9],得出风险分担一般结论,详见表1。

表1 “一带一路”PPP基础设施项目风险分担结果
第三阶段为计算风险分担系数。该阶段主要针对需要公私双方共同承担的风险,构建FANP-GCE(Gray Comprehensive Evaluation)数学模型,计算风险分担系数。
2 FANP-GCE方法概述
建立风险分担模型的关键是信息的采集和量化。为解决该核心问题,首先需明确评价信息的特点。由于PPP项目所面临的风险具有部分信息未知的特性和复杂性,即风险分担系统是一个灰色系统,介于信息完全明确的白色系统和信息完全未知的黑色系统之间。而灰色聚类分析理论可通过白化权函数和灰色聚类权矩阵实现对“小样本、贫数据、不确定”信息的白化,从而实现对风险分担的量化[11]。
同时,在风险分担过程中必定会涉及风险影响因素的赋权。“一带一路”PPP项目风险分担是一个受多因素影响,且各因素之间也存在相互影响的复杂决策问题,具有明显的模糊性。因此本文在引入网络分析法(ANP)的基础上,结合三角模糊判别理论对专家的决策信息进行处理,最终构建FANP赋权模型。该模型可对认知不清、难以量化的风险影响因素进行量化和赋权,削弱了专家在打分过程中的主观影响,使最终结果更加精准。
2.1 构建ANP风险分担模型
网络分析(ANP)模型包含控制层、网络层和方案层[12]。控制层包含问题目标G和控制准则B。本文中的问题目标为“一带一路”PPP基础设施项目风险最优分担比例,控制准则为公私双方共同承担风险Rij的有效控制。
第二层为网络层。依据风险分担原则,结合“一带一路”PPP基础设施项目运作方式,总结出风险分担的四大影响因素,分别为风险承担意愿、风险应对能力、风险自有属性和项目属性。各主要影响因素下分别包含若干二级影响因素。影响因素间均存在相互作用关系。风险分担影响因素体系详见表2。

表2 “一带一路”PPP基础设施项目风险分担影响因素体系
第三层为方案层,即“一带一路”PPP基础设施项目公私双方对风险的最优分担比例,表示为P=[P1,P2],其中P1为政府部门风险分担系数,P2为私营部门风险分担系数,且P1+P2=1。“一带一路”PPP基础设施项目风险分担ANP模型详见图1。

图1 “一带一路”PPP基础设施项目风险分担ANP模型
2.2 构建三角模糊判别矩阵
以控制标准B“共担风险Rij的有效控制”为准则,邀请n位专家针对风险Rij对同一层次的影响因素指标的重要程度进行两两比较。为降低专家打分法的模糊性和不确定性,引入三角模糊数取代传统1~9标度法,通过专家对指标重要程度的评判,得到三角模糊判别矩阵[13]。
设M=(l,m,u)为一三角模糊数,其隶属度函数μM(x)为:
(1)
式中:l≤m≤u,且u,l分别为三角模糊数M的上限和下限,m为M的最大可能值。
根据表3所示的模糊语言得到三角模糊判别矩阵U,如式(2)所示。式中mij表示第i行第j列的三角模糊数。

表3 模糊语言与其对应的三角模糊数
(2)


(3)
M1≥M2的可能度为:
V(M1≥M2)=hgt(M1∩M2)=μM1(d)=
(4)
式中:d为三角模糊数M1,M2交界处的值。
为比较三角模糊数M1和M2的大小,需求得V(M2≥M1)和V(M1≥M2)两者的值。由此得知,一个三角模糊数M的值大于k个三角模糊数Mi(i=1,2,...,k)的可能度为:
V(M≥M1,M2,…,Mk)
=V[(M≥M1),(M≥M2),…,(M≥Mk)]
=minV(M≥Mi),i=1,2,…,k
(5)
设d′(Ai)=minV(Si≥Sk),k=1,2,…,n;k≠i,其中Ai为第i个一级评价指标,可求得评价指标的权向量为:
W′=(d′(A1),d′(A2),…,d′(An))T
(6)
对权向量进行归一化处理,即:
(7)
最终,评价指标的非模糊权向量为
W=(d(A1),d(A2),…,d(An))T
(8)
2.3 风险分担的灰色聚类评价
因项目风险分担影响因素诸多且意义不同,所以当聚类指标的量纲不同且在数量上差异悬殊时,可对各聚类指标事先赋权,这种方法称为灰色定权聚类评估[12]。
2.3.1构建白化权函数
设风险分担系数取值范围为[0,1],将政府部门针对风险Rx的风险分担比例定为五个灰类,对应的风险分担比例为“极少量承担,少量承担,等量承担,大量承担,极大量承担”。每个灰类取值范围如下表所示。

表4 “一带一路”PPP项目风险分担比例划分标准
由此可确定各灰类中心点向量为X=(0.9,0.7,0.5,0.3,0.1)。实践中也可针对不同精度需求增加或减少灰类数量。
根据评价指标风险分担内涵对各灰类建立其对应的白化权函数。设有n个灰类e1,e2,…,en,其对应的白化权函数为f1(x),f2(x),…,fn(x)。本文共有5个灰类,根据风险分担规定的赋值内涵,可确定各灰类的白化权函数,如表5所示。
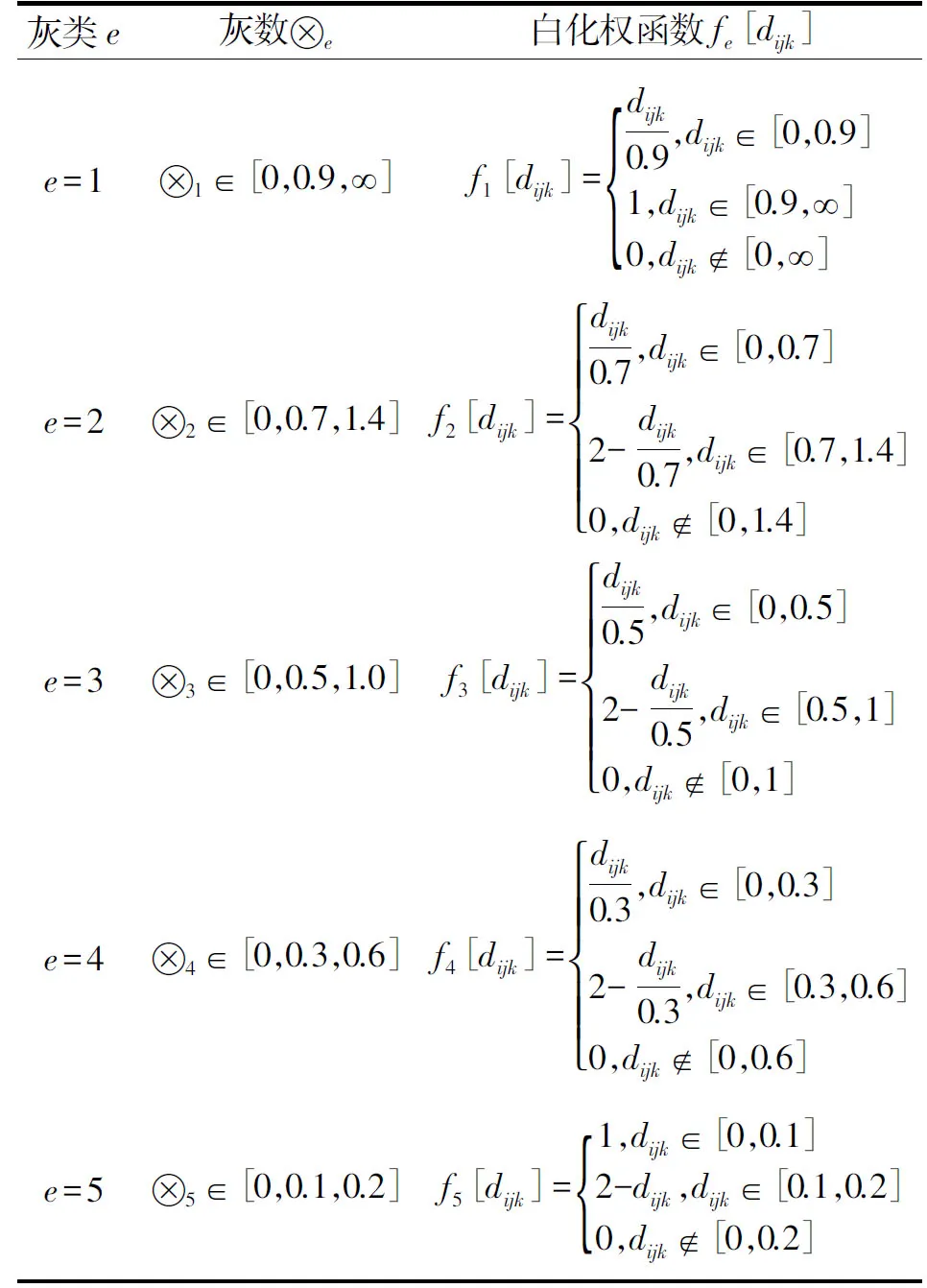
表5 各灰类及对应的白化权函数
注:dijk为第k个专家对第i个指标下第j个二级指标的赋值
2.3.2构建灰色聚类权矩阵
基于灰色系统的内涵,专家对评价指标的赋值均为灰数,邀请n个专家针对共担风险Rx对Cij单独影响下的政府部门分担比例进行赋值,得到n个灰数dij1,dij2,…,dijn。因此,专家组对指标Cij归属于第e个灰类的白化权函数为
(9)
总评价系数为
(10)
由此可求得灰色聚类权向量
(11)
式中:rije表示指标Cij属于e灰类的强度,rije越大表明Cij越应属于e灰类。指标Cij属于各个灰类的灰色评价权向量可表示为rij=(rij1,rij2,rij3,rij4,rij5)。汇总rij,得到政府部门对风险Rx在一级指标Ci单独影响下的灰色聚类权矩阵GRi。
(12)
综合灰色聚类权矩阵GRi,非模糊权向量Wi和中心点向量X,得到政府部门针对风险Rij在一级影响因素Ci单独作用下的风险分担系数。
zi=GRi·Wi·XT
(13)
从而汇总得风险分担系数矩阵Z。
Z=(Z1,Z2,Z3,Z4,Z5)
(14)
结合5个一级影响因素Ci相对于控制指标B的权重W,可求得政府部门针对共担风险Rx的风险分担比例P。
P=W*·Z
(15)
式中:W*为一级影响因素指标权重。
3 实证分析
哥伦比亚马道斯(Mar2)高速公路项目,为“一带一路”在美洲地区的第一个PPP基础设施项目。该项目通过公开招标的方式与中国港湾工程有限责任公司牵头的联合体达成合作协议,并且于2015年10月成立项目公司,该项目预计总投资6.56亿美元,运作方式为BOT(Build-Operate-Transfer)。中方企业的特许经营期为23年。该项目目前处于建设期,预计2019年正式完工通车。
3.1 基于FANP确定风险因素权重
本案例以公私双方共同承担风险R71定价机制为例进行风险分担。依据三角模糊数评判标准,邀请专家组对风险R71下辖的一级及二级风险因素在同级之间进行两两比较,构建三角模糊判别矩阵。以一级影响因素指标C1风险承担意愿为例,得到其所属二级指标的三角模糊判别矩阵,如表6所示。
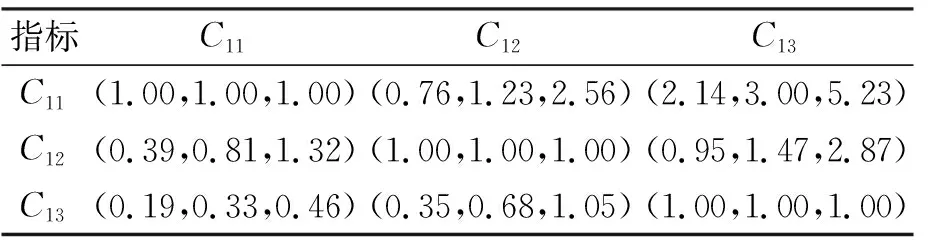
表6 指标C1下辖二级指标三角模糊判别矩阵
根据上文,将三角模糊数判别矩阵进行求解。
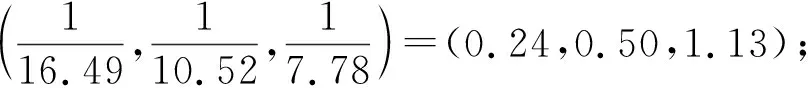
根据公式(4)得到
V(S1≥S2)=1,V(S1≥S3)=1,
V(S2≥S3)=1,
根据公式(5),得到
d′(C1)=V(S1≥S2,S3)=min(1,1)=1,
d′(C2)=V(S2≥S1,S3)=min(0.69,1)=0.69,
d′(C3)=V(S3≥S1,S2)=min(0.21,0.6)=0.21。
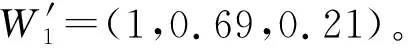
同理可得其他所有二级指标以及一级指标权重如下:
W2=(0.47,0.25,0.28),W3=(0.14,0.29,0.31,0.26),W4=(0.21,0.35,0.21,0.23),W*=(0.32,0.28,0.19,0.21)。
3.2 灰色聚类评价
根据三角模糊评价语言集,邀请10名专家围绕该项目的定价机制风险在二级影响因素Cij单独影响下的政府部门风险承担比例进行灰数赋值,由此构造风险分担决策矩阵如下:
D1=

D2=

D3=

D4=

根据上文所述构建灰色聚类权矩阵如下:
根据公式(13),可求得政府部门针对风险GR71在一级影响指标C1单独作用下的风险分担系数z1。
z1=GR1·W1·XT=0.682
同理可求得政府部门针对风险R71在其余三个一级指标Ci单独影响下的风险分担系数z2,z3,z4分别为:z2=0.721,z3=0.647,z4=0.731。
汇总得风险分担系数矩阵Z,Z=[0.6820.7210.6470.731]。
结合公式(15),得政府部门对共担风险R71的风险分担比例P,P=Z·W*=0.697。
同理,求得私营部门对共担风险R71的风险分担为0.303。
4 结 论
(1)本文将“一带一路”PPP基础设施项目的风险分担作为一个灰色且模糊的系统,结合模糊网络分析(FANP)和灰色聚类评价方法(GCE),综合考虑了风险分担影响因素间的相互作用,构建了FANP-GCE数学模型;
(2) FANP赋权模型是以传统的AHP和ANP方法为基础提出的改进方法,使之与模糊集理论相结合,从而实现了对认知不明确的信息进行合理量化,极大地削弱了专家打分时的主观影响,提高了对影响因素赋权的准确度;
(3)本文运用FANP-GCE模型,实现了“一带一路”PPP项目在公私双方间的合理风险分担,并通过案例证明了该模型的实际运用价值。
