聚焦2018年高考中圆锥曲线的离心率问题

■江苏省无锡市第六高级中学 张 钢

■江苏省无锡市青山高级中学 张启兆

圆锥曲线的离心率是近年高考的一个热点,有关离心率的试题综合性较强,灵活多变,能有效地考查考生的数学核心素养。这类问题的解法有讲究,如果我们能掌握规律,抓住关键,就能轻松解决圆锥曲线的离心率的有关问题。那么,关键是什么呢?规律有哪些呢?下面以2 0 1 8年高考中的圆锥曲线的离心率问题为例,介绍圆锥曲线的离心率问题的解法(主要是抓住“一二三四五”),希望对同学们有所帮助。

一个关键:建立a、b、c(a、b、c中的2个或3个)的关系;

两个入口:从“形”入手,从“数”入手;

三个方向:从定义的角度出发,从方程的角度出发,从几何特征的角度出发;

四种工具:平面几何基础知识,平面向量,三角函数,参数方程;

五种思想:数形结合思想,方程思想,函数思想,转化思想,分类讨论思想。

一、求离心率的值

根据题目给定的条件,合理建立含有a、b、c的等式即可求出e的值。

例1 (2 0 1 8年高考全国卷Ⅱ文第1 1题)已知F1,F2是椭圆C的两个焦点,P是C上的一点,若P F1⊥P F2,且∠P F2F1=6 0°,则C的离心率为( )。

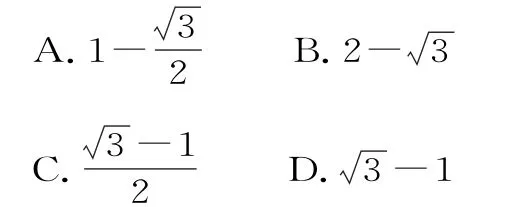
解:(以“形”入手,利用“定义”)

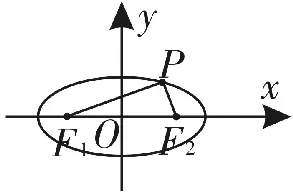
图1

例2 (2 0 1 8年高考全国卷Ⅱ理第1 2题)已知F1,F2是椭圆C:的左、右焦点,A是C的左顶点,点P在过A且斜率的直线上,△P F1F2为等腰三角形,∠F1F2P=1 2 0°,则C的离心率为( )。

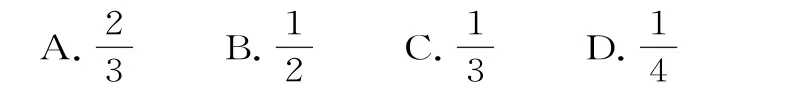
解:(以“形”入手,利用图形中隐含的条件建立方程)

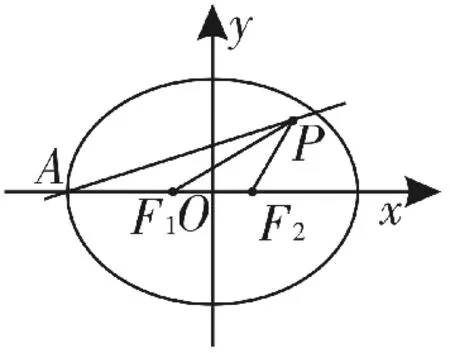
图2

如图2所示,由题意知A(-a,0),F1(-c,0),F2(c,0),∠F1F2P=1 2 0°,所以直线A P:y(x+a),直线立两直线方程解得。由△P F1F2是顶角为1 2 0°的等腰三角形,得直线F1P的倾斜角是3 0°,则即,化简得a=4c,则椭圆的离心率为故选D。

评注:注意圆锥曲线的离心率的问题中,常给出一些特殊多边形,其中多含有圆锥曲线的某些特殊点或线段。从定义出发,观察图形特征,寻求其中的联系,找到a、c关系或建立有关a、b、c的齐次方程f(a,b,c)=0是求解的关键。

例3 (2 0 1 8年高考全国卷Ⅲ理第1 1题)设F1,F2是双曲线b＞0)的左、右焦点,O是坐标原点。过F2作C的一条渐近线的垂线,垂足为P。若|P F1|=C的离心率为( )。

解法1:(以“数”入手,结合“方程”)

图3

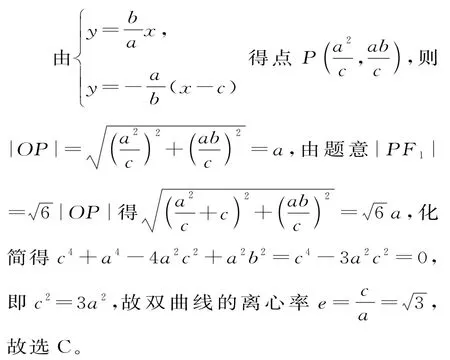
评注:求圆锥曲线的离心率也可从代数角度入手,利用直线方程求交点、点线距离、斜率等方法,以向量和参数作为工具,找到曲线上点的坐标,再将其代入曲线方程,转化为a、c的等量关系。

此外,本题还可以利用特殊化、余弦定理等方法求解,不一一列举。

解法2:(以“形”入手,结合已知条件,利用勾股定理建立等量关系)

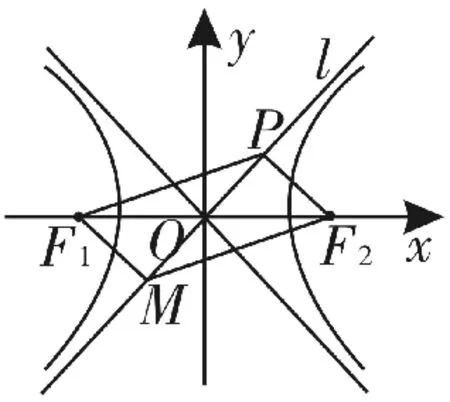
图4

在R t△P O F2中,O P

过F1作F1M⊥l于M,由对称性知,四边形P F1MF2为平行四边形,所以|MF2|=

在R t△MP F2中,PM2+P F22=MF22即4a2+b2=6a2,即2a2=b2。

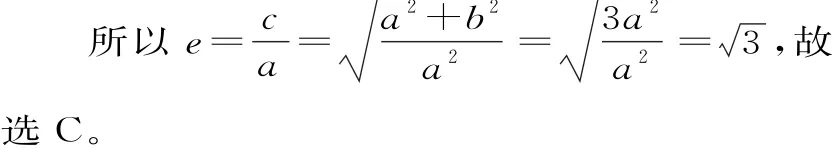
评注:以“形”入手,利用圆锥曲线的性质,把已知条件中的等量关系“翻译”成a、b c间的等量关系,也是求圆锥曲线的离心率值的通法之一。本题考查双曲线的性质及其应用,解题时要注意挖掘隐含条件,如双曲线(a＞0,b＞0)的焦点(c,0)到渐近线的距离为b,要注意积累这些解题经验。

二、已知离心率的值求圆锥曲线方程

例4 (2 0 1 8年高考天津卷理第7题已知双曲线(a＞0,b＞0)的离心率为2,过右焦点且垂直于x轴的直线与双曲线交于A,B两点。设A,B到双曲线同一条渐近线的距离分别为d1和d2,且d1+d2=6,则双曲线的方程为( )。

解:(以“形”入手,结合已知条件,利用勾股定理建立等量关系)

图5

评注:已知圆锥曲线的离心率,解题时就可以把a、b、c三个量统一成一个量,从而简化计算。

三、求离心率的范围(或最值)

求解此类题,关键是找到含有a、b、c的不等式,进而找到解决问题的突破口。

例5 (2 0 1 8年高考全国卷Ⅰ理第1 1题改编)设双曲线的左、右焦点分别为F1,F2,点P在双曲线的右支上,且P F1=4P F2,则此双曲线离心率的最大值为____。

解:(从几何特征的角度出发寻找不等关系)如图6,设P F2=m(m＞0),由P F1=4P F2得P F1=4m,由双曲线的定义得P F1-P F2=2a。

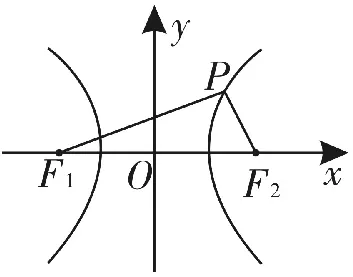
图6

由平面几何知识得P F1+P F2≥F1F2(当且仅当点P为双曲线的右支与x轴的交点时取等号),所以5m≥2c,即所以此双曲线离心率的

评注:求圆锥曲线的离心率的取值范围或最值等问题,利用圆锥曲线的定义及平面几何知识,建立a、c之间的不等关系是一种通法。本题以“三角形中任意两边之和大于第三边”为依据,建立了a、c之间的不等关系。

例6 (2 0 1 8年高考北京卷理第1 4题改编)设双曲线C的中心为点O,若有且只有一对相交于点O,所成的角为6 0°的直线A1B1和A2B2,使|A1B1|=|A2B2|,其中A1,B1和A2,B2分别是这对直线与双曲线C的交点,则该双曲线的离心率的取值范围是___。

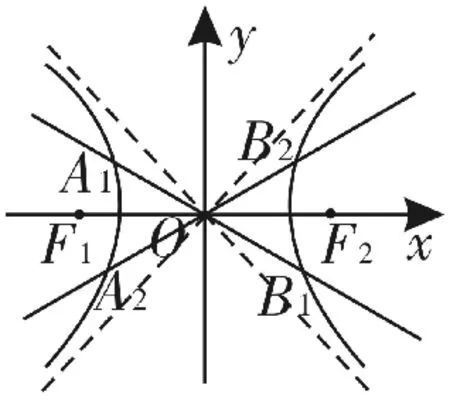
图7

解:设双曲线的焦点在x轴上,如图7。由双曲线的基本性质可知,直线A1B1和A2B2关于x轴对称。分类讨论:

(1)若直线A1B1和A2B2与x轴的夹角均为

3 0°,则双曲线的渐近线与x轴的夹角大于3 0°,且小于或等于6 0°,否则将会有二对相交于点O、所成的角为6 0°的直线A1B1和A2B2,不满足题意。由作图知双曲线的一条渐近线的斜率

(2)若直线A1B1和A2B2与x轴的夹角均为6 0°,则将会有二对相交于点O、所成的角为6 0°的直线A1B1和A2B2,不满足题意。

评注:以“形”入手,寻找不等关系,也是求圆锥曲线的离心率的取值范围或最值的通法之一。本题考查双曲线的性质及其应用,解题时要注意挖掘隐含条件。本题的易错点是误认为就满足条件了,从而错求为