椭圆新颖问题追踪

■甘肃省陇南市礼县职业中等专业学校 杨 虎 撒 波

一、椭圆中的定点问题

例1 (2 0 1 8届高三“荆、荆、襄、宜四地七校考试联盟”1 0月联考数学)已知椭圆E的中心在坐标原点,焦点在坐标轴上,且经过

(1)求椭圆E的方程。

(2)在直线x=4上任取一点T(4,m)(m≠0),连接T A,T B,分别与椭圆交于M、N两点,判断直线MN是否过定点。若过,求出该定点;若不过,请说明理由。

解析:(1)设椭圆方程为m x2+n y2=1(m＞0,n＞0)。将A(-2,0),B(2,0),代入椭圆方程,得

综上,直线MN恒过定点(1,0)。

点评:本题考查椭圆的标准方程以及直线与圆锥曲线的位置关系。第一问可以设出椭圆的方程为m x2+n y2=1,将点的坐标代入可求得m,n的值,即可得椭圆的方程;第二问联立方程组,根据根与系数的关系可以求得M、N的坐标,进一步证明直线MN恒过定点(1,0)。追踪:(2 0 1 6年湖南高中数学竞赛试题已知椭圆经过点经过椭圆C的右焦点F交椭圆于A,B两点,点A,F,B在直线x=4上的射影依次是D,K,E。

(1)求椭圆C的方程。

(2)连接A E,B D,试探求当直线l的倾斜角变化时,直线A E与B D是否相交于定点。若是,请求出定点的坐标,并给予证明若不是,请说明理由。

解析:(1)点在椭圆上,则b=3由离心率为得a=2。椭圆C的方程为

(2)当直线l的斜率不存在时,直线l⊥x轴,则A B E D为矩形,由对称性知直线A E与B D相交于F K的中点,由此猜想直线A E与B D相交于定点

设A(x1,y1),B(x2,y2),D(4,y1)E(4,y2),直线A B的方程为y=k(x-1)联立椭圆C的方程消去y得:

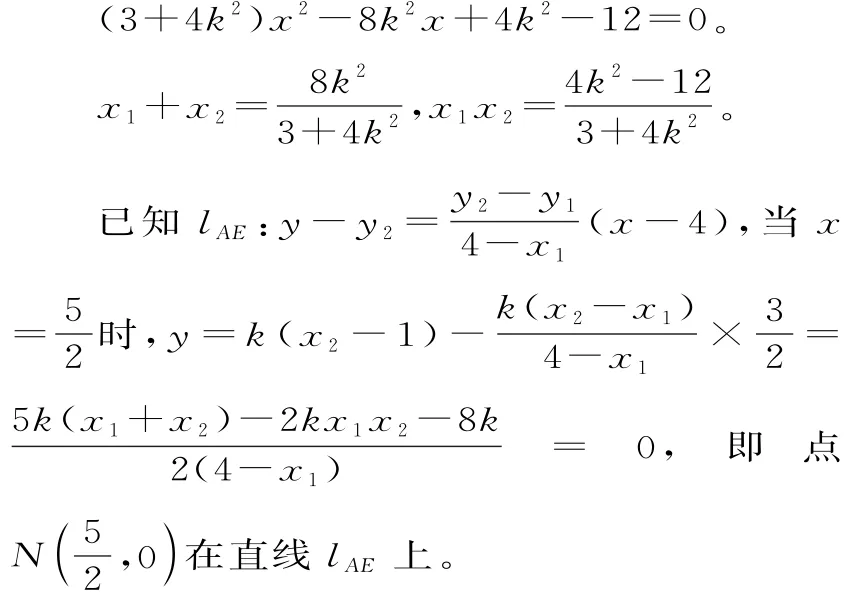
点评:直线方程与椭圆方程联立是求解本题的突破口,由对称性知直线A E与B D相交于F K的中点在证明时只需说明点在直线lAE上。又点N在直线lBD上,故两直线相交于定点。

二、椭圆中的斜率问题

例2 已知椭圆的离心率是椭圆的两个焦点,P是椭圆上任意一点,且△P F1F2的周长是6。

(1)求椭圆C的方程;

解析:(1),可知a=2c。因为△P F1F2的周长是6,所以2a+2c=6。解得a=2,c=1,所求椭圆方程

(2)椭圆的上顶点为M（0,3）,设过点M与圆T相切的直线方程为y=k x+3。

点评:本题中第一问椭圆的离心率已知,间接给出了a与c的关系,结合三角形的周长可解得b,则椭圆方程可求。第二问中主要利用了斜率公式以及函数的单调性来求解斜率的范围。

追踪:(广东惠州市2 0 1 9届高三第一次调研考试理科数学)如图1,椭圆b＞0)经过点A(0,-1),且离心率为

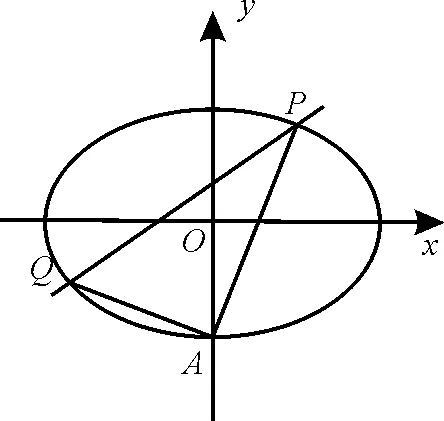
图1

(1)求椭圆E的方程。

(2)经过点(1,1),且斜率为k的直线与椭圆E交于不同两点P,Q(均异于点A),证明:直线A P与A Q的斜率之和为定值。

解析:(1)由题意知1,a=2,椭圆E的方程为

(1+2k2)x2-4k(k-1)x+2k(k-2)=0。由题意知Δ＞0。设P(x1,y1),Q(x2,y2),且x1x2≠0,则所以2,故直线A P与A Q的斜率之和为定值。

点评:本题主要考查了直线的方程及直线与椭圆的位置关系,是高考考查的热点问题,求椭圆方程的方法就是由条件建立方程,利用好根与系数的关系求解。

三、椭圆中的范围问题

例3已知P为椭圆个动点,过点P作圆(x+1)2+y2=1的两条切线,切点分别是A,B,则的取值范围为( )。

图2

点评:通过解直角三角形求出P A,P B的长,再利用向量的数量积与三角函数的化简变形,最后利用基本不等式求解,一气呵成。

追踪:已知F1,F2分别为椭圆的上、下焦点,F1是抛物线C2:x2=4y的焦点,点M是椭圆C1与抛物线C2在第二象限的交点,且

(1)求椭圆C1的方程;

(2)与圆x2+(y+1)2=1相切的直线l:y=k(x+t)(其中k t≠0)交椭圆C1于点A,B,若椭圆C1上一点P满足求实数λ2的取值范围。

四、椭圆中的参数问题

例4的右顶点为A,上顶点为B。已知椭圆的离心率为。

(1)求椭圆的方程。

(2)设直线l:y=k x(k＜0)与椭圆交于P,Q两点,l与直线A B交于点M,且点P,M均在第四象限。若△B PM 的面积是△B P Q面积的2倍,求k的值。

解析:(1)设椭圆的焦距为2c,由已知得又由a2=b2+c2,可得2a=3b。

(2)设点P的坐标为(x1,y1),点M的坐标为(x2,y2),由题意知x2＞x1＞0,点Q的坐标为(-x1,-y1)。由△B PM的面积是△B P Q面积的2倍,可得|PM|=2|P Q|,从而x2-x1=2[x1-(-x1)],即x2=5x1。易知直线A B的方程为2x+3y=6,由方程组消去y,可得。由方程组消去,解得x=y1。由x2=5x1,可得 9k2+4=5(3k+2),两边平方,整理得1 8k2+2 5k+8

点评:本题主要考查椭圆的标准方程和几何性质、直线方程等基础知识,重点关注同学们用代数方法研究圆锥曲线的性质,运算求解能力以及用方程思想解决问题的能力。追踪:(2 0 1 8届北京丰台二模理科数学试题)已知椭圆=1(a＞b＞0)的长轴长为4,离心率,过右焦点F且不与坐标轴垂直的直线l与椭圆相交于M,N两点,设点P(m,0),记直线PM,PN的斜率分别为k1,k2。

(1)求椭圆C的方程;

(2)若k1+k2=0,求m的值。

解析:(1)依题意得2a=4,所以a=2。,所以c=1,b2=a2-c2=3。

(2)椭圆的右焦点F(1,0)。设直线l:y=k(x-1)(k≠0),M(x1,y1),N(x2,y2)。联立方程组得(3+4k2)x2-8k2x+4(k2-3)=0,Δ＞0成立。所以因为0,所以,即y1·(m-x2)+y2(m-x1)=0。

所以k(m-x2)(x1-1)+k(m-x1)·(x2-1)=0恒成立。因为k≠0,所以(m+1)(x1+x2)-2x1x2-2m=0,即(m+1)·-2m=0,化简得8k2(m+1)-8(k2-3)-2m(3+4k2)=0,解得m=4。

五、椭圆中的存在性问题

例5 已知椭圆的离心率,右焦点F到上顶点的距离为点C(m,0)是线段O F上的一个动点。

(1)求椭圆的方程。

(2)判断是否存在过点F且与x轴不垂直的直线l与椭圆交于A,B两点,使得并说明理由。

(2)由(1)得F(1,0)。由题意知0≤m≤1。假设存在满足题意的直线l,设l的方程为y=k(x-1),由

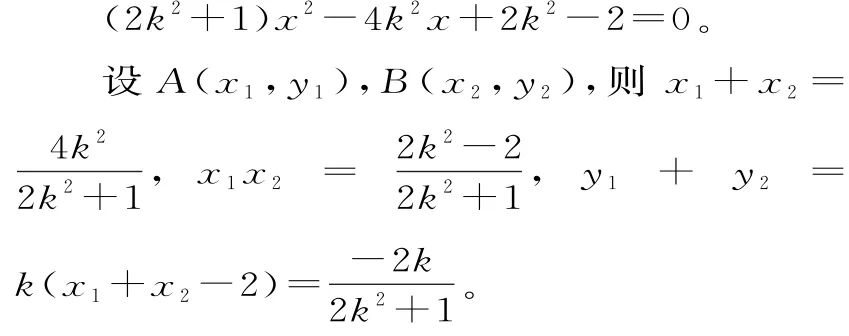
点评:本题主要考查圆锥曲线的知识。第一问,根据题意解出a、b、c,即可求得椭圆的方程。第二问,假设存在满足题意的直线代入椭圆方程,由分类讨论可顺利求解。

追踪:(2 0 1 9届厦门市湖滨中学高三理科数学第一次质检卷)椭圆＞b＞0)的左焦点为F1,右焦点为F2,离心过F的直线交椭圆于A、B两点1且△A B F2的周长为8。

(1)求椭圆E的方程。

(2)设动直线l:y=k x+m与椭圆E有且只有一个公共点P,且与直线x=4相交于点Q。试探究:在坐标平面内是否存在定点M,使得以P Q为直径的圆恒过点M?若存在,求出点M的坐标;若不存在,说明理由。

解析:(1)因为|A B|+|A F2|+|B F2|=8,所以|A F1|+|A F2|+|F1B|+|B F2|=8,4a=8,a=2。

因为动直线l与椭圆E有且只有一个公共点P(x0,y0),所以m≠0且Δ=0,即6 4k2m2-4(4k2+3)(4m2-1 2)=0,化简得4k2-m2+3=0。(*)

假设平面内存在定点M满足条件,由图形对称性知,点M必在x轴上。设M(x1,0),=0对满足(*)式的m、k恒成立。因此,

故存在定点M(1,0),使得以P Q为直径的圆恒过点M。