基于多个系统因素控制图的预防维修决策模型研究*

白 桦，赵永强

(1.中国飞行试验研究院，西安 710089；2.西安邮电大学 现代邮政学院，西安 710061)

0 引言

制造企业需要考虑其资源的规划与使用效益，从制造过程的角度提高产品质量、降低生产成本、缩短生产周期、提高生产系统的稳定性及可靠性，这对实现制造业智能化、降低运营成本、增强企业产品竞争力有着重要支撑作用。智能制造是集成设备、技术及信息为一体的先进制造系统，对设备可靠性要求很高。设备维修支出已成为制造系统最大的单项支出费用，占到企业制造成本的15%～40%左右，如果能在过程控制的环节选择适当时机对设备开展预防维修活动，就能够在降低设备失效率的同时提高整体产品的质量水平，有效的降低总成本。因此，制造系统的质量控制需要考虑维修管理，这对提高产品质量、保障生产稳定、降低运营成本有重要的支撑作用。

1 模型构建的理论基础

有较多学者研究了控制图在设备预防维修决策方面的应用。国内方面，周广文等[1]分析了数控机床主轴变形数据特征，构建了基于均值极差控制图机床主轴预防控制模型，根据实时数据判断主轴是否存在故障，提高了机床的可靠性。李爱民等[2]以离合器的拉杆的维修数据建立了均值-极差控制图，结果显示控制图可以有效控制设备的维修过程。周源泉等[3]以可靠性为目标，构建了设备平均故障间隔期的控制图模型，它能评估出系统在使用中的可靠性，并能通过信息反馈控制产品在生产中的可靠性。赵永强[4]假设零备件的失效率服从指数分布,在参数已知的条件下构建出零备件的计数型控制图模型，控制图可对设备零备件的失效频次进行有效预防控制。国外方面，Yerel 等[5]开发了一个基于统计过程控制的预防维修决策模型，实际维修记录显示可以将其服务产出降低至少5%～10%。Zhao[6]假定设备失效密度函数服从威布尔分布，在设备失效密度函数服从威布尔分布的条件下构造R图，并给出一个例子来验证模型的有效性。Alsyouf 等[7]以卡车冷却系统为研究对象，设计了一个基于统计过程控制图的可修复系统故障时间监测模型，发现监测故障时间有助于发现和降低系统可靠性的恶化。

从文献综述可知，研究预防维修和控制图整合时都需要构建数学模型，最终使单位时间的损失成本最低，对设备的预防维修均考虑在过程失控后进行维修，此时的设备已经出现较严重的问题，会使维修难度增加，也会导致生产出的产品质量水平下降。因此，需要考虑在控制图中设定警戒区域，当控制图点落入此区域时，就对设备进行预防维修，这样就能够保证设备依然处于正常状态时就进行预防维修，进而保证生产的有效性和可靠性。

2 模型构建

2.1 模型假设

基本假设如下：

(1)X服从正态分布；

(2)多个系统因素会导致生产过程造成均值产生m次的偏移，偏移量为δmσ(m=1,2,3,...)；

(3)导致过程异常的各系统因素间是相互独立的；

(4)过程在任何时候都终始处于一种或两种状态，在控制界限内或在界限外，在初始期处于受控状态；

(5)过程控制的抽样样本量为随机，抽样间隔期为h小时；

(6)由于预防维修无法将生产过程由异常状态恢复到受控状态，因此假设预防维修的成本小于生产过程异常后修复的成本；

(7)假设生产过程为连续性生产，即控制图监测到系统因素并开始寻找与修复生产过程时，生产不停止；

(8)当产品特性超过控制边界的2/3时，对设备进行预防维修；模型的最终目标是在一个周期内运行周期最长，损失最小。

2.2 模型的构建

(1)模型的控制周期时间分析

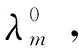
(1)

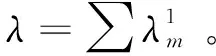
Pw=Φ(w)-Φ(-w)，Pr=2[Φ(k)-Φ(w)]

(2)

令h0为受控状态下每次抽样的期望间隔时间，即抽样时间间隔与预防维修时间的期望值之和，h为抽样时间间隔，Z为预防维修执行时间。则有：

h0=h×Pw+(h+Z)×Pr

(3)

由于生产过程发生异常的概率服从指数分布，因此生产过程在受控状态下的发生概率，即尚未发生异常的概率将随时间而递减，由上述每次抽样间之期望间隔时间来看，则其每次抽样间隔过后生产过程的发生概率分别为e-λh0，e-2λh0，e-3λh0，……，因此生产过程在受控状态到异常发生后首次抽样之前所经过的时间为受控状态的每次抽样间的期望间隔时间与每次抽样间隔过后生产过程发生概率的乘积总和，则有下式：

T0=h0e-λh0+h0e-2λh0+h0e-3λh0+…

(4)

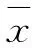
(5)

w为警戒界限系数，k为控制界限系数，则有：

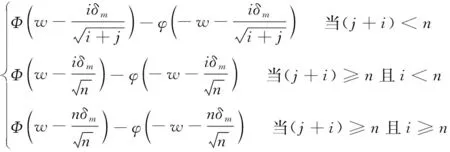
(6)

Pm,j,i=

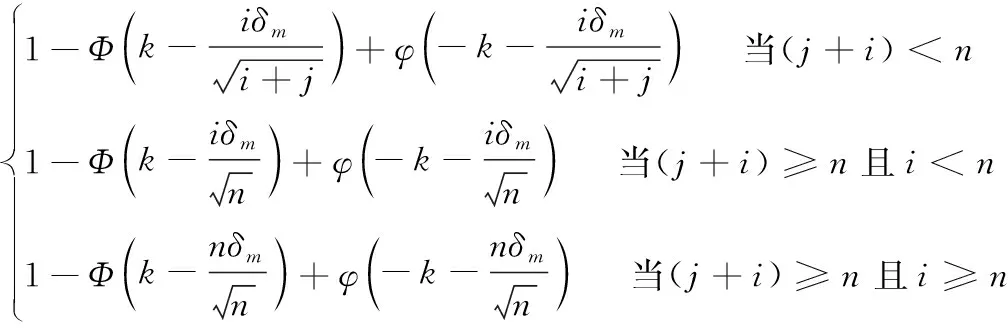
(7)

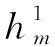
(8)

在第三种情况时，(j+i)≥n且i≥n，Pm,j,i与j或i无关；此时Pm,j,i=Pm,j,n=Pm且Qm,j,i=1-Pm=Qm。在以上三种情况下，当j≥n时，Pm,j,i=Pm,n-1,i。当第m次异常发生在(s,s+1)间时，样本量的期望为：

Em,s=Pm,s,1+2Qm,s,1Pm,s,2+3Qm,s,1Qm,s,2Pm,3+…

(9)

第m次异常发生后的平均运行时间ARLm为：

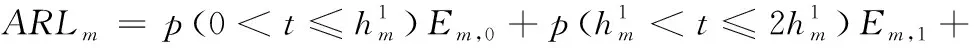
(10)

(11)

整个过程最后异常发生后至控制图监测出异常的时间为T1：

(12)

在一个周期内第m异常发生的平均时间为τm：

(13)

令e为单位产品的抽样与检验时间，Dm为第m异常发生后过程的修复时间。总的周期为E(T)：

(14)

(2)模式分析

一个周期内的过程期望的损失成本的构成包括：

1)如果Am因素发生，假定Um为第m异常状态下的单位时间损失成本，那么对于差的质量期望损失可以用下式表示：

(15)

2)Wm为第m异常发生后寻找异常来源与修复过程的成本，如果Am因素发生，需要花费成本Wm去找出并修复这个系统因素，所以，找出并将失控过程状态转变为受控状态的损失成本为：

(16)

3)Cpm为每次预防维修活动的平均成本，预防维修成本可以表示为：

(17)

4)令α为过程处于受控状态时单一因素落于控制界限以外的发生概率，在一个周期内假警报次数的期望值NFA与α及受控状态内取出的样本量的期望值相关，NFA可用下式表示：

(18)

这里α=2[Φ(-k)]，当过程处于受控状态时每次假警报的平均成本为V，因此，每个周期内发现假警报的期望成本为：

C4=NFA·V

(19)

5)令fc为处理样本容量无关的单个样本成本，vc为抽样、监测、分析及描点单个样本的变动成本，每个样本都会在控制图上描点，所以，单位时间维护控制图的成本为：

(20)

在一个平均周期过程的单位时间损失成本则可以表示为：

E(TC)=(C1+C2+C3+C4)/E(T)+C5

(21)

对模型分析的目的在于找出参数n、h、k，使整个单位时间损失成本最小。由于E(TC)是一个非常复杂的、关于决策变量n、h、k的函数，这些参数的初始数值通过指定的方式来获得整个单位时间的损失成本，通常可以利用Matlab软件进行分析。

3 算例分析

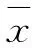
表1 相关参数分析

通过计算可知，最优的控制图参数n=2、h=0.5523、k=2.8543，此时单位时间的损失成本为399.41，此时的成本最低。令r=1、Z=1、Cpm=0，意味着控制图模型并不考虑设备的预防维修，保持n=2、h=0.5523、k=2.8543不变，发现单位时间的损失成本为459.33，说明控制图模型考虑预防维修能使控制图单位时间的损失成本下降。由此可知，利用控制图模型进行预防维修决策对降点总成本是有用的。

4 结论

以均值控制图经济性模型为基础，假设会有多个系统因素影响控制图的过程质量，在控制图变量中增加预防维修的成本及时间，以单位时间损失函数为目标函数，假设样本落于控制图警戒区域时就执行预防维修决策，构建了基于多重系统因素均值控制图的预防维修决策模型。利用软件对构建模型进行了参数分析，发现随着Am次数的增多，Um值增加而Wm及Dm值在下降。算出控制图单位时间损失成本最小时的控制图参数值参数n、h、k，在这些参数不变的情况下假设控制图不考虑设备预防维修，发现此时的单位时间损失成本会增加，说明在控制图警戒区域出现报警就执行预防维修能够降低总成本。由此可见，利用控制图来进行设备预防维修决策是可行的。