基于T-S模糊故障树的刀架系统可靠性分析

陈 乐，王贤琳，李卫飞，王 恺，刘凯乐

(武汉科技大学 a.绿色制造工程研究所；b.冶金装备及其控制教育部重点实验室；c.机械传动与制造工程湖北省重点实验室，武汉 430081)

0 引言

数控车床的刀架系统对于车床系统可靠性水平影响显著，成为了制约我国机床可靠性发展的关键环节[1-2]。

传统的故障树分析(Fault tree analysis，FTA)方法应用广泛，但仍有不足[3-5]。①对于复杂系统而言，FTA难以准确地描述部件间的事件联系；②部分机床零部件故障频率较低，很难获取大量的统计数据；③FTA描述事件时基于布尔运算和概率运算，且多为二态系统。

针对上述问题，Tanaka等[6]首次将模糊理论应用在FTA中，从而解决了FTA中基本事件故障率模糊以及事件间联系的不确定性问题，但是其方法还停留在布尔运算的逻辑上。张龙等[7-8]提出并证实将模糊算法引入FTA中能够有效解决失效概率的模糊性和不确定性问题，但其依然采用传统的逻辑门。宋华等[9]运用T-S模糊逻辑门来表达部件间的联系，有效地解决了故障机理不确性定问题。

针对上述问题，本文以某机床的刀架系统的可靠性分析为例，建立了刀架系统顶层事件与底层事件之间的多态故障模型，将事件连接的不确定性问题转化为定量问题，结合T-S模糊重要度分析了影响顶层事件故障概率的关键环节，为后续可靠性改善提供一定的参考依据。

1 T-S模糊故障树

T-S模糊模型由一系列的IF-THEN模糊规则组成，运用T-S门规则来描述事件之间的联系，用模糊数来代替FTA中的布尔代数，以及运用事件的模糊子集表示失效的可能性概率，进而求解顶事件的失效可能性模糊子集[9-10]。

为了表达部件的故障程度，引入模糊代数来表达底层事件的故障程度，如表1所示。

表1 故障程度模糊代数

其中模糊数的隶属度函数描述为梯形隶属函数，梯形隶属度函数F可以表示为：

F=(F0，sl，ml，sr，mr)

(1)

式中，F0为模糊数支撑集的中心，sl和sr为左右支撑半径，ml和mr为左右模糊区。F0为隶属函数F所描述的模糊数中间值。

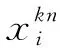
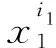
(2)

那么，上级事件处于不同故障状态的失效可能性分别为：

(3)

2 T-S模糊故障树重要度

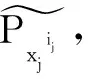
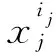
(4)

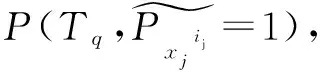
定义: 部件对顶事件T 为Tq的T-S模糊重要度为：

(5)

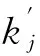
3 实例分析

3.1 T-S模糊故障树分析

本文选取某型号的数控车床的刀架系统进行分析，该刀架系统由刀盘系统、电气系统以及检测系统组成，其各子系统部件组成及其故障率如表2所示。

表2 刀架系统各部件组成及其故障率

通过查阅相关文献[1-2]以及专家调查，根据表2信息建立以刀架系统为顶事件的T-S模糊故障树模型来分析其系统可靠性如图1所示。其中，事件Y={y1，y2，…，y5}代表子系统，事件X={x1，x2，…，x10}代表组成系统的各子部件。T-S门1～门5均为T-S模糊故障树门逻辑。假设x1，x2，…，x8和y2，y3，y4，y5的常见故障程度为(0，0.5，1)，其隶属度函数选为sl=sr=0.1，ml=mr=0.3，x9，x10，y1的常见故障程度为(0，1)，其隶属度函数选为sl=sr=0.25，ml=mr=0.5。其中T-S模糊门规则如表3～表7所示。

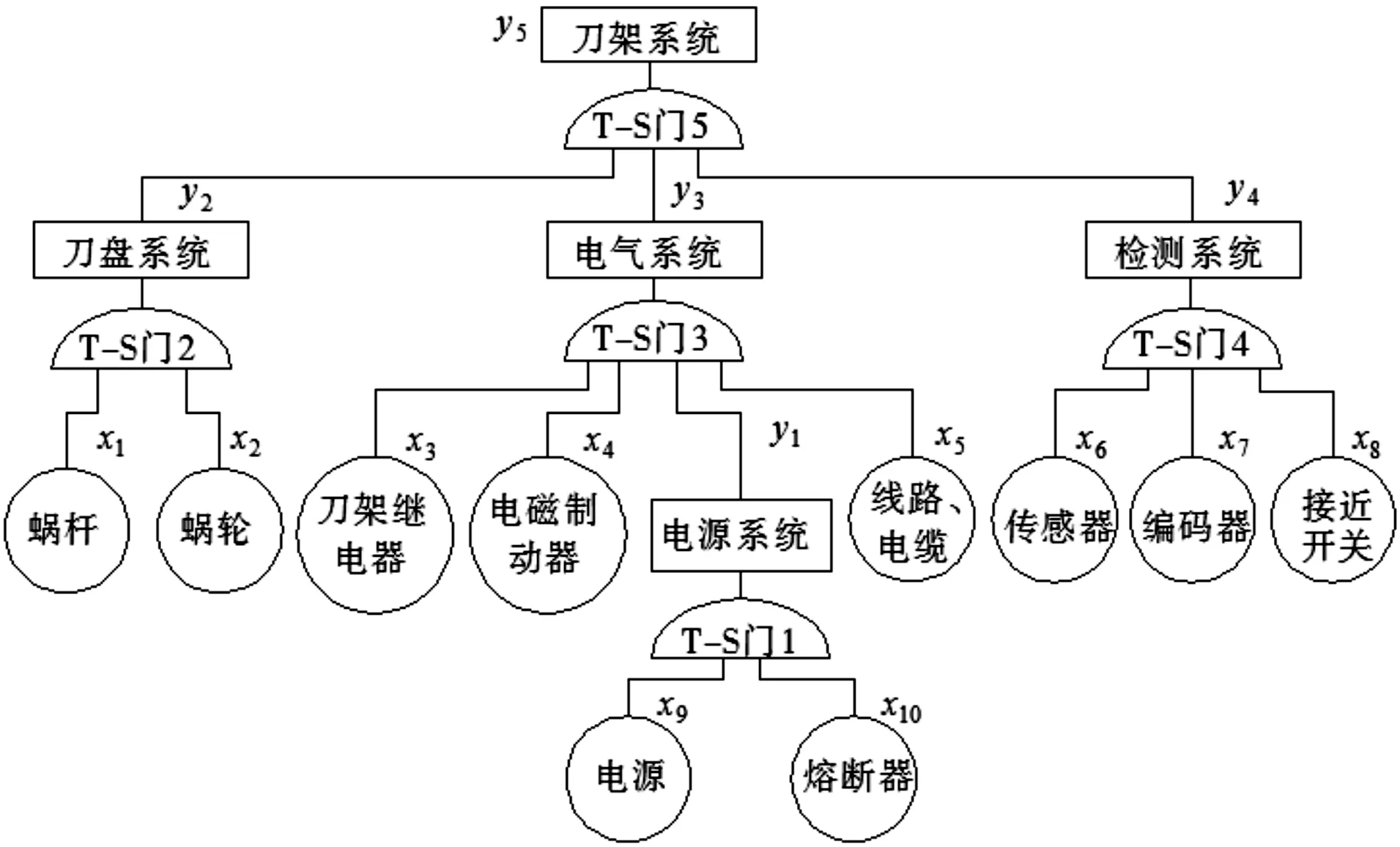
图1 刀架系统T-S模糊故障树分析

规则x9x10y10110010201013100141101

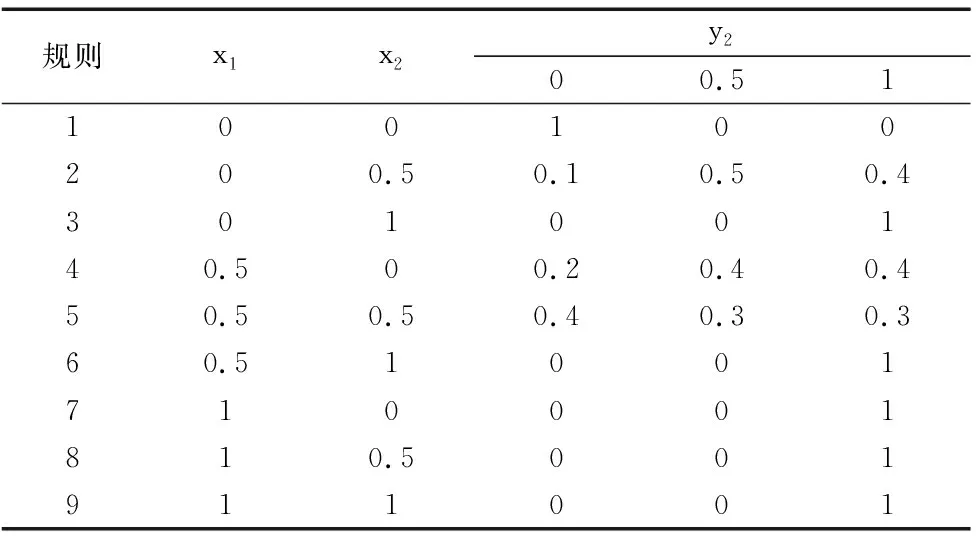
表4 T-S模糊门2

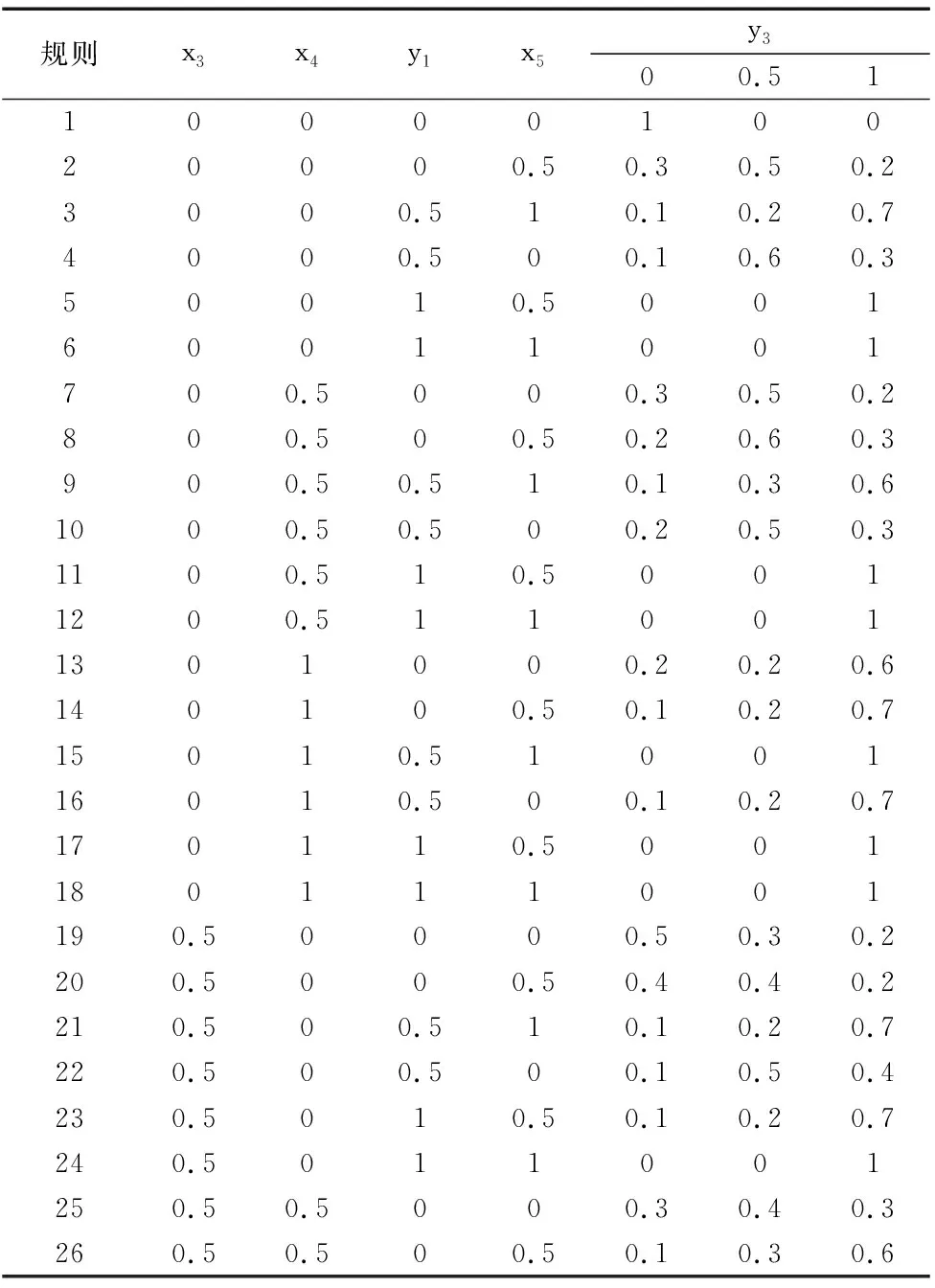
表5 T-S模糊门3

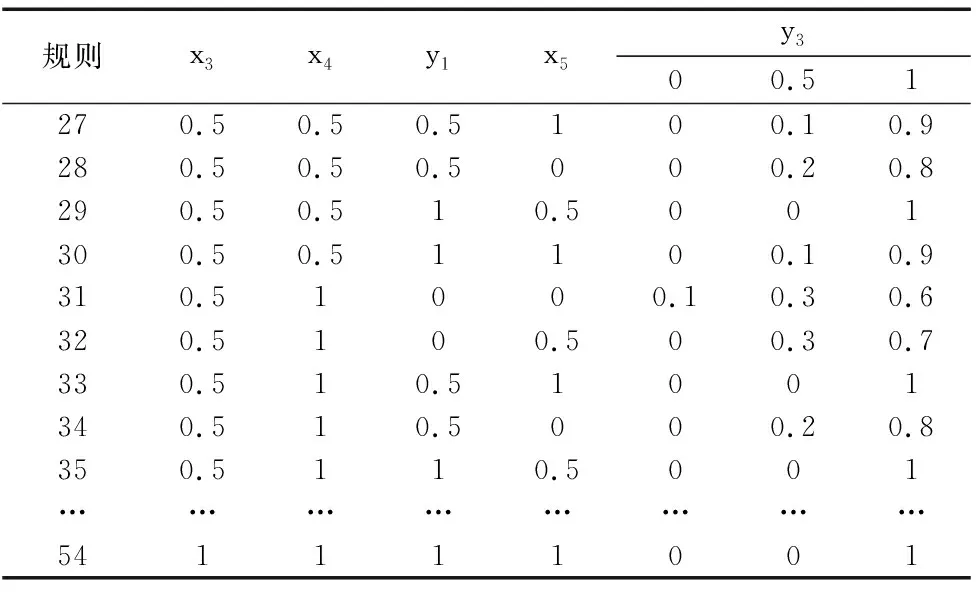
续表

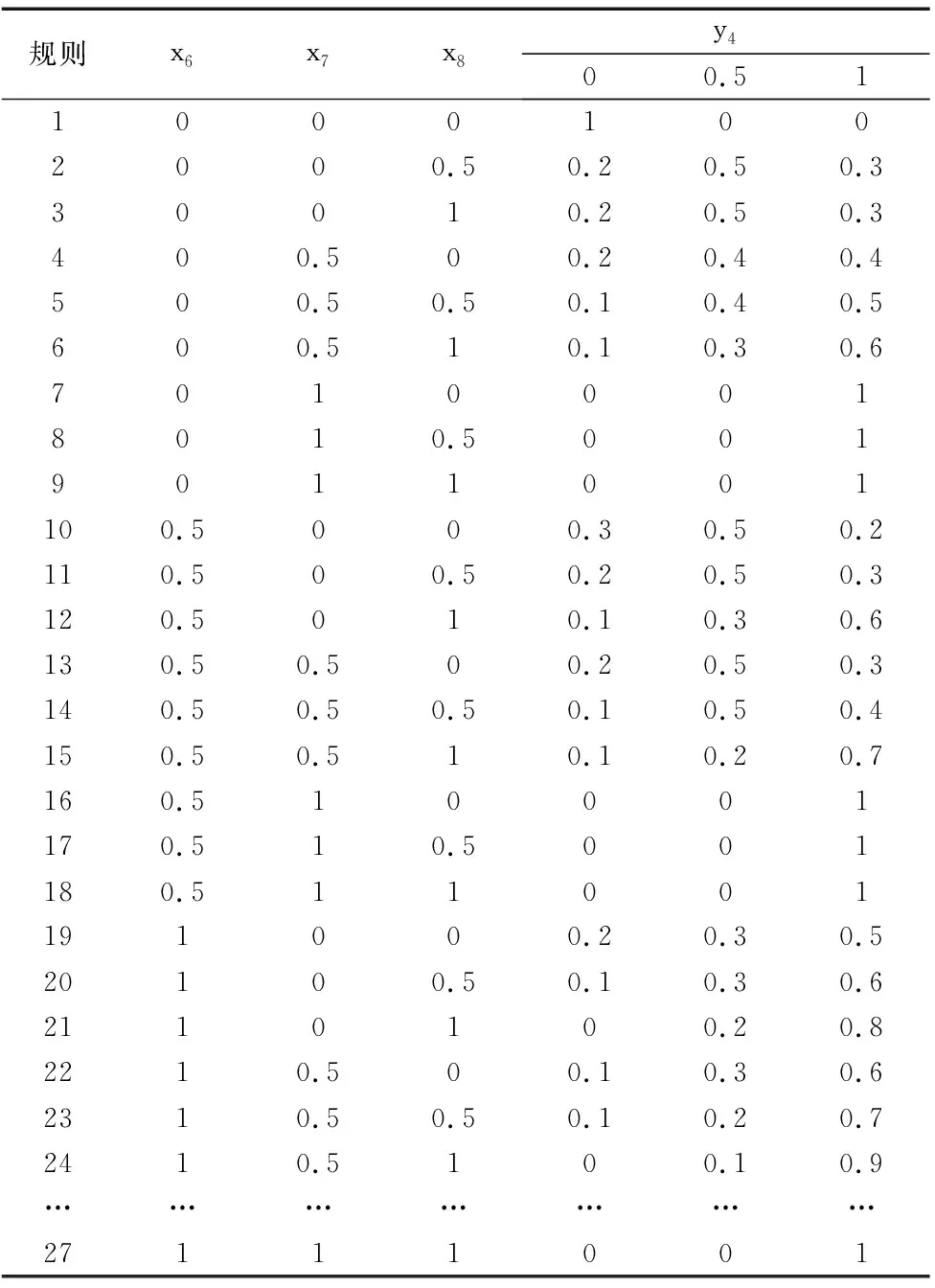
表6 T-S模糊门4

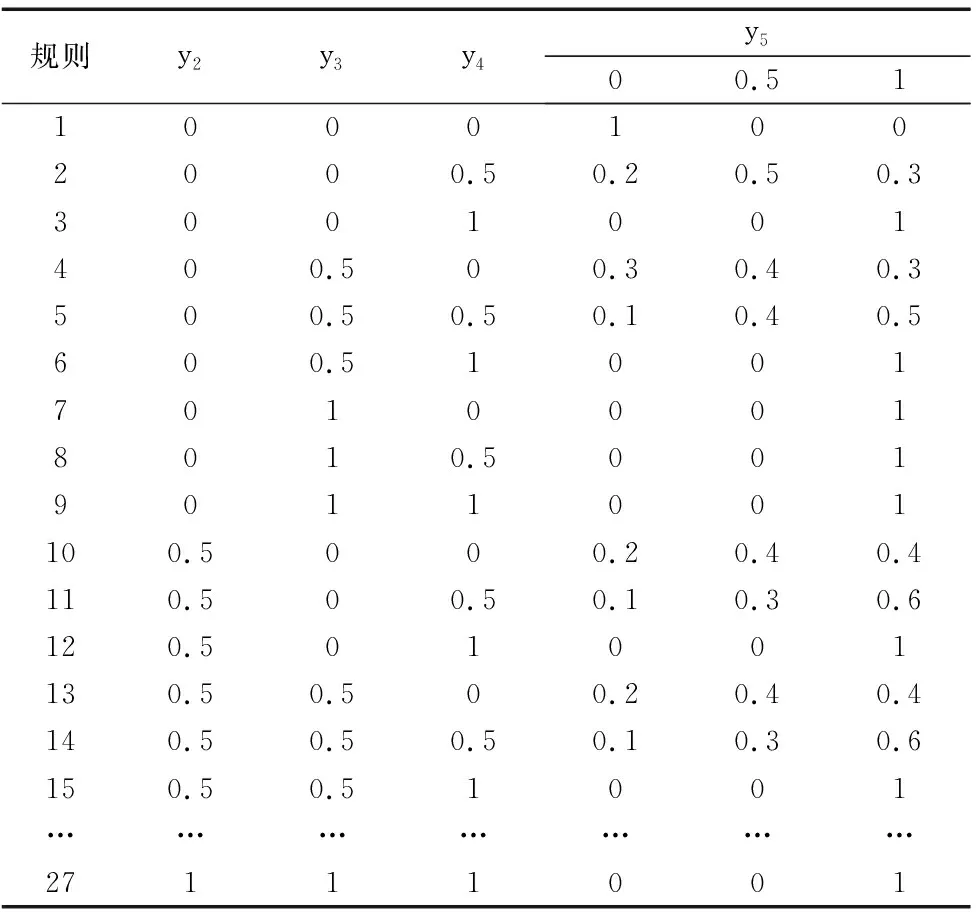
表7 T-S模糊门5

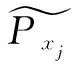
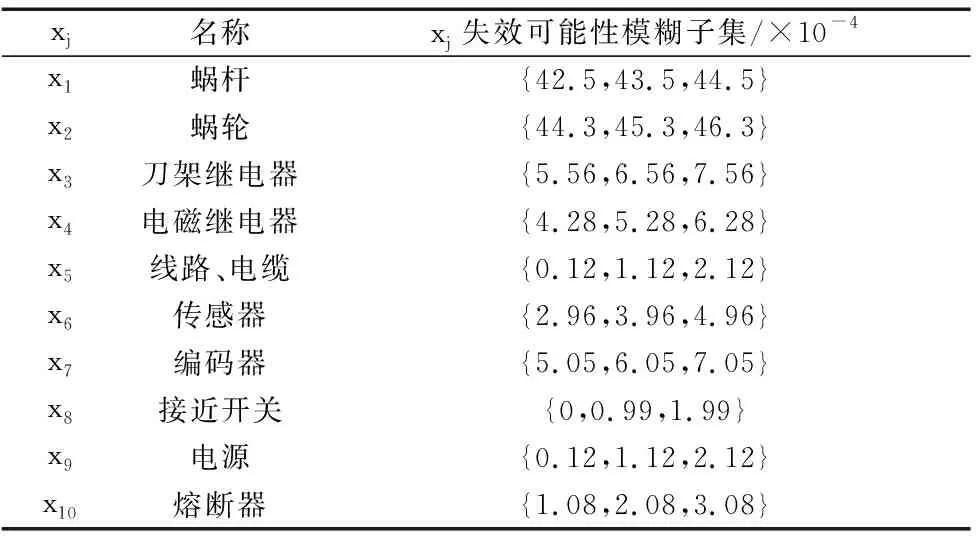
表8 部件故障状态为1时的失效可能性模糊子集

表7的中的数据给出了事件X={x1，x2，…，x10}故障状态为1时的模糊可能性。若X={x1，x2，…，x8}故障状态为0.5的概率数据与1相同，则根据表3～表7的T-S门规则，结合式(2)、式(3)计算得出事件Y={y1，y2，…，y5}的失效可能性模糊子集如表9所示。

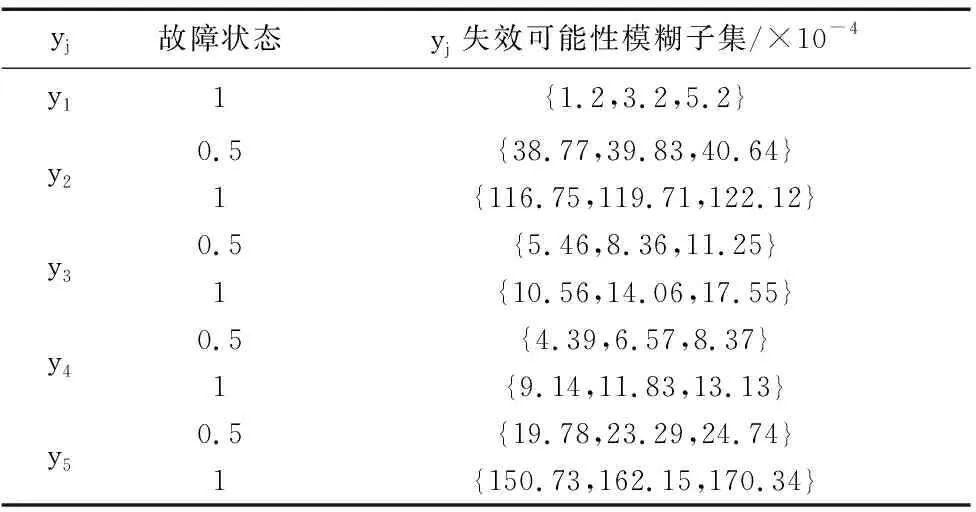
表9 y1～y5失效可能性模糊子集

3.2 T-S模糊重要度

利用公式(4)，得出部件x1故障状态为1对y5为0.5的T-S模糊重要度为：

同理可以得到各部件故障状态为0.5和0时的T-S模糊重要度见表10。

表10 各部件故障状态的模糊重要度

根据表10，已知部件x1故障状态为0.5和1时的T-S模糊重要度，利用公式(5)，得到x1对y5的故障状态为0.5时的T-S模糊重要度为：

同理，可得到其他部件对y5故障状态为0.5和1时的模糊重要度如表11所示。

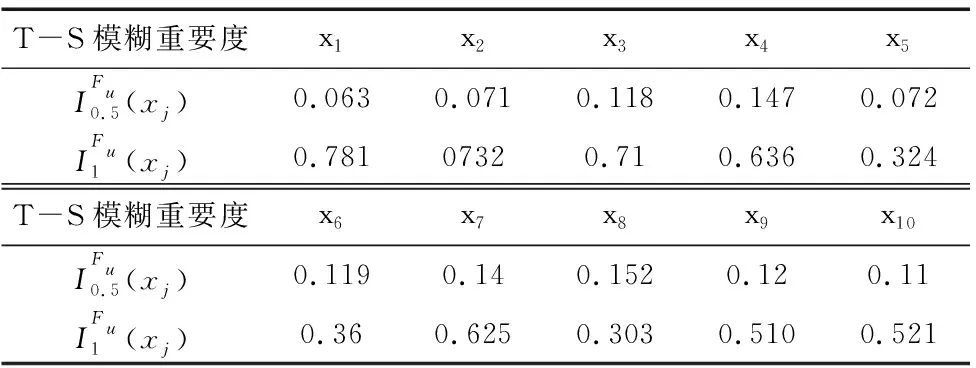
表11 各部件对于顶事件故障状态模糊重要度

在已知部件故障状态的失效可能性的模糊子集的情况下，由表11可得，当系统处于半故障时，部件x8对刀架系统故障率影响最大，其影响大小依次为：x8>x4>x7>x9>x6>x3>x10>x5>x2>x1；当系统处于完全故障状态时，部件x1对刀架系统故障率影响最大，其影响大小依次为：x1>x2>x3>x4>x7>x10>x9>x6>x5>x8；上述结果与文献[1]中的结论相同，刀盘系统是刀架系统的薄弱环节，应当给予重点关注。

4 结论

本文应用T-S模糊故障树模型分析了刀盘系统T-S门逻辑关系，使用模糊故障概率求解其顶事件的模糊故障概率，并分析了不同故障状态下的底层事件对于顶事件的模糊重要度。该方法可解决刀架系统故障数据缺失和多源异构问题，且能克服传统故障树只能对二态系统进行分析的局限，找出了影响系统可靠性的薄弱环节，可为刀架系统的检修和故障诊断提供参考。