全国名校双曲线拔高卷（A 卷）答案与提示

一、选择题

1.A 2.A 3.D 4.B 5.C 6.D 7.A 8.C 9.A 10.A 11.D 12.A 13.A 14.C 15.D 16.C 17.C 18.D 19.D 20.C 21.C 22.A 23.A 24.C 25.D 26.A 27.B 28.A 29.B 30.C 31.A 32.C 33.D 34.D 35.C 36.A 37.B 38.D 39.C 40.A

二、填空题

三、解答题

又c2=a2+b2=48,可解得a2=36,b2=12。

故可设双曲线的方程为x2-3y2=λ(λ

因为c2=a2+b2,所以a2=b2。

可设双曲线方程为x2-y2=λ(λ≠0)。

故双曲线的标准方程为x2-y2=6。

62.(1)设点P(x0,y0),由题意知双曲线的两条渐近线方程分别为x-2y=0和x+y=0。

则点P(x0,y0)到双曲线的两条渐近线的距离分别为

63.(1)依题意可设双曲线的标准方程为:

因为A1、P、M三点共线,所以(x+3)y0

64.(1)由已知得|P F1|=|P F2|+2,即|P F1|-|P F2|=2,所以点P的轨迹C为双曲线的右支,且2a=2,a=1,|F1F2|=2c=4,c=2。

(2)当直线l1的斜率不存在时,A(2,3),则直线BM经过点E(1,0);

当直线l1的斜率存在时,不妨设直线l1:y=k(x-2),A(x1,y1),B(x2,y2)。

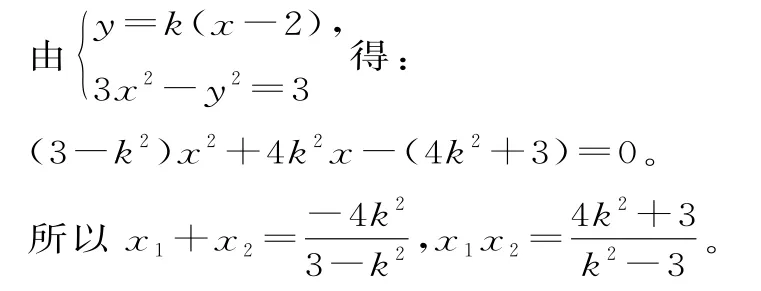
由y1=k x1-2k,y2=k x2-2k,整理得恒成立。

因此,kEM=kEB,BM经过点E(1,0)。

故直线BM过定点(1,0)。

因为-3k2-7＜0,所以1-3k2＜0,k2＞

解得a=1。

b2=2-1=1。

故双曲线E的方程是x2-y2=1。

由题意可得方程有两个负数根,则:

(3)由题意及(2)得:

整理得2 8k4-5 5k2+理2=0。

设C(x0,y0),由得

当m=-4时,所得的点在双曲线的右支上,不合题意。

因此,m=4。