全要素生产率、资产市场扭曲与中国通胀-产出动态关联性

蒋 涛

(西南财经大学 中国家庭金融调查与研究中心，四川 成都 610074)

一、问题提出

通货膨胀率和产出波动是名义经济和实际经济波动中的两个关键变量，它们的动态关联性是货币经济波动中的典型特征事实之一。库利和汉森(Cooley & Hansen，1995)[1]、沃尔什(Walsh，2017)[2]概括了美国经济中通货膨胀率和产出波动的动态关联性，而且梳理了将二者联系起来的货币经济周期理论，比如信息摩擦、有限参与、价格粘性和工资粘性等。对于中国经济中通货膨胀率和产出波动的动态关联性，刘金全和谢卫东(2003)[3]、刘金全和刘志刚(2005)[4]、周文和赵果庆(2012)[5]进行了总结。然而，多数文献研究通货膨胀率和产出对各种经济冲击的反映，而少有文献对这种动态关联性进行解释。欧阳志刚和王世杰(2009)[6]、黄桂田和赵留彦(2010)[7]、陈守东等(2014)[8]通过估计结构向量自回归模型，识别通货膨胀率和产出对货币冲击、供给冲击、需求冲击等各种经济冲击的反应。许伟和陈斌开(2009)[9]、李春吉等(2010)[10]、王君斌(2010)[11]则在动态随机一般均衡模型框架下，通过引入银行信贷、价格粘性、垄断竞争等经济摩擦变量，解释通货膨胀率和产出对各种冲击的反应。相对于通货膨胀率和产出对各种经济冲击的反应，它们的动态关联性是更为基础的需要解释的特征事实，因为前者需要事先假设识别条件。此外，现有文献提出的各种货币经济周期模型能在多大程度上产生与实际数据一致的通胀-产出动态关联性，也是判断它们在多大程度上适合中国的重要标准。

本文在货币经济模型中应用查里等(Chari et al.，2007)[12]提出的商业周期报告(business cycle accounting，BCA)方法来分析上述问题。BCA方法的原理是将观测到的经济波动分解为各种楔子的波动，而具体经济周期模型中经济冲击和经济摩擦对应于这些扭曲模型均衡条件的楔子。这样，各种经济冲击和经济摩擦，如果对应于对观测到的经济波动最具解释力的楔子，就能更好地解释经济波动。查理等(2007)[12]将BCA方法应用到美国经济，发现在效率楔子、劳动楔子、投资楔子和政府消费楔子等四种楔子中，效率楔子和劳动楔子对美国经济波动最具解释力。布林卡等(Brincaet et al.，2016)[13]进一步将BCA方法应用到经济合作与发展组织(OECD)国家，发现对于不同的OECD成员体，最具解释力的楔子不尽相同，但基本都是效率楔子和劳动楔子或者和投资楔子的组合。高(Gao，2007)[14]、何等(He et al.，2009)[15]、蒋涛(2013)[16]将BCA方法应用到中国经济，都发现效率楔子的重要解释力。然而，这些文献只考虑真实经济的波动，而忽视名义经济的波动。舒斯特克(ustek，2011)[17]将BCA方法扩展到货币经济模型，还引入资产市场楔子和货币政策楔子，以便分析通货膨胀率和名义利率与产出波动的动态关联性。这种扩展的BCA方法被布林卡(Brinca，2013)[18]、乔和李(Cho & Rhee，2015)[19]用来研究经济波动或者货币政策。本文基于舒斯特克(2011)[17]的货币经济模型来分析中国通货膨胀率和产出波动的动态关联性。

二、模型与楔子

本文使用一个包含名义债券、名义价格和名义利率等名义变量的简单货币经济模型。除效率楔子、劳动楔子、投资楔子和政府消费楔子外，该模型还引入资产市场楔子和货币政策楔子。这些外生楔子是模型中产出、要素投入和通货膨胀率等变量发生波动的来源，也是共同产生通胀-产出动态关联性的六种因素。各类楔子衡量模型中竞争性均衡条件受到的各种扭曲，代表经济波动中不同类型的冲击传导机制。具体的经济冲击和经济摩擦分别对应于不同的楔子。

(一)模型的设定

模型由代表性家庭的决策行为、代表性厂商的决策行为和货币政策规则三部分组成。

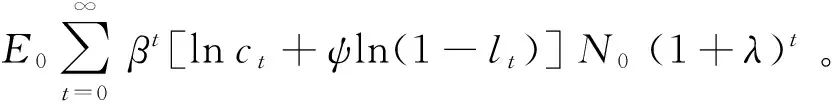
(1)

其中，Rt是债券的名义利率，pt是单位产品的名义价格，wt是真实劳动工资，rt是真实资本租金，Tt是政府转移支付，δ是资本折旧率。名义债券bt为一期债券，在t+1期将支付利率为Rt的回报。这种引入债券的方式在麦克葛兰特(McGrattan，2001)[20]、爱尔兰(Ireland，2004)[21]等的研究中被使用。投资楔子τxt如同对投资征税，资产市场[注]这里使用资产市场的概念而不是资本市场的概念，原因是前者比后者更具一般性。资本市场一般特指股票、债券等中长期金融资产的交易，但不包含国库券、商业票据等短期金融资产的交易。因此，资产市场的概念更加宽泛。楔子τbt如同对名义债券征税，而劳动楔子τlt如同对劳动收入征税。

代表性厂商选择资本kt和劳动lt以最大化t期利润πt，πt=yt-rtkt-wtlt。代表性厂商面临的约束条件为：

yt=Atktα[(1+γ)tlt]1-α

(2)

其中，At为效率，yt为产出，α为资本收入份额，γ为劳动增强型技术进步增长率。

货币政策工具是名义利率Rt。货币政策设定参考泰勒(Taylor，1993)[22]的研究，表示为如下反馈规则：

(3)

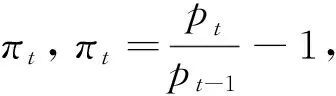
联合代表性家庭和代表性厂商各自最优化问题的一阶条件，就可以得到下列等式：

(4)

(5)

(6)

模型均衡条件除式(1)—式(6)，还包括下面的资源约束条件：

ct+xt+gt=yt

(7)

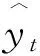
(二)楔子的含义

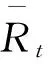
经济波动理论提出各种具体经济冲击和经济摩擦。虽然每种理论都提供一种冲击传导机制，但是它们的波动效果是通过扭曲模型均衡条件实现的，等价于扭曲性楔子的波动效果。因此，每种楔子代表一种类型的冲击传导机制，而具体经济周期模型中的冲击和摩擦对应于不同的楔子。有学者给出一些例子，用来说明导致劳动、资本等生产要素在不同企业部门间配置不当的就业规则、劳动力市场政策、企业政策等经济冲击和摩擦，扭曲总产出函数中的全要素生产率，对应于效率楔子。货币冲击和粘性工资，扭曲消费和闲暇的替代，对应于劳动楔子。金融加速器、投资专属技术变迁，扭曲投资决策，对应于投资楔子。货币冲击和粘性价格，扭曲消费和闲暇的替代、投资决策，对应于劳动楔子和投资楔子。中央银行目标通货膨胀率的变化，扭曲货币政策，对应于货币政策楔子。特别地，货币政策冲击可以对应于效率楔子，如布埃拉和莫尔(Buera & Moll，2015)发现信贷紧缩冲击经过具有异质性全要素生产率的企业的信贷抵押约束的传导，转化为对总量生产函数中全要素生产率的负向冲击[25]。此外，货币供给量的冲击经过资产市场有限参与的传导，会对名义资产产生征税的效果，扭曲家庭的资产配置行为[26]。这种货币政策的冲击传导机制对应于资产市场楔子。

三、测量楔子

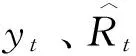
(一)数据与参数

本文主要用到1978—2016年的季度数据。按支出法核算的产出、居民消费、投资、政府消费和净出口的季度数据，不能直接获得，本文通过对年度数据进行插值来产生相关数据[注]虽然按生产法核算的产出、固定资产投资完成额、净出口、财政支出、社会零售品销售总额等季度数据可以获取，但是，这些数据并不是按照支出法核算的，如果直接使用，可能会产生较大的偏差。此外，这些数据开始于二十世纪九十年代，时序长度也不够。为保持与模型的口径一致，本文统一地对按支出法核算的产出、居民消费、投资和政府消费的年度数据进行插值，以获得跟模型口径一致的季度数据。。将国家统计局公布的按支出法核算的产出及其组成的数据，换算成按1997年不变价格计算并按15～64岁劳动人口数平均的真实人均数据，将三大产业的就业人数[注]1991年以后的就业人数来自国家统计局，1990年以前的就业人数来自霍尔茨(Holz，2005)[27]。分别乘以各产业每年的工作小时数[注]各产业工作小时数来自中国家庭金融调查2015年数据。其中，第一产业单位劳动力的年工作时间为2 140小时，第二产业为2 294小时，第三产业为2 247小时。这里使用各产业单位劳动力的年工作时间，主要是为了反映不同产业间单位劳动力工作时间的差异，以便更准确地衡量由于产业间就业结构的周期性变化所造成的劳动投入波动。，再除以劳动人口数和每人每年5 000小时的可用时间数，就得到人均劳动投入。对人均产出、消费、投资、政府消费支出[注]这里的政府消费支出是政府消费和净出口之和。和劳动投入的年度数据进行插值，就得到它们的季度数据。用居民消费价格指数作为通货膨胀率数据。利用国家统计局公布的原始数据，先将月度同比的居民消费价格指数转换为月度环比数据，再加总得到季度数据，最后用X12方法进行季节性调整。依据中国人民银行公布的历次利率调整数据和《中国金融年鉴》中的数据，可以得到各个季度的三月期存贷款基准利率，对每个季度取存款基准利率和贷款基准利率的均值以作为名义利率数据。

模型中其他参数或者通过校准得到，或者参考相关文献。主观贴现因子β取值(0.95)1/4，时间配置参数ψ取值1.8，资本折旧率δ取值1-(1-0.1)1/4，资本收入份额α取值0.5[注]前两个参数的校准参考了蒋涛(2013)[16]，后两个参数的校准参考白等人(Bai et al.，2006)[28]。。劳动增强型技术进步增长率γ是用对数产出对常数和时间回归得到的，取值0.02。人口增长率λ是用对数劳动人口数对常数和时间回归得到的，取值0.001 6。有学者研究了中国的货币政策规则。其中，郑挺国和刘金全(2010)除基本泰勒规则外，还估计了可变目标通货膨胀率、“活性”区制和“惰性”区制的货币政策规则[29]。本文主要采用他们对基本泰勒规则估计的参数，即名义利率对产出波动的调整参数ωy，取值1.122；名义利率对通货膨胀率波动的调整参数ωπ，取值0.389 9；利率平滑参数ρR，取值0.963 6。对其他货币政策规则估计的参数，将在后面用来进行稳健性检验。

(二)楔子的波动特征

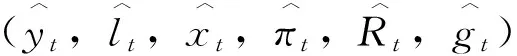
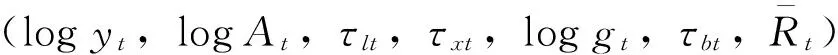
四、模拟实验

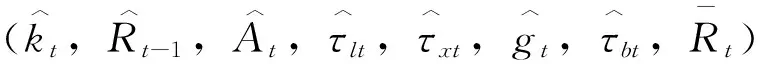
(一)楔子波动与产出波动

通过单个楔子波动的实验，可以分析各个楔子波动对产出波动的影响。图1给出模拟数据与实际数据(经过HP滤波)的比较。表1给出模拟数据的波动特征。效率楔子模拟的产出波动最接近实际产出波动。效率楔子模拟产出波动的相对标准差为1.12，与同期实际产出波动的相关系数为0.90。劳动楔子、投资楔子和政府消费楔子各自模拟的产出波动性明显小于实际数据，与实际数据的相关性也不明显。它们各自的相对标准差分别为0.34、0.31和0.43，各自与同期实际产出的相关系数分别为-0.57、0.57和-0.13。资产市场楔子波动或货币政策楔子几乎没有产生产出波动[注]这与模型设定中假设的结果是一致的。。这表明效率楔子波动对产生产出波动是最重要的。

图1 楔子模拟产出的波动与实际产出波动

表1 楔子模拟产出的波动特征

(二)楔子波动与通货膨胀率波动

通过单个楔子波动的实验，可以分析各个楔子波动对通货膨胀率的影响。图2给出模拟数据与实际数据(经过HP滤波)的比较。表2给出模拟数据的波动特征。资产市场楔子模拟的通货膨胀率，最接近实际通货膨胀率。资产市场楔子模拟的通货膨胀率，相对标准差为1.19，与同期实际通货膨胀率的相关系数为0.91。效率楔子、劳动楔子、投资楔子、政府消费楔子和货币政策楔子各自模拟的通货膨胀率，波动性明显小于实际数据，与实际数据的相关性也不明显。它们各自的相对标准差分别为0.12、0.05、0.12、0.10和0.00，各自与同期实际通货膨胀率的相关系数分别为-0.40、0.28、0.03、-0.28和0.10。这表明资产市场楔子波动对产生通货膨胀率是最重要的。

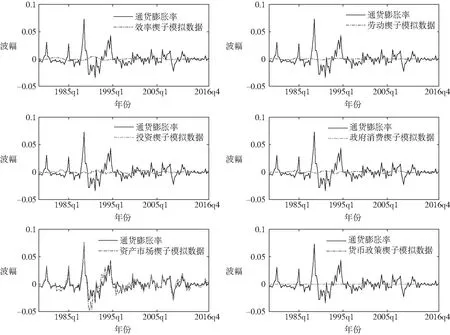
图2 楔子模拟的通货膨胀率与实际通货膨胀率

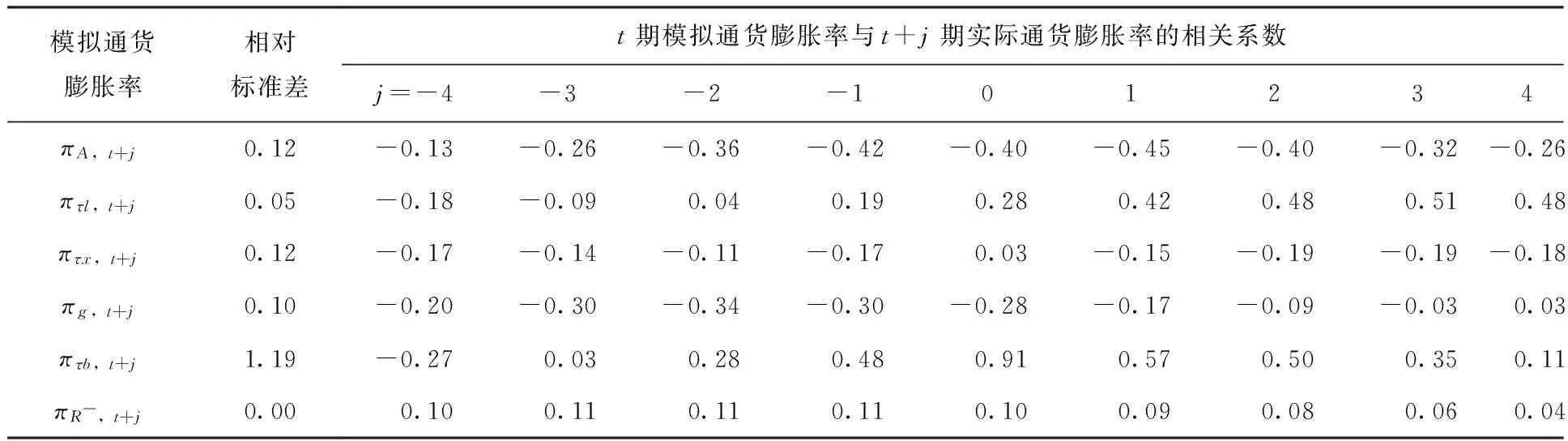
表2 楔子模拟通货膨胀率的波动特征

(三)楔子波动与通胀-产出动态关联性

首先，通过控制单个楔子波动的实验，可以分析它对产生中国通货膨胀率和产出波动的动态关联性的必要性。图3给出实际数据中通胀-产出(经过HP滤波)的动态关联性。通货膨胀率与各期产出波动(从过去五期到未来五期)的相关系数都大于0；其中，通货膨胀率和同期产出的相关系数在0.5左右。这表明通货膨胀率具有明显的顺周期性。通货膨胀率与过去产出和未来产出的相关系数，都随着期数的增加而逐渐减小；但是，通货膨胀率与未来产出的相关系数衰减得稍微慢一些。这表明通货膨胀率倾向于领先产出波动。在实验中，通过控制单个楔子的波动来产生实验数据，以分析这个楔子对产生这种动态关联性的必要性。实验结果由图3给出。如果劳动楔子、投资楔子、政府消费楔子和货币政策楔子中的一个被控制，那么通货膨胀率仍然主要表现出顺周期性以及稍微领先产出波动，通货膨胀率和产出波动的动态关联性基本不变。然而，如果效率楔子和资产市场楔子中的一个被控制，那么通货膨胀率表现出明显的逆周期性，而通货膨胀率和产出波动的动态关联性发生根本性变化。这组实验表明，效率楔子和资产市场楔子对产生中国通货膨胀率和产出波动的动态关联性的必要性，要远大于其他楔子。

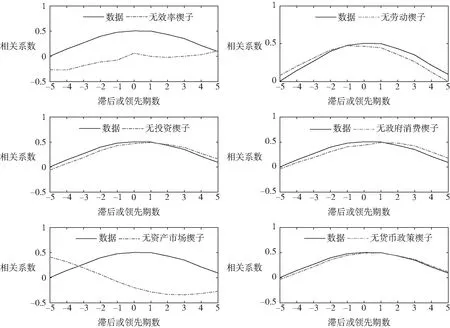
图3 楔子模拟的动态关联性与实际的动态关联性

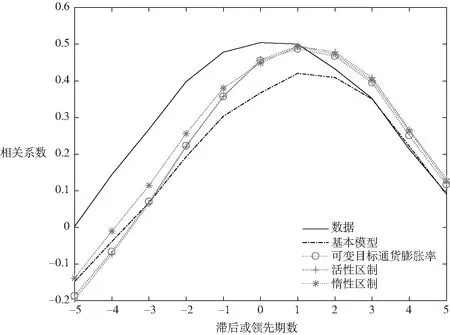
图4 货币政策规则与实验结果的稳健性

其次，通过效率楔子波动和资产市场楔子波动的实验，可以分析它们的组合对产生中国通货膨胀率和产出波动的动态关联性的充分性。实验结果由图4给出。如果仅考虑效率楔子波动和资产楔子波动，虽然通货膨胀率与同期产出和过去产出的相关系数比实际数据的小，但是通货膨胀率仍然是顺周期的并且稍微领先产出波动。实验数据的动态关联性与实际数据基本一致。

郑挺国和刘金全(2010)通过使用区制转移形式的泰勒规则，区分了中国货币政策规则中的可变目标通货膨胀率的货币政策规则、“活性”区制的货币政策规则和“惰性”区制的货币政策规则[29]。这些货币政策规则的差异体现为各种参数的不同，包括名义利率对产出波动的调整参数、名义利率对通货膨胀率波动的调整参数以及名义利率的平滑参数。为检验结果的稳健性，本文使用这些不同的参数设置来重新计算楔子并进行只有效率楔子波动和资产市场楔子波动的实验。结果由图4给出。与基本模型相比，通货膨胀率与同期产出和过去产出的相关系数有所增加，与未来产出的相关系数稍微大于实际数据。通货膨胀率仍然是顺周期的并且稍微领先产出波动。实验数据的动态关联性仍然与实际数据基本一致。

因此，效率楔子波动和资产市场楔子波动的组合，就足以产生与实际数据较为一致的通货膨胀率与产出波动的动态关联性[30-31]。即使考虑不同的货币政策规则，这种充分性仍然是足够的。

五、结论

本文通过在货币经济模型中应用BCA方法来分析中国通胀-产出动态关联性。在该货币经济模型中，通胀-产出动态关联性来自效率楔子、劳动楔子、投资楔子、政府消费楔子、资产市场楔子和货币政策楔子六种楔子。利用中国宏观经济数据，本文测量了中国经济中的这六种楔子。利用这些楔子的测量值，本文进行了模拟实验。结果表明：效率楔子对于中国产出波动至关重要，而资产市场楔子对于中国通货膨胀率波动至关重要；这两种楔子的组合就能产生足够的通胀-产出动态关联性。

这些结果意味着，那些将经济冲击和经济摩擦模型化为对全要素生产率和资产市场扭曲的货币经济模型，也许更适合中国的短期货币经济波动。已有研究在建立中国货币经济周期模型时，通常引入工资粘性、价格粘性或者金融加速器等经济摩擦。虽然它们是建立货币经济周期模型的经典方法，但是由于主要对应于劳动楔子或投资楔子，它们在解释中国通胀-产出动态关联性上不如效率楔子和资产市场楔子重要。因此，下一步的研究，可以考虑将各种经济冲击和经济摩擦模型化为对全要素生产率和资产市场的扭曲，比如在模型中引入在生产率上具有异质性的厂商和在名义资产市场只能有限参与的家庭。

这些结果也为制定货币政策提供新思路。促增长和防通胀是货币政策的两个重要目标。既然中国经济中通货膨胀率和产出波动的动态关联性主要来自于全要素生产率的波动和资产市场的扭曲，那么对于刺激增长而言，货币政策应该更加注重改善资源配置，对于预防通货膨胀而言，货币政策应该更加重视资产市场扭曲这个渠道。资源的优化配置一般引起全要素生产率的提升。由于中国经济中仍然存在一些资源配置不当[32]，应该通过差别化的利率政策或者信贷政策，将资源引导至那些更有生产效率的行业和企业。家庭对金融市场的参与受到限制，是对名义资产市场的一种扭曲。如果家庭不能及时将突然增加的货币转化为金融资产，那么将引起通货膨胀率的上升。因此，为减轻货币政策冲击通过名义资产市场的扭曲向通货膨胀传递，应该降低普通家庭参与金融市场的门槛，提供多元化的金融投资产品，让家庭能够更加灵活地配置金融资产。