中低速磁浮系统起浮阶段的振动特性分析

陆海英 韩霄翰 李忠继 何 翔 刘开成 陈志贤

1.中车长春轨道客车股份有限公司，长春，1300622.西南交通大学牵引动力国家重点实验室，成都,6100313.中铁二院工程集团有限责任公司，成都，6100314.中铁第四勘察设计院集团有限公司，武汉，430063

0 引言

磁浮交通的概念最早由美国人提出，1912年美国人埃米尔巴赫雷特就磁浮基本概念申请了美国专利。磁浮车与轨道非接触运行，具有无磨耗、噪声小、乘坐舒适度好等绿色环保特点，近年来得到迅速发展。根据列车悬浮方式不同，磁浮列车主要分为电磁悬浮(electromagnetic maglev suspension，EMS)、电动悬浮(electromagnetic dynamic suspension，EDS)和混合电磁悬浮(hybrid electromagnetic suspension,HES)三种基本类型。其中,EMS模式，尤其是中低速EMS模式，技术较为成熟，运营成本较低，非常适合城市交通的需求。

磁浮交通大多采用高架形式，车轨耦合振动现象是各类磁浮系统的共性问题，尤其是EMS磁浮系统，更存在此方面的问题。因为EMS型磁浮系统的悬浮额定间隙通常只有10 mm左右，电磁力和悬浮间隙之间的强非线性关系容易导致电磁力产生较大波动，进而引起车轨耦合振动问题。日本的HSST04车、德国的TR04车、美国的AMT系统、韩国的UTM-01列车都曾出现过车辆在桥梁轨道上发生剧烈的耦合振动现象[1]，国内某磁浮列车在道岔梁上也出现过因自激振动导致磁浮车辆无法正常运行的情况。为研究磁浮车轨耦合振动现象，国内外学者分别从磁浮车辆、控制器、轨道梁角度做了大量研究。文献[2]利用比列模型试验对车轨动力响应进行了分析。文献[3]基于现场试验，对轨道梁进行了动力响应测试。文献[4-7]建立了车轨耦合动力学模型，研究了常导磁浮列车的动态磁轨关系。文献[6]利用单铁系统仿真分析了电流环的响应特性，但并未从EMS磁浮系统整体考虑。

实际上，EMS磁浮列车在起浮阶段的悬浮间隙波动性更大，更易发生车轨耦合振动，而目前关于此方面的研究还很少，或仅限于单点悬浮系统下的仿真分析。鉴于此，本文建立了EMS中低速磁浮系统的“车辆-电磁-轨道梁”耦合动力学模型，对磁浮列车起浮阶段展开仿真试验，基于仿真试验对EMS磁浮系统起浮阶段的振动特性进行深入研究。

1 中低速磁浮系统耦合动力学模型

EMS中低速磁浮耦合动力学模型主要包括车辆模型、轨道模型和电磁控制模型，其中带有主动控制的电磁力模型是车轨耦合的纽带。

1.1 电磁控制模型

EMS中低速磁浮的电磁悬浮系统结构如图1所示。磁浮列车通过侧架下的电磁线圈实现车辆的悬浮，而每个侧架下方有四组线圈绕组磁铁，前后两个传感器分别控制两个电磁铁，直线电机提供牵引力，电磁铁和轨道间产生的电磁吸力提供悬浮力。

图1 悬浮系统结构Fig.1 Suspension system structure

图2 单点动力学模型Fig.2 Single pole dynamic model

电磁悬浮结构可简化为单点悬浮系统动力学模型，如图2所示[8]。文献[4]对电磁悬浮力的表达式进行了推导:

Fe=k(I/z)2

(1)

式中，Fe为电磁悬浮力;z为间隙变化量;I为线圈电流变化量;k为电磁力常数。

当考虑轨道梁柔性时，单点磁铁垂向动力学方程为

(2)

式中，m为悬浮电磁铁质量。

由电磁铁线圈输入电压和线圈电流关系得到

(3)

式中，U为输入电磁系统电压;R为电磁线圈电阻。

EMS型磁浮系统实际采用PD反馈控制结合加速度反馈控制系统，而文献[8]指出，由于电磁铁线圈的电感作用，线圈中的电流会有一定的延迟，也就是说，虽然控制算法可以根据传感器信号计算此刻所需的控制电流，但是由于电感作用，该电流要经过一段时间间隔才能真正作用到悬浮电磁铁上。因此，本文控制系统模型采取双环控制器(图3)。

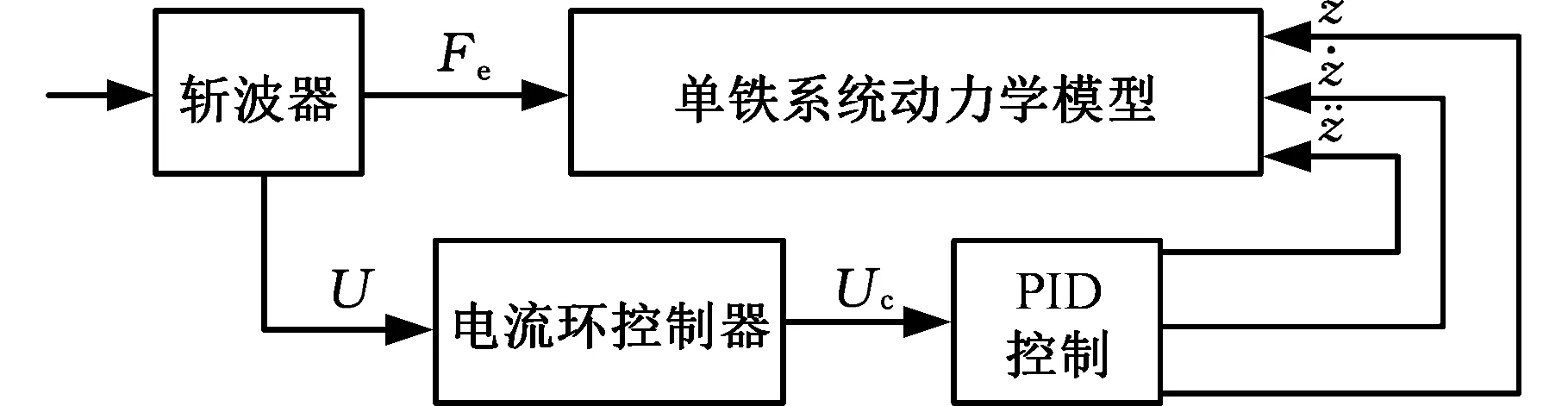
图3 控制系统基本结构Fig.3 Basic structure of control system

通过控制系统输入输出关系得到

U=kc10(Uc-kc20I)

(4)

(5)

(6)

式(6)对t求导可得

(7)

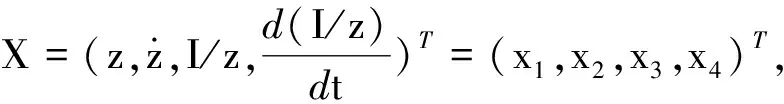
(8)

则受控的单点电磁铁悬浮系统模型[8]为

(9)

1.2 车辆动力学仿真模型

本文根据EMS中低速磁浮列车模型参数，建立磁浮列车动力学模型。单节磁浮车辆由5个悬浮模块组成，每个悬浮模块有左右两个悬浮侧架,每个悬浮侧架有6个自由度，悬浮侧架通过两组抗侧滚梁以及机械导向机构相连，每组抗侧滚梁间由垂向吊杆相连。每个悬浮侧架下有两个电磁悬浮控制模型，产生的电磁悬浮力作用于轨道梁上。车体由6组滑台支撑，每个滑台下方由空气弹簧支撑，空气弹簧安装在左右悬浮侧架上，每个悬浮侧架前后由两个空气弹簧支撑。为简化模型，对于机械导向机构只考虑其物理模型，整车均视为刚体，有6个自由度，滑台连接车体和空气弹簧，2位、5位滑台为固定滑台，自由度为0，其余8个滑台有一个横向自由度，左右悬浮侧架的电磁线圈简化为两组，一共20组电磁线圈，每个线圈6个自由度，因此，整车动力学模型共考虑194个自由度。车辆垂向结构如图4所示。EMS磁浮系统耦合动力学模型悬浮模块受力如图5所示。

图4 车辆垂向结构示意图Fig.4 Schematic diagram of vehicle structure

图5 悬浮模块受力图Fig.5 Suspension force diagram

悬浮模块垂向耦合运动微分方程为

(10)

式中，zf为悬浮模块垂向位移;g为重力加速度；Fe1、Fe2分别为第一悬浮点和第二悬浮点的电磁悬浮力;Mb为悬浮模块的质量；Fkcg1、Fkcg2分别为前后悬浮架抗侧滚梁施加给悬浮模块的垂向力；Fsp1、Fsp2分别为空气弹簧1、2施加的垂向力。

1.3 磁浮系统轨道梁有限元模型

根据文献[9]中提供的中低速磁浮道岔处钢制轨道梁结构参数,建立弹性轨道梁有限元模型如图6a所示。将经模态分析的轨道梁有限元模型导入Simpack中，得到柔性体模型如图6b所示。计算得到的一阶模态频率(图6c)和文献[10]中长沙中低速磁浮线路标准中给定的一阶模态频率(25 Hz)相近。由此说明本文建立的轨道梁模型较为准确。

根据模态叠加原理，轨道梁在载荷作用下的位移可由下式计算：

(11)

式中,Yn(x)为给定边界条件下的第n阶固有频率所对应的正则振型函数；qn(t)为未知的时间函数。

弹性轨道梁的受力如图7所示，其垂向运动方程如下：

(a)道岔主动梁有限元模型

(b)柔性体模型

(c)一阶模态频率图6 弹性轨道梁模型Fig.6 Flexible track beam model

图7 轨道梁受力图Fig.7 Track beam force diagram

(12)

(13)

式中，zb为轨道梁垂向位移；α为轨道梁绕y轴运动的夹角；Mt为轨道梁质量；It为轨道梁绕y轴的运动惯量；s为单点悬浮系统距离梁端的长度；l为轨道梁长度；Fv1、Fv2分别为轨道梁两端支座反力。

1.4 磁浮系统耦合动力学模型

基于Simpack建立 “车辆-电磁-轨道梁”系统耦合动力学仿真模型，图8为EMS磁浮系统车轨耦合系统示意图，可以看出，车轨耦合的关键是建立较为准确的电磁力模型，通过电磁力元实现轨道梁上节点和车辆动力学模型中悬浮架的连接，从而搭建车轨耦合动力学系统。车辆在起浮阶段的振动和轨道梁的自振通过电磁力元实现实时传递。

图8 车-轨耦合动力学模型基本结构Fig.8 Basic structure vehicle-rail couplingdynamics model

为了数值计算方便，基于式(9)在Simpack中建立电磁力控制模型。车-轨耦合动力学仿真模型如图9所示。

图9 车-轨耦合动力学仿真模型Fig.9 Vehicle-rail coupling dynamics simulation model

2 振动特性分析

为了研究车辆在弹性梁上的磁浮车辆的悬浮失稳现象，基于前文建立的车-轨耦合动力学系统模型，采用PD反馈控制方法[11]，在弹性轨道梁上对车辆起浮阶段进行分析。由于中低速磁浮车-轨耦合振动在垂向上较为剧烈，因此模型对横向结构做了相应简化。模型主要参数如表1所示。

表1 模型主要参数

图10 弹性轨道梁下位移响应Fig.10 Displacement response under elastic track beam

图10给出了车辆在弹性梁上起浮阶段轨道梁跨中位移和悬浮架垂向位移，可以看出，当车辆起浮后悬浮架的自激振动和弹性轨道梁的受迫振动较为剧烈，在3 s后悬浮架振动位移突然变为0附近的微幅振动，而此刻轨道梁的振动位移幅值达到最大，随后轨道梁振动幅值呈逐渐减小趋势。为进一步分析弹性梁上这一振动现象，图11给出了悬浮间隙和电磁力的变化情况。

图11 弹性轨道梁下悬浮间隙和电磁力变化Fig.11 Suspension gap and electromagnetic variation under elastic track beam

从图11中可以看出,悬浮间隙在3 s左右突变为0，电磁力在此刻变为无穷大。因为仿真初始时，给定初始静态悬浮间隙为9 mm，所以在第3 s时刻，由于悬浮架振动幅值过大，导致车辆悬浮间隙会变得较小，根据间隙和电磁力的关系，较小的悬浮间隙可能导致电磁力过大，产生的吸力使悬浮架上浮吸在轨道梁上。结合图10可解释3 s左右由于悬浮架发生了悬浮失稳，导致其上浮吸死在轨道梁上，因此出现了悬浮架位移的突变和轨道梁振动幅值先逐渐增大后减小的现象。

3 起浮阶段的车轨异常振动原因及措施分析

图12 弹性梁起浮阶段悬浮架频谱图Fig.12 Bode diagram of suspension frame in the lifting stage of flexible beam

图13 刚性梁起浮阶段悬浮架频谱图Fig.13 Bode diagram of suspension frame in the lifting stage of rigid beam

为研究弹性轨道梁上悬浮架和轨道梁产生剧烈耦合振动的原因，图12给出了起浮初始阶段悬浮架的振动频谱图。由图12可以看出，弹性梁条件下悬浮架振动幅值较大时，振动频率集中在了1 Hz附近及20～30 Hz区间内，而本文前述建立的轨道梁有限元模型，计算的其一阶垂向模态频率为25 Hz，因此，弹性梁的固有频率和悬浮架振动自激振动频率接近。根据车轨耦合振动特性[12],悬浮架和轨道梁发生剧烈耦合振动原因是悬浮架自激振动激发了轨道梁固有频率，使两者振动相耦合。由图13可以看出，刚性梁下振动幅值均较小，悬浮架在频率很低时，幅值略大，整个频域范围内没有发生较大的振动。

为证实这一说法，图14、图15对起浮阶段刚性梁和弹性梁上悬浮架和轨道梁位移响应结果进行了对比。研究刚性梁时，假设刚性梁无变形产生。 可以看出刚性梁下悬浮架的振动逐渐收敛，梁的位移响应也逐渐趋于稳定。证实了导致EMS磁浮车轨发生剧烈振动的主要因素是：质量较小的梁的固有频率易被悬浮架的自激振动激发，使悬浮架和轨道梁两者产生耦合振动。

图14 刚性梁和弹性梁下位移响应Fig.14 Displacement response under rigid and flexible beams

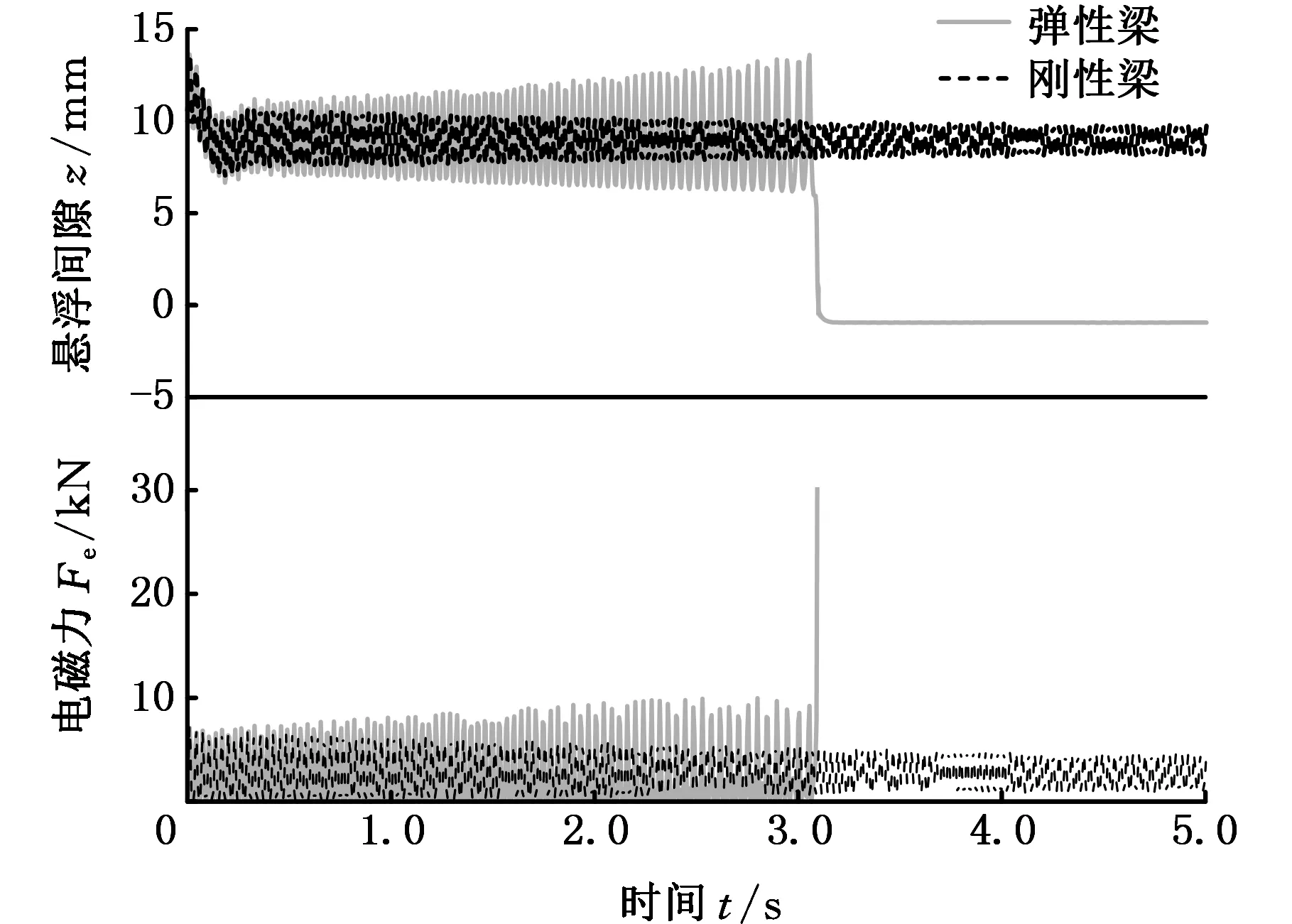
图15 刚性梁和弹性梁下电磁系统响应Fig.15 Electromagnetic system response under rigid and flexible beams

结合图14和图15可以看出，刚性梁也无法完全消除起浮阶段悬浮架和轨道梁的振动，悬浮架发生自激振动的原因是带有主动控制的电磁悬浮力发生变化。因此，从悬浮控制的角度分析，提高控制器的稳定性也可以缓解车轨耦合振动，图16、图17给出了刚性梁下双级悬浮控制器的振动响应和电磁系统的响应。

图16 不同控制器下的电磁系统响应Fig.16 Electromagnetic system response under different controllers

图17 不同控制器下的振动响应Fig.17 Vibration response under different controllers

从图16可以看出，起浮阶段单级悬浮控制器间隙波动较大，导致在单级悬浮控制器下车体加速度响应和梁跨中处位移响应也出现较大波动，且其收敛速度较慢。而双级悬浮控制器下悬浮间隙和电磁力很快趋于稳定。

4 结论

(1)EMS中低速磁浮列车在弹性轨道梁上起浮时，容易发生异常振动引起的悬浮失稳现象，其原因是单级悬浮控制模式的悬浮架自激振动频率激发了弹性轨道梁的固有频率，从而诱发了车轨剧烈耦合共振。

(2)为了缓解EMS中低速磁浮系统在起浮阶段的车轨耦合共振问题，提高轨道梁刚度或采用双级悬浮控制器模式是有效的方法。