两参数Birnbaum-Saunders疲劳寿命分布图像特征的拓展分析

徐晓岭，王蓉华，顾蓓青*

（1.上海对外经贸大学 统计与信息学院，上海201620；2.上海师范大学 数理学院，上海200234）

0 引 言

Birnbaum-Saunders模型是概率物理方法中一个重要的失效分布模型，由BIRNBAUM等[1]于1969年在研究主因裂纹扩展导致材料失效的过程中推导而来。此模型在机械产品可靠性研究中应用广泛，常用于疲劳失效研究；在电子产品性能退化失效分析中也有重要应用。

设T服从两参数Birnbaum-Saunders疲劳寿命分布BS(α,β)，分布函数F(t)与密度函数f(t)分别为：

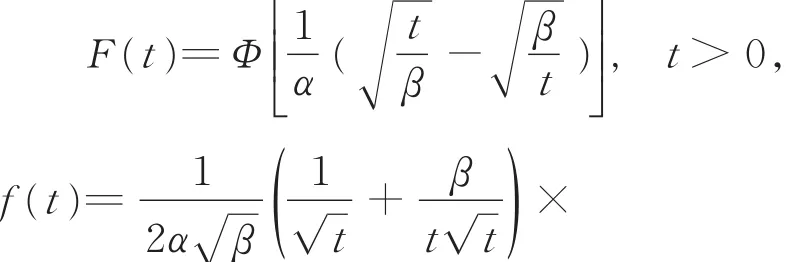
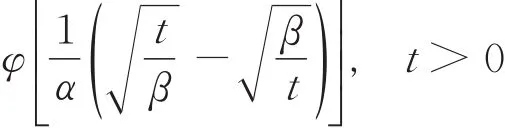
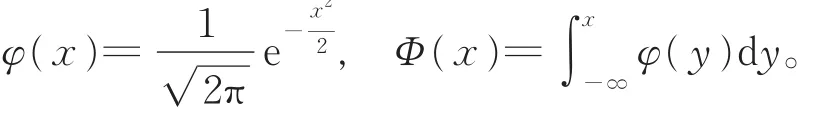
由于Birnbaum-Saunders疲劳寿命分布是基于疲劳过程的基本特征的，因此，较于常用的寿命分布，如威布尔分布、对数正态分布，更适合描述由疲劳引起失效的产品寿命规律。

关于两参数Birnbaum-Saunders疲劳寿命分布BS(α,β )的统计分析已有很多研究［1-29］。KUNDU等［14］证明了两参数BS分布的失效率函数的形状为“倒浴盆”形，同时，针对不同形状参数α，通过数值

其中，α＞0称为形状参数，β＞0称为刻度参数（或称为尺度参数），φ(x),Φ(x)分别为标准正态分布的密度函数与分布函数，即计算得到了失效率函数达到顶峰时的t值，称此点为变点（change point），记为 cα,β。cα,β的大小依赖于α的取值，变点可能分布在β的左右两侧。例如，当α=0.6 时 ，cα,β=2.536 4β；当 α=0.8 时 ，cα,β=0.992 3β；当 α=1时，cα,β=0.514 9β等。

1 BS（α，β）分布密度函数的图像特征

定理1设非负随机变量T～BS(α,β)，其分布函数和密度函数分别记为F(t)和f(t)，则f(t)的图像具有以下特征：

（1）f(t)在t∈(0,+∞)上“先严格单调上升后严格单调下降”，呈“倒浴盆”形；

（2）f(t)在t∈(0,β)上“先严格单调上升后严格单调下降”，呈“倒浴盆”形，而在 t∈ [β,+∞ )上“严格单调下降”。

证明由于β为刻度参数，不失一般性，设β=1，并记 ε(t)=-，则

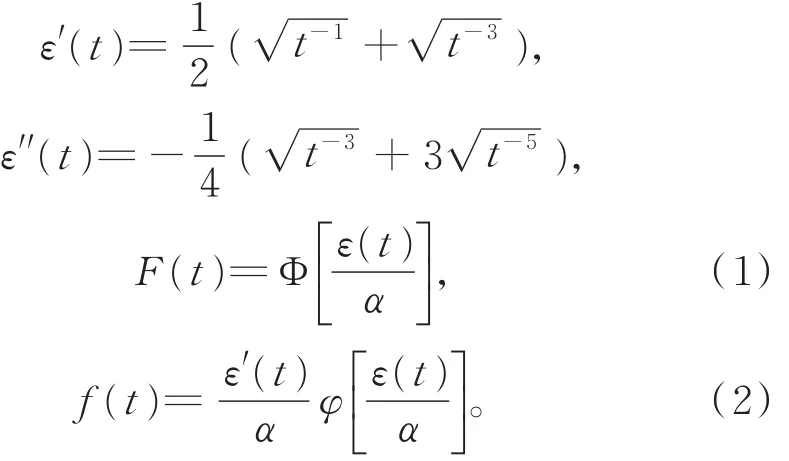
对t＞ 0，令函数

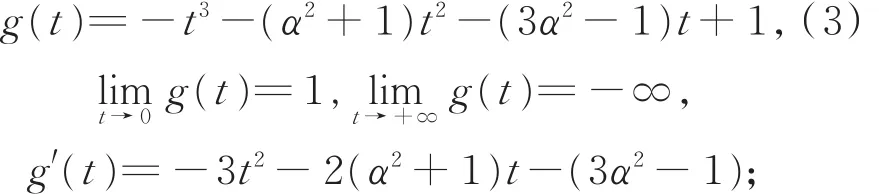
对t＞ 0，令函数

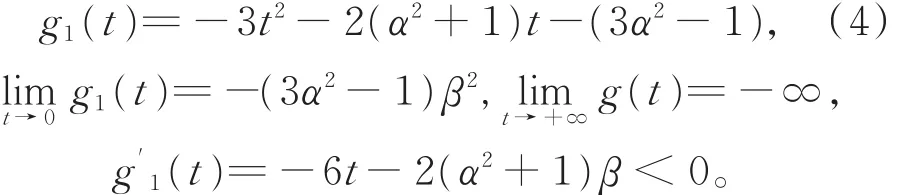
（ⅱ）类似于（ⅰ），对0＜ t＜ 1，令函数

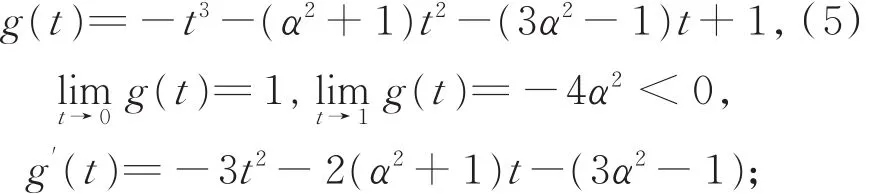
对0＜ t＜ 1，令函数

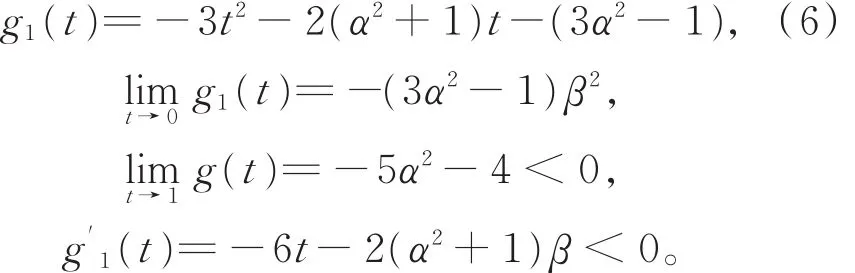
2 BS（α，β）分布失效率函数的图像特征

文献［14］主要利用了文献［30］的结论，证明失效率函数呈“倒浴盆”形。引理如下：

引理［30］设T为非负连续型随机变量，其密度函数f(t)存在二阶导数，记，有

（1）若 η′(t)＞ 0，即 η(t)是“严格单调增函数”，则λ(t)“严格单调上升”。

（2）若η′(t)＜ 0，即η(t)是“严格单调减函数”，则λ(t)“严格单调下降”。

（3）若存在 t0，t0＞ 0，η′(t0)=0，且 η(t)呈“先严格单调上升后严格单调下降”，即呈“倒浴盆”形，则λ(t)有可能呈“倒浴盆”形，也有可能“严格单调下降”。

（4）若存在 t0，t0＞ 0，η′(t0)=0，且 η(t)呈“先严格单调下降后严格单调上升”，即呈“浴盆”形，则λ(t)有可能呈“浴盆”形，也有可能“严格单调上升”。

用该引理考察对数正态分布失效率图像是十分有效的。值得注意的是，若η(t)本身形式复杂或单调性形式多样，则使用此引理有时并不能完全解决失效率函数的图像特征问题。

值得一提的是，在引理中要求“密度函数f(t)存在二阶导数”，其实，这一条件并不总能满足。下面例1和例2中的2个分布密度函数在t=β处二阶导数均不存在。

例1设非负随机变量T的分布函数F(t)为

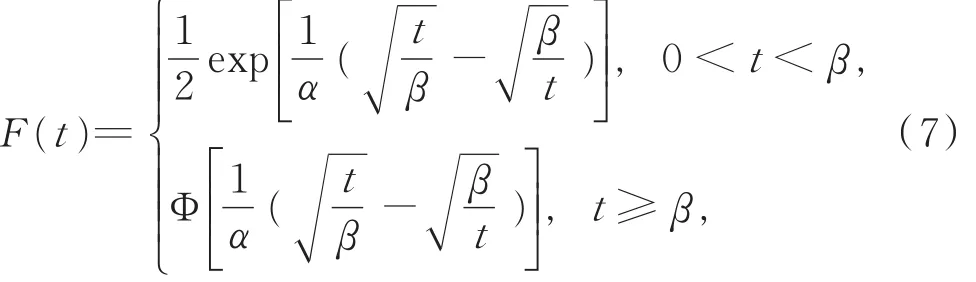
密度函数f（t）为

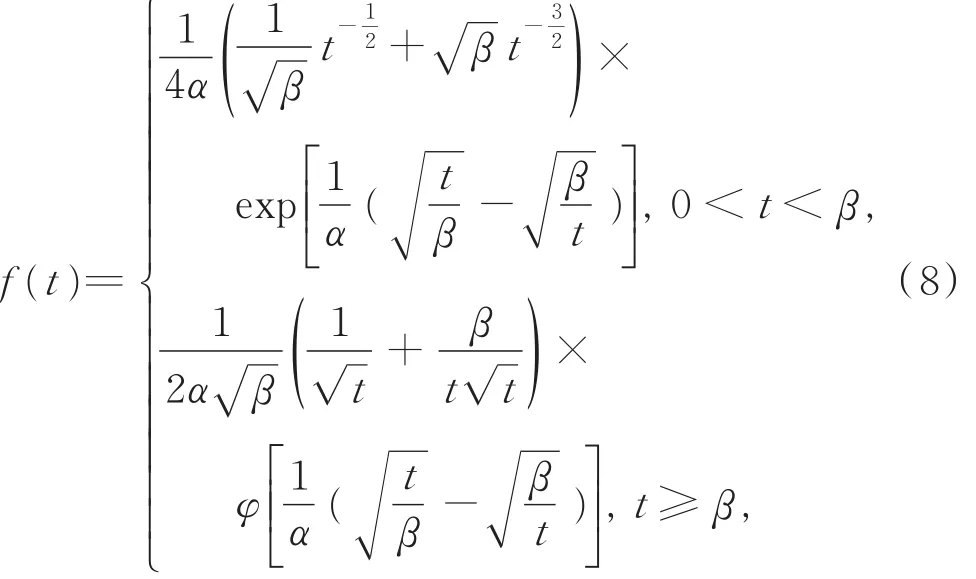
注意到

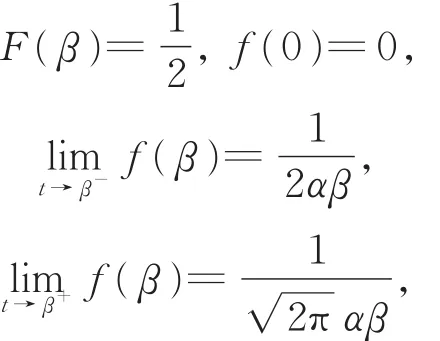
例2设非负随机变量T的分布函数F(t)为

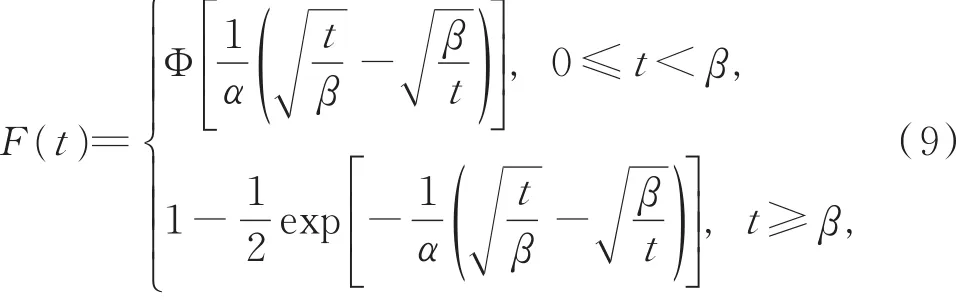
其密度函数为

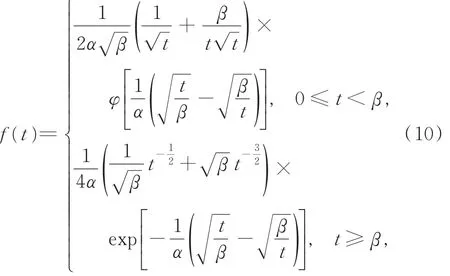
注意到

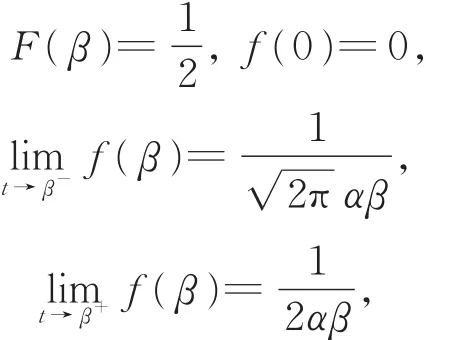
若在引理中，“密度函数f(t)存在二阶导数”这一条件不满足，那么，是否还有类似于引理的结论呢？定理2拓展了引理的结论，是判断失效率函数图像特征的更为一般的结论。

定理2设非负随机变量T的密度函数为，其分布函数F(t)、可靠度函数R(t)以及失效率函数λ(t)为：

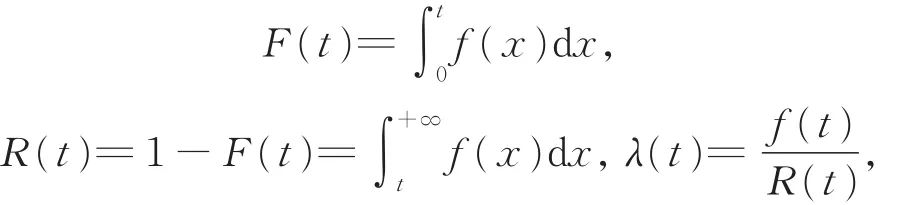
则有以下结论：

（Ⅰ）当0＜ t＜ a时，

（1）若 η′1(t)＞0，即 η1(t)是严格单调增函数，则λ(t)有可能“严格单调上升”，有可能“严格单调下降”，也有可能呈“倒浴盆”形。

（2）若 η′1(t)＜0，即 η1(t)是严格单调减函数，则λ(t)有可能“严格单调上升”，有可能“严格单调下降”，也有可能呈“浴盆”形。

（3）若 存在 t0，0＜ t0＜ a，η′1(t0)=0，且 η1(t)呈“先严格单调上升后严格单调下降”，即呈“倒浴盆”形，则λ(t)有可能“严格单调上升”，有可能“严格单调下降”，有可能呈“浴盆”形，有可能呈“倒浴盆”形，也有可能“先严格单调上升再严格单调下降而后再严格单调上升”。

（4）若 存在 t0，0＜ t0＜ a，η′1(t0)=0，且 η1(t)呈“先严格单调下降后严格单调上升”，即呈“浴盆”形，则λ(t)有可能“严格单调下降”，有可能“严格单调上升”，有可能呈“倒浴盆”形，有可能呈“浴盆”形，也有可能“先严格单调下降再严格单调上升而后再严格单调下降”。

（Ⅱ）当t≥ a时，

（1）若 η′2(t)＞0，即 η2(t)是严格单调增函数，则λ(t)“严格单调上升”。

（2）若 η′2(t)＜0，即 η2(t)是严格单调减函数，则λ(t)“严格单调下降”。

（3）若存在 t0，t0＞ a，η′2(t0)=0，且 η2(t)呈“先严格单调上升后严格单调下降”，即呈“倒浴盆”形，则λ(t)有可能呈“倒浴盆”形，也有可能“严格单调下降”。

（4）若存在 t0，t0＞ a，η′2(t0)=0，且 η2(t)呈“先严格单调下降后严格单调上升”，即呈“浴盆”形，则λ(t)有可能呈“浴盆”形，也有可能“严格单调上升”。

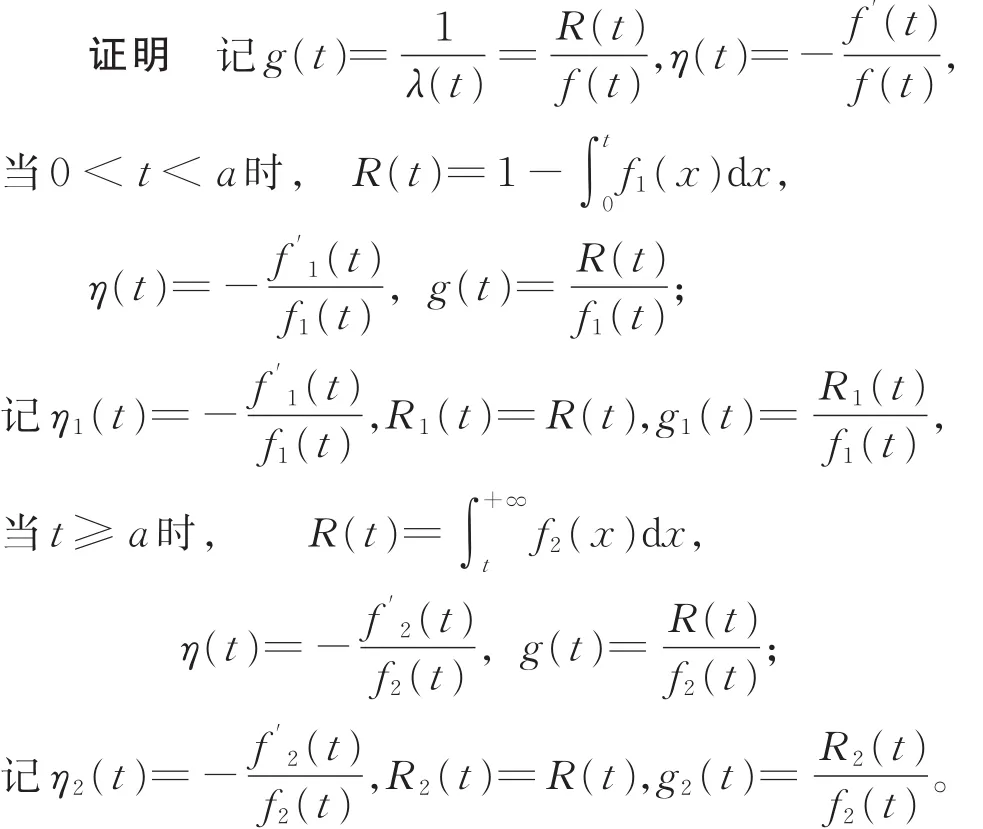
（Ⅰ）当0＜ t＜ a时，

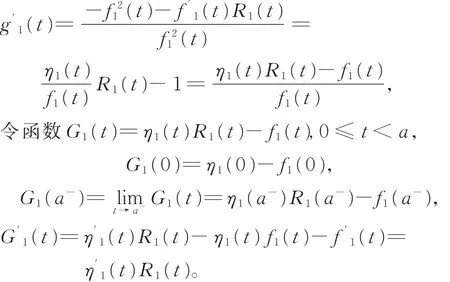
（ⅰ）若η′1(t)＞0，即η1(t)是严格单调增函数。此时有G′1(t)＞ 0，进而 G1(0)＜ G1(a-)。

（1）若 G1(a-)≤ 0，则 G1(t)＜ 0，g′1(t)＜ 0，进而λ(t)“严格单调上升”。

（2）若 G1(0)≥ 0，则 G1(t)＞ 0，g′1(t)＞ 0，进而λ(t)“严格单调下降”。

（3）存在 t0，0＜ t0＜ a，G1(t0)=0，当 0＜ t＜t0时，G1(t)＜ 0，g′1(t)＜0，λ(t)“严格单调上升”；当 t0＜ t＜ a时，G1(t)＞ 0，g′1(t)＞0，λ(t)“严格单调下降”。即λ(t)呈“倒浴盆”形。

（ⅱ）若η′1(t)＜ 0，即η1(t)是严格单调减函数。此时有G′1(t)＜ 0，进而 G1(0)＞ G1(a-)。

（1）若 G1(0)≤ 0，则 G1(t)＜ 0，g′1(t)＜ 0，进而λ(t)“严格单调上升”。

（2）若 G1(a-)≥ 0，则 G1(t)＞ 0，g′1(t)＞ 0，进而λ(t)“严格单调下降”。

（3）存在 t0，0＜ t0＜ a，G1(t0)=0，当 0＜ t＜t0时，G1(t)＞ 0，g′1(t)＞0，λ(t)“严格单调下降”；当 t0＜ t＜ a时，G1(t)＜ 0，g′1(t)＜0，λ(t)“严格单调上升”。即λ(t)呈“浴盆”形。

（ⅲ）若存在t0，0＜ t0＜ a，η′1(t0)=0，且 η1(t)呈“先严格单调上升后严格单调下降”，即呈“倒浴盆”形。当0＜ t＜ t0时，η′1(t)＞ 0，G′

1(t)＞ 0；当t＞ t0时，η′

1(t)＜ 0，G′1(t)＜ 0。（1）若 G1(t)≤ 0，则 g′1(t)≤0，进而λ(t)“严格单调上升”。

（2）若G1(t)≥ 0，则g′1(t)≥0，进而λ(t)“严格单调下降”。

（3）若 存 在 t1，t0＜ t1＜ a，G1(t1)=0，且 当0＜t＜t1时，G1(t)＞0，λ(t)“严格单调下降”；当t1＜t＜a时，G1(t)＜0，λ(t)“严格单调上升”。即λ(t)呈“浴盆”形。

（4）若 存 在 t1，0＜ t1＜ t0，G1(t1)=0，且 当0＜t＜t1时，G1(t)＜0，λ(t)“严格单调上升”；当t1＜t＜a时，G1(t)＞0，λ(t)“严格单调下降”。即λ(t)呈“倒浴盆”形。

（5）若 存 在 t1,t2，0＜t1＜t0＜t2＜a，G1(t1)=G1(t2)=0，且当 0 ＜ t＜ t1时，G1(t)＜ 0，λ(t)“严格单调上升”；当t1＜t＜t2时，G1(t)＞0，λ(t)“严格单调下降”；当t2＜t＜a时，G1(t)＜0，λ(t)“严格单调上升”。即λ(t)“先严格单调上升再严格单调下降而后再严格单调上升”。

（ⅳ）若存在t0，0＜ t0＜ a，η′1(t0)=0，且 η1(t)呈“先严格单调下降后严格单调上升”，即呈“浴盆”形 。 当 0＜t＜t0时 ，η′1(t)＜ 0，G′

1(t)＜ 0；当t＞ t0时，η′1(t)＞ 0，G′1(t)＞ 0。（1）若G1(t)≥ 0，则g′1(t)≥0，进而λ(t)“严格单调下降”。

（2）若 G1(t)≤ 0，则 g′1(t)≤0，进而λ(t)“严格单调上升”。

（3）若 存 在 t1，t0＜ t1＜ a，G1(t1)=0，且 当0＜t＜t1时，G1(t)＜0，λ(t)“严格单调上升”；当t1＜t＜a时，G1(t)＞0，λ(t)“严格单调下降”。即λ(t)呈“倒浴盆”形。

（4）若 存 在 t1，0＜ t1＜ t0，G1(t1)=0，且 当0＜t＜t1时，G1(t)＞0，λ(t)“严格单调下降”；当t1＜t＜a时，G1(t)＜0，λ(t)“严格单调上升”。即λ(t)呈“浴盆”形。

（5）若 存 在 t1,t2，0＜t1＜t0＜t2＜a，G1(t1)=G1(t2)=0，且当 0 ＜ t＜ t1时，G1(t)＞ 0，λ(t)“严格单调下降”；当t1＜t＜t2时，G1(t)＜0，λ(t)“严格单调上升”；当t2＜t＜a时，G1(t)＞0，λ(t)“严格单调下降”。即“λ(t)先严格单调下降再严格单调上升，而后再严格单调下降”。

（Ⅱ）当t≥ a时，

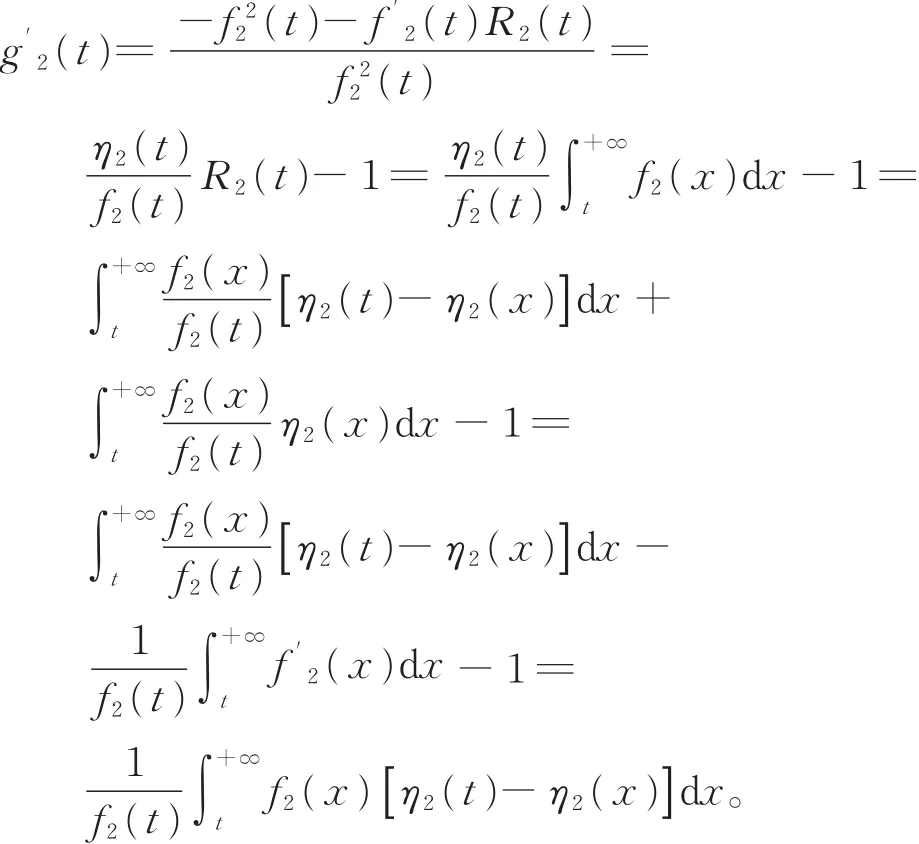
令函数

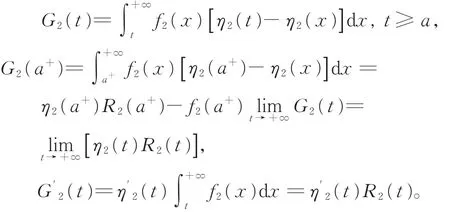
（1）若 η′2(t)＞0，即 η2(t)是严格单调增函数。对 x ≥ t时 ，有 η2(t)-η2(x)＜ 0，则 G2(t)＜ 0，g′(t)＜0，进而 λ(t“)严格单调上升”。2

（2）若 η′2(t)＜0，即 η2(t)是严格单调减函数。对 x ≥ t，有 η2(t)-η2(x)＞ 0，则 G2(t)＞ 0，g′(t)＞0，进而 λ(t“)严格单调下降”。2

（3）若存在 t0，t0＞ a，η′2(t0)=0，且 η2(t)呈“先严格单调上升后严格单调下降”，即呈“倒浴盆”形。而 G′2(t0)=0，当 a≤t＜t0时 ， η′2(t)＞ 0，(t)＞ 0；当 t＞ t0时，η′2(t)＜ 0，G′2(t)＜ 0。

（a）若 存 在 y0，y0＞ a，有 G2(y0)=0，则 有y0＜ t0。事实上，若反设y0≥ t0，

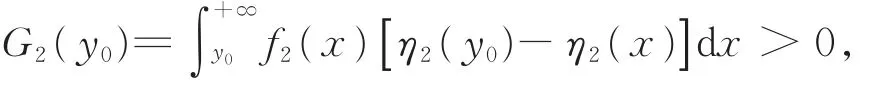
此与G2(y0)=0矛盾。

又由于G2(t)在t=t0处取最大值，而当a≤t＜ y0时，G2(t)＜ 0；当 y0＜ t＜ t0时，G2(t)＞ 0；当t＞ t0时，

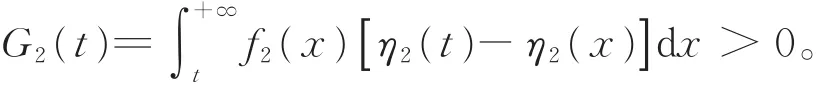
于是，当 a ≤ t＜ y0时，G2(t)＜ 0，g′2(t)＜ 0，进而λ(t“)严 格 单 调 上 升 ”；当t＞y0时 ，G2(t)＞0，g′(t)＞0，进而 λ(t“)严格单调下降”。即 λ(t)呈2“先严格单调上升后严格单调下降”，亦即呈“倒浴盆”形。

（b）若不存在 y0，y0＞ a，使 G2(y0)=0成立。则 对 t≥ a，有 G2(t)＞ 0 或 者 G2(t)＜ 0。 又 当t＞ t0时，

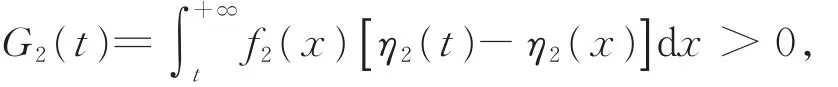
由此可知，只能有G2(t)＞0。进而g′2(t)＞ 0，即λ(t“)严格单调下降”。

（4）若存在 t0，t0＞ a，η′2(t0)=0，且 η2(t)呈“先严格单调下降后严格单调上升”，即呈“浴盆”形。而G′2(t0)=0，当 a ≤ t＜ t0时，η′2(t)＜ 0，G′2(t)＜ 0；当t＞ t0时，η′2(t)＞ 0，G′2(t)＞ 0。

（a）若 存 在 y0，y0＞ a，有 G2(y0)=0，则 有y0＜ t0。事实上，若反设y0≥ t0，

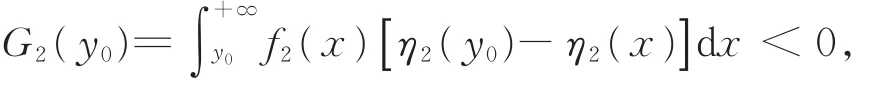
此与G2(y0)=0矛盾。

又由于G2(t)在t=t0处取最小值，而当a≤t＜ y0时，G2(t)＞ 0；当 y0＜ t＜ t0时，G2(t)＜ 0；当t＞ t0时，

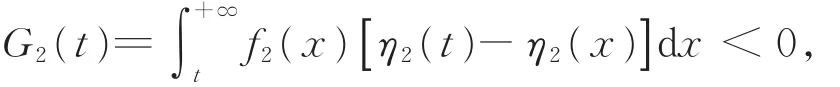
于是当a ≤ t＜ y0时，G2(t)＞ 0，g′2(t)＞ 0，进而λ(t“)严 格 单 调 下 降 ”；当t＞y0时 ，G2(t)＜0，g′(t)＜0，进而 λ(t“)严格单调上升”。即 λ(t)呈2“先严格单调下降后严格单调上升”，亦即呈“浴盆”形。

（b）若不存在 y0，y0＞ a，使 G2(y0)=0成立。则 对 t≥ a，有 G2(t)＞ 0 或 者 G2(t)＜ 0。 又 当t＞ t0时，

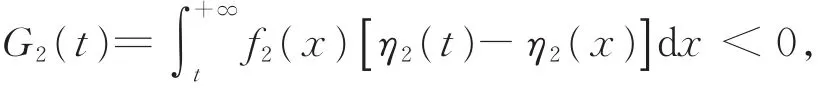
由此可知，只能有G2(t)＜0。进而g′2(t)＜ 0，即λ(t“)严格单调上升”。

注1如在定理2中令a=0，则可得到引理的结论。

注2在判断失效率函数λ（t）是否呈“浴盆”或“倒浴盆”形时，通常可先通过判断λ（t）=0是否成立，如成立，则排除了λ（t）严格单调上升（或下降）这一情形。

定理3给出了BS(α,β )的失效率函数 λ(t)更为清晰的图像特征。

定理3设非负随机变量T～BS(α,β)，其分布函数、密度函数和失效率函数分别记为F(t)、f(t)和λ(t)，则λ(t)的图像具有以下特征：

（Ⅰ）λ(t)在t∈(0,+∞)上“先严格单调上升后严格单调下降”，呈“倒浴盆”形。

（Ⅱ）当α2≤时，λ(t)在 t∈ (0,β)上“严格单调上升”；当 α2＞时，λ(t)在 t∈ (0,β)上“先严格单调上升后严格单调下降”，呈“倒浴盆”形。

（Ⅲ）当 α2＜时，λ(t)在 t∈[β,+∞)上“先严格单调上升后严格单调下降”，呈“倒浴盆”形；当α2≥时 ，λ(t)在 t∈[β,+∞)上“ 严 格 单 调下降”。

（Ⅳ）当 α2=时，λ(t)在t= β处取极大值，即当0＜t＜ β时，λ(t“)严格单调上升”；当t＞ β时，λ(t)“严格单调下降”。

证明易见失效率函数为

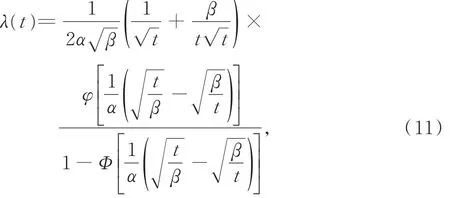
由于β为刻度参数，不失一般性，设β=1，并记ε(t)=-，则

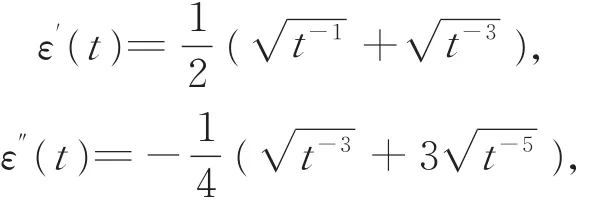
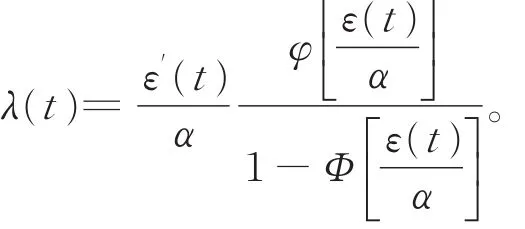
（Ⅰ）关于λ(t)在t∈(0,+∞)上呈“倒浴盆”形，这一结论可由文献［14］直接得到，另外

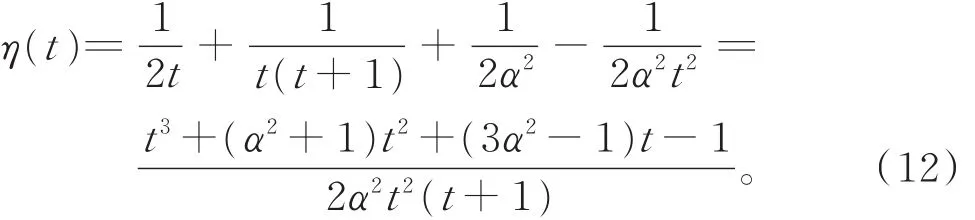
（Ⅱ）当0＜ t＜ 1时，

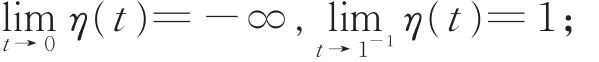
对0＜ t＜ 1，令函数

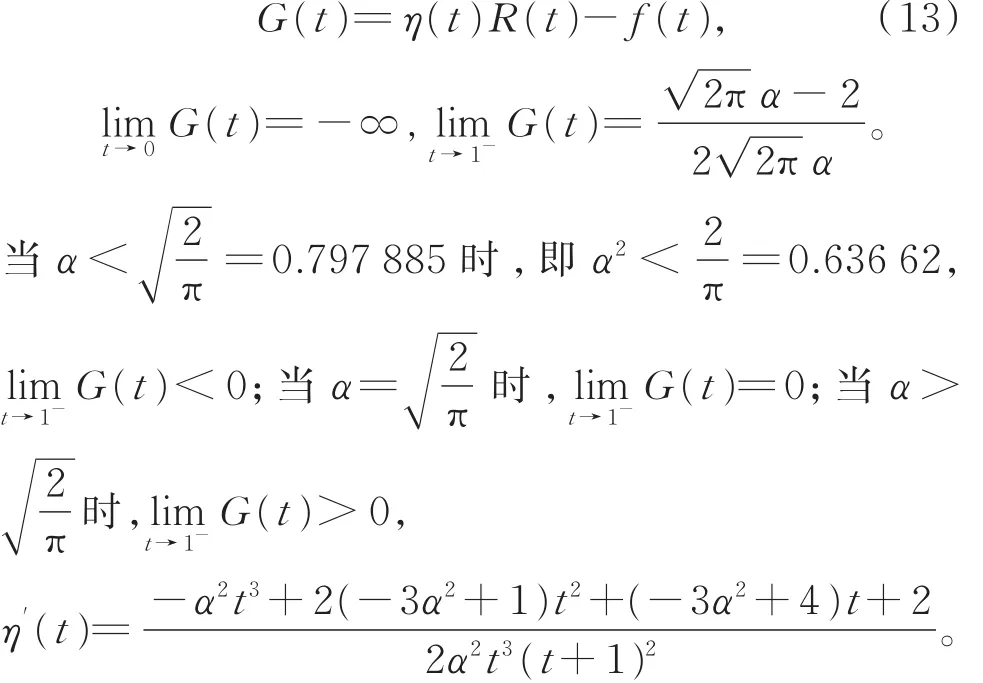
对0＜ t＜ 1，令函数

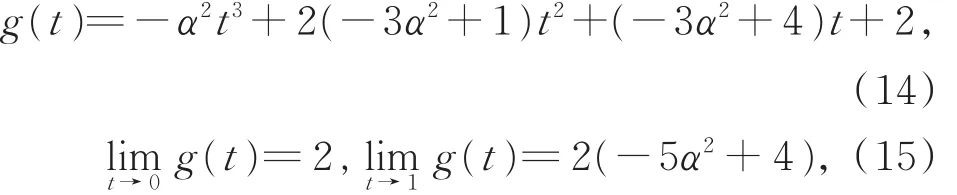
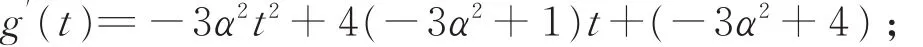
对0＜ t＜ 1，令函数

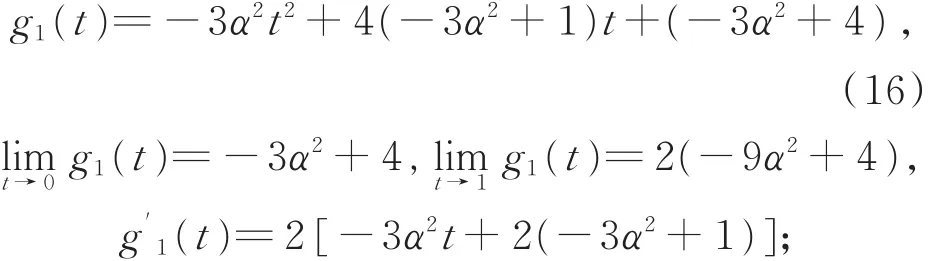
对0＜ t＜ 1，令函数

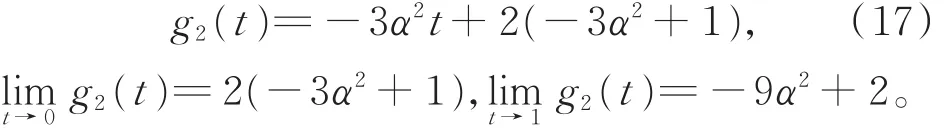
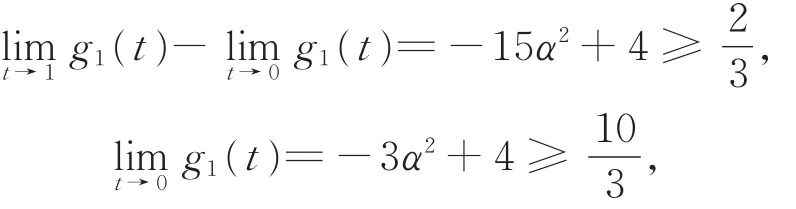
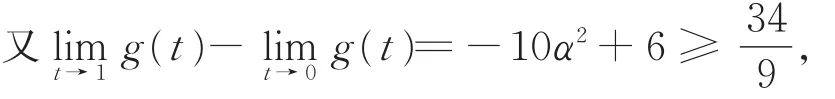
则 g1(t)＞ 0，g′(t)＞ 0。则 g(t)＞ 0，η′(t)＞ 0，且G(t)＜ 0，于是 λ(t)在t∈(0,1)上“严格单调上升”。

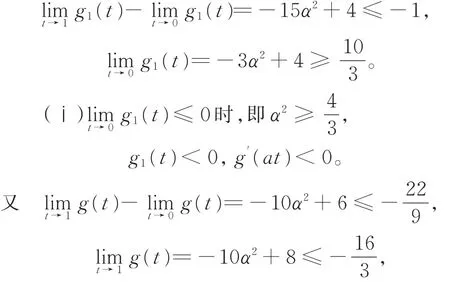
则存在 t0,0＜ t0＜ 1，有 g(t0)=0，当 0＜ t＜ t0时 ，g(t)＞ 0，η′(t)＞ 0，G′(t)＞ 0；当 t0＜ t＜ 1时，g(t)＜ 0，η′(t)＜ 0，G′(t)＜ 0。

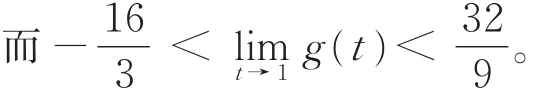
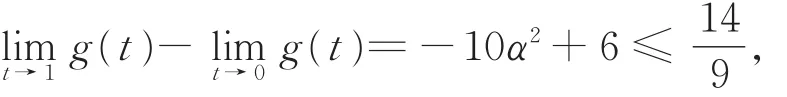
g(t)＞ 0，η′(t)＞ 0，而G(t)＜ 0，则 λ(t)在t∈(0,1)上“严格单调上升”。

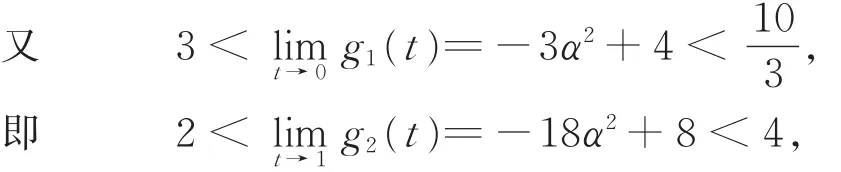
则 g1(t)＞ 0，g′(t)＞ 0。即

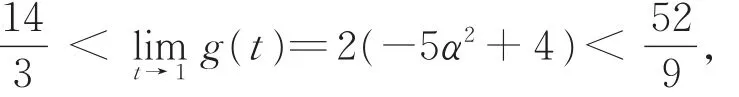
进 而 g(t)＞ 0，η′(t)＞ 0，又G(t)＜ 0，则 λ(t)在t∈(0,1)上“严格单调上升”。

（Ⅲ）当t≥ 1时，

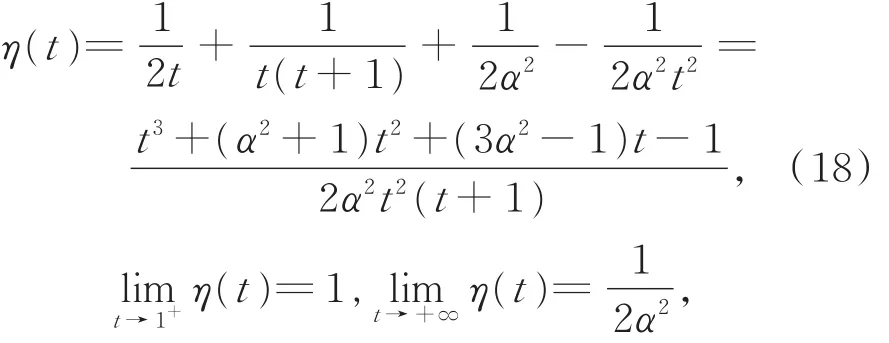
对t≥ 1，令函数

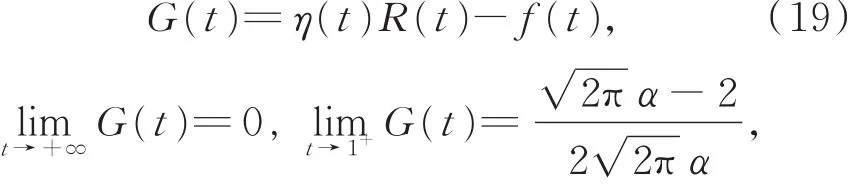
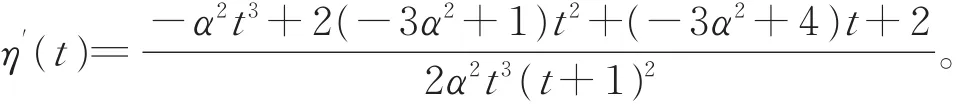
对t≥ 1，令函数

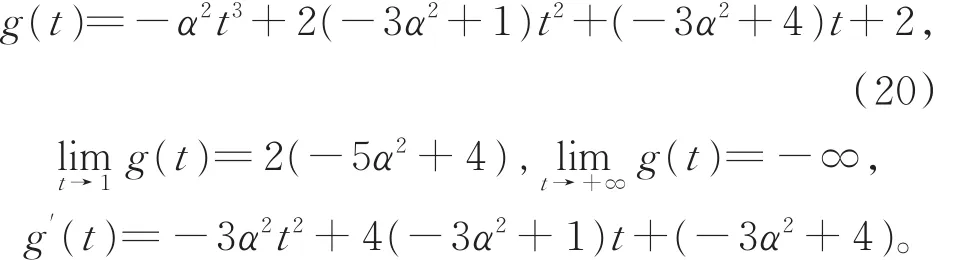
对t≥ 1，令函数

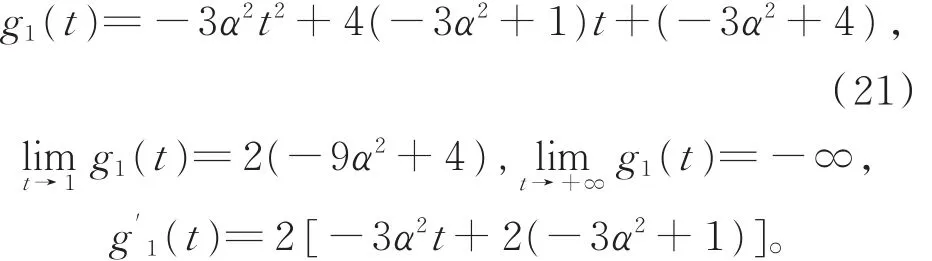
对t≥ 1，令函数

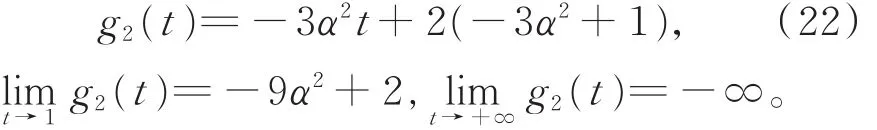
（a）当 α2＜G(t)＜ 0，此 时≤，存在 t*0，1≤ t*0＜ t0，G(t*0)=0，且当 1≤t＜t*0时，G(t)＜0，λ(t)“严格单调上升”；当t＞t*0时，G(t)＞0，λ(t)“严格单调下降”。即λ(t)在t∈[1,+∞)上呈“倒浴盆”形。

（b）当 α2≥G(t)＞ 0，此 时，易见G(t)＞0，λ(t)在t∈[1,+∞)“严格单调下降”。

综上可知，当 α2＜时，λ(t)在 t∈[1,+∞)上呈“倒浴盆”形；当α2≥时，λ(t)在t∈[1,+∞)上“严格单调下降”。

（Ⅳ）易见，当α2=时，λ(t)在t=1处取极大值，即当0＜t＜1时，λ(t“)严格单调上升”；当t＞1时，λ(t“)严格单调下降”。

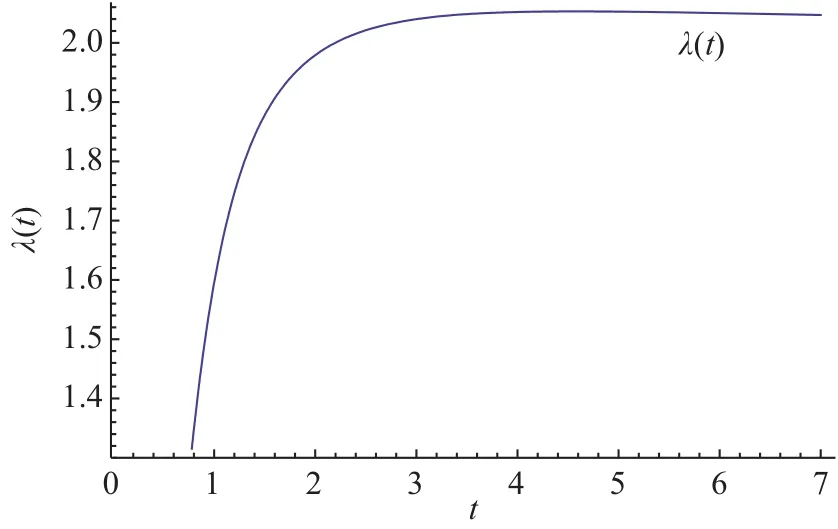
图1 α=0.5，β=1Fig.1 α=0.5，β=1

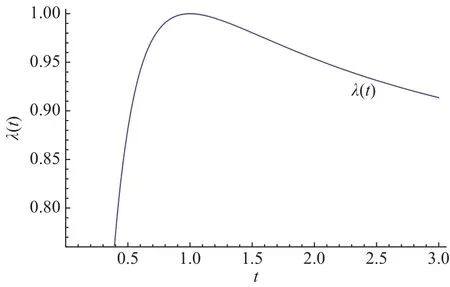
图2 α=，β=1Fig.2 α=，β=1

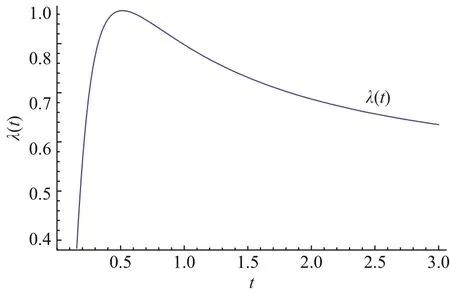
图3 α=1，β=1Fig.3 α=1，β=1

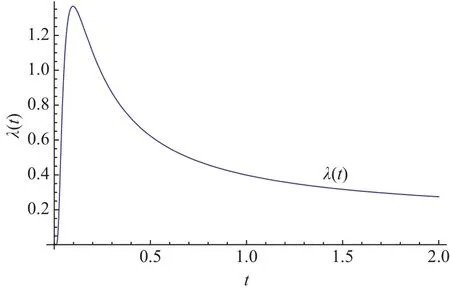
图4 α=2，β=1Fig.4 α=2，β=1